「MPC-Mike Rosulek 」:Overview of Secure Computation and Yao's Protocol
本系列是总结Mike Rosulek教授在上海期智研究院的密码学学术讲座。
这是Mike教授的第一个分享:Overview of Secure Computation and Yao’s Protocol
Roadmap
- Secure computation: Concepts & definitions
- Yao’s protocol: semi-honest secure computation for boolean circuits
主要内容包括安全多方计算的整体介绍及其应用场景、如何定义安全多方计算的security、Yao的混淆电路协议 (garbled circuits protocol)。
(咕咕咕博客选手回来了,学长说:与其担心有没有学读,不如多学学密码学,泪目,我觉得他说的对!)
Secure computation
Concepts
什么是安全计算?
Mutually distrusting parties, each with a private input.
【参与方之间互不信任,且都有一个隐私输入】
Learn the result of agreed-upon computation.
【参与方希望能得到一个各方商定的计算结果】
安全计算能保证什么?
Privacy (“learn no more than” prescribed output)
【隐私性:参与方除了得到商定的计算结果,其他都不能得到】
Input independence
【各参与方的输入无关】
Output consistency
【各参与方的输出是一个商定一致的计算结果】
以上性质及时在某些参与方勾结欺骗的情况下,也是成立的。

scenarios
Example 1: Sugar Beets——甜菜定价

Farmers make bids (“at price X, I will produce Y amount”)
【Farmers:会根据甜菜的定价决定产量,价格对产量的影响如上图蓝色的线】
Purchaser bids (“at price X, I will buy Y amount”)
【Purchaser:会根据甜菜的定价觉得购买量,价格对购买量的影响如上图红色的线】
Market clearing price (MCP): price at which total supply = demand
【双方希望甜菜价格能达到市场出清价,即产量=需求量】
但是双方不希望透露自己心中的定价,因为这会破坏经济市场的balabala
因此,在2009年,通过双方可以通过安全计算得到市场出请价。
Example 2: Ad conversion——广告投放

特斯拉存储了到店购买汽车的用户邮箱,而谷歌希望能个性化的投放汽车广告。
因此,如果双方公开数据库中的数据,就可以通过上图的SQL语句筛选出目标用户。
但这样会侵犯用户的用户的隐私,所以特斯拉和谷歌都不会直接公开用户的信息。由此,双方可以通过安全计算得到广告投放的目标用户。
Example 3: Wage Equity Study——薪资公平性研究

研究人员想研究Boston的薪资水平是否是性别平等的,但各企业不会愿意直接公开薪资。
而通过安全计算,可以在保护企业薪资隐私的情况下,得到相关研究结果。
Definitions
“securely” compute f ?
如何理解“安全地“计算f?
可以先从安全性需求/威胁来理解什么是不安全。
What if adversary learns more than f(x, y)?
【如果攻击者学到了除商定计算结果f(x,y)以外的信息?】
What if adversary learns f(x, y) but then prevents honest party from learning it too?
【如果攻击者能够得到计算结果,但是阻碍诚信的参与方得到正确的计算结果?】
What if adversary forces several parties to have inconsistent outputs?
【如果攻击者通过某种手段使得一些参与方得到不一致的计算结果】
What if adversary’s choice of input depends on honest party’s input?
【如果攻击者的输入会依赖一些诚信参与方的输入?】(不太理解这是一个什么样的情况?)
Security in ideal world
在理想情况下,假设有一个可信第三方,Alice和Bob把自己的输入x, y 告诉她,可信第三方计算f(x, y) ,再把计算结果分别分发给Alice和Bob。
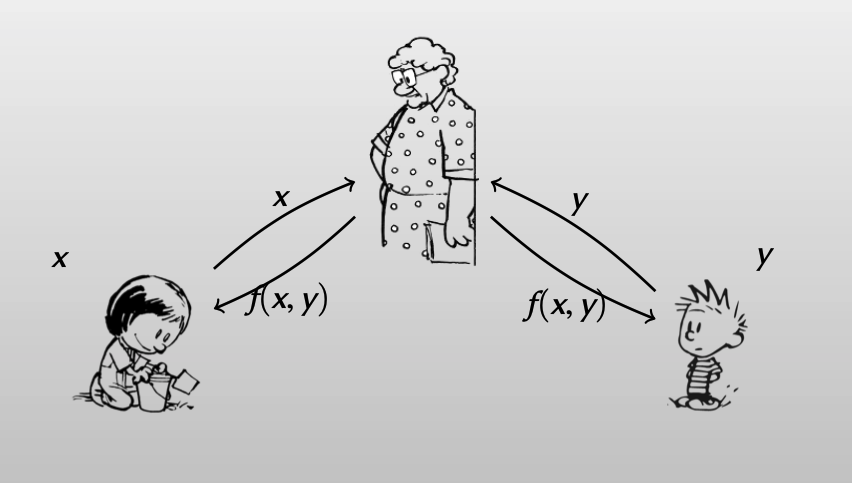
在理想情况中,如果有一个恶意的参与方,结果会怎么样?(你看图,变坏的人变丑了2333
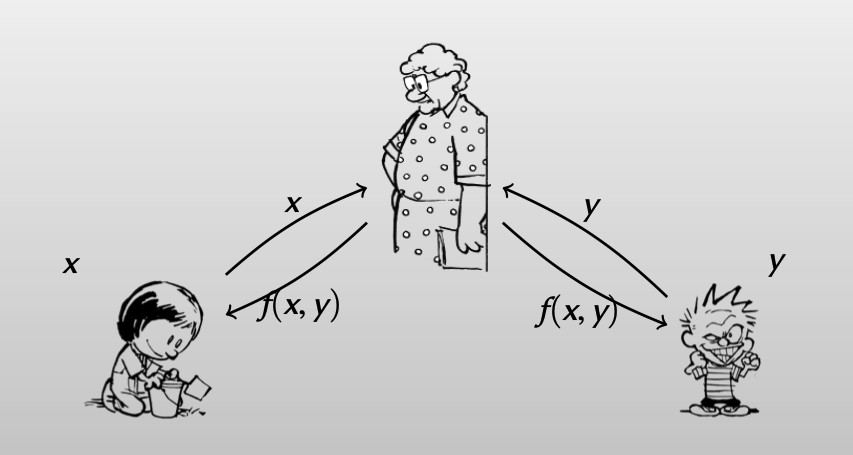
corrupt party’s view:
- 随意选择一个输入y
- 除了知道
f(x, y),其他信息都不知道。 - 致使诚信参与方得到一致的
f(x, y)
可见,在理想情况下,即使有恶意的参与方,也能达到之前提到的“安全地”计算f(x, y) 的要求。
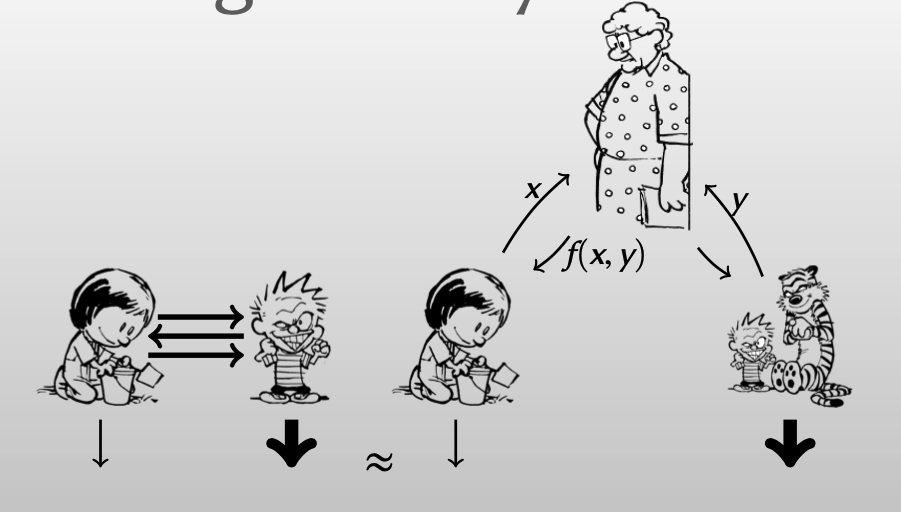
Security goal: real protocol interaction is as secure as the ideal-world interaction
For every “attack” against real protocol, there is a way to achieve “same effect” in ideal world
【因此,现实情况的安全计算目标应该是达到和理想情况中的同等安全性。】
【对于每一个尝试攻击真实安全计算协议的攻击者来说,总有一种方式达到 和攻击理想情况的 相同影响。】
首先,先解释在real protocol中,恶意参与方会产生什么样的effect?
下图是一个现实的MPC协议交互图(有恶意参与方):
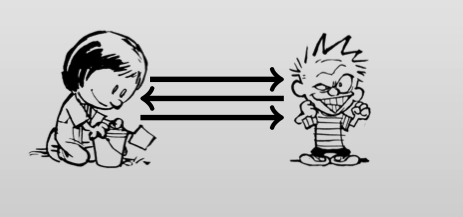
effect:
Something the adversary learns / can compute about honest party
【恶意参与方通过MPC得到的计算结果,可能能计算一些关于可信参与方的信息】
Some influence on honest party’s output
【恶意参与方能够影响可信参与方得到的计算结果】
Defining security
完整的安全定义: RanCanetti13
Universally Composable Security: A New Paradigm for Cryptographic Protocols
Security definition: For every real-world adversary $\mathcal{A}$, there exists an ideal adversary $\mathcal{A’}$ s.t. joint distribution (HonestOutput,AdvOutput) is indistinguishable.
【对于每一个真实协议交互下的攻击者 $\mathcal{A}$ ,都存在一个在理论协议情况下的攻击者 $\mathcal{A’}$ ,这两个攻击者产生的effect是相同的,两种情况下的诚信参与方的输出和恶意参与方的输出的 联合分布 是不可区分的。】
现在,来解释如何产生上文提到的:For every “attack” against real protocol, there is a way to achieve “same effect” in ideal world.
假设在理想情况中有一个simulator:simulates real-world interaction in ideal world
【可以在理想情况中模拟现实协议的交互。】
对于该模拟器来说,他可以扮演两种角色:
Send protocol messages that look like they came from honest party
- Demonstrates that honest party’s messages leak no more than f(x, y)
【和恶意参与方交互,模拟现实协议中的诚信参与方:对模拟器来说,他除了知道计算结果
f(x, y)外】Extract an f-input by examining adversary’s protocol messages
- “Explains” the effect on honest party’s output in terms of ideal world
【在理想协议中,模拟器提取来自恶意参与方的输入信息,模拟理想情况中的参与方。】
Q: yuyu老师问,这里的extract是什么意思?
A:在现实安全计算的协议交互中,不管恶意参与方提交什么输入,总能商定一个结果。因此在理想情况中,也许恶意参与方只是上传了一些garbage bit,模拟器需要从这些garbage bits中提取一些信息,作为参与交互的输入。
Semi- Honest security
有一种特殊的情况,即攻击者是semi-honest:
Adversary assumed to follow the protocol on a given input
【攻击者在给定输入下遵守协议】
Adversary may try to learn information based on what it sees
【但攻击者会尝试从得到的信息中学到一些其他信息】
No need to extract, only simulate transcript given ideal input+output
【因为攻击者会遵守协议,所以模拟器不需要extract来自半诚实的攻击者,只需要传送来自半诚实参与方的输入和可信第三方的计算输出结果。】
Yao’s protocol
Yao’s protocol : semi-honest secure computation for boolean circuits.
warm-up protocol: garbled truth table
Alice方:会计算一个混淆真值表(garbled truth table)
Write truth table of function f
【写下函数f的真值表,该函数对于Alice方有4种输入,对Bob方有4种输入】

For each possible input, choose random cryptographic key
【对于函数的每一种输入,Alice都选择一个随机的密钥(也叫label),对于Alice方的输入有4种密钥,对于Bob方的输入有4种密钥。】

Encrypt each output with corresponding keys
【再用对应的输入密钥加密每一个函数的输出】

Randomly permute ciphertexts, send to Bob
【对第三步的加密真值表随机置换,得到garbled truth table,再发给Bob。】

而对于Bob方:(先不考虑如何得到正确的密钥Ax和By)Bob得到了密钥Ax和By,对garbled truth table进行尝试性解密,就只能得到f(x, y)
对于Bob来说,是通过OT来得到正确的密钥Ax和By。后面会解释OT的简易版本和更为常用的做法。
Q:Bob如何判断这是正确的解密?
A:在对字符加密前,可以对字符加一些标记,比如前导0,或者特殊字符串之类。
在Bob收到garbled truth table和garbled input后,Bob的视角可以模拟成下图:

并且,对于distinguisher来说,只要密钥{A, B}中有一个不知道,那么 $\mathbb{E}{A, B}(C)\approx \mathbb{E}{A’, B’}(C’)$ ,(即和其他不知道的输入的加密是不可区分的)这样的模拟就是不可区分的。
Extending warm-up protocol
但这样的协议还存在一些问题:
Problem: Cost scales with the truth table size of f
【对于复杂函数来说,真值表的大小会很大,计算开销和存储开销都会很大】
How does Bob magically learn “correct” Ax, By?
【之前忽略的假设,Bob如何才能得到Alice制定的密钥Ax和By】
这里会先解决第一个问题,想法是把这个复杂函数拆分成多个garbled truth table,可以用一个garbled table 的garbled outputs作为另一个garbled table的keys,就像这样:
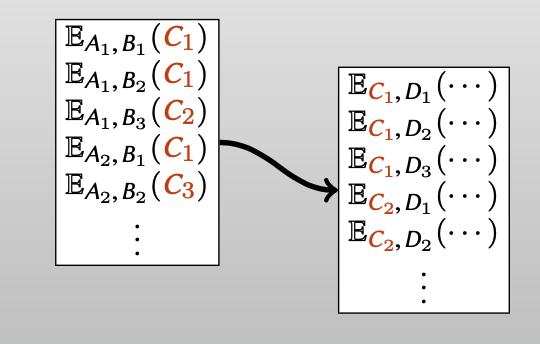
第二个问题,关于OT的部分,后文会继续解释。
Garbled circuit framework
对于garbled circuit framework的提出,出自姚期智院士86年的论文。
用boolean电路表示一个函数,电路由一些门组成:
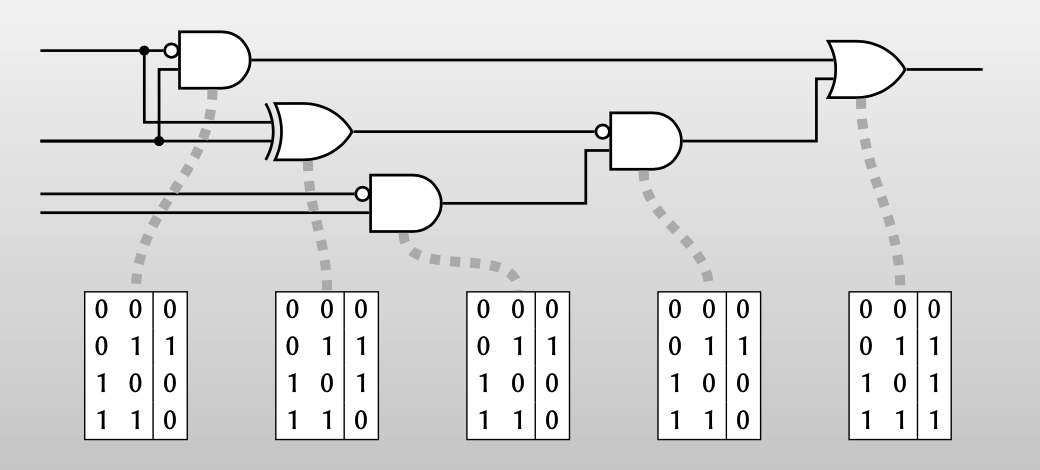
(Alice) Garbling a circuit:
Pick random labels W0, W1 on each wire
【对于每一个wire,都会选择两个label来表示true和false,比如选择A0是true,A1是false,这里的label其实就是上文提到的加密密钥。】
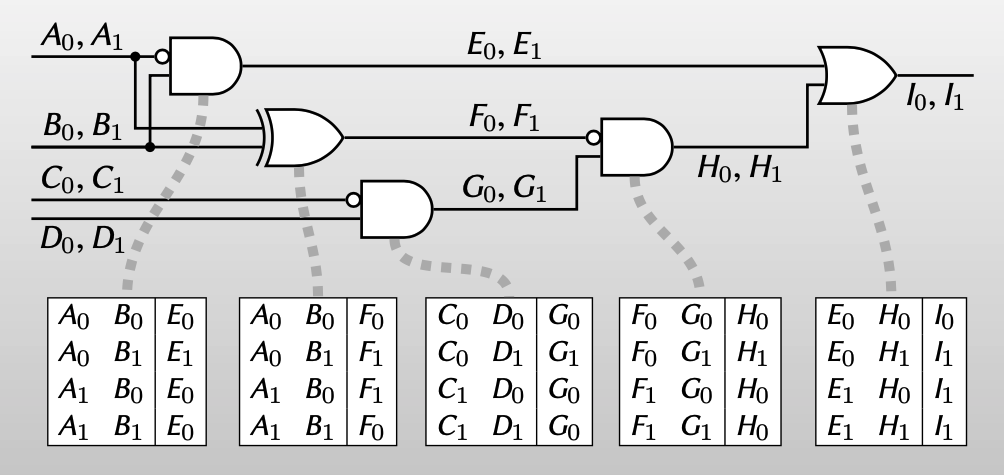
“Encrypt” truth table of each gate
【然后,对每一个门,都用对应的label加密真值表】
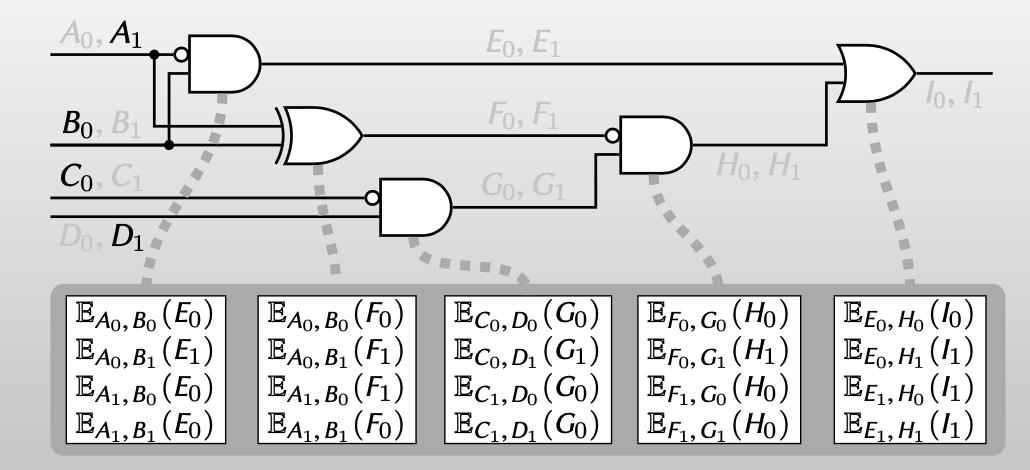
Garbled circuit = all encrypted gates
Garbled encoding = one label per wire
【这样就把一个混淆电路变成一些加密真值表,同样的,把混淆电路的编码变成了每个wire的一个label】
(Bob) Garbled evaluation:
Bob收到了混淆电路(garbled circuit)和混淆输入(garbled input),就可以进行garbled evaluation
Only one ciphertext per gate is decryptable
【对于Bob来说,他只有输入wire的单个label,因此对于每一个门,他都只能解密加密真值表中的一项】
Result of decryption = value on outgoing wire
【输出门的值就是最后的计算结果】
对于接受方Bob来说,它的任务就是用garbled input来evaluate garbled circuits。他只能学习到每个wire的一个label,计算上不可能的去猜测这个wire的另一个label是什么。而对于输出门的输出wire,即使揭露输出wire的两个label也只会泄漏电路的输出。
在BellareHoangRogaway12中有对gabled circuit做一些正式的符号定义:
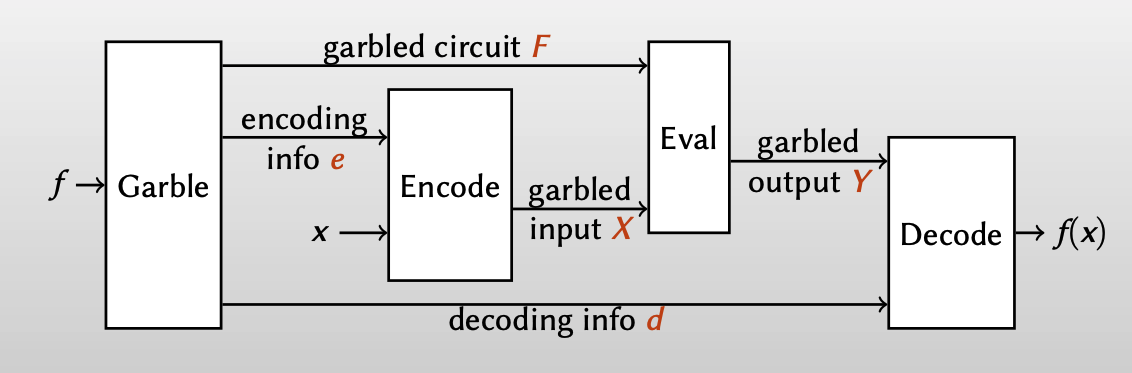
Privacy: (F,X,d) reveals nothing beyond f and f(x)
Obliviousness: (F,X) reveals nothing beyond f
Authenticity: given (F, X), hard to find Y‘ that decodes $\notin$ {f(x), ⊥}
Oblivious transfer
回到之前说的第二个问题,对于evaluator,也就是Bob,如何才能得到garbled circuit的garbled input?
对于下图的garbled circuit,需要Alice输入A和B,需要Bob输入C和D。
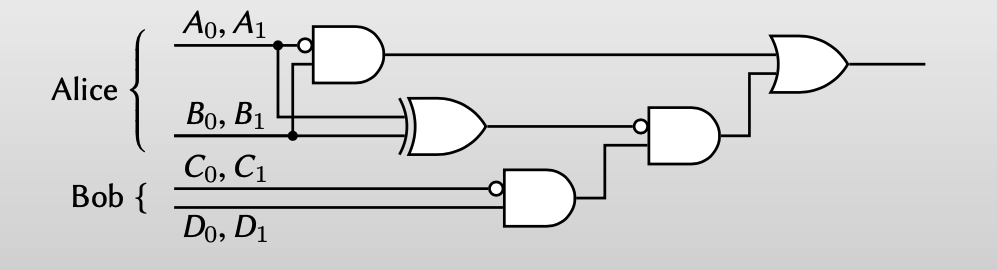
Garbler’s input: Alice 作为garbler,她知道每个wire的两个label(比如A0, A1),也知道label对应的真值关系(比如A0是false,A1是true),那Alice只需要把她的输入的对应的那个label发送给Bob就好了。
Evaluator’s input: 我们需要用OT(oblivious transfer)来实现,让Bob从Alice手中获得他想要的label,但又不让Alice知道他想要的是哪一个label。
如何构造不经意传输(OT)?
下图是一种简单实现的OT,不是最优的协议,后面的文章会继续介绍常用的OT。
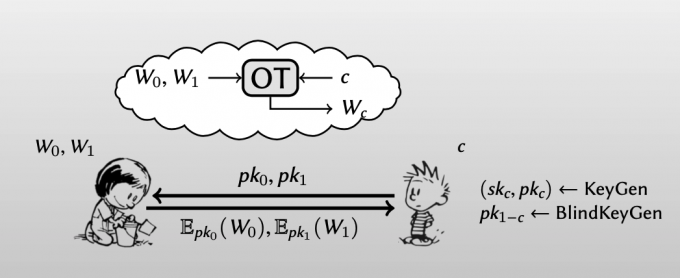
Alice有两个label:W0和W1,Bob想要得到其中一个,假设是Wc ( $c=0,1$ ) 。
Bob需要用KeyGen算法生成一对公私钥 $(sk_c, pk_c)$ ,同样还需要BlindKeyGen算法生成一个不知道(或者硕士无法知道)其对应私钥的公钥 $pk_{1-c}$ 。
- Bob将两个公钥 $pk_0, pk_1$ 发给Alice
- Alice用 $pk_0$ 加密W0,用 $pk_1$ 加密W1,把两个密文发送给Bob
- 因为Bob只知道Wc的私钥,而无法计算得到W1-c的私钥。所以Bob可以从Alice手中得到想要的label。
Need public-key encryption that supports blind key generation:
- sample a public key without knowledge of secret key
- E.g.: ElGamal (sample group element without knowing discrete log)
需要用一些支持blind key生成的公钥加密算法,比如ElGamal,群中的某些元素没有对应的离散对数,也就无法知道其对应的私钥。
Yao’s protocol: overview
Yao协议:
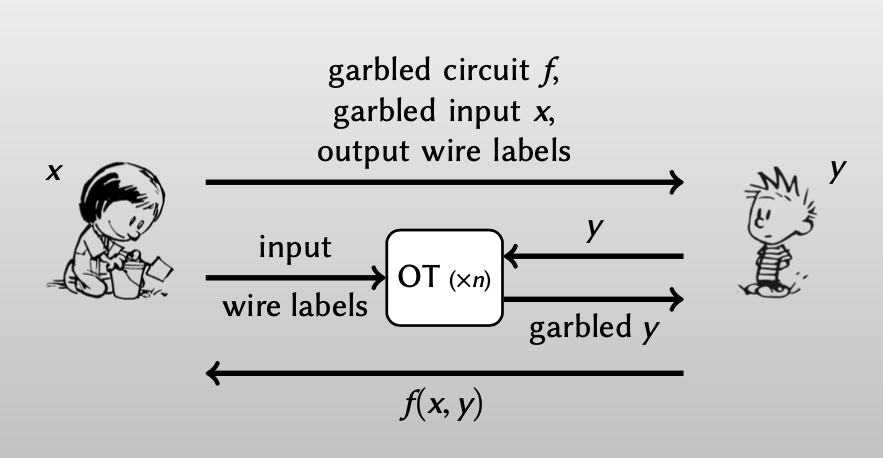
- Gabler生成每个wire的label,把garbled circuit f(加密的真值表)、garbled input x(Alice输入对应的labels)和output wire labels(输出wire对应的labels)发送给Evaluator
- Evaluator用n次OT,在和Alice交互中,得到Bob每一个输入wire的label,每一次OT,Alice都不知道Bob选择的输入是什么。
- 对于Evaluator来说:garbled f + garbled inputs + all output labels ⇒ Bob learns only f(x, y)
「MPC-Mike Rosulek 」:Overview of Secure Computation and Yao's Protocol

