「MPC-Mike Rosulek 」:Oblivious Transfer and Extension
本系列是总结Mike Rosulek教授在上海期智研究院的密码学学术讲座。
这是Mike教授的第三个分享:Oblivious Transfer and Extension
Roadmap
- Precomputation: can compute OTs even before you know your input!
- OT extension: 128 OTs suffice for everything.
OT在多方安全计算中扮演着重要的角色,但OT的实际开销往往很大,因为他不可能使用廉价的加密方法来实现[ImpagliazzoRudich89]。因此在这篇文章中,会介绍一些前沿的方法来提高OT的效率:离线预计算和OT扩展。
Offline Precomputation
Random OT
在提出random OT概念前,我们先回顾一下standard OT:
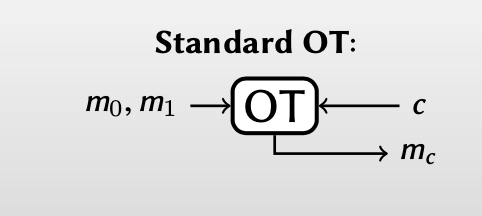
在standard OT中,Alice选择两个输入:$m_0, m_1$,Bob选择一个输入:$c$。
经过一次OT后,Bob可以得到Alice输入中的一个:$m_c$,而不知道另一个输入 $m_{1-c}$ 。而Alice不知道Bob的输入 $c$ ,也就不知道Bob选择的哪一个。
上述过程中,需要双方选择他们各自的输入,双方的输入确定,Bob得到的结果也是确定的:$m_c$ 。
相对于standard OT的确定性,random OT不需要双方选择输入,而是直接随机采样许多 $m_0, m_1, c$ 作为random OT instances。
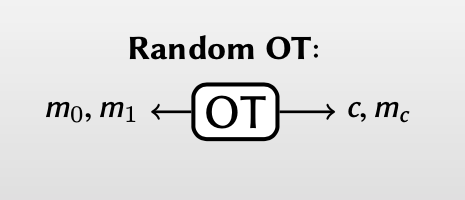
Beaver Derandomization Theorem[Beaver91] :
There is a cheap protocol that securely evaluates an instance of satandard OT using an instance of random OT.
【Beaver的去随机化理论提出:存在一些高效的协议能将一个random OT 转化为一个standard OT instance.】
根据Beaver的去随机化理论,在运行OT协议时,可以先离线生成许多random OTs。在online phase:即OT的输入是由Alice和Bob的输入确定的,可以用Beaver的方法高效地将离线生成的random OT去随机化,即变成standard OT。
Beaver Derandomization
Beaver去随机化过程分为两个阶段:离线阶段和在线阶段(standard OT)
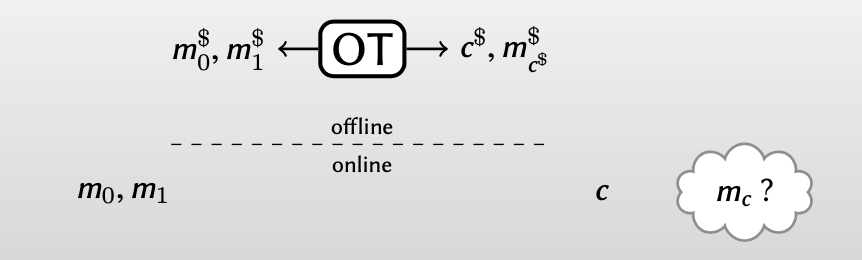
在离线阶段,生成大量random OT instances,其中Alice知道 $m_0^\$, m_1^\$ $ ,Bob知道 $c^\$, m_{c^{\$}}^\$$ 。
而Beaver的去随机化的核心思想是:用生成的random OT instance的 $m_0^\$, m_1^\$ $ 作为one-time pad的密钥,分别加密Alice在线时的输入 $m_0, m_1$ 。而Bob只能用唯一知道的密钥 $ m_{c^{\$}}^\$ $ 解密其中一个,而不知道另一个。
Bob在线时的输入: $c=c^\$$
Bob可以用 $ m_{c^{\$}}^\$ $直接解密: $x_c \oplus m^\$_{c^\$} = x_c \oplus m^\$_c = m_c$ ,得到想要的 $m_c$ ,而对 $m_{1-c}$ 一无所知。
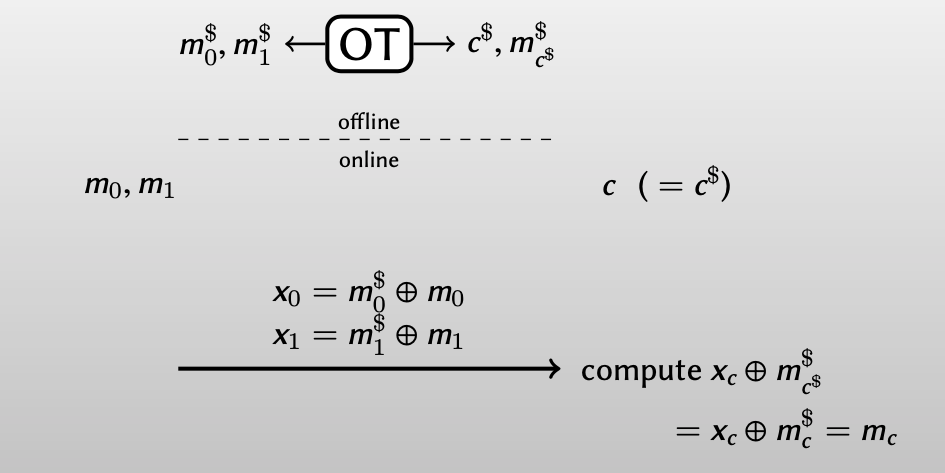
Bob在线时输入: $c\neq c^\$$
如果Bob还想用 $ m_{c^{\$}}^\$ $直接解密得到 $m_c$: $x_c \oplus m^\$_{c^\$} =x_c \oplus m^\$_{1\oplus c} =m_c$ ,Alice在加密时 $m_0, m_1$ 时,必须交换其密钥 $m_0^\$, m_1^\$ $ :
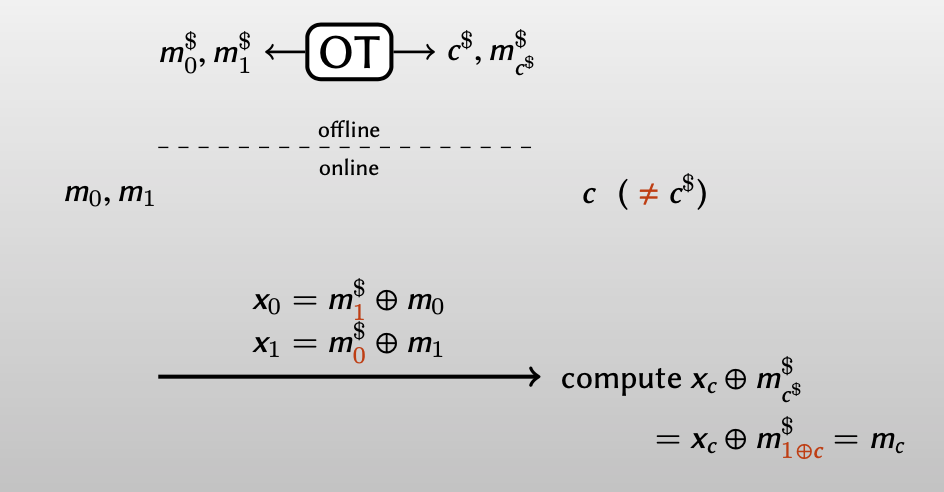
为了Bob能得到正确的 $m_c$ ,Bob应该告诉Alice什么时候要交换密钥,什么时候不用交换密钥。
方法就是用一个1-bit one-time pad,Bob 计算出 $d = c\oplus c^\$$ ,由此告诉Alice是否需要交换密钥($d = 0$ 告诉Alice不需要交换密钥,$d = 1$告诉Alice需要交换密钥),而Alice对 $c, c^\$$ 都一无所知。
因此Beaver的去随机化的完整过程:
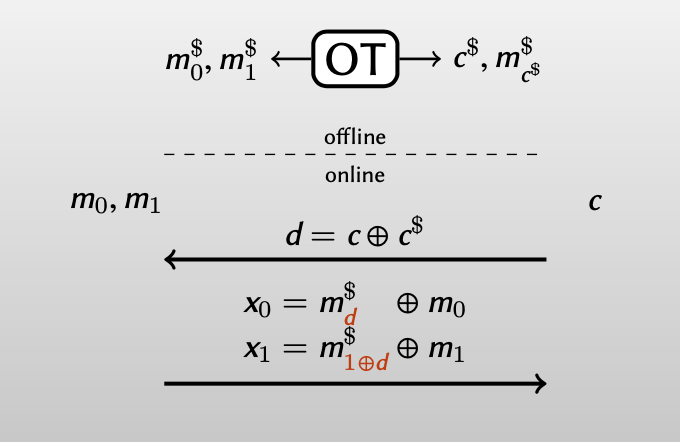
Bob计算出 $d = c\oplus c^\$$ ,发送给Alice,以此告诉Alice是否需要交换密钥 $m_0^\$, m_1^\$ $ 。
Alice输入 $m_0, m_1$ ,根据 $d$ 的值选择密钥 $m_0^\$, m_1^\$ $ 来分别加密$m_0, m_1$ :
$$ \begin{align} x_0 &= m_d^\$ \oplus m_0 \\ x_1 &= m_{1\oplus d}^\$ \oplus m_1 \end{align} $$再将其发送给Bob
Bob用唯一已知的密钥 $ m_{c^{\$}}^\$ $来解密得到 $m_c$: $x_c \oplus m^\$_{c^\$} =x_c \oplus m^\$_{1\oplus c} =m_c$ ,而对 $m_{1-c}$ 一无所知。
最后分析一下Beaver去随机方法的开销:离线阶段生成一个random OT instance和之前的OT开销相同,但在在线阶段,只需要一些简单的异或运算。
OT Extension
An Analogy from Encryption
公钥加密(Public-key encryption, PKE)本质上具有不可避免的高昂开销[ImpagliazzoRudich89] ,但是在现实的加密方案中,可以通过混合公钥加密和对称加密的方式,将实现PKE的开销降到最低。
即PKE of λ bits + cheap SKE = PKE of N bits
Use (expensive) PKE to encrypt short s
【用PKE来加密共享短密钥,比如DH算法】
Use (cheap) symmetric-key encryption with key s to encrypt long M
【再将短密钥通过密钥扩展算法获得长密钥,作为对称加密的密钥】
OT本质上也具有不可避免的高昂开销[ImpagliazzoRudich89] ,所以如果将OT与公钥加密类比,是否存在一种混合加密方案,也能实现λ instances of OT + cheap SKE = N instances of OT?
Beaver OT Extension
Beaver利用Yao的两方安全计算,提出了一种OT的扩展协议[Beaver96] 实现$\lambda$ instances of OT + cheap SKE = $N$ instances of OT.
Beaver OT扩展协议其实是一个两方安全计算电路:该电路将Alice和Bob的输入作为伪随机的种子,以此生成$n$ OT instances,包括输出给Alice的random strings和输出给Bob的choice bits+choice strings。

该电路的输入位是 $\lambda$ bit,因此Alice和Bob需要做 $\lambda$ 次OTs,而该电路可以生成 $n>>\lambda$ OTs,由此实现了$\lambda$ instances of OT + cheap SKE = $N$ instances of OT.
但是用Yao’s garbled circuits的方法实现Beaver OT扩展协议几乎是不可能的,因为这太复杂了。
IKNP Protocol
而Yuval Ishai, Joe Kilian, Kobbi Nissim, Erez Petrank在Crypto 2003年发表的论文:Extending Oblivious Transfers Efficiently,提出了一种可实现、更高效的OT扩展协议,以此实现 $\lambda$ instances of OT + cheap SKE = $N$ instances of OT。
该协议能够用有限的OTs(比如128次OTs)实现足够多次的OTs(比如1 million),下面将详细阐述协议是如何实现的。
IKNP Details
Bob:
has input $r $

$\Rightarrow$ extend to matrix
【把输入 $r$ 重复多次扩展为矩阵 $R$,矩阵的每行 $R_i$ (ith row of $R$)要么是全1或者全0,而且该矩阵的高是million级别的,宽度可以为128】

$\Rightarrow$ secret share as ($T, T’$)
【然后对该矩阵$R$做秘密分享,即拆分为两个矩阵 $T,T’$ 】
【秘密分享的策略是随机生成一个矩阵 $T$ ,而 $T’=T\oplus R$ ,观察下图可以看出 $R_i = T_i \oplus T_i’$ ,即两个矩阵的每行要么相同($r=0$),要么相反($r=1$) 】

Alice:
chooses random string $s$

OT for each column $\Rightarrow$ Alice obtains matrix $Q$
【从列的角度做OT,Alice每次根据 $s$ 的值从Bob的($T,T’$)选择一列,如果 $s_i=0$ ,从矩阵$T$选择第i列,如果 $s_i=1$ ,从矩阵$T’$选择第i列,得到矩阵 $Q$】
【这里的OT中,Bob是sender,Alice是receiver】
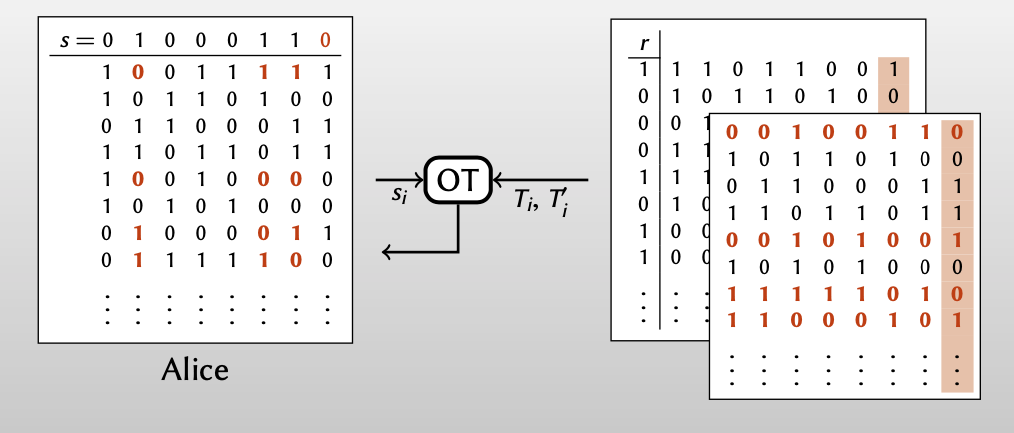
观察Alice经过128次OT得到的矩阵 $Q$ ,可以发现Alice得到的矩阵 $Q$ 和Bob拥有的矩阵 $T$ 有如下关系:
Whenever $r_i = 0$, Alice row = Bob row
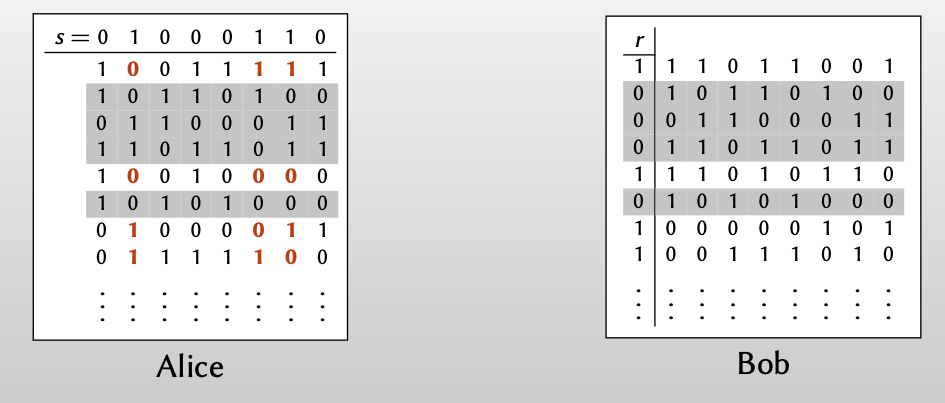
Whenever$r_i =1$, Alice row=Bob row $\oplus s$
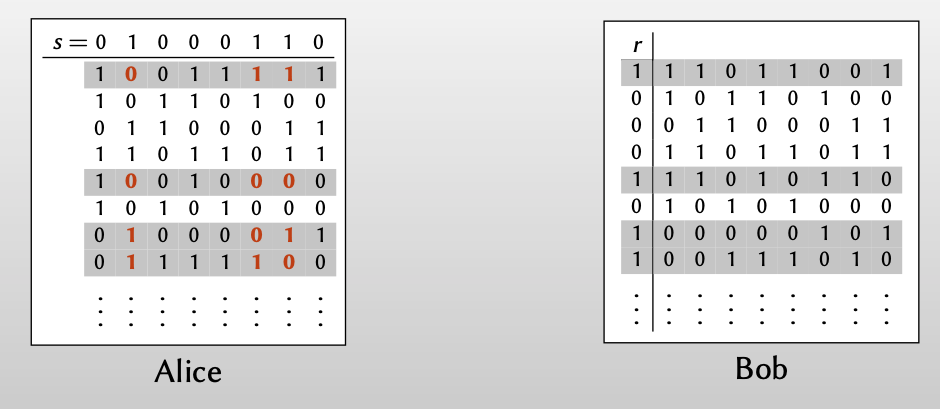
For every i: Bob knows $t_i$ ; Alice knows $q_i$ and $q_i\oplus s$ .
【再从行的角度观察Alice和Bob得到的信息,Alice每次收到 $q_i$ 后,都可以通过和random string $s$ 异或得到 $q_i$ 和 $q_i\oplus s$ ,而这其中的一个值与Bob知道的 $t_i$ 相同】
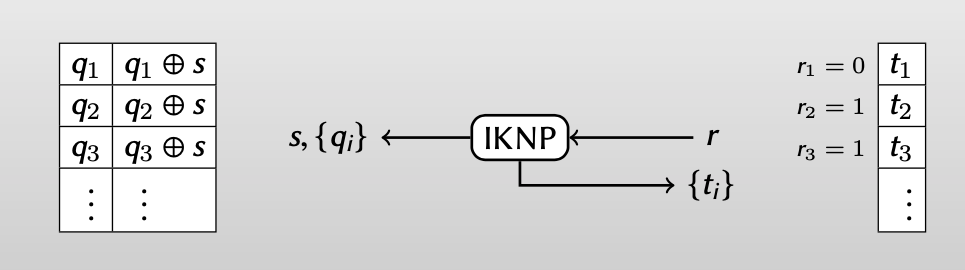
【Alice:因为不知道Bob的 $r_i$ 值,所以不知道Bob选择的 $t_i$ 到底是和 $q_i$ 相等还是和 $q_i\oplus s$ 相等】
【Bob:因为不知道Alice的 $s$ 值,所以只知道选择的 $t_i$ 等于$q_i$ 和$q_i\oplus s$ 中的一个,而不知道另一个】
但是从Bob视角重写Alice得到的信息,我们知道得到:
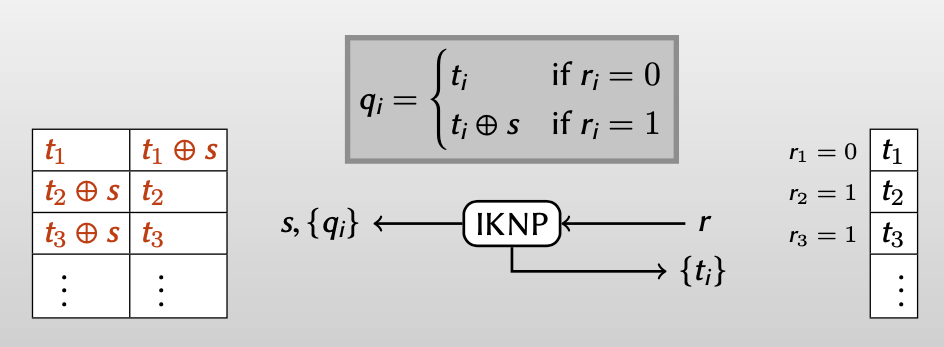
- $r_i=0: q_i=t_i$
- $r_i=1:q_i=t_i\oplus s$
至此,我们几乎已经实现了行角度的OT,Alice有两个值:$q_i$ 和 $q_i\oplus s$ ,Bob根据 $r_i$ 从中选择得到一个,而对另一个一无所知。
Break correlations by applying random oracle
上面我说是“几乎实现了行角度的OT”,为什么是几乎呢?
因为string s的原因,这些OT instances具有一定的线性相关性。所以为了破坏其中的线性相关性,对这些strings都执行一个任意的密码学函数 $H$ :
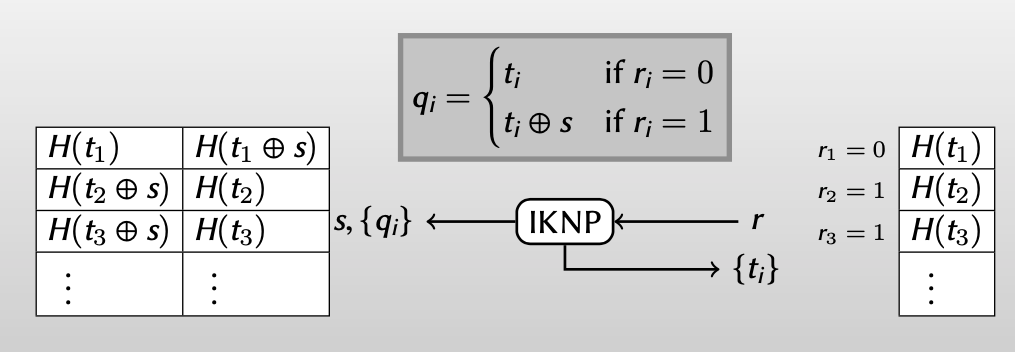
$\Rightarrow$ Random OT instance for each row, using base OT for each column
【由此,通过从列的角度做base OT,得到了足够多的行角度random OT instances】
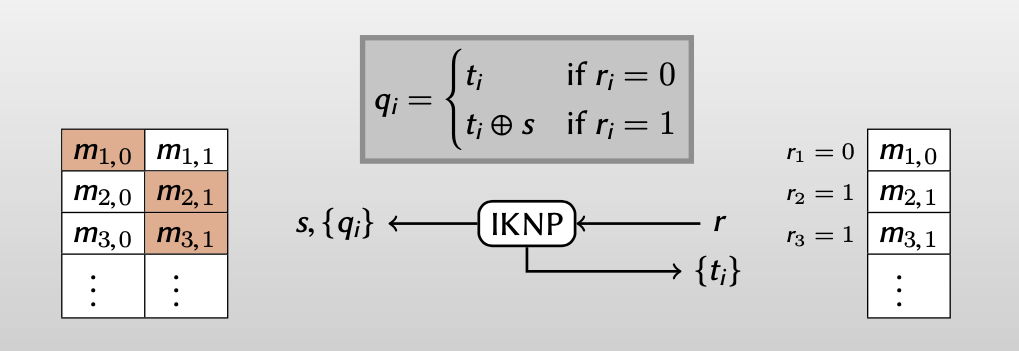
最后,总结一下IKNP如何实现$\lambda$ instances of OT + cheap SKE = $N$ instances of OT。
Bob有一个tall matrix($\lambda$ 列, $n>>\lambda$ 行),Alice从列的角度根据秘密字符串 $s$ 做 $\lambda$ 次base OTs。
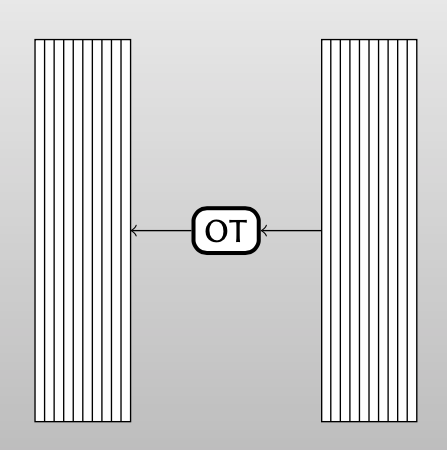
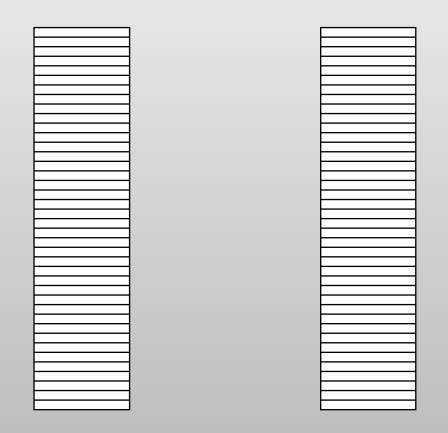
最后Alice和Bob得到了行角度的 $n$ 个扩展OTs。
Malicious Bob in IKNP Protocol
[KellerOrsiniScholl15] 介绍了如果有恶意的参与方,IKNP受到的威胁
假设Bob是恶意的:
Bob:
有一个输入 $r $
$\Rightarrow$ 对其扩展为矩阵 $R$ ,但是恶意地翻转了 $t_2$ 的第二位bit:
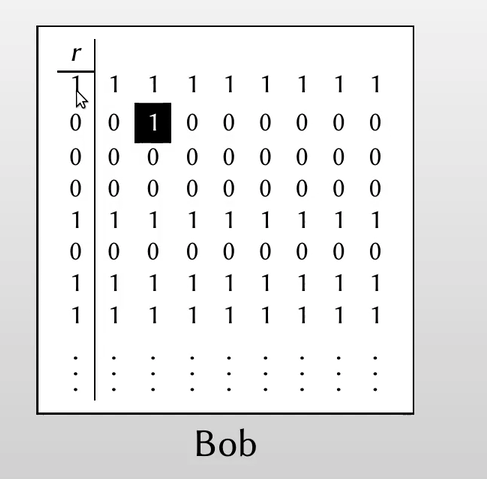
$\Rightarrow$再做秘密共享为 ($T, T’$) ,同样的,$T’$ 中也有一位被翻转了:
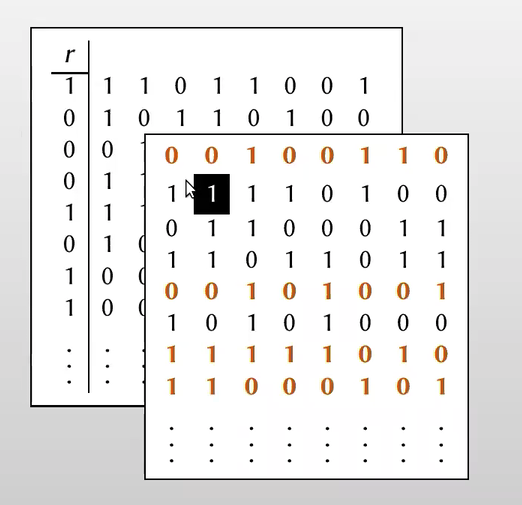
Alice:
选择一个随机串 $s$
对每列做OT $\Rightarrow$ Alice得到矩阵 $Q$
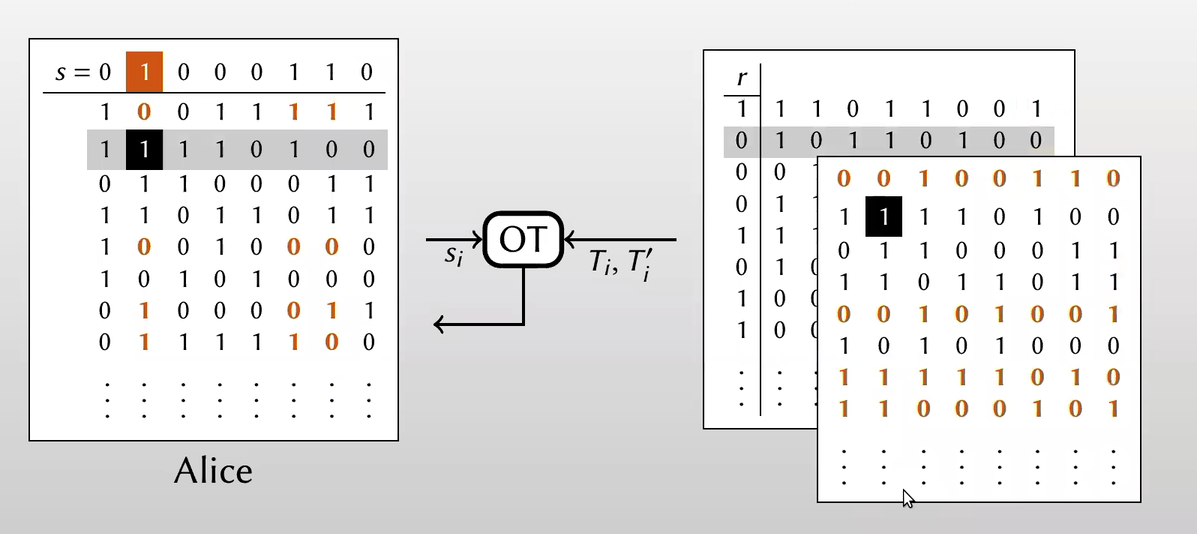
因为 $r_2=0$ ,本应该有 $q_i = t_i$ 。但因为Bob恶意翻转了一位,所以Alice得到的 $q_i$ 和 $t_i$ 在第二位不同
…
所以在Alice和Bob同时使用 $H(row)$ 破坏线性相关性后,Bob会发现得到的 $H(row#2)$ 值不同,Bob就知道Alice选择的随机串中 $s_2=1$ 。
如此以来,Bob每次都恶意翻转某一列的一个bit,就可以学到 $s$ 的所有比特信息。
Consistency Check
所以如何保证Bob没有恶意篡改矩阵 $R_i$ ($R$ 矩阵的第i行)?
[KellerOrsiniScholl15] 提出了一种一致性检验方法来检测Bob是否恶意篡改了矩阵。

Alice在执行IKNP中通过多次检验上述方程的一致性,来检测Bob是否恶意篡改了扩展矩阵。
同时,为了保护扩展矩阵的位信息,Bob也使用一个随机矩阵来加密 $R^*$ 。
IKNP可以通过上述一致性检验来实现malicious security,而引入的额外开销很小。
Generalizing IKNP
IKNP协议生成了许多二选一的OT instances,这里将介绍如何对IKNP协议一般化,以生成多选一的OT instances。
再次回顾一下IKNP的做法:
Bob有一个选择串 $r$

扩展为矩阵 $R$ ,矩阵的每行是全0或全1

再对矩阵R做秘密分享
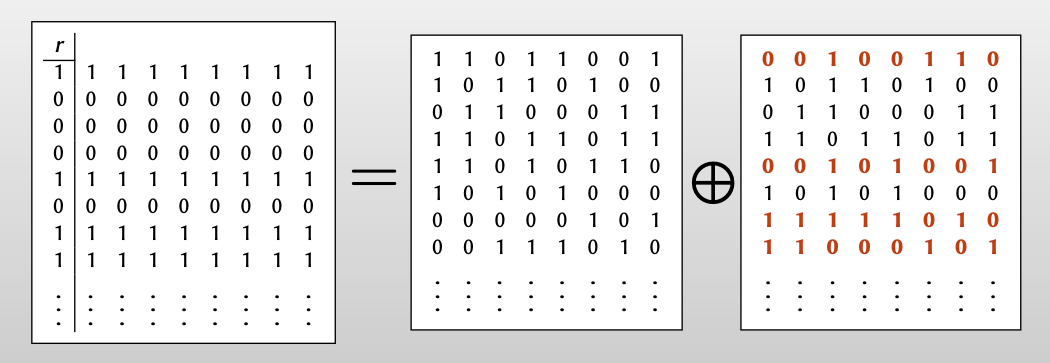
从行的角度看矩阵扩展,把0 编码为 000... ,把1 编码为111... 。所以可以把矩阵扩展看作对 $r$ 的bit的一种编码方式(repetition code)。
因此,一般化IKNP的核心思想就是:用具有差错校正的编码方式对 $r$ 的bit进行编码。
Coding view of IKNP
现在,我们从编码的方式看IKNP。
Bob:
Bob 有一个输入 $r$
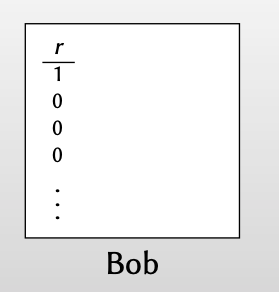
对 $r$ 的比特进行编码:

在这种编码方式下进行秘密分享
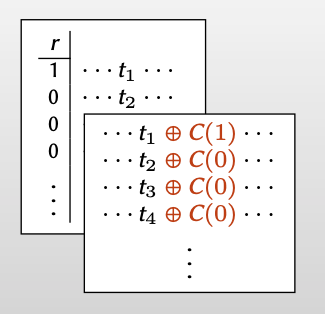
Alice 对每列做OT,得到矩阵$Q$
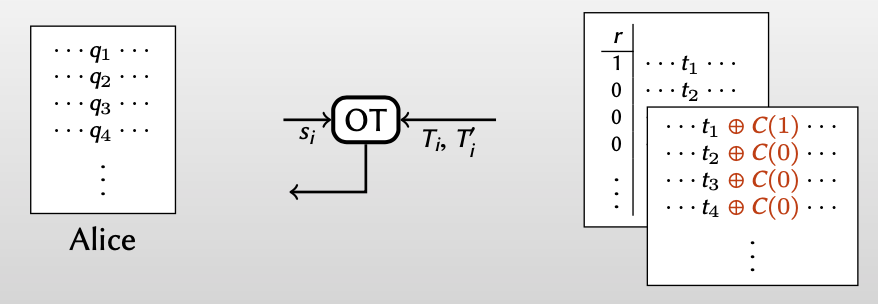
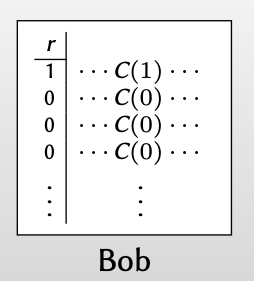
Bob得到的 $t_i$ 和Alice得到的 $q_i$ 有如下关系:$t_i = q_i\oplus C(r_i)\wedge s$
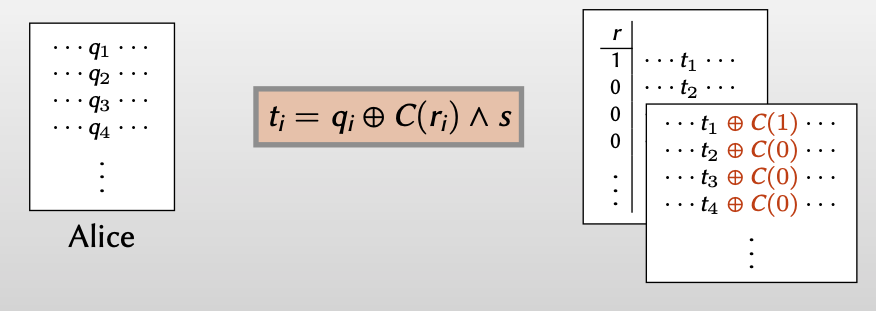
如果是在编码$C(0)=000…, C(1)=111…$ 下:
- $r_i=0 \Rightarrow t_i = q_i\oplus (000…)\wedge s=q_i$
- $r_i=1 \Rightarrow t_i=q_i\oplus (111…)\wedge s=q_i\oplus s$
For every i: Bob knows $t_i$; Alice knows $q_i\oplus C(0)\wedge s$ and $q_i\oplus C(1)\wedge s$
【此时Alice知道$q_i\oplus C(0)\wedge s$ 和 $q_i\oplus C(1)\wedge s$ ,Bob知道$t_i$ 】
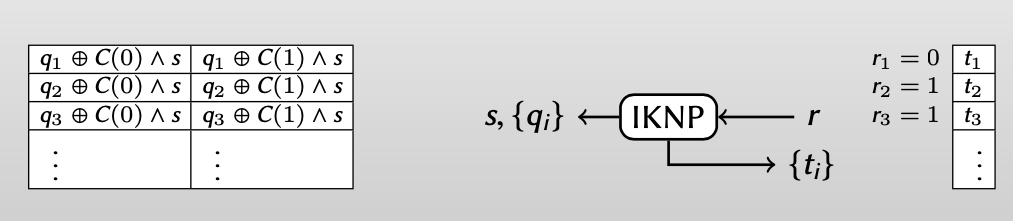
从Bob的视角重写Alice得到的 $q_i=t_i\oplus C(r_i)\wedge s$

当$C$是一种线性编码时,即满足: $[C(a)\wedge s]\oplus [C(b)\wedge s]=C(a\oplus b)\wedge s$ and $C(0)\wedge s = 000…$
得到:
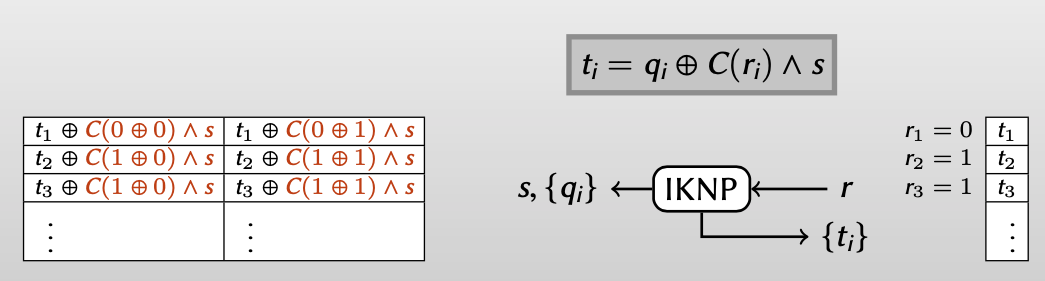
化简:
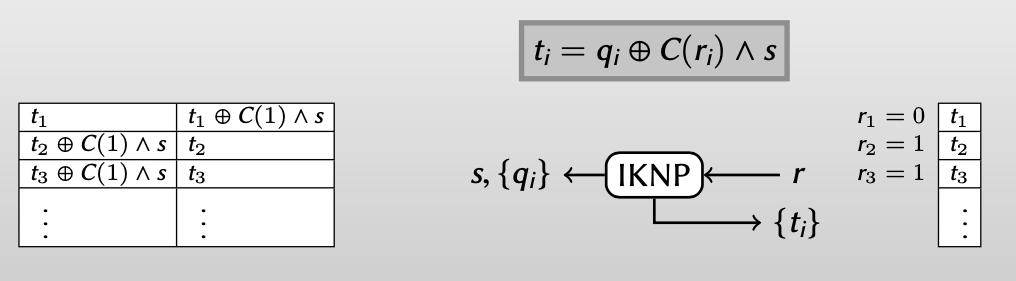
Use random oracle to destroy correlations
【再破坏其线性相关性】
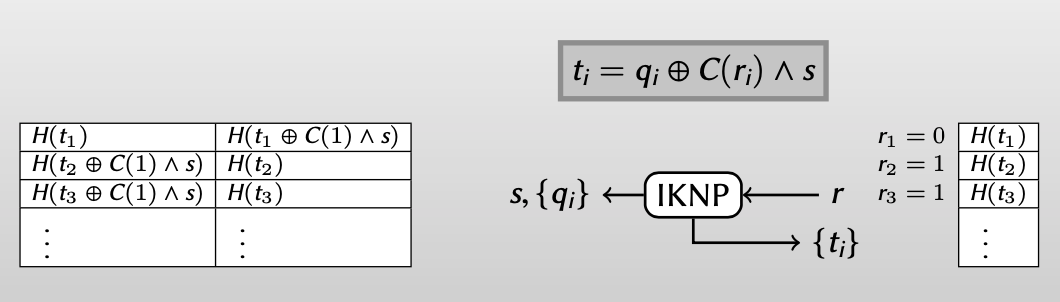
Generalizing IKNP
刚刚我们考虑的是只对 $\{0, 1\}$ 编码,即: $C:\{0, 1\}\rightarrow \{0, 1\}^k$ 编码。
现在考虑编码更多的bits,即 $C:\{0, 1\}^3\rightarrow \{0, 1\}^k$ ,同样地,$C$是线性编码。
同样的运行IKNP:
For every i: Alice can compute 8 (things)
【之前Alice是可以计算$q_i\oplus C(0)\wedge s$ 和 $q_i\oplus C(1)\wedge s$ 】
现在是对 $\{0, 1\}^3$ 编码,就可以计算:
$q_i\oplus C(000)\wedge s, q_i\oplus C(001)\wedge s, \cdots,q_i\oplus C(111)\wedge s$

同样的,从Bob的角度重写Alice得到的值$q_i=t_i\oplus C(r_i)\wedge s$
并且 $C$ 是线性编码,满足$[C(a)\wedge s]\oplus [C(b)\wedge s]=C(a\oplus b)\wedge s$ and $C(0)\wedge s = 000…$ ,化简后:
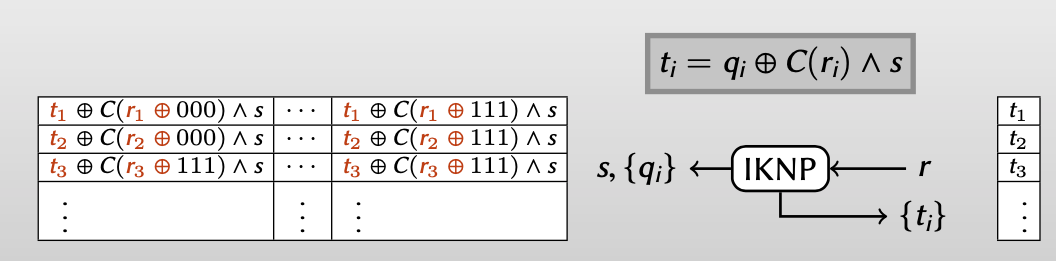
对上述Alice计算出的8个串,Bob只知道其中的一个 $t_i$ ,而这个 $t_i$ 等于Alice知道的第几个串,这取决于Bob的选择的 $r_i$ ,使得 $C(r_i\oplus \cdots)=000…$ 。
In the random oracle model: $H(t_1 \oplus c_1 \wedge s),…H(t_n \oplus c_n \wedge s)$ pseudorandom if all $c_i$ have Hamming weight $\ge \lambda$
【在破坏线性相关性时,只有当所有 $c_i$ 的汉明重量(Hamming weight)$\ge\lambda$ 时,$H(\cdot)$ 和随机串才具有不可区分性】
汉明重量(Hamming weight):汉明重量是一串符号中非0符号的个数。
汉明距离(Hamming distance):两个字符串对应位置的不同字符的个数。
就此,我们介绍了扩展的IKNP协议,[KolesnikovKumaresan13] 提到使用这样的编码: $C:\{0, 1\}^l\rightarrow \{0, 1\}^k$ (编码字符串的汉明距离 $\ge \lambda$) 执行 $k$ 次base OT,就能实现从 $2^l$ 中选一个的OT扩展(1-out-of- $2^l$ OT extension)。
1-out-of-256 OT[KolesnikovKumaresan13] :
Walsh-Hadamard code $C:\{0, 1\}^8\rightarrow \{0, 1\}^k$ (min. dist. 128)
1-out-of- $2^{76}$ OT[OrruOrsiniScholl16] :
BCH code $C:\{0, 1\}^{76}\rightarrow \{0, 1\}^{512}$ (min. dist. 171)
1-out-of-∞ OT[KolesnikovKumaresanRosulekTrieu16]
这篇文章提出,对于任意的伪随机编码$C:\{0, 1\}^*\rightarrow \{0, 1\}^{~480}$ ,只需要满足最小的hamming dist.,而不用要求编码 $C$ 的线性性质,就可以实现1-out-of-∞ OT。
就此,IKNP协议的介绍到此结束。也正是因为IKNP协议,使得OT的效率大幅提高。
「MPC-Mike Rosulek 」:Oblivious Transfer and Extension

