「Cryptography-Boneh」:Block Cipher 1
这篇文章介绍了块密码。
文中主要分为四个部分。
第一个部分解释了块密码的基础概念,包括抽象概念PRF(伪随机函数)和PRP(伪随机置换)的定义及其安全定义。
第二个部分介绍了经典块密码DES,包括DES的Feistel网络,支撑Feistel网络的Luby-Rackoff定理,triple-DES和对DES的一些攻击方法。特别是有效的中间相遇攻击。
第三个部分介绍了目前流行的块密码AES,包括AES的结构和一些攻击方法等。
最后一小部分介绍了用PRG构造PRF,再利用Feistel网络变成块密码。
Overview
块密码,简单来说,就是在给定密钥 (k bits)下,将输入块(n bits)映射到输出块(n bits)。
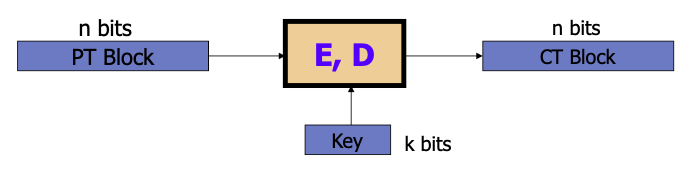
比如,在3DES中,n = 64 bits, k = 168 bits;在AES中,n = 128 bits, k = 128, 192, 256 bits。
块密码算法一般是通过迭代(iteration)实现的,如下图的结构:
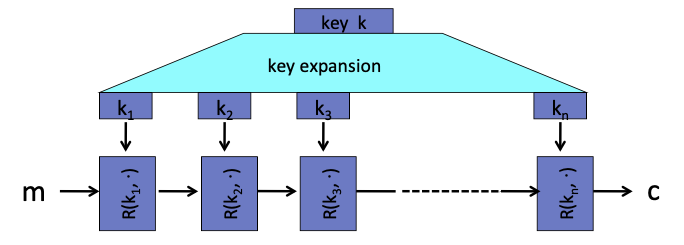
密钥k通过密钥扩展(key expansion)得到一系列轮密钥。
明文块m通过迭代运算,得到最终的密文c,其中每一次运算称为轮函数R(k, m)。
对于3DES来说,轮数为n = 48,对于AES-128来说,轮数为n = 10。
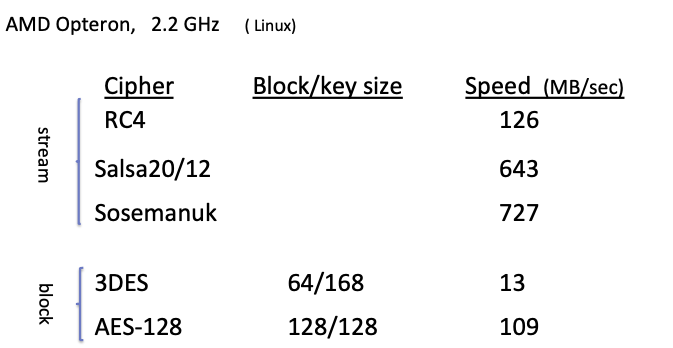
虽然迭代运算会让块密码比流密码慢很多,但块密码有很多应用。
PRPs and PRFs
这里介绍两个抽象的概念,伪随机置换(PRP)和伪随机函数(PRF)。
Pseudo Random Function(PRF):
defined over(K, X, Y): $F:K\times X \rightarrow Y$ such that exists “efficient” algorithm to evaluate F(k, x)
【伪随机函数定义在(K, X, Y)上,只要求是可计算的,没有要求是可逆的】
Pseudo Random Permutations(PRP):
defined over(K, X): $E:K\times X\rightarrow X$ such that:
- Exists “efficient” deterministic algorithm to evaluate E(k, x)
- The function E(k, ·) is one to one
- Exists “efficient” inversion algorithm D(k, y)
【而伪随机置换定义在(K, X)上,除了要求是可计算的,还要求是一对一映射(单射),即存在可逆运算】
块密码都是PRPs(不然怎么解密),常见的PRP有3DES,AES等:
AES: $K \times X \rightarrow X$ where K = X = $\{0, 1\}^{128}$
3DES: $K\times X \rightarrow X$ where X = $\{0, 1\}^{64}$ , K = $\{0, 1\}^{168}$
从定义上来说,任何PRP都是PRF;但一个PRF是PRP的充分条件是X=Y,且存在可逆运算(efficiently invertible)。
Secure PRFs
在介绍PRF的安全性之前,先定义一些符号:
$F: K \times X \rightarrow Y$ is a PRF.
Funs[X, Y]: the set of all functions from X to Y
【X到Y的所有映射关系】
$S_F={ F(k, \cdot)}$ s.t. $k\in K$ $\subseteq$ Funs[X, Y]
【确定k就确定了一种X到Y的映射关系】
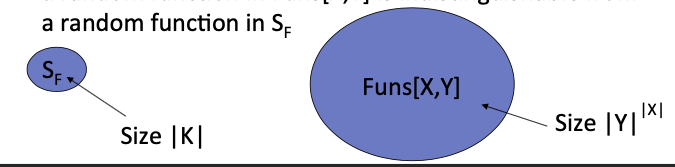
直觉上来说,当从Funs[X, Y]中随机采样的函数与从 $S_F$ 中随机采样的函数不可区分时,PRF是安全的。
Intuition: a PRF is secure if a random function in Funs[X, Y] is indistinguishable from a random function in $S_F$ .
定义下图的游戏:
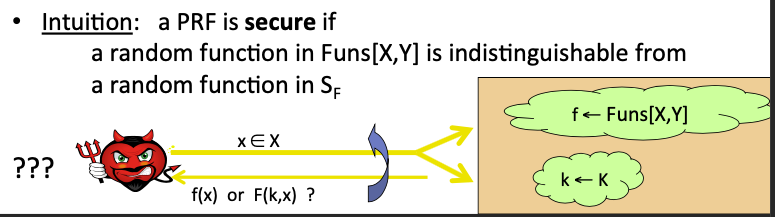
云从Funs[X, Y]中随机选取一个函数f,并随机选择一个k,即确定了一个在 $S_F$ 中函数。
攻击者向云多次询问x的计算结果,对云来说,如果是b = 0,他返回f(x),如果b = 1,他返回F(k, x)。
当攻击者输入任意输入x时,都无法区分计算结果是f(x)计算的还是F(k, x)计算的,PRF是安全的。
Secure PRPs/Block Ciphers
块密码都是PRP,所以这里也在定义什么是安全的块密码。
同样定义一些符号:
$E: K\times X\rightarrow Y$ is a PRP ( X = Y).
Perms[X, Y]: the set of all one-to-one functions from X to Y
【X到Y的所有的一对一映射关系】
$S_F={ E(k, \cdot)}$ s.t. $k\in K$ $\subseteq$ Perms[X, Y]
【确定k就确定了一种X到Y的一对一映射关系】
同样,当从Perms[X, Y]中随机采样的函数与从 $S_F$ 中随机采样的函数不可区分时,PRP是安全的。
Intuition: a PRP is secure if a random function in Perms[X, Y] is indistinguishable from a random function in $S_F$ .
定义下图的游戏:
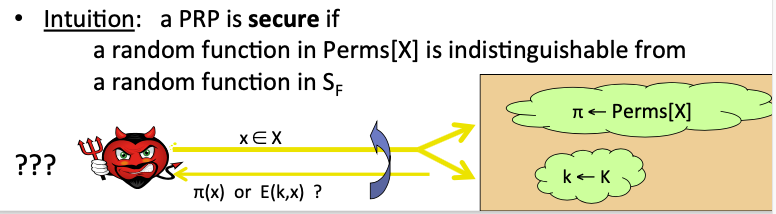
云从Perms[X, Y]中随机选取一个函数 $\pi$ ,并随机选择一个k,即确定了一个在 $S_F$ 中函数。
攻击者向云多次询问x的计算结果,对云来说,如果是b = 0,他返回$\pi(x)$,如果b = 1,他返回F(k, x)。
当攻击者输入任意输入x时,都无法区分计算结果是$\pi(x)$计算的还是F(k, x)计算的,PRP是安全的。
注意:这里是对任意输入,如果对某一个输入,攻击者能区分,这个PRP都是不安全的。
PRF $\rightarrow$ PRG
PRF的一个简单应用是把它变成一个PRG。
Let $F: K\times \{0, 1\}^n\rightarrow \{0, 1\}^n$ be a secure PRF.
The following $G: K\rightarrow \{0,1\}^{nt}$ is a secure PRF:
$$ G(k) = F(k, 0)\mid\mid F(k, 1) \mid\mid \dots \mid\mid F(k, t-1) $$这是一种计数器模式,计数器模式最显著的优点是可并行计算。
此外该PRG的安全性来自于PRF的安全性,即F(k, ·)与f(·)不可区分。
DES
Data Encryption Standard(DES)
DES的核心就是Feistel网络结构:
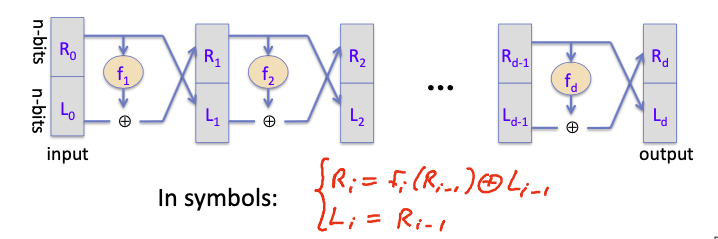
- $R_i = f_i(R_{i-1})\oplus L_{i-1}$
- $L_i = R_{i-1}$
对于给定的函数的轮函数 f1, …, fd: $ \{0,1\}^n\rightarrow \{0,1\}$ ,Feistel网络结构都可以构造出2n bits的可逆函数: $ F: \{0,1\}^{2n}\rightarrow \{0,1\}^{2n}$
Claim: for all f1, …, fd: $ \{0,1\}^n\rightarrow \{0,1\}$ , Feistel network $ F: \{0,1\}^{2n}\rightarrow \{0,1\}^{2n}$ is invertible.
证明:构造出可逆函数即可
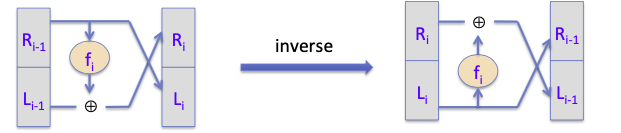
- $R_{i-1} = L_i$
- $L_{i-1}=R_i\oplus f_i(L_i)$
需要注意的是,在解密电路中,轮函数的使用如下图是逆序使用的。
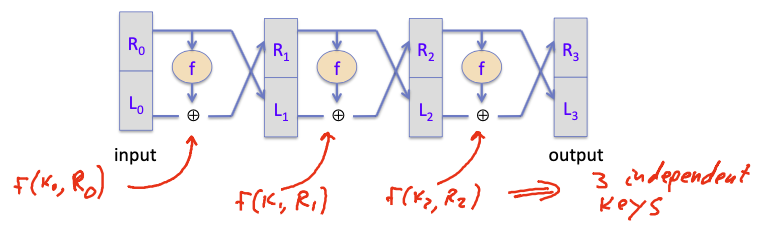
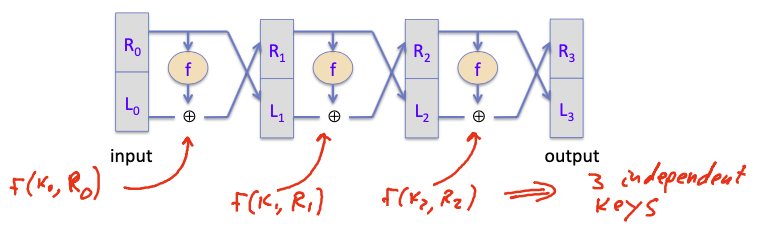
Luby-Rackoff’85 Thm
支撑Feistel Network安全性的一个理论是Luby-Rackoff的一个定理,这将安全的PRF变成安全的PRP,这也是块密码(使用Feistel结构的块密码)安全性的支撑。
Thm:
$f:K\times \{0,1\}^n\rightarrow \{0,1\}^n$ a secure PRFthen, 3-round Feistel $F: K^3\times{0,1}^{2n}\rightarrow {0,1}^{2n}$ a secure PRP.
DES Structure
DES的核心是一个16轮的Feistel的网络。
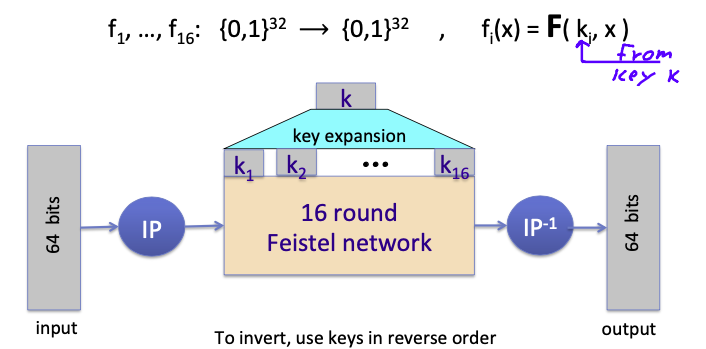
DES的输入是64 bits块,通过一个初始置换(IP),该置换并不是为安全性服务的,只是DES标准里的要求。
然后再通过16轮的Feistel网络,在Feistel网络中依次调用轮函数,轮函数中的轮密钥是通过初试密钥扩展得到的16个不同密钥。
最后再通过逆置换得到64 bits的输出块。
The function F(ki, x)
DES的轮函数结构如下图:
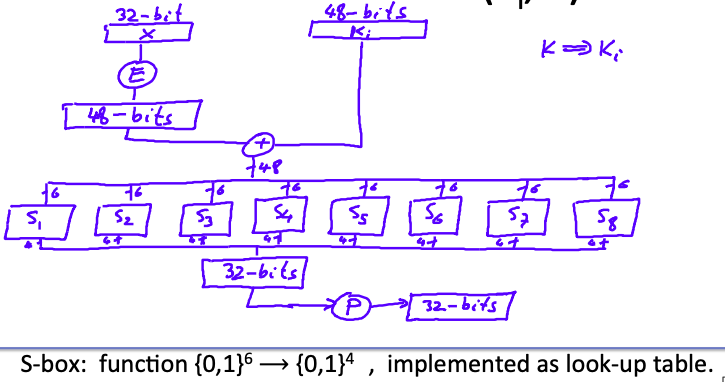
轮函数的输入是32 bits x和48 bits的密钥ki:
32 bits x通过expansion box,扩展为48 bits。扩展方式只是复制一些位。
扩展后的x与轮密钥ki进行异或运算。
异或运算后的结果为48 bits,再被划分为8组6 bits,每一组都通过一个S-box,每一个S-box实则是一个非线形映射 ${0,1}^6\rightarrow {0,1}^4$ ,在实现中往往使用查表的形式使用。

通过S-box后,又得到了32 bits,最后通过一个置换(Permutation),得到该轮的最终输出。
S-box
S-box也是DES中最重要的一部分,因为他是DES中唯一的非线性部分,它保证了整个DES的非线形映射关系。
来看一个糟糕的S-box的例子: $\mathrm{S}_{\mathrm{i}}\left(\mathrm{x}_{1}, \mathrm{x}_{2}, \ldots, \mathrm{x}_{6}\right)=\left(\mathrm{x}_{2} \oplus \mathrm{x}_{3}, \mathrm{x}_{1} \oplus \mathrm{x}_{4} \oplus \mathrm{x}_{5}, \quad \mathrm{x}_{1} \oplus \mathrm{x}_{6}, \quad \mathrm{x}_{2} \oplus \mathrm{x}_{3} \oplus \mathrm{x}_{6}\right)$
上式也可以写做: $\mathrm{S}{\mathrm{i}}(\mathbf{x})=\mathrm{A}{\mathrm{i}} \cdot x(\bmod 2)$
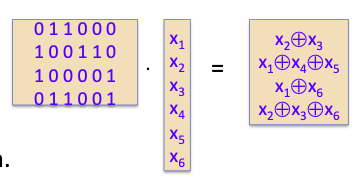
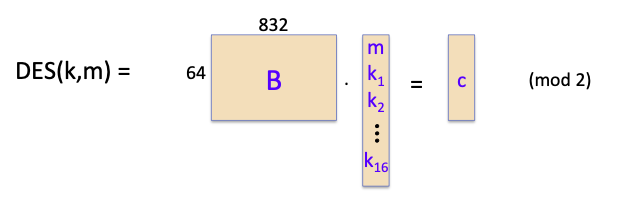
我们称上面的S盒是一个线性函数。
这会带来什么影响呢?如果S盒是线性的,那么整个DES都会变成线性的,即存在一个确定的二元矩阵 $\mathbf{B}$ 满足:

而该线性关系还有一个简单的检验方法:

Exhaustive Search Attacks
DES的密钥空间比较小,因此可以使用穷举密钥的方法攻击。
对于已知的一些明文-密文对,我们希望穷举攻击能得到唯一的一个密钥,而不是说对于一个明文-密文对,有多个密钥(映射关系)都符合。
因此支撑穷举攻击DES的一个定理是:
假设DES是一个理想的密码,即 $2^{56}$ 个密钥对应 $2^{56}$ 个不同的随机可逆函数,那么对于任意的明文-密文对($c = \mathrm{DES}(k,m)$) ,最多只有一个密钥的概率大于 99.5%。
证明:
假设存在一个密钥k’,不是真正的密钥k,但满足 $c = \mathrm{DES}(k’, m)=\mathrm{DES}(k,m)$ 。
这样的概率是小于 所有 $2^{56}$ 个密钥都满足该明文-密文对的概率。

因此,如果已知两个明文-密文对,那么通过这两个DES pairs就可以以 $1-1/2^{71}$ 的概率确定出正确的密钥。
同样,对于AES-128来说,通过两个AES pairs就可以以 $1-1/2^{128}$ 的概率确定出正确的密钥。
Strength DES against ex. search
因为DES的密钥空间实在是太小了,所以有一个DES challenge的挑战,随着计算能力的发展,破解DES的速度越来越快。

1: Triple-DES
一个抵御DES穷举攻击的算法是Triple- DES。
- Let $\mathrm{E}:\mathrm{K}\times \mathrm{M}\rightarrow \mathrm{M}$ be a block cipher.
- Define $\mathrm{3E}: \mathrm{K}^3\times \mathrm{M}\rightarrow \mathrm{M}$ as $\mathrm{3E}((\mathrm{k_1},\mathrm{k_2},\mathrm{k_3}),\mathrm{m})=\mathrm{E}(\mathrm{k_1},\mathrm{D}(\mathrm{k_2},\mathrm{E}(\mathrm{k_3},\mathrm{m})))$
triple- DES为什么是E、D、E的运算顺序,而不是E、E、E的运算顺序?
因为对于Triple- DES来说,如果 $k_1=k_2=k_3$ ,就变成了single DES(虽然在运算速度上,没有什么必要)
Triple- DES的密钥空间大小是 $3\times 56=168$ bits,在运算上会比DES慢三倍,但攻击triple- DES只需要 $O(2^{118})$ 的时间复杂度。(下文介绍的中间相遇攻击)
Meet in the middle attack
为什么不用double DES?
因为有一种中间相遇攻击(meet in the middle attack),让攻击double DES的时间和穷举攻击single DES的时间差不多。
如果我们使用double DES,$\mathrm{2E}((\mathrm{k_1},\mathrm{k_2}),\mathrm{m})=\mathrm{E}(\mathrm{k_1},\mathrm{E}(\mathrm{k_2},\mathrm{m}))$

double DES的密钥空间为112 bits,但在中间相遇攻击下,穷举范围可以少一半比特。
中间相遇攻击的核心思想是,我们希望找到 $(k_1, k_2)$ 满足 $E(k_1, E(k_2, M))=C$ ,即满足:$E(k_2,M)=D(k_1, C)$ 。
Attack: M = (m1, …, m10), C = (c1, …, c10)
build table and sort on 2nd column.
从double DES 的左边的明文开始,枚举 $k_2$ ,计算 $E(k^i, M)$ 的值,最后按照 $E(k^i, M)$ 的值排序。

for all $k\in {0,1}^{56} do:$ test if $D(k,C)$ is in 2nd column.
从double DES的右边的密文开始检测,是否 $D(k,C)$ 存在在上述表中,如果 $E(k^i, M)=D(k,C)$ ,那么就得到了 $(k^i, k)=(k_2, k_1)$
分析一下攻击时间,第一部分是建表排序,第二部分是计算二分查表的时间。
Time = $2^{56} \log \left(2^{56}\right)+2^{56} \log \left(2^{56}\right)<2^{63}<<2^{112}, \quad \text { space } \approx 2^{56}$
同样的,中间相遇攻击同样可以应用于3DES中:$\text{Time}=2^{118},\quad \text{space}\approx 2^{56}$
2: DESX
$\mathrm{E}: \mathrm{K} \times{0,1}^{n} \rightarrow{0,1}^{\mathrm{n}} \text { a block cipher }$
Define EX as $\operatorname{EX}\left(\left(\mathrm{k}{1}, \mathrm{k}{2}, \mathrm{k}{3}\right), \mathrm{m}\right)=\mathrm{k}{1} \oplus \mathrm{E}\left(\mathrm{k}{2}, \mathrm{~m} \oplus \mathrm{k}{3}\right)$
对于DESX来说,密钥空间长度为: 64+56+64 = 184 bits,但同样的通过中间相遇攻击,time = $2^{64+56}=2^{120}$ .
需要注意的一点是,在实际使用中,有人使用 $\mathrm{k}{1} \oplus \mathrm{E}\left(\mathrm{k}{2}, \mathrm{m}\right) \text { and } \mathrm{E}\left(\mathrm{k}_{2}, \mathrm{m} \oplus \mathrm{k}_{1}\right)$ 的设计,这样的设计和原始DES一样易收ex. search的攻击。(通过中间相遇攻击)
More attacks on block ciphers
Attacks on the implementation
对于DES,还有一些针对实现上的攻击。
第一种是侧信道攻击(Side channel attacks),通过测量加密解密时的时间差异、能源消耗差异来得到一些额外的信息。

另一种是Fault attacks,通过最后一轮的计算错误可能会暴露密钥k。
对于实现上的攻击的经验教训是:除了不要自己设计密码学算法,甚至都不要自己去实现。
Linear and differential attacks
该攻击的目标是,给定许多inp/out pairs,希望能在比 $2^{56}$ 更少的时间内攻击成功。
Linear cryptanalysis (overview):
let c = DES(k, m), suppose for random k, m:

第一部分是msg bits的子集合,第二部分是密文bits 的子集合,第三部分是key bits的子集合。
如果这些都是相互独立的,那么这个概率应该为1/2,但因为有slightly 线性的关系,所以这个概率会有一点bias。对于DES来说,因为第五个S-box的一点bug,$\varepsilon=1/2^{21}\approx 0.0000000477$ .
Thm:

基于上述线性的关系,该定理表示如果给了 $1/ \varepsilon^2$ 个随机明文密文对,大部分都满足上式比特集合的线性关系。
所以,对于DES来说,$\varepsilon=1/2^{21}$ ,通过 $2^{42}$ 个inp/out pairs能在 $O(2^{42})$ 时间内得到 $k[l_1,…,k_u]$ 比特集异或的结果。
但其实不止是xor of key bits,实际上: can find 14个key bits in time $2^{42}$ 。(todo)
这样就将穷举攻击的复杂度降低到56-14=42 bits in time $2^{42}$
Total attack time $\approx 2^{43}<<2^{56}$ with $2^{42}$ random inp/out pairs.
Lesson:
A tiny bit of linearly in $S_5$ lead to a $2^{42}$ time attack.
So don’t design ciphers yourself.
Quantum attacks
另一个针对穷举攻击的解决方法是量子攻击。
对于一个一般的搜索问题:

一般计算机解决该类问题的最优时间是 $O(|X|)$ ,而量子计算机解决该类问题的最优时间是 $O(|X|^{1/2})$ 。
不过,量子计算机是否被实现还是一个疑问。
用量子计算机来穷举密钥空间,只需要 $O(|K|^{1/2})$ 的时间即可找到密钥。
AES
AES的发展过程如图:

AES不是Feistel网络结构的密码,他是一个替换-置换类网络(Subs-Perm network):
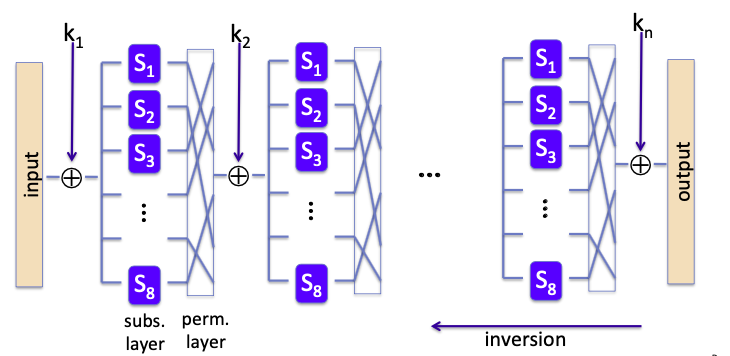
AES-128 schematic
AES-128的结构如下图:
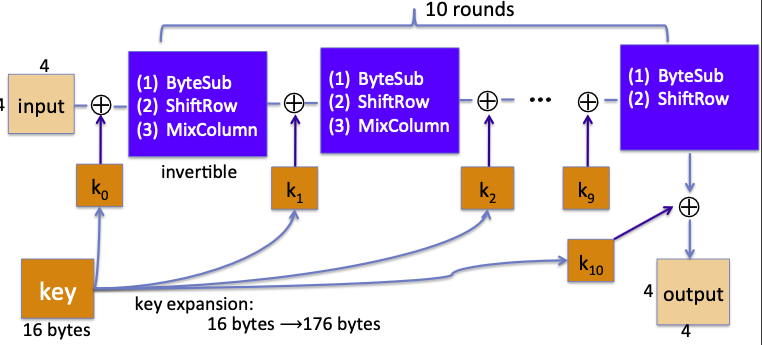
输入块是16 bytes的4*4矩阵,通过10轮运算得到最后的输出块。
每一轮都包括同样的操作(除了最后一轮不太一样),密钥加,字节替换(ByteSub),行移位(ShiftRow),列混淆(MixColumn)。其中每一轮的轮密钥是初始16 bytes的密钥通过密钥扩展得到的。
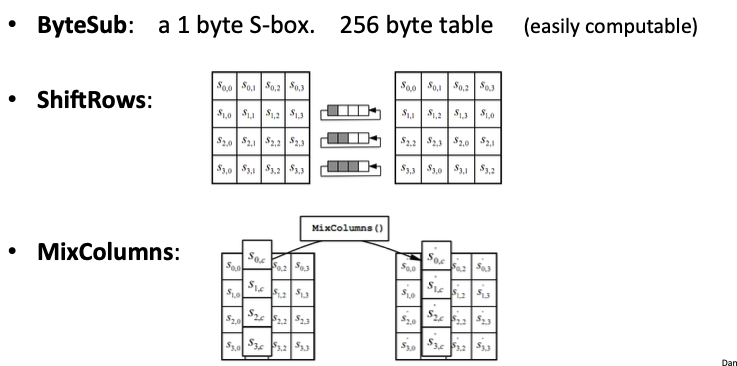
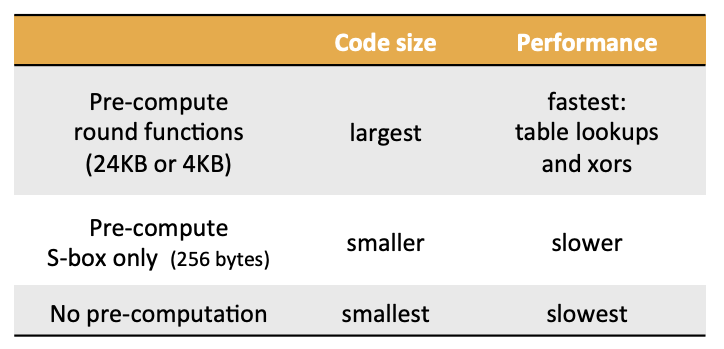
轮密钥中的字节替换可以通过预计算查表的形式,也可以通过直接运算的形式。因此在实际应用中可以根据需求做出权衡。
AES in hardware
为了加快AES的运算速度,各公司有设计相关指令。
AES instructions in Intel Westmere:
aesenc, aesenclast: 执行AES中的一轮运算
- 128-bit registers: xmm1=state, xmm2=round key
aesenc xmm1, xmm2:执行一轮运算,并把计算结果放在xmm1中
aeskeygenassist: 执行AES的密钥扩展。
同样的硬件上,相对于OpenSSL的实现,可以快14倍。
同样,在 AMD Bulldozer上也有类似的指令设计。
Attacks
AES也存在比暴力搜索密钥空间更好的算法。
Best key recovery attack: four times better than ex. search [BKR’11]
Related key apack on AES-256: Given $2^{99}$ inp/out pairs from four related keys in AES-256 can recover keys in time ≈299[BK’09]
Block ciphers from PRGs
我们能否从PRG中构建PRF?
答案是:是的。
Let G: $K\rightarrow K^2$ be a secure PRG.
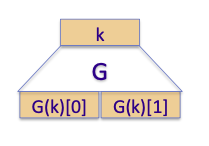
Define 1-bit PRF F: $K\times {0,1} \rightarrow K$ as
$$
F(k,x\in {0,1})=G(k)[x]
$$
根据定理,如果G是一个secure PRG,那么F就是一个secure PRF。
Thm: If G is a secure PRG then F is a secure PRF.
同样,我们可以通过这样的方式构建更大域的PRF。
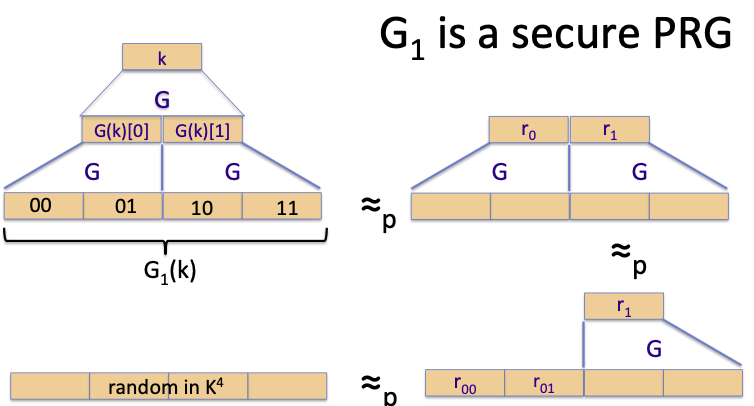
对得到的结果再做一次G运算,得到的G1就是一个2-bit PRF:
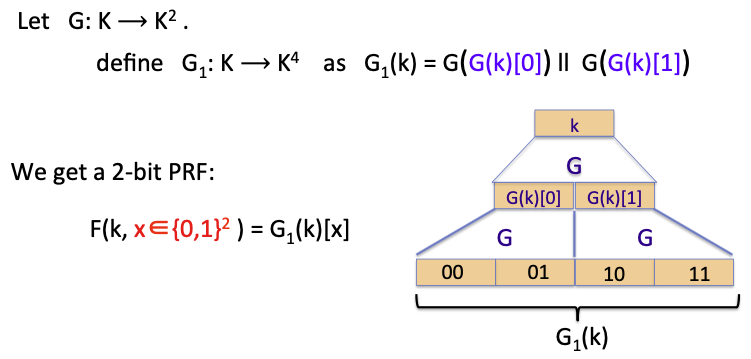
Proof: G1 is a secure PRG
证明思路就是,因为G是安全的PRG,所以k通过G运算得到的结果与随机串不可区分,同样的,最后扩展出的在 $K^4$ 中的字符串与随机串是不可区分的。
同样的,可以扩展出3-bit 的PRF,对于给定的比特输入,也是易于计算的:
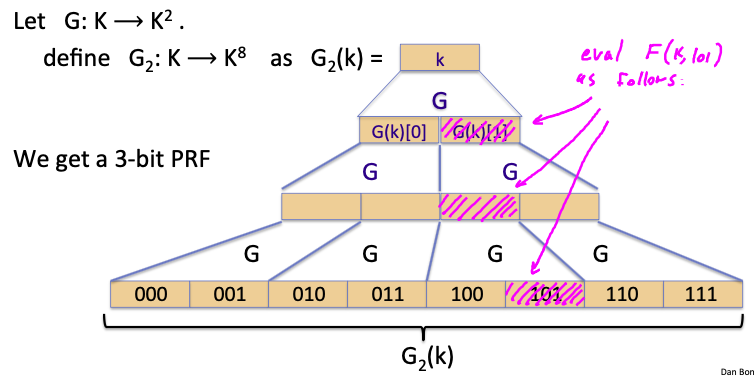
而扩展出更多bit时,就得到了GGM PRF。
GGM PRF就是通过上述的扩展方式得到 ${0,1}^n$ 域上的PRF:
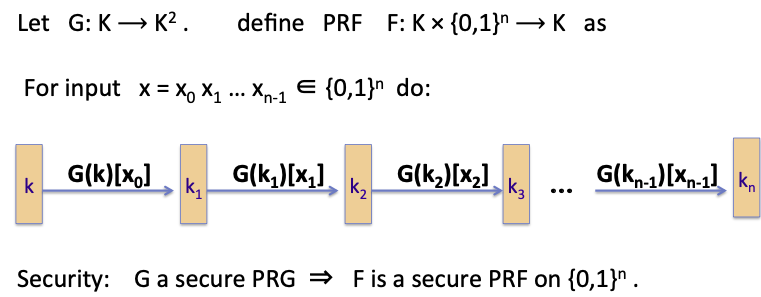
这种方式,PRF的安全性依赖于PRG的安全性。
但由于这样的方式运行效率较低,所以在实际应用中很少。
说到现在,我们好像还没有提到如何从PRG中构建块密码,因为块密码时PRPs。
如果记性比较好的读者应该还记得我们刚刚提到的Luby-Rackoff定理,将一个安全的PRF作为Feistel网络中的轮函数,3-round Feistel就可以构建一个安全的PRP,即安全的块密码。
Thm:
$f:K\times \{0,1\}^n\rightarrow \{0,1\}^n$ a secure PRFthen, 3-round Feistel $F: K^3\times{0,1}^{2n}\rightarrow {0,1}^{2n}$ a secure PRP.
「Cryptography-Boneh」:Block Cipher 1

