「Cryptography-Boneh」:Integrity

2021-11-222021-12-28 Cryptography-Boneh 31 minutes read (About 4598 words) 0 visits

这篇文章主要介绍消息验证码，即MAC (Message Auth. Code)。

文章首先介绍了secure MAC的模型和安全定义，当攻击者能伪造出新的msg/tag对时，MAC就不再安全。

文章的第二部分介绍了基于PRF的MAC构造，根据相关定理，只要PRF的输出空间足够大，且这是一个安全的PRF，则基于PRF的MAC就是安全的。

但基于PRF的MAC只能计算固定消息大小的MAC，如何利用这个工具构造出更大消息空间的MAC？

文章后半部分给出了一些主流的MAC构造：

串行构造：CBC-MAC、NMAC、CMAC
并行构造：PMAC、HMAC（下一篇文章）
基于one-time MAC: CW MAC

此外，文章还介绍了MAC Padding技术。

Message Auth. Codes

本节的目标是保证消息的完整性，暂时不考虑消息机密性。

比如保护磁盘上的公共二进制文件不会被篡改，保护web页面上的广告消息不会被替换篡改。

Def: MAC I = (S, V) defined over (K, M, T) is a pair of algs:

S(k, m) outputs t in T
V(k, m, t) outputs ‘yes’ or ‘no’

MAC是一组定义在(K, M, T)上的算法(S, V)，生成tag的算法S(k, m)和验证tag的算法V(k, m, tag)。

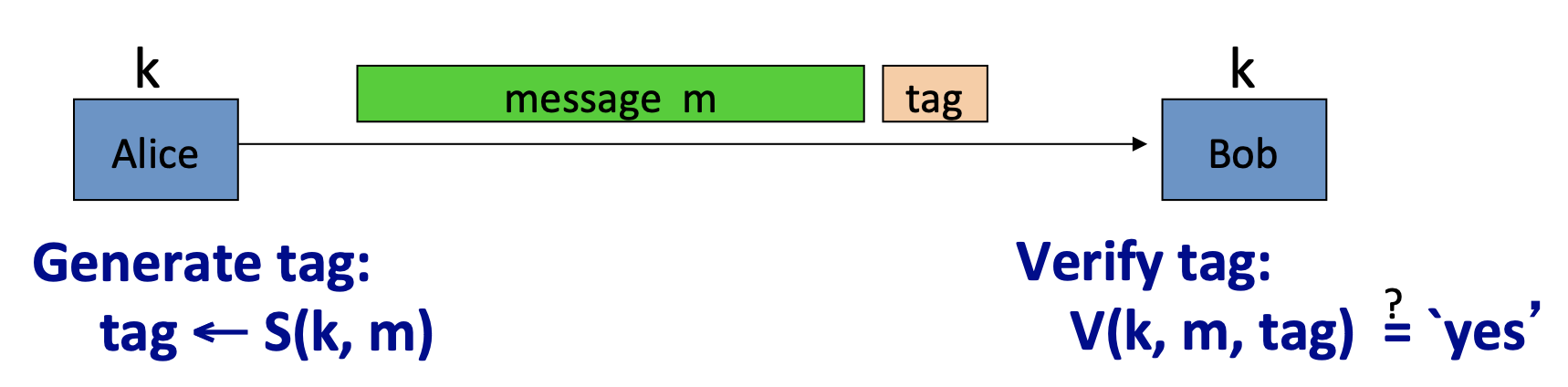
消息的完整性需要发送方和接收方共享一个密钥。

如果是用CRC来保证消息的完整性，攻击者可以修改消息，并轻易的计算出新的CRC。

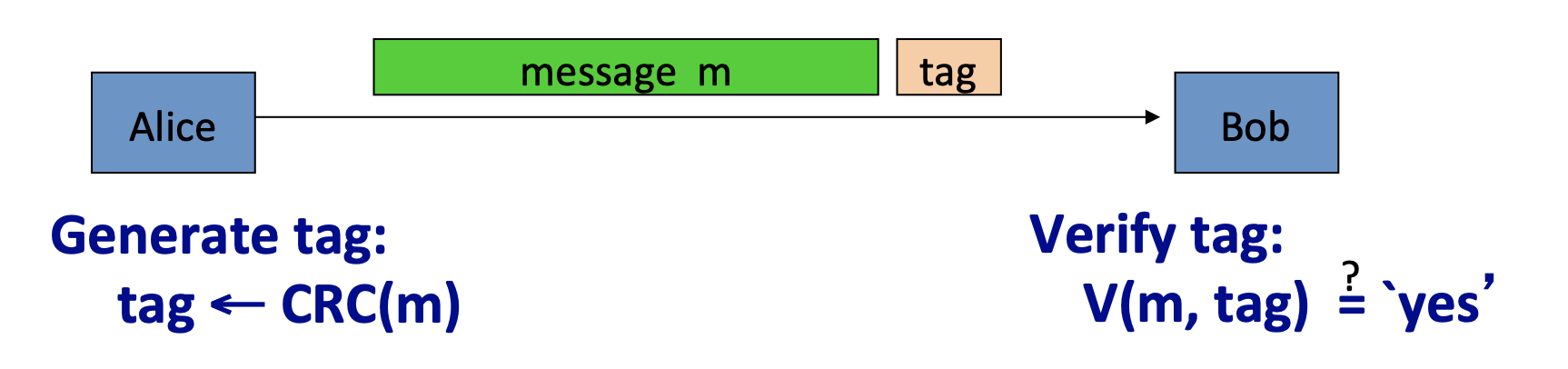
所以CRC可以用于检测随机错误（信道噪声），而不能用于检测恶意修改。

Secure MACs: Model

在定义安全MACs的模型中：

Attacker’s power: chosen message attack
选择明文攻击: 对于任意的消息 $\mathrm{m_1,m_2,…,m_q}$ ，攻击者能得到其对应的消息验证码 $\mathrm{t}_{\mathrm{i}} \leftarrow \mathrm{S}\left(\mathrm{k}, \mathrm{m}_{\mathrm{i}}\right)$
Attacker’s goal: existential forgery
伪造: 希望能伪造新的 message/tag (m,t)。
新的，意味着 $(\mathrm{m}, \mathrm{t}) \notin\left\{\left(\mathrm{m}_{1}, \mathrm{t}_{1}\right), \ldots,\left(\mathrm{m}_{\mathrm{q}}, \mathrm{t}_{\mathrm{q}}\right)\right\}$

new valid message/tag pair:

attacker cannot produce a valid tag for a new message.
意味着不能为新的消息生成有效的tag
given (m,t) attacker cannot even produce (m,t’) for $\mathrm{t’\ne t}$
也不能为原消息生成新的tag

Secure MACs: Def

在定义的MAC游戏中:

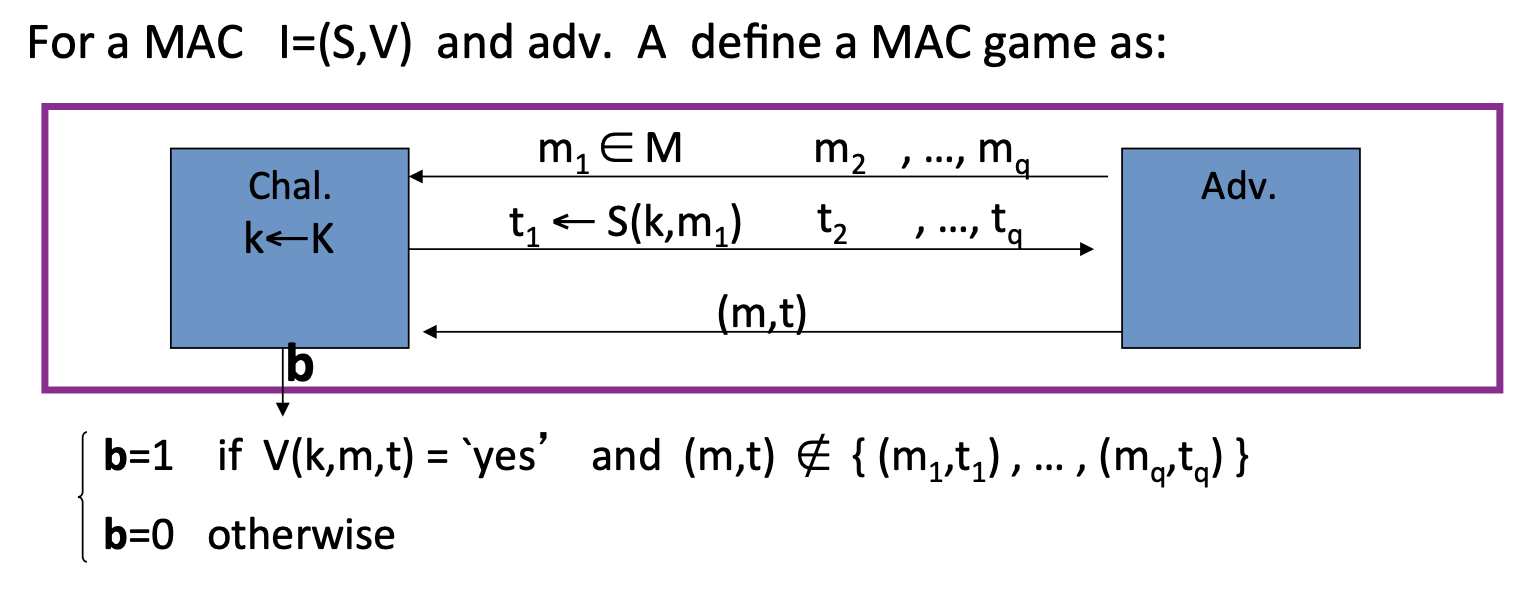
首先挑战者会随机选择密钥 $\mathrm{k\leftarrow K}$ ，作为MAC的签名算法的密钥。

攻击者向挑战者发起q个询问，每次询问都可以得到该消息对应的消息验证码。

攻击者会生成一对msg/tag pair: (m, t)，如果该pair通过了挑战者的验证算法，并且是一对新的msg/tag pair，挑战者输出：1，否则输出0。

所以secure MACs定义为：攻击者生成new message/tag pair 通过挑战者验证算法的概率为neg.

Def：I=(S, V) is a secure MAC if for all “efficient” A:
$$
\mathrm{Adv_{MAC}[A,I]=Pr[Chal. output 1]\quad is “negligible”}
$$

e.g.1:

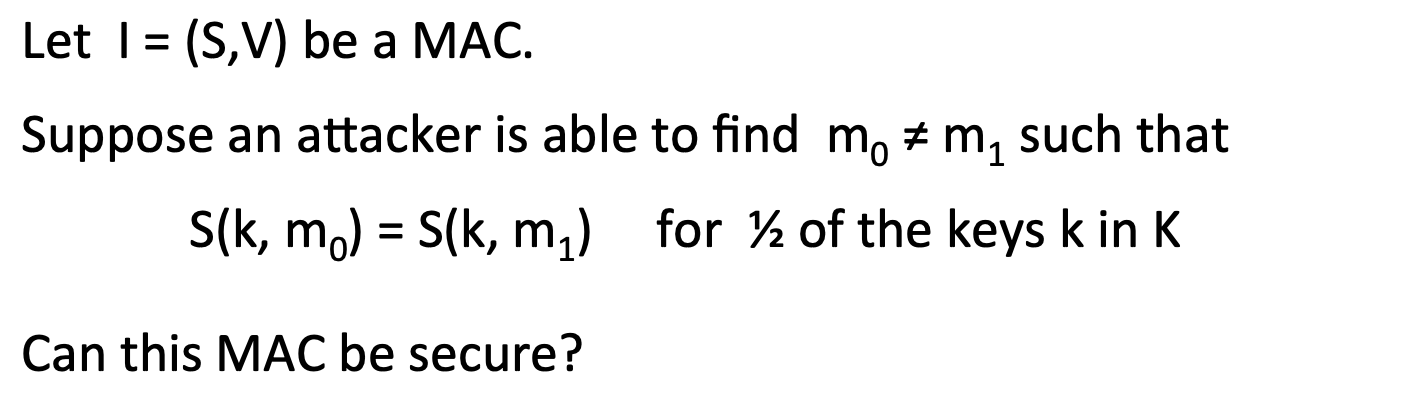
两个消息具有同样tag的概率为1/2，所以Adv[A, I]=1/2.

e.g.2:

同理，tag的长度是5bits，所以两个不同消息有同样tag的概率为1/32.

MACs Based on PRFs

任何PRF都可以转换为MAC。

对于一个PRF: $\mathrm{F:K\times X\longrightarrow Y}$

由该PRF定义的MAC $\mathrm{I_F=(S,V)}$ 为：

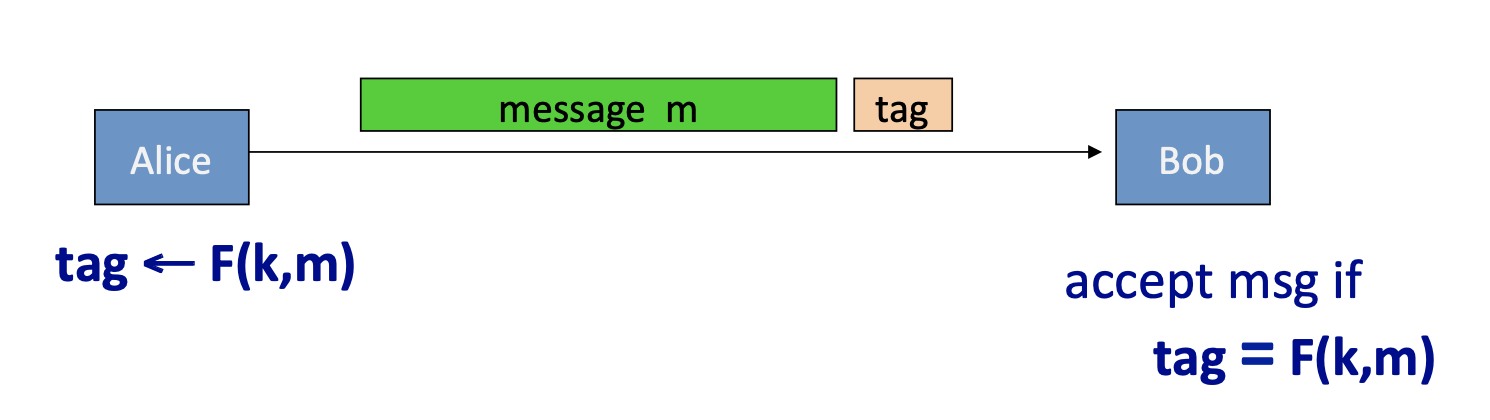
S(k, m) := F(k, m)
V(k, m, t): output ‘yes’ if t = F(k,m) and ‘no’ otherwise.

但安全的PRFs不一定可以生成安全的MACs，比如：

由上式子生成的MACs并不是一个安全的MACs，因为tag的长度太短，攻击者可以为任何消息猜测其tag。

Security

所以，要保证基于PRFs的MACs的安全性，还需要PRF的输出空间足够大，否则攻击者可以通过猜测攻击成功。

Thm:

If $\mathrm{F:K\times X\rightarrow Y}$ is a secure PRF and 1/|Y| is negligible(i.e. |Y| is large) then $\mathrm{I_F}$ is a secure MAC.

In particular, for every eff. MAC adversary A attacking $\mathrm{I_F}$ there exists an eff. PRF adversary B attacking F s.t.:
$$
\mathrm{Adv_{MAC}[A,I_F]\le Adv_{PRF}[B, F]+1/|Y|}
$$
$\mathrm{I_F}$ is secure as long as |Y| is large, say |Y| = $2^{80}$.

对于每一个攻击MAC的攻击者A，都存在攻击对应PRF的攻击者B，满足上述式子。所以如果不等式右边都为neg.，那不等式左边一定为neg.

Truncating MACs based on PRFs

Truncating MACs的定义如下：

Easy lemma: suppose $\mathrm{F:K\times X\rightarrow {0,1}}$ is a secure PRF.

Then so is $\mathrm{F_t(k,m)=F(k,m)[1\dots t]}$ for all $\mathrm{1\le t\le n}$

基于PRFs的MACs，截断后的MACs，如果tag长度足够长，也是安全的。

if (S,V) is a MAC is based on a secure PRF outputing n‐bit tags the truncated MAC outputing w bits is secure as long as $\mathrm{1/2^w}$ is still negligible (say w≥64)

Examples

AES可以看作为：a MAC for 16-byte messages.

所以引入了一个新的问题：how to convert small-MAC into a Big-MAC ?

实践中有两种主流构造方法：

CBC-MAC (banking – ANSI X9.9, X9.19, FIPS 186‐3)
HMAC (Internet protocols: SSL, IPsec, SSH, …)

Sequential Constructions

本节的主要目标是: given a PRF for short messages (AES) construct a PRF for long messages.

From here on let $\mathrm{X={0,1}^n}$ (e.g. n=128)

1. CBC-MAC

CBC-MAC 也叫 encrypted CBC-MAC (ECBC)

PRP: $\mathrm{F:K\times X\rightarrow X}$ .

ECBC定义新的PRF $\mathrm{F_{ECBC}:K^2\times X^{\le L}\rightarrow X}$ .

新的PRF的输入为：一对密钥和 long messages (L: blocks)

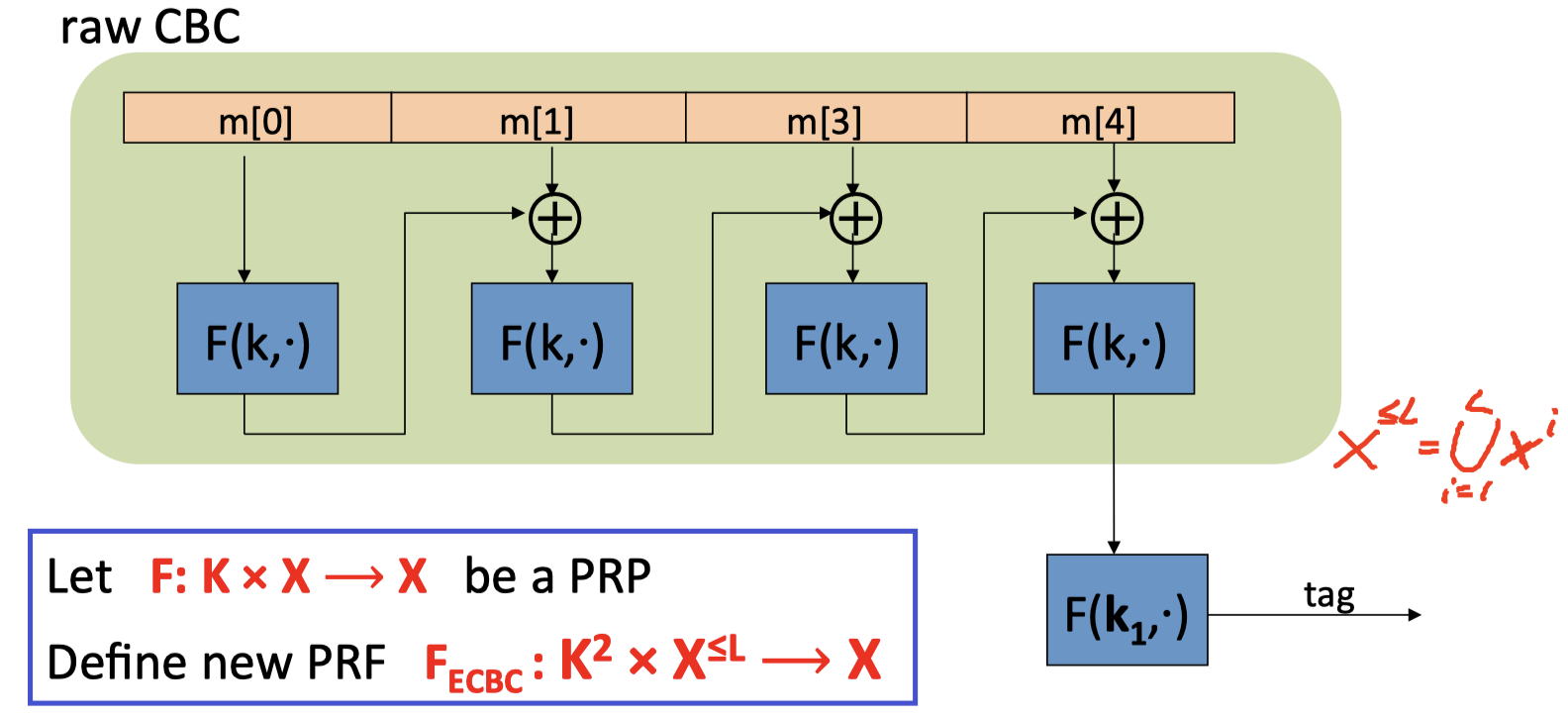
绿色部分就是原生的CBC（使用密钥k），而encrypted表现在对CBC的输出再进行加密操作（使用密钥 $\mathrm{k_1}$ ，得到消息的MAC。

需要注意的是，最后对CBC输出进行加密的密钥是独立于CBC的密钥。

2. NMAC

NMAC即 nested MAC。

PRF: $\mathrm{F:K\times X\rightarrow K}$

NMAC定义新的PRF $\mathrm{F_{NMAC}:K^2\times X^{\le L}\rightarrow K}$ .

新的PRF的输入为：一对密钥和 long messages (L: blocks)

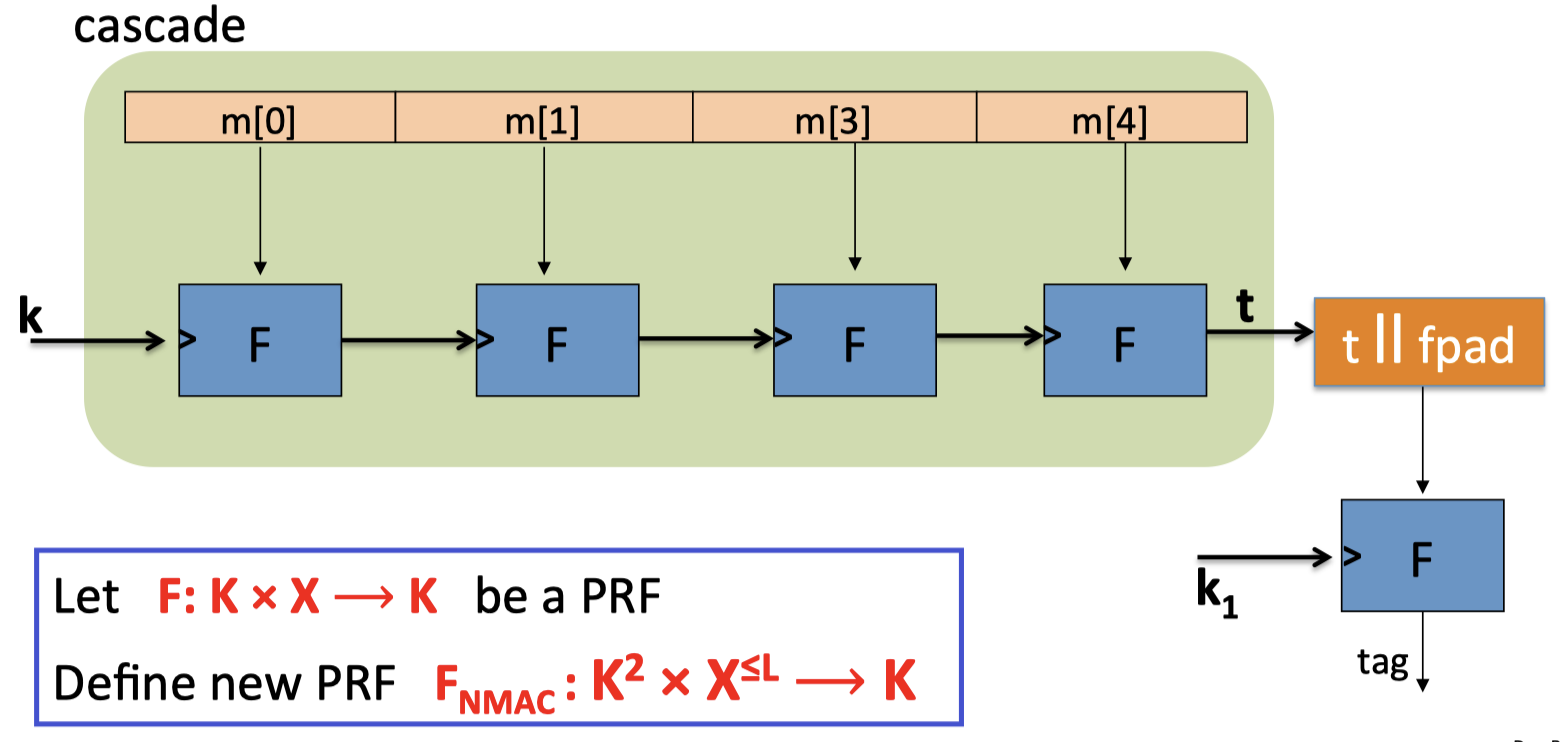
绿色部分是层叠(cascade)部分，把本次消息块PRF的输出作为下次消息块PRF运算的密钥，cascade部分的输出为t。

最后对t做padding操作（fixed pad），对于padding后的结果，用新的密钥 $\mathrm{k_1}$ 再做一次PRF运算，得到最终的MAC。

Last Encryption

在ECBC和NMAC中，最后都有加密的步骤。

Why the last encryption step in ECBC-MAC ?

NMAC:

假设NMAC只有cascade部分，即S(k,m)=cascade(k,m)

Then this MAC can be forged with one chosen msg query.

Extension Attack:

已知cascade(k, m)，对于任意消息块w，可以轻易得到cascade(k, m||w)的值。

因为cascade(k, m)是作为下一个消息块运算的密钥，所以cascade(k, m||w) = PRF(cascade(k, m), w)。

所以最后的加密步骤是为了阻止extension attack。

ECBC：

同样，假设ECBC只有raw CBC部分，没有最后加密的步骤，即S(k,m)=rawCBC(k,m).

Then $\mathrm{I_{RAW}=(S,V)}$ is easily broken using a 1-chosen msg attack.

1-chosen msg attack:

攻击者随机选择one-block message m.
请求得到m对应的tag t = F(k,m)
攻击者可以伪造2-block message $\mathrm{(m,t\oplus m)}$ 的MAC，其实也就是 t。

$\operatorname{rawCBC}(\mathrm{k},(\mathrm{m}, \mathrm{t} \oplus \mathrm{m}))=\mathrm{F}(\mathrm{k}, \mathrm{F}(\mathrm{k}, \mathrm{m}) \oplus(\mathrm{t} \oplus \mathrm{m}))=\mathrm{F}(\mathrm{k}, \mathrm{t} \oplus(\mathrm{t} \oplus \mathrm{m}))=\mathrm{t}$

Security Analysis

Theorem: For any L > 0,

For every eff. q-query PRF adv. A attacking $\mathrm{F_{ECBC}}$ or $\mathrm{F_{NMAC}}$ , there exists an eff. adversary B s.t.:

$$ \begin{array}{l}\operatorname{Adv}_{\mathrm{PRF}}\left[\mathrm{A}, \mathrm{F}_{\mathrm{ECBC}}\right] \leq \mathrm{Adv}_{\mathrm{PRP}}[\mathrm{B}, \mathrm{F}]+2 \mathrm{q}^{2} /|\mathrm{X}| \\ \operatorname{Adv}_{\mathrm{PRF}}\left[\mathrm{A}, \mathrm{F}_{\mathrm{NMAC}}\right] \leq \mathrm{q} \cdot \mathrm{L} \cdot \mathrm{Adv}_{\mathrm{PRF}}[\mathrm{B}, \mathrm{F}]+\mathrm{q}^{2} / 2|\mathrm{~K}|\end{array} $$

CBC‐MAC is secure as long as q << $|X|^{1/2}$

NMAC is secure as long as q << $|K|^{1/2}$

(q << $2^{64}$ for AES-128)

为了简化讨论，考虑不等式： $\operatorname{Adv}_{\mathrm{PRF}}\left[\mathrm{A}, \mathrm{F}_{\mathrm{ECBC}}\right] \leq \mathrm{Adv}_{\mathrm{PRP}}[\mathrm{B}, \mathrm{F}]+ \mathrm{q}^{2} /|\mathrm{X}|$

q = #messages MAC-ed with k

如果我们想得到 $\operatorname{Adv}_{\mathrm{PRF}}\left[\mathrm{A}, \mathrm{F}_{\mathrm{ECBC}}\right] \leq 1 / 2^{32}$ 的结果，必须满足： $\mathrm{q^{2} /|X|<1 / 2^{32} }$

对于基于AES的$\mathrm{F_{ECBC}}$：|X|=$2^{128}$ ，q必须满足 q < $2^{48}$ 。所以在对 $2^{48}$ 个messages进行MAC运算后，必须更换密钥。
对于基于3DES的$\mathrm{F_{ECBC}}$: |X|= $2^{64}$ ，q必须满足 q < $2^{16}$ .

Extension Property

如果构造出的PRFs(ECBC 和 NMAC)的底层PRF是一个PRP（比如AES），那么构造出的PRFs都有可扩展性：

$$ \forall \mathrm{x}, \mathrm{y}, \mathrm{w}: \mathrm{F}_{\mathrm{BIG}}(\mathrm{k}, \mathrm{x})=\mathrm{F}_{\mathrm{BIG}}(\mathrm{k}, \mathrm{y}) \quad \Rightarrow \quad \mathrm{F}_{\mathrm{BIG}}(\mathrm{k}, \mathbf{x||w} )=\mathrm{F}_{\mathrm{BIG}}(\mathrm{k}, \mathbf { y||w }) $$

因为底层是一个PRP，所以$F(k_1,\cdot)$ 是一个one to one function，输出相同，对应的输入也是相同的，因此rawCBC或者NCBC的cascade部分的输出是相同的。

The security bounds are tight: an attack

上述定理的安全约束是紧的，所以当q不满足约束时，MAC就不安全了。

After signing $|X|^{1/2}$ messages with ECBC-MAC or $|K|^{1/2}$ messages with NMAC,

the MACs become insecure.

对于满足可扩展性的PRF $\mathrm{F}_{\mathrm{BIG}}: \mathrm{K} \times \mathrm{X} \longrightarrow \mathrm{Y}$ ，可以构造出一般攻击：

随机选取 $|Y|^{1/2}$ 个不同的消息，请求询问得到对应的tag: $(m_i,t_i)$
根据生日悖论，可以找到碰撞：$t_u=t_v$
选择w，攻击者构造消息 $m_u||w$，请求询问其tag： $\mathrm{t}:=\mathrm{F}_{\mathrm{BIG}}\left(\mathrm{k}, \mathrm{m}_{\mathrm{u}} \| \mathrm{w}\right)$
此时，攻击者可以成功伪造pair： $\mathrm{(m_{v} || w, t})$
根据可扩展性， $\mathrm{t}=\mathrm{F}_{\mathrm{BIG}}\left(\mathrm{k}, \mathrm{m}_{\mathrm{v}} \| \mathrm{w}\right)$

Rand. Construction

另一种引入随机性的构造，可以具备更好的安全性。

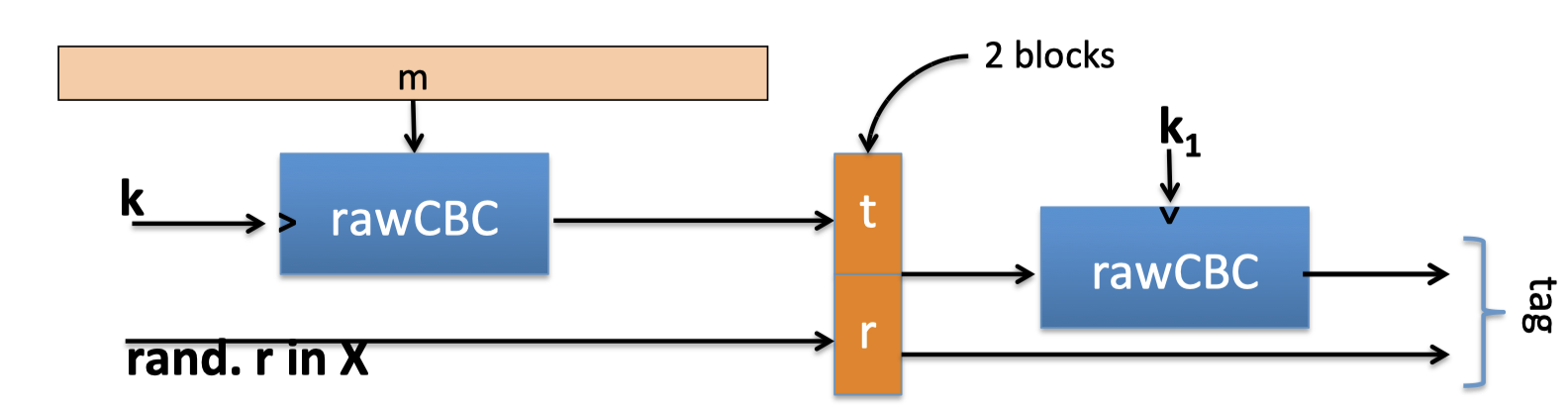
Let $\mathrm{F:K\times X\rightarrow X}$ be a PRF.

将rawCBC的结果和随机值，构造为2-block，再次进行运算。

最终的结果：MAC with tags in $X^2$

Security: $\mathrm{A d v_{M A C}\left[A, I_{R C B C}\right] \leq A d v_{P R P}[B, F] \cdot\left(1+2 q^{2} /|X|\right) }$

在这种构造情况下，3DES can sign q = $2^{32}$ msgs with one key.

Comparison

ECBC‐MAC 的构造方式常常用来构造基于AES的MAC

比如CCM encryption mode (used in 802.11i)
NIST standard called CMAC

而NMAC的构造方式一般不使用AES或3DES

主要的原因是：在NMAC中，对每个block的计算都需要更换AES密钥，也就需要重复进行AES密钥扩展。
但NMAC是HMAC的基础。

MAC Padding

如果msg的长度不是block-size的整数倍，就需要对msg进行padding操作。

CBC MAC padding

如果只是简单对msg进行0填充，那将会得到一个不安全的MAC，因为pad(m) = pad(m||0)，所以对于给定msg m 的tag，攻击者可以轻易得到m||0的tag。

因此，为了安全性的考虑，padding操作应该是可逆的，所以如果两个消息是不同的，那么进行padding操作后的消息也应该是不同的，即： $\mathrm{m}_{0} \neq \mathrm{m}_{1} \quad \Rightarrow \quad \operatorname{pad}\left(\mathrm{m}_{0}\right) \neq \operatorname{pad}\left(\mathrm{m}_{1}\right)$ ，否则攻击者就可以利用该特性进行伪造。

ISO： pad with ‘1000…00’. Add new dummy block if needed.

(The ‘1’ indicates beginning of pad)

对于msg长度不是block-size整数倍的情况，用’100..0’字符串进行填充：
对于msg长度是block-size整数倍的情况，需要增加一个dummy block:
如果不增加dummy block，padding function就不可逆了。

CMAC (NIST standard)

介绍padding后，这里介绍一种CBC-MAC的变体，也是NIST的标准。

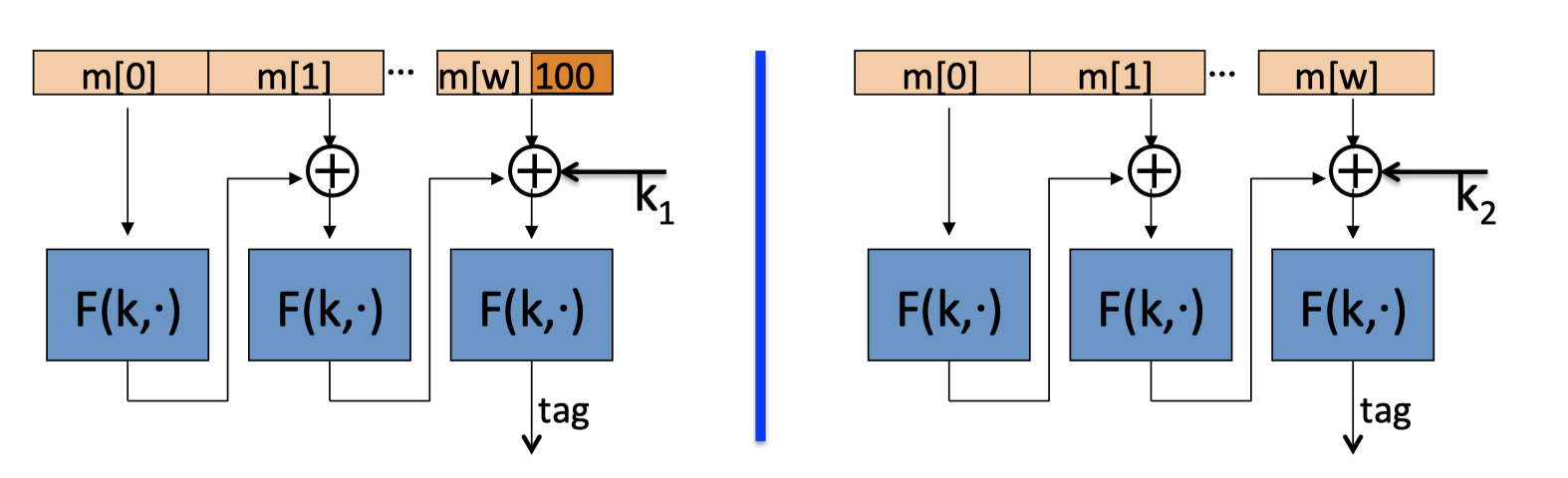
key $=(k,k_1,k_2)$

在这种构造方式下，没有最后一步的加密步骤，padding时也不需要增加dummy block。

No final encryption step (extension attack thwarted by last keyed xor)
因为最后一步使用密钥$k_2$异或，所以不知道函数F(k, ·)的输入，也就不能进行extension attack。
No dummy block (ambiguity resolved by use of $k_1$ or $k_2$)
最后一步通过两个不同密钥的使用来解决歧议情况。

Parallel Constructions

ECBC和NMAC都是时序性(sequential)，本节将通过a small PRF构造a parallel MAC.

3. PMAC: parallel MAC

Let $\mathrm{F:K\times X\rightarrow X}$ be a PRF

定义新的PRF：$\mathrm{F_{PMAC}:K^2\times X^{\le L}\rightarrow X}$ , key $=(k,k_1)$

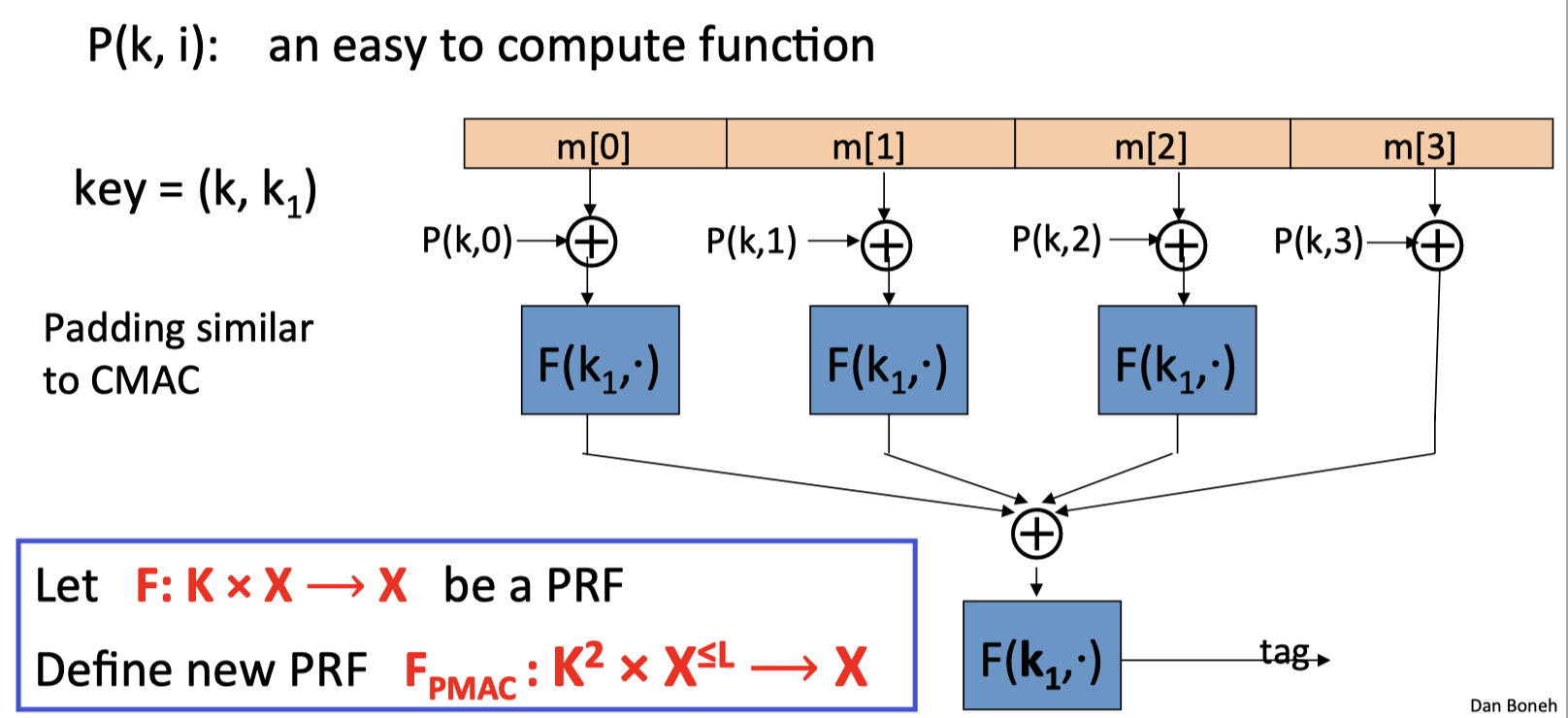
P(k, i): an easy to compute function

padding: similar to CMAC, but no need for dummy block

首先用P(k, i)对msg的每一块执行异或操作，这一步可以同步进行。异或的结果再作为$F(k_1,\cdot)$ 的输入，最后把所有$F(k_1,\cdot)$的输出异或在一起，作为最后一层$F(k_1,\cdot)$ 的输入，最终得到tag.

几点说明：

m[i] 与 P(k, i)异或的必要性：如果不进行这一步，交换消息中的不同块，也可以得到相同的MAC，即block swapping attack，PMAC变得不再安全。所以P(k, i)的作用是保存消息的顺序。
最后一块不需要再通过$F(k_1,\cdot)$，是技术原因。
因为P(k, i)增加了block的块数/顺序信息，所以不需要增加dummy block。

PMAC: Analysis

PMAC Theorem: For any L > 0,

If F is a secure PRF over (K,X,X) then $F_{PMAC}$ is a secure PRF over $\mathrm{(K,X^{\le L}, X)}$ .

For every eff. q-query PRF adv. A attacking $F_{PMAC}$, there exists an eff. PRF adversary B s.t.:
$$
\mathrm{Adv_{PRF}[A,F_{PMAC}]\le Adv_{PRF}[B,F]+2q^2L^2/|X|}
$$
PMAC is secure as long as qL << $|X|^{1/2}$ .

PMAC is incremental

PMAC是可以增量计算的。

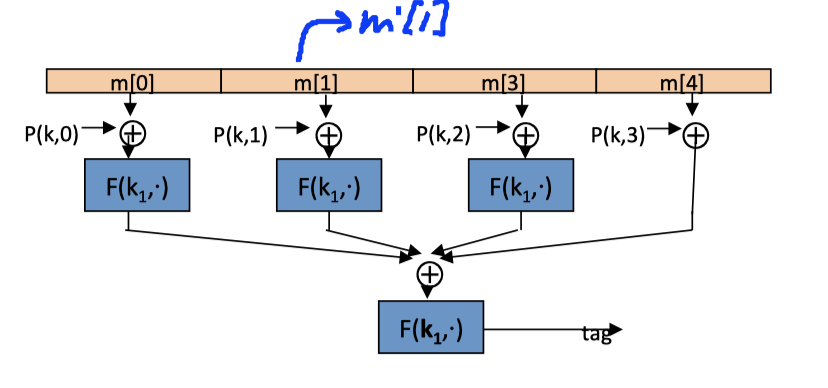
如果m[1]变成m’[1]后，可以快速更新tag = $\mathrm{F}^{-1}\left(\mathrm{k}_{1}, \mathrm{tag}\right) \oplus \mathrm{F}\left(\mathrm{k}_{1}, \mathrm{m}[1] \oplus \mathrm{P}(\mathrm{k}, 1)\right) \oplus \mathrm{F}\left(\mathrm{k}_{1}, \mathrm{m}^{\prime}[1] \oplus \mathrm{P}(\mathrm{k}, 1)\right)$

One Time MAC

One-time MAC 也是One-time pad的类比，密钥只应用于一条消息。

定义的MAC游戏如下，攻击者只能得到一条消息对应的tag：

Def: I=(S,V) is a secure MAC if for all “efficient” A:
$$
\operatorname{Adv}_{1 \mathrm{MAC}}[\mathrm{A}, \mathrm{l}]=\operatorname{Pr}[\text { Chal. outputs 1] } \quad \text { is “negligible.” }
$$

Example

One-time MAC可以抵抗所有的攻击者，具有unconditional security（perfect security）。此外，One-time MAC相对于基于PRF的MAC，具有更快的运算速度。

One-time MAC can be secure against all adversaries and faster than PRF-based MACs.

$\mathrm{q}$: 一个大素数（比如q = $2^{128}$ +51)

$\mathrm{\text {key}=(a, b) \in{1, \ldots, q}^{2}}$ : 两个随机数

$\mathrm{\mathrm{msg}=(\mathrm{m}[1], \ldots, \mathrm{m}[\mathrm{L}])}$ ：每一块都看作是是128 bit的整数

MAC ：计算以msg作为系数的多项式
$$
\begin{array}{c}S(\text { key, msg} )=\mathrm{P_{m s g}(a)+b \quad(\bmod q)} \ \text { where } \mathrm{P_{m s g}(x)=x^{L+1}+m[L] \cdot x^{L}+\ldots+m[1] \cdot x \quad \text { is a poly. of } \operatorname{deg} L+1 }\end{array}
$$
We show: given S( key, $\mathrm{msg_1}$ ) adv. has no info about S( key, $\mathrm{msg_2}$ )

在One- time MAC中，S(key, $\mathrm{msg_1}$ )不会透露任何关于S(key, $\mathrm{msg_2}$)的信息，所以One-time key是绝对安全的，但和ont-time pad 类似，如果将相同密钥作用于不同的消息上，two-time MAC则是不安全的。

Unconditional Security

在上面的例子中：given S( key, $\mathrm{msg_1}$ ) adv. has no info about S( key, $\mathrm{msg_2}$ )，现在我们来证明one-time MAC的unconditional security.

Thm: the ont-time MAC in the example satisfies: (L = msg-len, q is the prime)
$$
\mathrm{\forall m_{1} \neq m_{2}, t_{1}, t_{2}: \quad P r_{a, b}\left[s\left((a, b), m_{1}\right)=t_{1} \mid s\left((a, b), m_{2}\right)=t_{2}\right] \leq L / q}
$$
Proof: $\forall \mathrm{m_1\ne m_2,t_1,t_2}:$

$\mathrm{\operatorname{Pr}_{a, b}\left[s\left((a, b), m_{2}\right)=t_{2}\right]=\operatorname{Pr}_{a, b}\left[P_{m_{2}}(a)+b=t_{2}\right]=1 / q}$ 对于任意的$m_2$，多项式计算出的结果等于$t_2$ 的概率为1/q。
$\mathrm{\operatorname{Pr}_{\mathrm{a}, \mathrm{b}}\left[s\left((\mathrm{a}, \mathrm{b}), \mathrm{m}_{1}\right)=\mathrm{t}_{1} \text { and } s\left((\mathrm{a}, \mathrm{b}), \mathrm{m}_{2}\right)=\mathrm{t}_{2}\right]}$ $=\operatorname{Pr}_{\mathrm{a}, \mathrm{b}}\left[\mathrm{P}_{\mathrm{m}_{1}}(\mathrm{a})-\mathrm{P}_{\mathrm{m}_{2}}(\mathrm{a})=\mathrm{t}_{1}-\mathrm{t}_{2} \text { and } \mathrm{P}_{\mathrm{m}_{2}}(\mathrm{a})+\mathrm{b}=\mathrm{t}_{2}\right] \leq \mathrm{L} / \mathrm{q}^{2}$
- 概率第二个条件，任意的$m_2$，多项式计算出的结果等于$t_2$ 的概率为1/q。
- 概率第一个条件，两式相减后，得到一个deg L的多项式，该多项式值为 $\mathrm{t_1-t_2}$ 的概率为1/q。但这是一个度为L的多项式，所以最多可能有L个根。所以第一个条件的概率是<=L/q
最后使用条件概率

该定理表明，只得到一对有效的 $(m_2,t_2)$，攻击者构造出有效 $(m_1,t_1)$ 的概率 $\le \mathrm{L/q}$ .

Many-time MAC: Cater-Wegman MAC

(S,V): 是一个安全的one-time MAC over $(K_I,M,{0,1} ^n)$.

$F:K_F\times {0,1}^n \rightarrow {0,1}^n$ 是安全的PRF.

Cater-Wegman MAC:
$$
\mathrm{C W\left(\left(k_{1}, k_{2}\right), m\right)=\left(r, F\left(k_{1}, r\right) \oplus S\left(k_{2}, m\right)\right)} \quad \text{ for random r }\leftarrow {0,1}^n
$$
CW MAC首先选取了一个随机值 r，然后用PRF对随机值加密,，得到 $\mathrm{F(k_1,r)}$ 。再用one-time MAC作用于消息，得到的结果与PRF的结果异或。

这也是一个randomized MAC，当计算不同消息验证码时，密钥可以重复使用，但每次都选取不同的随机值。PRF计算较慢，但作用在一个较短的随机串上，one-time MAC计算更快。作用在较长的消息串上，Carter-Wegman MAC更适合。

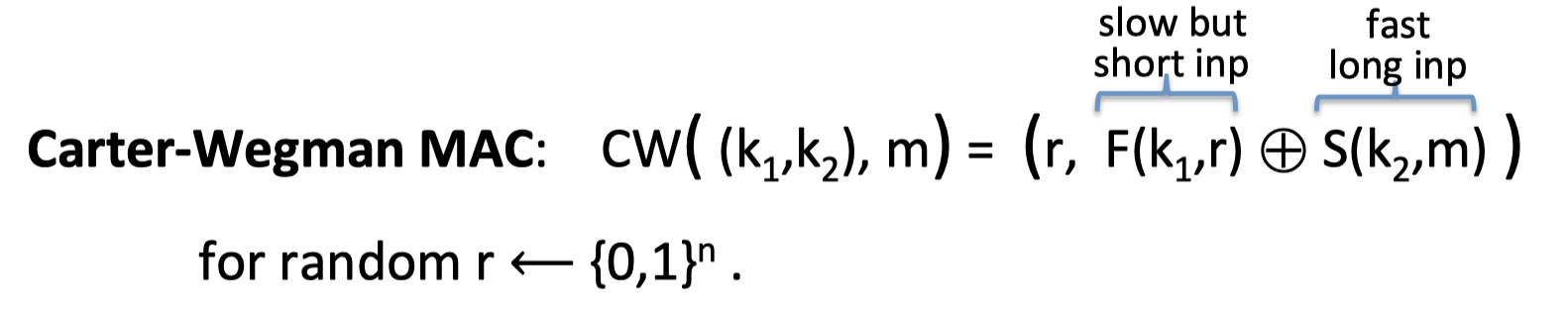
Thm : If (S,V) is a secure one-time MAC and F is a secure PRF, then CW is a secure MAC outputting tags in ${0,1}^{2n}$ .