「Cryptography-MIT6875」: Lecture 2
Science wins either way.
Topics:
- How to circumvent Shannon’s lower bound: the computational adversary
- Definition of computational security
- The definition of pseudorandom generators(PRG)
Recap
In the previous blog, we define two equivalent definitions of security, Perfect Secrecy and Perfect Indistinguishability, with the setting of an arbitrary computationally unbounded adversary.
- Perfect Secrecy: A posteriori = A priori
For all $m, c$: $\operatorname{Pr}[\mathcal{M}=m\mid \operatorname{E}(\mathcal{K,M)}=c] = \operatorname{Pr}[\mathcal{M}=m]$ - Perfect Indistinguishability:
For all $m_0, m_1, c$: $\operatorname{Pr}[ \operatorname{E}(\mathcal{K,m_0)}=c] = \operatorname{Pr}[\operatorname{E}(\mathcal{K,m_1)}=c]$
Although the definitions above are equivalent, sometime one is more convenient to work with than the other.
We mentioned that the perfect secrecy is achievable using one-time pad. However, the keys are as long as messages in one-time pad.
Worse still, in Shannon’s theorem, for any perfectly secure scheme, the key space must be larger than or equal to the message space, i.e. $\mathcal{|K|\ge|M|}$.
This is known as Shannon’s conundrum.
Therefore, the gist of this blog is how we can overcome Shannon’s conundrum.
Computational Security
Before that, I’ll introduce two mathematical definitions to instantiate Perfect Indistinguishability.
Perfect Indistinguishability
As mentioned in the previous blog, Perfect Indistinguishability is substantially a formalization of the Turing test.

There are two worlds, world 0 and world 1. The two worlds both sample the key $k$ from the key space $\mathcal{K}$, and the world 0 uses $k$ to encrypt $m$ while world 1 uses $k$ to encrypt $m’$.
The adversary called EVE is a distinguisher that gets the $c$ and tries to guess which world she’s in.
Perfect Indistinguishability:
For all $m_0, m_1, c$: $\operatorname{Pr}[ \operatorname{E}(\mathcal{K,m_0)}=c] = \operatorname{Pr}[\operatorname{E}(\mathcal{K,m_1)}=c]$There are two mathematical definitions to instantiate Perfect Indistinguishability.
The First Def:
The probability that EVE think she is in World 0 is the same.
$\begin{array}{l}\text{For all EVE and all }m_0, m_1:\\ \operatorname{Pr}[k\leftarrow \mathcal{K}; c=E(k,m_0):\mathrm{EVE}(c)=0] = \operatorname{Pr}[k\leftarrow \mathcal{K}; c=E(k,m_1):\mathrm{EVE}(c)=0]\end{array}$The Second Def:
The probability of EVE guessing correctly which world she is in is exactly half.
$\begin{array}{l}\text{For all EVE and all }m_0, m_1:\\ \operatorname{Pr}[k\leftarrow \mathcal{K}; b\leftarrow \{0,1\};c=E(k,m_b):\mathrm{EVE}(c)=b] = 1/2\end{array}$Key Idea: Computationally Bounded Adversaries
Now, back to the question of how to overcome Shannon’s conundrum.
The key idea is we relax the adversary to an arbitrary computationally bounded adversary.
Computational Indistinguishability (take 1)
In order to define the computationally bounded adversary (or, Computational Indistinguishability), I’ll introduce the axiom of modern crypto that Feasible Computation = Probabilistic Polynomial-time.
The Axiom of Modern Crypto: p.p.t
Feasible Computation = Probabilistic polynomial-time
- p.p.t. is the abbreviation for Probabilistic Polynomial-time
- It’s a polynomial in a security parameter n (in next subsection).
So, in the scenario of Secure Communication mentioned above, Alice and Bob are fixed p.p.t. algorithms while Eve is any p.p.t. algorithm.
Toy Definition with p.p.t.
Let’s attempt to define Computational Indistinguishability with p.p.t..
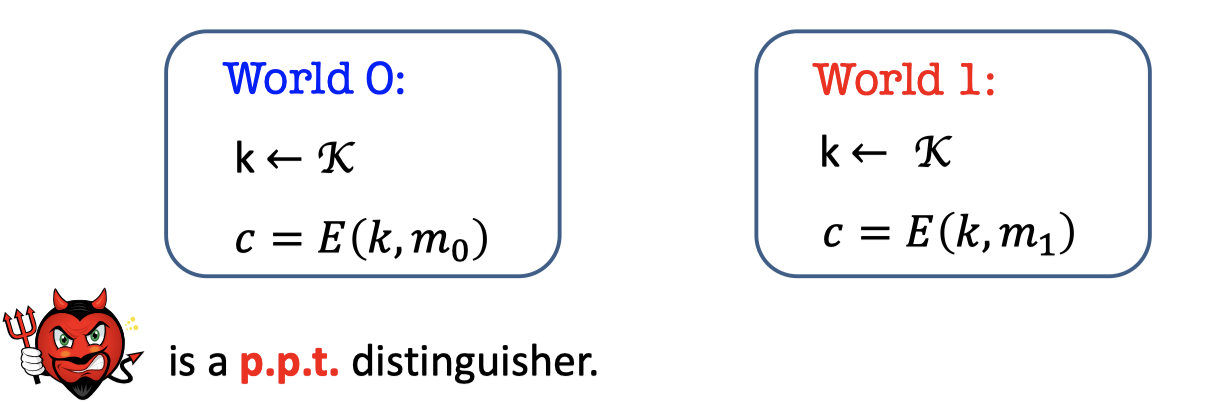
There are two worlds again, world 0 and world 1.The only difference from the unbounded case is that the adversary is a p.p.t. distinguisher.
Write it as a mathematical definition.
Toy Def:
$\begin{array}{l}\text{For all p.p.t EVE and all }m_0, m_1:\\ \operatorname{Pr}[k\leftarrow \mathcal{K}; c=E(k,m_0):\mathrm{EVE}(c)=0] = \operatorname{Pr}[k\leftarrow \mathcal{K}; c=E(k,m_1):\mathrm{EVE}(c)=0]\end{array}$Not Feasible
However, it’s still subject to Shannon’s impossibility which means the key space must be larger than or equal to the message space for any scheme s.t. the Toy Def.
Prove it by contradiction same with the proof of Shannon’s Theorem.
Proof:
Assume the contradiction that the key is n bits and the message is n+1 bits, i.e. $\mathcal{|K|<|M|}$.
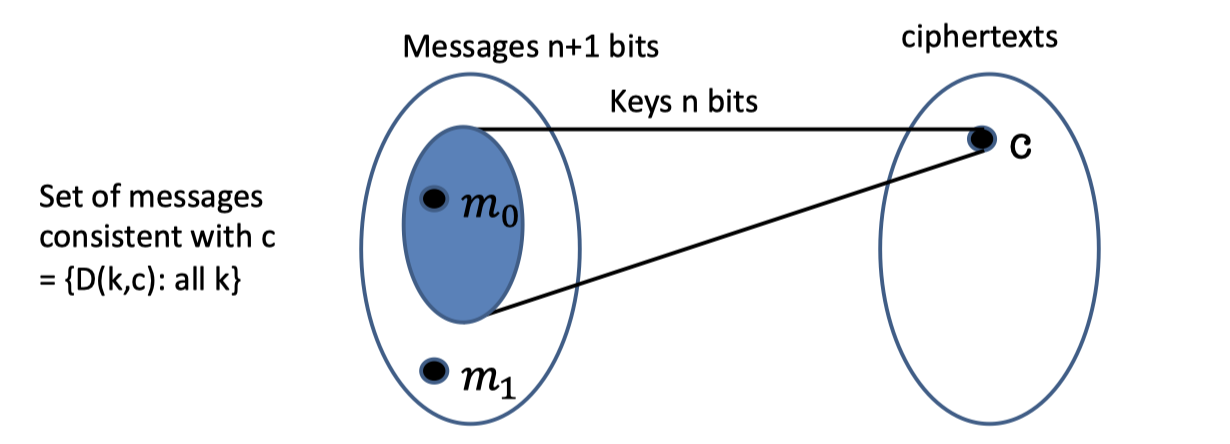
If we pick any $c\in \mathcal{C}$ and decrypt $c$ with all distinct keys, there are at most $|\mathcal{K}|$ possible messages.
The possible message space is the blue part in the left ellipse which the size is at most $|\mathcal{K}|$ and less than $\mathcal{|M|}$.Assume $m_0$ is inside the possible message space (inside the blue part) while $m_1$ is outside the possible message space.
Consider Eve that picks a random key k and
- output 0 if $\mathrm{D}(k,c)=m_0$ (w.p $\ge 1/2^n$)
It’s possible because $m_0$ is inside the blue part. - output 1 if $\mathrm{D}(k,c)=m_1$ (w.p $=0$)
It’s impossible. - output a random bit if neither holds. (w.p $=1/2$)
- output 0 if $\mathrm{D}(k,c)=m_0$ (w.p $\ge 1/2^n$)
Hence, the probability of EVE guessing correctly which world she is in is more than half.
$\begin{array}{l}\text{There exist EVE and }m_0, m_1:\\ \operatorname{Pr}[k\leftarrow \mathcal{K}; b\leftarrow \{0,1\};c=E(k,m_b):\mathrm{EVE}(c)=b] = 1/2 + 1/2^n\end{array}$
Computational Indistinguishability (take 2)
For the purpose of circumventing the Shannon’s lower bound, I’ll introduce a new notion.
Negligible Functions
Informally, Negligible Functions are functions that grow slower than $1/p(n)$ for any polynomial $p$.
Definition of Negligible Functions:
A function $\mu :\mathbb{N} \rightarrow \mathbb{R}$ is negligible if for every polynomial function $p$, there exists an $n_0$ s.t.
for all $n>n_0$:
$$
\mu(n) < 1/p(n)
$$
The key property of negligible function is that events that occur with negligible probability look to poly-time algorithms like they never occur.
Examples:
Is $\mu$ negligible ?
- $\mu(n)=1/n^{100}$ if $n$ is prime.
No, choose $p(n)=n^{200}$.- $\mu(n)=1/2^n$
Yes.
Let $\mu(n)$ be a negligible function and $q(n)$ a polynomial function.
Then $\mu(n)q(n)$ is negligible function. ( Run the event $q(n)$ times)
Security Parameter: n
Security Parameter $n$ (sometimes $\lambda$) always appears in papers.
What the hell is it ?
Security Parameter is used to measure how secure your system is.
Security Parameter is sort of an input to all these algorithms to instantiate them.
So runtimes & success probabilities are measured as a function of $n$.
- We want honest parties run in time (fixed) polynomial in $n$.
- We want adversaries run in time (arbitrary) polynomial in $n$, and should have success probability negligible in $n$.
Definition
Now we can define Computational Indistinguishability with p.p.t and negligible function.
Definition:
$ \begin{array}{l}\text { For all p.p.t EVE, there is a negligible function } \mu \text { s.t. for all } m_{0}, m_{1}: \\ \operatorname{Pr}\left[k \leftarrow \mathcal{K} ; b \leftarrow\{0,1\} ; c=E\left(k, m_{b}\right): \operatorname{EVE}(c)=b\right] \leq 1 / 2+\mu(n)\end{array} $Hence, the probability of EVE guessing correctly which world she is in is substantially half, which is half plus a negligible function of security parameter.
Pseudorandom Generators (PRG)
In the section, I’ll introduce our first crypto tool: Pseudorandom Generators (PRG).
Before that, I want to ask a question. Can you take 10 random bits as input and deterministically generate 20 bits of randomness as output ?
No, you cannot generate randomness out of nothing.
Informally, Pseudo-random Generators are deterministic programs that stretch a “truly random” seed into a (much) longer sequence of “seeming random” bits.
There are more questions after having the informal definition.
How to define “seeming random” ? Can such a G exist ?
3 Equiv. Definitions of PRG
For the first question that how to define a strong pseudo-random number generator, there are three equivalent definitions.
Def 1 [Indistinguishability]
“No polynomial-time algorithm can distinguish between the output of a PRG on a random seed vs. a truly random string.”
= “as good as” a truly random string for all practical purpose.
Def 2 [Next-bit Unpredictability]
“No polynomial-time algorithm can predict the (i+1)th bit of the output of a PRG given the first i bits, better than chance 1/2.”
Def 3 [Incompressibility]
“No polynomial-time algorithm can compress the output of the PRG into a shorter string”
All three definitions are equivalent!
In this blog, I’ll just elaborate[*详尽说明; explain] the first definition of indistinguishability.
The other two definitions and the proof will be elaborated in following blog.
Def 1: Indistinguishability
Def 1 [Indistinguishability]
A deterministic polynomial-time computable function ${G}:\{0,1\}^n\rightarrow \{0,1\}^m$ is a PRG if:
- It is expanding: $m>n$ and
- for every p.p.t. algorithm D (called a distinguisher or a statistical test) if there is a negligible function ${\mu}$ such that: $$ |\operatorname{Pr}[D({G(U_n)})=1]-\operatorname{Pr}[D({U_m})=1]|={\mu(n)} $$ Notation: $U_n$(resp. $U_m$) denotes the random distribution on $n$-bit (resp. $m$-bit) strings; $m$ is shorthand for $m(n)$.
First of all, PRG is a deterministic polynomial-time computable function which can expand $n$ bits to $m$ bits. $m$ is shorthand for $m(n$) and $m>n$.
There are two worlds, world 1 and world 2.
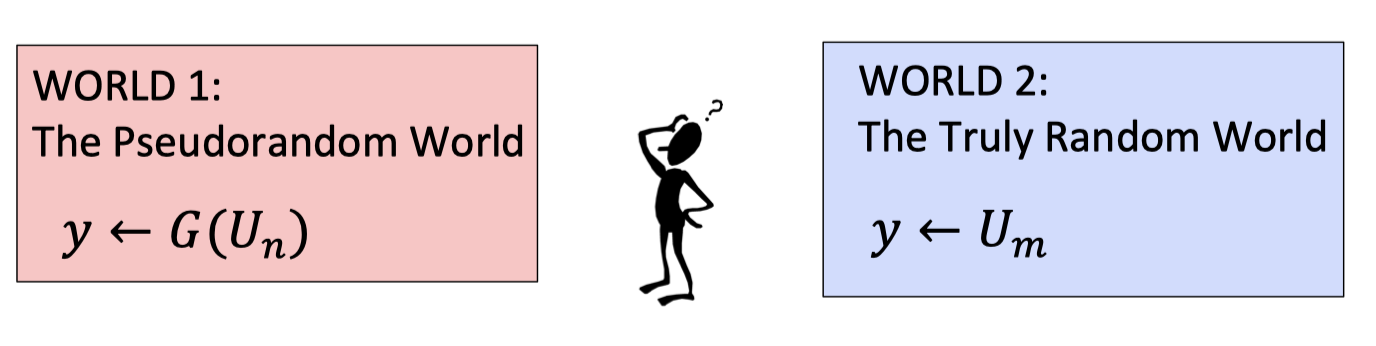
World 1 is the pseudorandom world which samples a truly random $n$-bit string from $U_n$ and expands it to a $m$-bit string using PRG $G$, and output the expanded $m$-bit string as $y$.
World 0 is the truly random world which sample a truly random $m$-bit string from $U_m$, and output the sampled $m$-bit string as $y$.
The adversary is a p.p.t distinguisher that gets the $y$ and tries to tell which world she’s in.
Why good ?
Why is this a good definition ?
It’s good for all applications. As long as we can find truly random seeds, can replace true randomness by the output of PRG(seed) in any (polynomial-time) application.
If the application behaves differently, then it constitutes a (polynomial-time) statistical test between PRG(seed) and a truly random strings.
PRG can Overcome Shannon’s Conundrum
PRG can overcome Shannon’s conundrum. That is, we can encrypt $n+1$ bits using an $n$-bit key.
How to achieve it ?
The scheme consists of three algorithms.
- $Gen(1^n)$: generate a random n-bit key $k$
- $Enc(k,m)$ where $m$ is a $m(n)$-bit message:
- Expand $k$ into a $(n+1)$-bit pseudorandom string $k’=G(k)$
- One time pad with $k’$: $c = k’\oplus m$
- $Dec(k, c)$: output $G(k)\oplus c$
$G$ is a public and deterministic p.p.t. function, so Alice and Bob can both calculate the one-time pad key $k’=G(k)$.
Correctness:
$Dec(k,c)=G(k)\oplus c = G(k)\oplus G(k)\oplus m = m$
The correctness is easily proved.
The scheme is under the assumption that $G$ is a pseudorandom generator.
Hence, if there exists a PRG, we can move beyond Shannon’s.
Security Analysis
The most important thing is to prove the scheme is computational secure.
Recall the definitions of computational indistinguishability and pseudorandom generator.
Def of Computational Indistinguishability:
$\begin{array}{l}\text{For all {p.p.t} EVE, {there is a negligible function} }{\mu }\\ \text{s.t. for all } m_0, m_1:\\ \operatorname{Pr}[k\leftarrow \mathcal{K}; b\leftarrow \{0,1\};c=E(k,m_b):\mathrm{EVE}(c)=b] \le 1/2 + \mu(n)\end{array}$Def of PRG [Indistinguishability]:
A deterministic polynomial-time computable function ${G}:\{0,1\}^n\rightarrow \{0,1\}^m$ is a PRG if:
$\begin{array}{l}\text{For all {p.p.t} EVE, {there is a negligible function} }{\mu }\text{ s.t. for all } m_0, m_1:\\ |\operatorname{Pr}[D({G(U_n)})=1]-\operatorname{Pr}[D({U_m})=1]|={\mu(n)}\quad ,m>n\end{array}$The following proof is maybe your first reduction.
The scheme is under the assumption that $G$ is a pseudorandom generator.
Hence, the thing we want to prove is if $G$ is a pseudorandom generator, then the scheme is computational secure.
Proof:
We want to prove the contradiction for simplicity that if the scheme doesn’t satisfy the computational indistinguishability, then the assumption doesn’t hold, i.e. $G$ is not a PRG.
Suppose for contradiction that there is a p.p.t. $\operatorname{EVE}$, a polynomial function $p$ and $m_0, m_1$ s.t.
$\operatorname{Pr}[k\leftarrow \mathcal{K}; b\leftarrow \{0,1\};c=Enc(k,m_b):\mathrm{EVE}(c)=b] \ge 1/2 + p(n)$Case 1: If $\operatorname{EVE}$ is a distinguisher for the scheme, instantiate it.
- $\rho = \operatorname{Pr}[k\leftarrow \{0,1\}^n; b\leftarrow \{0,1\};c=G(k)\oplus m_b:\mathrm{EVE}(c)=b] \ge 1/2 + p(n)$
- The probability of $\operatorname{EVE}$ guessing correctly which world she is in is more than half.
- As a result, $\operatorname{EVE}$ is able to distinguish case 1.
Case 2: If EVE is a distinguisher for one-time pad, instantiate it.
- $\rho' = \operatorname{Pr}[k'\leftarrow \{0,1\}^{n+1}; b\leftarrow \{0,1\};c=k'\oplus m_b:\mathrm{EVE}(c)=b] = 1/2 \;(+\mu(n))$
- The probability of $\operatorname{EVE}$ guessing correctly which world she is in is substantially half.
- As a result, $\operatorname{EVE}$ cannot distinguish case 2.
Then we can construct a distinguisher $\operatorname{EVE’}$ for $G$ using distinguisher $\operatorname{EVE}$.
- A distinguisher for PRG is to get $y$ and try to tell whether $y$ is from the pseudorandom world and the truly random world.
- Construct $\operatorname{EVE}’$:
Get as input a string $y$, run $\operatorname{EVE}(y\oplus m_b)$ for a random $b$, and let $\operatorname{EVE}$’s output be $b’$. Output “PRG” if $b=b’$ and “RANDOM” otherwise.- Run $\operatorname{EVE}(y\oplus m_b)$ for a random $b$
- Let $b’:=\operatorname{EVE}(y\oplus m_b)$
- $\operatorname{EVE}'(y)=\begin{cases} \text{PRG},& b=b'\\ \text{RANDOM},& \text{otherwise}\end{cases}$
- If $y$ is from the pseudorandom world,
- $\operatorname{EVE}$ is trying to distinguish the Case 1 when running $\operatorname{EVE}(y\oplus m_b)$ for a random $b$.
- The probability of $\operatorname{EVE}(y\oplus m_b)$ guessing $b$ correctly, i.e. $b’=b$, is more than half.
- $\operatorname{Pr}[\operatorname{EVE’}\text{ outputs PRG}\mid y\text{ is pseudorandom}]=\rho \ge 1/2 + 1/p(n)$
- If $y$ is from the truly random world,
- $\operatorname{EVE}$ is trying to distinguish the Case 2 when running $\operatorname{EVE}(y\oplus m_b)$ for a random $b$.
- The probability of $\operatorname{EVE}(y\oplus m_b)$ guessing $b$ correctly, i.e. $b’=b$, is substantially half.
- $\operatorname{Pr}[\operatorname{EVE’}\text{ outputs RANDOM}\mid y\text{ is random}]=\rho’ = 1/2$
Hence, the advantage of $\operatorname{EVE}’$ distinguishing for $G$ is $\operatorname{Pr}[\operatorname{EVE'}\text{ outputs PRG}\mid y\text{ is pseudorandom}]-\operatorname{Pr}[\operatorname{EVE'}\text{ outputs RANDOM}\mid y\text{ is random}]\ge 1/p(n)$ , which proves $G$ is not a PRG.
QED.
So far we have proven it that $G$ is not a PRG if the scheme is not (computational) secure which also means the scheme is (computational) secure if there exists a PRG $G$.
We make a reduction from whether the scheme is (computational) secure to whether PRGs exist. It’s a simple but typical reduction. The reductions will be more intricate but the principle remains same.
Two Questions to PRG
As a consequence, the proof of security comes back to PRGs.
There are two questions to PRGs
- Q1: Do PRGs exist ?
- Q2: How do we encrypt longer messages or many messages with a fixed key ?
The next subsection will answer the first question Q1 while Q2 will be answered in following blog.
Q1: Do PRGs Exist ?
Do PRGs exist ?
If P=NP, PRGs do not exist.
I believe P$\ne$NP so I believe PRGs do exist.
There are two methodologies to construct PRGs, the practical methodology and the foundational mehodology.
Rigndael (AES) is designed by the practical methodology, but this course is more about the foundational methodology.
The Practical Methodology
Start from a design framework.
A practical truth is appropriately chosen functions composed appropriately many times look random. For example, if you repeat the knot many and many times, then you will get a random line ball.
Come up with a candidate construction.
e.g. the construction of Rijndael (AES) .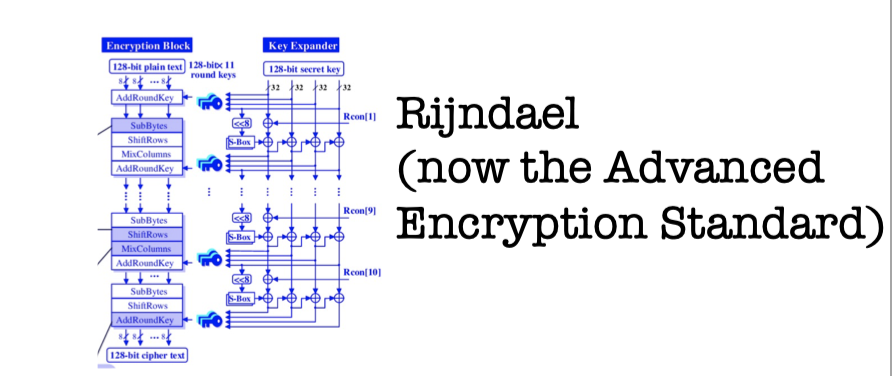
Do extensive cryptanalysis.
The Foundational Methodology
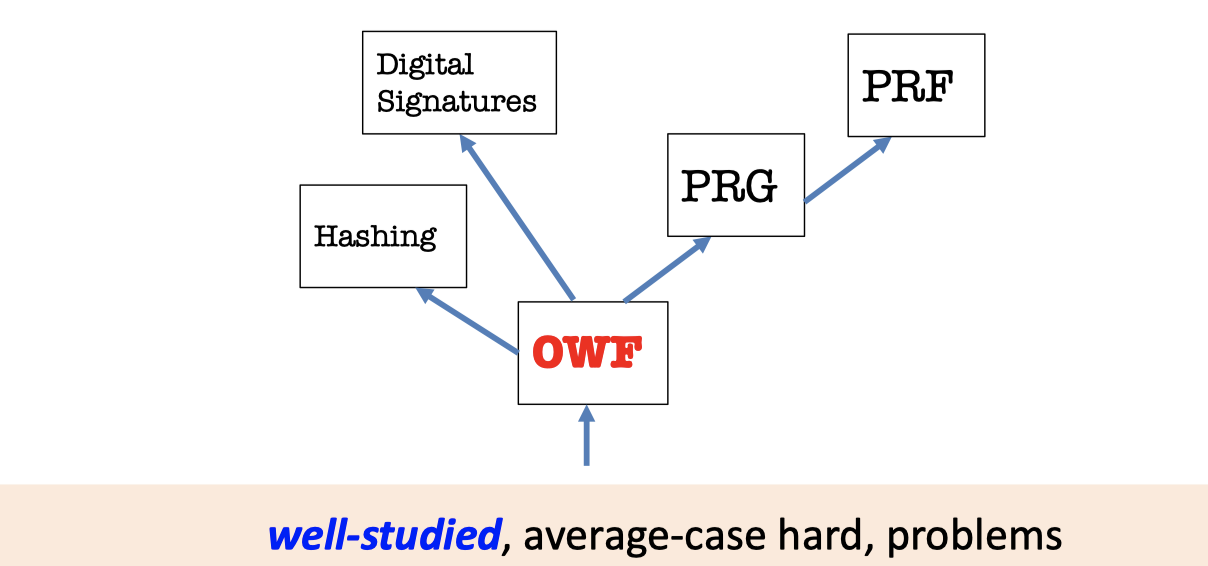
The maxim is reducing to simpler primitives.
Construct one-way function (OWF) from well-studied and average-case hard problems.
Then create the thriving world of cryptography based on OWF.
“Science wins either way” ——Silvio Micali
There is a PRG candidate from the average-case hardness of subset-sum.
A PRG Candidate from the average-case hardness of Subset-sum:
$G(a_1,\dots,a_n,x_1,\dots,x_n)=(a_1,\dots,a_n,\sum_{i=1}^n x_i a_i \mod{2^{n+1}})$
where $a_i$ are random $(n+1)$-bit numbers, and $x_i$ are random bits.
Nevertheless, there exists a better way to construct PRG.
Beautiful Function:
If $G$ is one-way function, then $G$ is a PRG.
If lattice problems are hard on the worst-case, $G$ is a PRG.
「Cryptography-MIT6875」: Lecture 2

