「Cryptography-MIT6875」: Lecture 9

In this series, I will learn MIT 6.875, Foundations of Cryptography, lectured by Vinod Vaikuntanathan.
Any corrections and advice are welcome. ^ - ^

Topics Covered:

• Quadratic Residue and Quadratic Residuosity Assumption
• Goldwasser-Micali Encryption and Homomorphism
• Diffie-Hellman Key Exchange
• El Gamal Encryption

In last blog is showed one of the constructions of public-key encryption using Trapdoor Permutations, RSA encryption.

The gist in this blog is the remaining three constructions of public-key encryption.

Constructions of Public-Key Encryption:

1. Trapdoor Permutations (RSA)
2. Quadratic Residuosity/Goldwasser-Micali
3. Diffie-Hellman/El Gamal
4. Learning with Errors/Regev

Quadratic Residue

QR mod P

Let $P$ be prime.

We saw (in Lecture 6) that exactly half of $\mathbb{Z}_P^*$ are squares.

Define Legendre symbol $\left(\frac{x}{P}\right)=1$ is $x$ is square, $-1$ if $x$ is not a square, and $0$ if $x=0\mod P$.

We can tell efficiently whether $x$ is a quadratic residue mod P using Legendre symbol.

$$ \left(\frac{x}{P}\right)=x^{(P-1) / 2}=\begin{cases} 1 &,\text{ if }x \text{ is square} \\ -1 &,\text{ if }x \text{ is non-square} \\ 0 &,\text{ if }x \text{ is 0}\end{cases} $$

Then we split $\mathbb{Z}_P^*$ in half, one is square and the other is non-square.

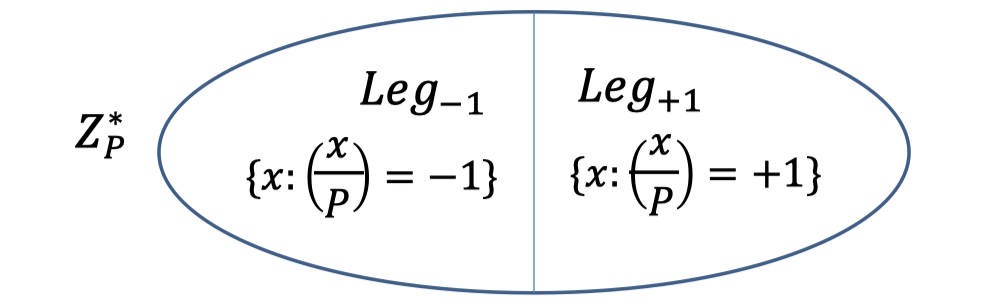
It is easy to compute square roots mod $P$.

Besides, it’s an explicit formula for the case where $P=3\pmod 4$.

Claim:

The square roots of $x \mod P$ are $\pm x^{(P+1) / 4}$.

Proof:

$\left(\pm x^{(P+1)/4}\right)^2=x^{(P+1)/2}=x\cdot x^{(P-1)/2}=x\mod P$.

QR mod N

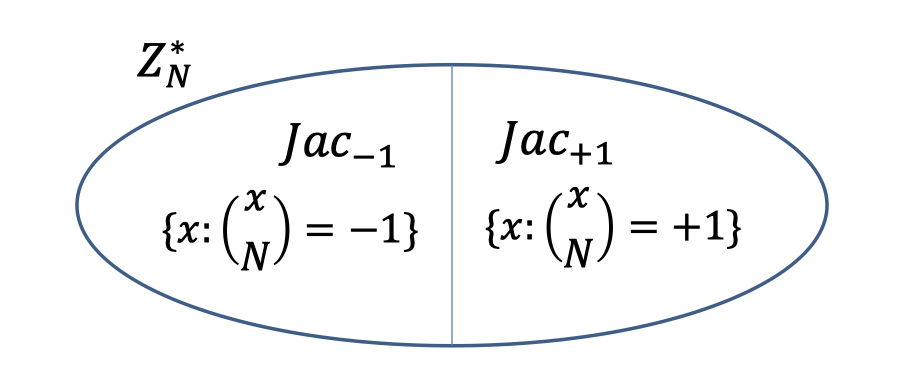
Now, let $N=PQ$ be a product of two primes and look at $\mathbb{Z}_N^*$.

Define Jacobi symbol $\left(\frac{x}{N}\right)=\left(\frac{x}{P}\right) \left(\frac{x}{Q}\right)$ to be $+1$ if $x$ is a square mod both $P$ and $Q$ or a non-square mod both $P$ and $Q$.

Jacobi Symbol — — from Wiki

The Jacobi symbol is a generalization of the Legendre symbol.
For any integer $a$ and any positive odd integer $n$, the Jacobi symbol $(\frac{a}{n})$ is defined as the product of the Legendre symbols corresponding to the prime factors of $n$:

$$ \left(\frac{a}{n}\right)=\left(\frac{a}{p_1}\right)^{\alpha_1} \left(\frac{a}{p_2}\right)^{\alpha_2}\dots \left(\frac{a}{p_k}\right)^{\alpha_k} $$

where $n=p_1^{\alpha_1}p_2^{\alpha_2}\dots p_k^{\alpha_k}$ is the prime factorization of $n$.
Some properties:

• Fix the bottom argument: $\left(\frac{ab}{n}\right)=\left(\frac{a}{n}\right)\left(\frac{b}{n}\right)$

• Fix the the top argument: $\left(\frac{a}{mn}\right)=\left(\frac{a}{m}\right)\left(\frac{a}{n}\right)$

So we can also split $\mathbb{Z}_N^*$ in half, and the Jacobi symbol for one half is $+1$ and the other is $-1$.

A surprising fact is Jacobi symbol $\left(\frac{x}{N}\right)=\left(\frac{x}{P}\right) \left(\frac{x}{Q}\right)$ is computable in poly. time without knowing $P$ and $Q$.

The key is Law of Quadratic Reciprocity.

Law of Quadratic Reciprocity:

For all $x, N$:

• $\left(\frac{x}{N}\right)=\left(\frac{N}{x}\right) \cdot (-1)^{(N-1)\cdot (x-1)/4}$

• $\left(\frac{x}{N}\right)=\left(\frac{x\mod N}{N}\right)$

• $\left(\frac{2}{N}\right)=\left(-1\right)^{\frac{\left(n-1\right)^2}{8}}$

• $\left(\frac{-1}{N}\right)=(-1)^{\frac{(n-1)}{2}}$

The one thing to notice is that the Legendre symbol$\left(\frac{x}{P}\right)$ tells you exactly whether $x$ is the square mod $P$ or not.

But the Jacobi symbol $\left(\frac{x}{N}\right)=1$ only gives you partial information that is square mod both $P$ and $Q$ or non-square mod both $P$ and $Q$.

But $x$ is square mod $N$ iff $x$ is square mod $P$ and it is a square mod $Q$.

Claim:

$x$ is square mod $N$ iff $x$ is square mod $P$ and it is a square mod $Q$.

Hence, there are two cases for $Jac_{+1}$.

• $QR_N$: the set of squares mod $N$.
• $QNR_N$: the set of non-squares mod $N$. (but with Jacobi symbol $+1$)

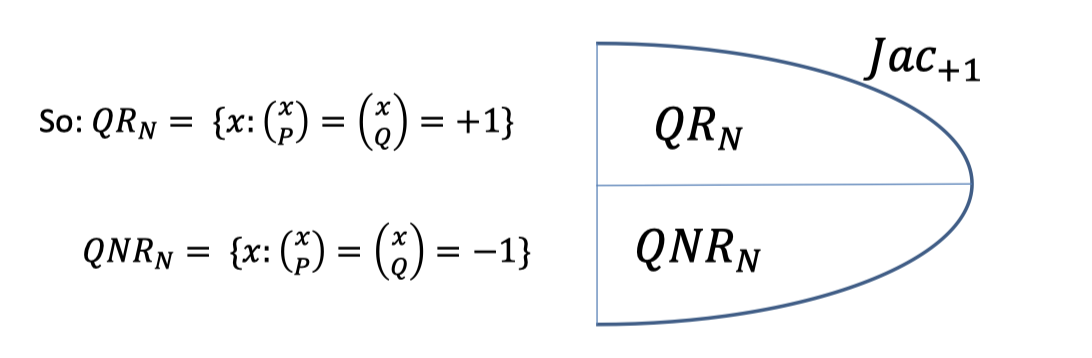
The Jacobi symbol can be $+1$ even though $x$ is not square mod $N$, so it’s pseudo-square.

The conjecture is that distinguishing between $QR_N$ and $QNR_N$ is a hard problem.

We cannot distinguish from squares and pseudo-squares.

Can we use this hardness?

Finding Square Roots Mod N

The fact is finding square roots mod $N$ is as hard as factoring $N$.

Suppose we know P and Q.

Suppose we know $P$ and $Q$, and we want to find the square root of $x \mod N$.

Before that, let’s introduce the Chinese Reminder Theorem(CRT).

It’s a nice morphism.
Informally, we can get $\mathbb{Z}_N^*\cong \mathbb{Z}_P^* \cdot \mathbb{Z}_Q^*$.

• In forward direction, we can map $\mathbb{Z}_N^*$ to $(\mathbb{Z}_P^* ,\mathbb{Z}_Q^*)$ uniquely.
  • That is: $x \rightarrow(x\mod P, x\mod Q)$.
• In back direction, we can map $(\mathbb{Z}_P^* ,\mathbb{Z}_Q^*)$ to $\mathbb{Z}_N^*$ uniquely.
  • That is: $(x_1, x_2)\rightarrow c_Px_1+c_Qx_2\mod N$.
    where $c_P$ and $c_Q$ are CRT coefficients.

We can find the square root of $x\mod N$ by following algorithm.

Algorithm:

1. Find the square roots of $y\mod P$ and $y\mod Q$.
   1. $x=y_P^2\mod P$
   2. $x=y_Q^2\mod Q$
2. Let $y=c_Py_P+c_Qy_Q$ where the CRT coefficients.
   1. $c_P=1\mod P \text{ and }0 \mod Q$
   2. $c_Q=0\mod P \text{ and }1 \mod Q$
3. Then $y$ is a square root of $x\mod N$.

Proof:

The proof is easy using CRT.

• $y^2 = (c_Py_P + c_Qy_Q)^2\mod N$
• We can map $y^2$ to pair $(y^2\mod P, y^2\mod Q)$
• Then we get pair $(y_P^2\mod P,y_Q^2 \mod Q)$
• That is $x$.
• Moreover, we can get $x=y^2\mod N \longleftrightarrow \begin{array}{c}x=y^2\mod P \\x=y^2 \mod Q\end{array}$.

Therefore, the takeaway is if $x$ is a square, it has $4$ distinct square roots $\mod N$.

Because it respectively has $2$ distinct square roots $\mod P$ and $\mod Q$.

Suppose we know square root.

Suppose we have a box that computes square roots $\mod N$.

The thing to notice is that the box only returns one square $y$ as it has $4$ distinct square roots.

So if we feed the box $x=z^2\mod N$ for a random $z$ of our choice, the box can return other square root.

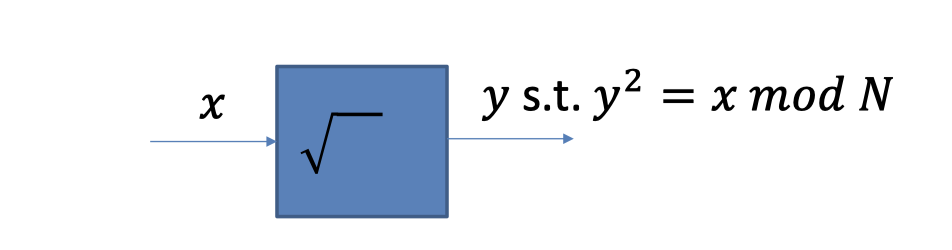
We can use the box to factor $N$.

Feed the box $x=z^2 \mod N$ for a random $z$.

Claim:

With probability $1/2$, $\operatorname{gcd}(z+y,N)$ is a non-trivial factor of $N$.

Proof:

• Notation:
  • $z$ denotes the square root of $x$, which is known.
  • $x$ denotes the input of box s.t. $x=z^2 \mod N$.
  • $y$ denotes the output of box s.t. $x=y^2\mod N$, which could be different with $z$ .
• We know $y^2=z^2\mod N$.
  • $N\mid y^2-z^2$
  • $N\mid (y-z)(y+z)$
• There are three cases.
  • If $N\mid (y-z)$, we can get $y=z\mod N$. (Useless)
  • If $N\mid (y+z)$, we can get $y=-z\mod N$. (Useless)
  • If $N\nmid (y-z)$ and $N\nmid (y+z)$, what can we get ?
    • $(y-z)$ and $(y+z)$ respectively have a factor of $N$ since $N=PQ$.
    • So $\operatorname{gcd}(z+y,N)$ is a non-trivial factor of $N$.
• Hence, $\operatorname{gcd}(z+y,N)$ is a non-trivial factor of $N$ if $y\ne z$ and $y\ne-z$.
  The probability is $1/2$.
• QED.

It’s a very clever trick to factor.

I know a solution to a problem that turns it into an Oracle.

The Oracle could actually help me in solving another problem.

It’s an example of the reduction.

Quadratic Residuosity Assumption(QRA)

Finding square roots is as hard as factoring $N$.

Moreover, recognizing squares $\mod N$ also seems hard as we mentioned above.

Quadratic Residuosity Assumption (QRA):

Let $N=PQ$ be a product of two large primes.

No PPT algorithm can distinguish between a random element of $QR_N$ from a random element of $QNR_N$ given only $N$.

Goldwasser-Micali (GM) Encryption

Goldwasser-Micali (GM) Encryption is under the Quadratic Residuosity Assumption.

GM Scheme

• $Gen(1^n)$:

  • Generate random $n$-bit prime $p$ and $q$ and let $N=pq$.

    Let $y\in QNR_N$ be some quadratic non-residue with Jacobi symbol $+1$.

    How to sample a quadratic non-residue with Jacobi symbol $+1$ ?

    1. Sample a random number $y$.

    2. Check $\left(\frac{y}{P}\right)\overset?{=} -1$ and $\left(\frac{y}{Q}\right)\overset?{=} -1$

    3. Then we can get a quadratic non-residue with $\left(\frac{y}{N}\right)=1$.

  • Let $pk=(N,y)$.

  • Let $sk=(p,q)$.

• $Enc(pk,b)$ where $b$ is a bit:

  • Generate random $r\in\mathbb{Z}_N^*$.(randomness)
  • Output $\begin{cases}r^2\mod N &, \text{if }b =0 \\r^2y\mod N &,\text{if }b=1 \end{cases}$.

• $Dec(sk,c)$:

  • Check if $c\in\mathbb{Z}_N^*$ is a quadratic residue using $p$ and $q$.
  • If yes, output $0$ else $1$.

If $b=0$, the encryption is $r^2$, which is quadratic residue with Jacobi symbol $+1$.

$\left(\frac{r^2}{N}\right)=\left(\frac{r}{N}\right)^2=1$. ( $r\in \mathbb{Z}_N^*$ so $r\ne0$)

If $b=1$, the encryption is $r^2y$, which is quadratic non-residue with Jacobi symbol $+1$.

$\left(\frac{r^2y}{N}\right)=\left(\frac{r^2}{N}\right)\left(\frac{y}{N}\right)=1$.

Although you know the Jacobi symbol is $+1$, you have no idea that the ciphertext is square or pseudo square.

Hence, IND-security follows directly from the quadratic residuosity assumption.

GM is a Homomorphic Encryption

Given a GM-ciphertext of $b$ and a GM-ciphertext of $b’$, I can compute a GM-ciphertext of $b+b’\mod 2$ without knowing anything about $b$ or $b’$.

$Enc(pk,b)$ where $b$ is a bit:
Generate random $r\in\mathbb{Z}_N^*$ and output $r^2y^b\mod N$.

Claim:

$Enc(pk,b)\cdot Enc(pk,b’)$ is an encryption of $b\oplus b’=b+b’\mod2$.

Proof:

• Consider $c_1=r_1^2y^b$ and $c_2=r_2^2y^{b’}$.
• $c_1\cdot c_2 = r_1^2r_2^2 y^{b+b’}$ .
• $c_1\cdot c_2$ is QR if $b+b’=0\mod 2$.

The takeaway here is $QR\cdot QR=QR$ and $QNR\cdot QNR=QR$.

Diffie-Hellman Key Exchange

The main idea is the commutativity in the exponent, $(g^x)^y=(g^y)^x$, where $g$ is an element of some group.

So you can compute $g^{xy}$ given either $g^x$ and $y$, or $g^y$ and $x$.

We elaborated the Diffie-Hellman Assumption in Lecture 6.

Diffie-Hellman Assumption(DHA):

Hard to compute $g^{xy}$ given only $g,g^x$and $g^y$.

---

Diffie-Hellman Key Exchange:

1. Let $p=2q+1$ be a safe prime, and $g$ be the generator of $QR_p$.
2. Alice picks a random number $x\in \mathbb{Z}_q$ and sends $g^x\mod p$ to Bob.
3. Bob picks a random number $y\in\mathbb{Z}_q$ and sends $g^y\mod p$ to Alice.

• Alice and Bob have the shared key $k=g^{xy}\mod p$
  • Alice computes it by $g^y$ and $x$.
  • Bob computes it by $g^x$ and $y$.

El Gamal Encryption

• $Gen(1^n)$:
  • Generate an $n$-bit safe prime $p=2q+1$ and a generator $g$ of $\mathbb{Z}_p^*$.
    Let $h=g^2\mod p$ be a generator of $QR_p$.
    Choose a random number $x\in \mathbb{Z}_q$.
  • Let $pk=(p,h,h^x)$.
  • Let $sk=x$.
    (Finding $sk$ from $pk$ is the discrete logarithm problem.)
• $Enc(pk,m)$ where $m\in QR_p$.
  • Generate random $y\in\mathbb{Z}_q$. (randomness)
  • Output $(h^y,h^{xy}\cdot m)$.
• $Dec(sk=x,c)$
  • Compute $h^{xy}$ using $h^y$ and $x$.
  • Divide the second component to retrieve $m$.

Decisional Diffie-Hellman Assumption (DDHA):
Hard to distinguish between $g^{xy}$ and a uniformly random group element, given $g,g^x$ and $g^y$.
That is the following two distributions are computationally indistinguishable:
$(g,g^x,g^y,g^{xy})\approx (g,g^x,g^y,u)$

From DDH assumption, we know

• It’s hard to distinguish between $(h,h^x,h^y,h^{xy})$ and $(h,h^x,h^y,u)$.
• Moreover, it’s hard to distinguish between $(h,h^x,h^y,h^{xy})$ and $(h,h^x,h^y,h^{xy}\cdot m)$ since $m$ is random, so is $m\cdot h^{xy}$.
• So it’s hard to distinguish between $(h,h^x,h^y,h^{xy}\cdot m)$ and $(h,h^x,h^y,u)$.

Hence, DH/El Gamal is IND-secure under the DDH assumption.

The source of hardness is different in RSA and GM. There is no factoring and only DH problem.

Which Group to Use

Quadratic Residue Group:

We used the $QR_P$ group for a safe prime $P=2Q+1$ where $Q$ is prime so far. The order of the group is $Q$.

But it is not used in practice.

Because discrete log can be broken in sub-exponential time $2^{\sqrt{\log P\log\log P}}$.

It’s better than $poly(P)$ but worse than $poly(\log P)$.

And the $poly(\log P)$ is what we’re referring to $poly(n)$.

---

Elliptic Curve Groups:

In practice, we use Elliptic Curve Groups in DH/El Gamal.

It is the set of solutions $(x,y)$ to the equation $y^2=x^3+ax+b\pmod P$ together with a very cool group addition law.

The best known discrete log algorithm is $\mathcal{O}(\sqrt{P})$ time!

That says that we can use much smaller keys. We can use 160-bit $P$ to suffice “80-bit security”.

Summary

We have elaborated three constructions of public-key encryption.

Constructions of Public-Key Encryption:

1. Trapdoor Permutations (RSA)
2. Quadratic Residuosity/Goldwasser-Micali
3. Diffie-Hellman/El Gamal
4. Learning with Errors/Regev

If factoring is easy, RSA is broken (and that’s the only known way to break RSA).

If factoring is easy, Goldwasser-Micali is broken conjecturing that finding square roots or recognizing the squares are both as hard as factoring.

Moreover, the discrete problem is similarly broken to factoring in quantum computer.

Hence, the preceding three constructions are dead if the quantum computer comes out.

Yet learning with errors is post-quantum secure as far as we know.

We will see more when we do homomorphic encryption.

Practical Considerations

There are some practical considerations.

• How do I know the public key?

  • Public-key Infrastructure: a directory of identities together with their public keys.
  • But it needs to be “authenticated”.
    Otherwise Eve could replace Bob’s $pk$ with her own.

• Public-key encryption is orders of magnitude slower than secret-key encryption.

  1. We mostly showed how to encrypt bit-by-bit! Super-duper inefficient.

  2. Exponentiation takes $O(n^2)$ time as opposed to typically linear time for secret key encryption (AES).

  3. The $n$ itself is large for PKE (RSA: $n\ge 2048$) compared to SKE (AES: $n=128$).
     (For Elliptic Curve El-Gamal, it’s $320$ bits.

     We can solve problem 1 and minimize problems 2&3 using hybrid encryption.

• Hybrid Encryption

  • To encrypt a long message $m$ (think 1GB)
    1. Pick a random key $K$ (think 128 bits) for a secret-key encryption.
    2. Encrypt $K$ with the $PKE$: $PKE.Enc(pk,K)$.
    3. Encrypt $m$ with the $SKE$: $SKE.Enc(K,m)$.
  • To decrypt:
    1. Recover $K$ using $sk$.
    2. Then using $K$, recover $m$.