「Cryptography-MIT6875」: Lecture 10

In this series, I will learn MIT 6.875, Foundations of Cryptography, lectured by Vinod Vaikuntanathan.
Any corrections and advice are welcome. ^ - ^

Today’s topic is Digital Signatures.

Topics Covered:

• Motivation for Digital Signatures.
• Definition: EUF-CMA Security
• One-time signatures: Lamport’s Scheme.
  • how to sign a single bit, once
  • how to sign $n$ bits, once
• Collision-resistant hashing
  • how to sign polynomially many bits, once.

Digital Signatures

Digital Signatures vs. MACs

MACs

In Lecture 5, we mentioned the applications of PRF and one of them is authentication.

Message Authentication Codes(MAC) can be evaluated by PRF, the message taken as input.

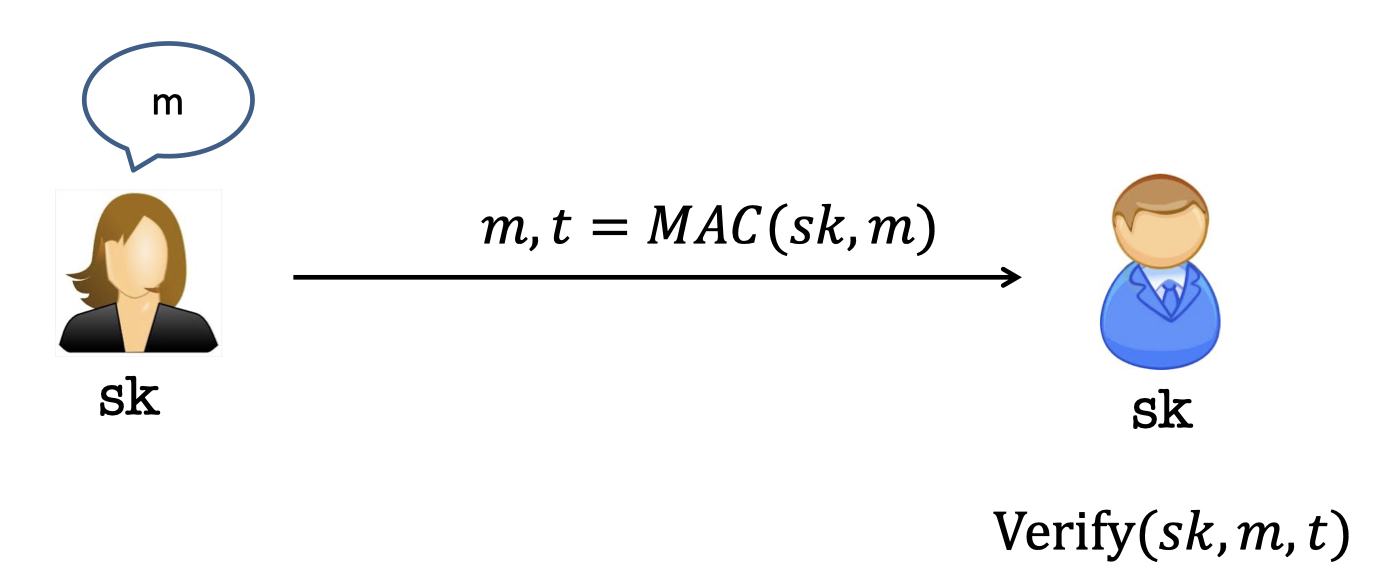
MAC gives the Authenticity that Bob is able to ensure the messages came from Alice.

Yet it needs Alice and Bob to share a secret key beforehand.

Then Alice uses the $sk$ to produce the MAC.

Digital Signatures

Digital Signatures is the Public-key analog of MACs.

The goal:

• Only Alice can produce signatures.
• Bob (or anyone else) can verify them.

There is a pair of keys, secret key $sk$ and the corresponding (public) verification key $vk$.

(Public) verification keys are stored in a “dictionary”.

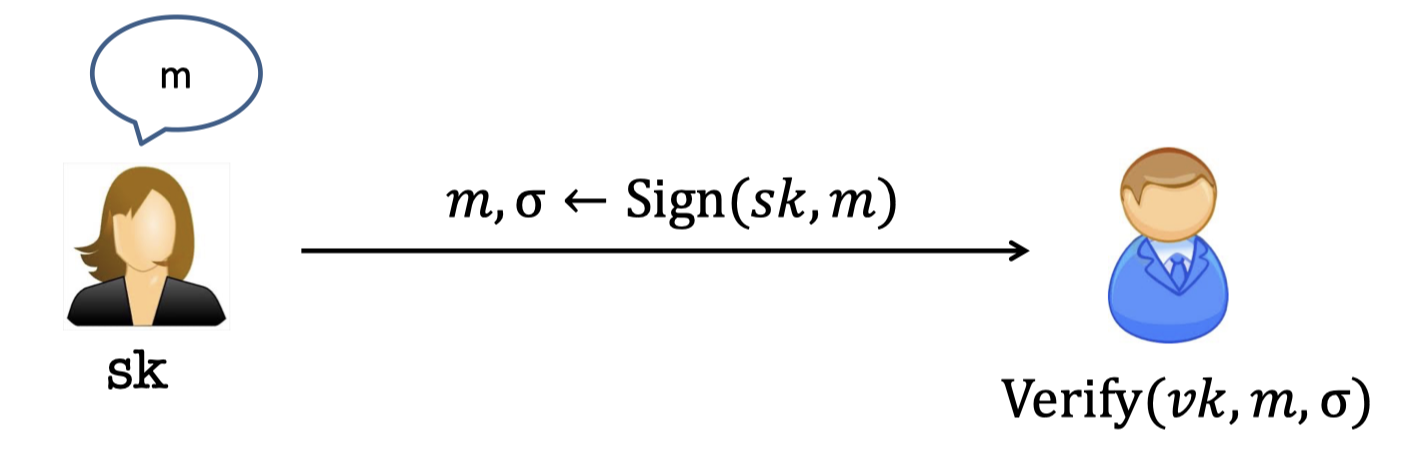
Comparison

	Signatures	MACs
1	n uses require n key-pairs	$n$ user require $n^2$ keys
2	Publicly Verifiable	Privately Verifiable
3	Transferable	Not transferable
4	Provides Non-Repudiation	Dose not provide Non-Repudiation

1. Signatures have public verification keys and private secret keys, so $n$ uses require $n$ key-pairs.
   But MAC have (private) shared keys beforehand, so $n$ users require $n^2$ keys.
2. Anyone can verify the signatures using the public $vk$.
   But only Bob who has the secret key $sk$ can verify the MACs.
3. Signatures are Transferable. That is, you can take signatures and show it to others.
4. Signatures provides Non-Repudiation. That is, you cannot claim that you didn’t sign it.[*不可抵赖]

Transferability and Non-Repudiation whether they are good properties or bad properties depends on the scenario. It is double edged sword.

Applications

There are abundant applications of signatures.

1. Certificates, or a public-key directory in practice.
   • Trusted Certificate Authority(CA), e.g. Verisign, Let’s Encrypt.
   1. When Alice (=www.google.com) wants to register her public (encryption and signing) keys $pk$ and $vk$, CA first checks that she is Alice.
   2. CA issues a “certificate” $\sigma\leftarrow Sign(SK_{Verisign},Alice||pk||vk)$.
      The certificate is essentially the signature.
      The certificate indicates that $pk$ and $sk$ are indeed Alice’s.
   CA produces the signature using its sign key $SK_{Verisign}$.
   3. Alice can later stores this certificate to prove she “owns” $pk$ and $sk$.
   4. Browsers store $VK_{Verisign}$ and check the certificate.
      $VK_{Verisign}$ is the public verification key of CA.
2. Bitcoin and other cryptocurrencies.
   • I am identified by my verification key $vk$.
   • When I pay you (your verification key = $vk’$), I sign “$x$ paid to $vk’$” with my $sk$.

Definition

The definition of Digital Signatures consists of a triple of PPT algorithms $(Gen,Sign,Verify)$.

• $Gen(1^n)\rightarrow (vk,sk)$ running by Alice(signer)
  PPT Key Generation algorithm generates a public-private key pair.
• $Sign(sk,m)\rightarrow \sigma$ running by Alice (signer)
  (possible probabilistic) Signing algorithm uses the secret signing key to produce a signature $\sigma$.
  Whether deterministic or probabilistic Signing algorithm makes sense.
• $Verify(vk,m,\sigma)\rightarrow Acc(1)/Rej(0)$ running by Bob (any verifier)
  Verification algorithm uses the public verification key to check the signature $\sigma$ against a message $m$.

Correctness:

For all $vk,sk,m$: $Verify(vk,m,Sign(sk,m))=accept$.

EUF-CMA Security

Define the adversary first.

The adversary after seeing signatures of many messages, should not be able to produce a signature of any new message.

Adversary:

• Power of adversary: Chosen-message attack
  The adversary can request for, and obtain, signatures of (poly. many) messages $m_1,m_2,\dots$
• Goal of adversary: Existential Forgery
  The adversary wins if she produces a signature of any new message $m^*\notin \{m_1,m_2,\dots \}$.

Then we give Existentially Unforgeable against a Chosen Message Attack (EUF-CMA) security by a game.

Game :

1. The Challenger generates a public-private key pair $(vk,sk)$ and sends the public verification key $vk$ to Eve.
2. Eve can request for poly. many messages $\{m_1,m_2,\dots\}$ and obtain the corresponding signatures $\{\sigma_1,\sigma_2,\dots\}$.
3. Eve produce a signature $\sigma^*$ against a new message $m^*\notin \{m_1,m_2,\dots\}$.

EUF-CMA Definition:

Eve wins if $Verify(vk,m^*,\sigma^*)=1$ and $m^*\notin\{m_1,m_2,\dots\}$.

The signature scheme is EUF-CMA-secure if no PPT Eve can win with probability better than $negl(n)$.

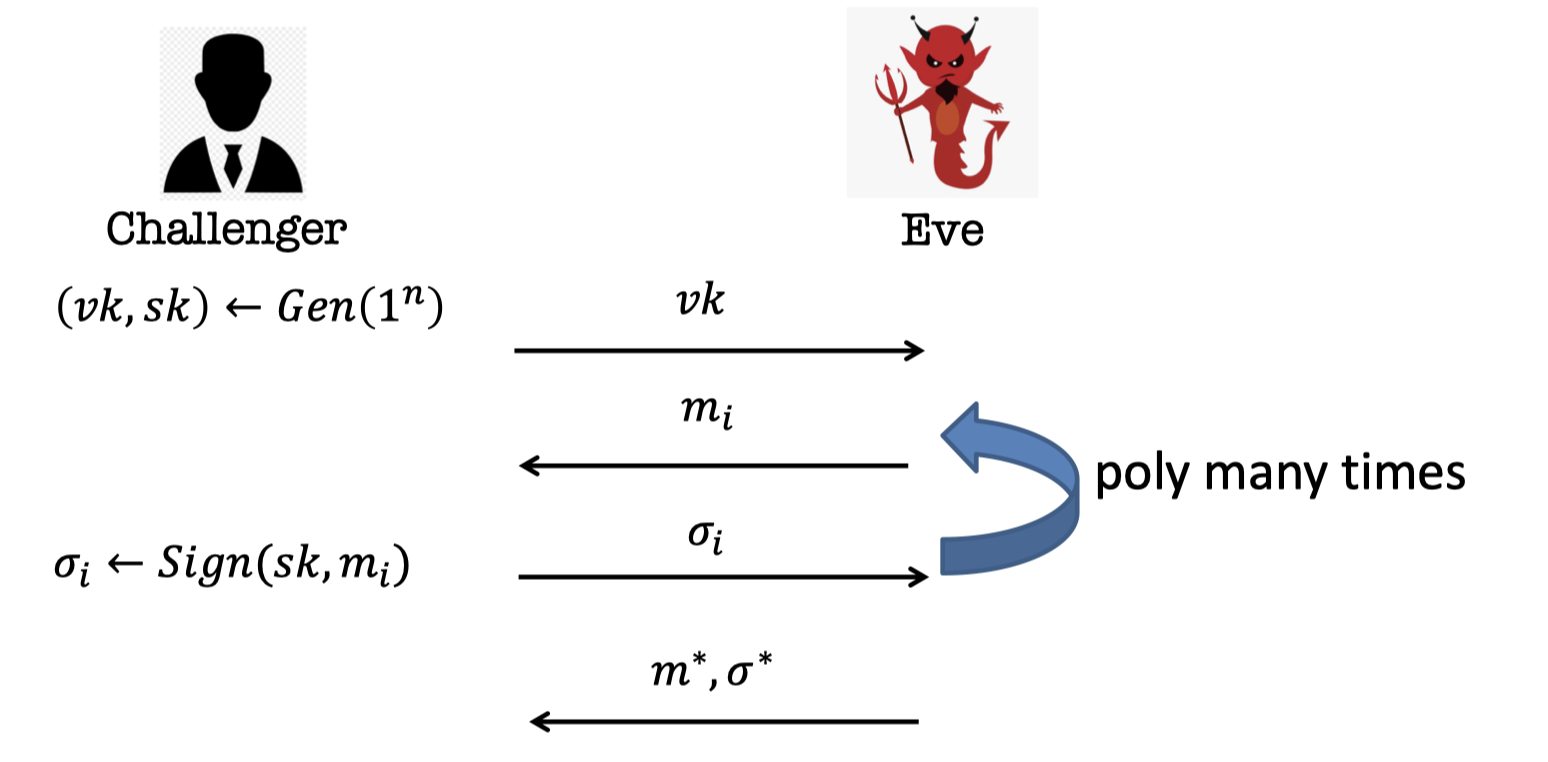
The challenger gives Eve a lot of signatures.

Now Eve wants to forge a signature of other message right.

We say that she wins if she produces a signature right of even one message that was not signed already.

We call this an existential forgery because there exists a $m^*$ not in the set for which she produces a signature.

It’s a very strong definition.

But the definition dose not prevent the adversary from producing a new signature for the same message.

Yet she dose not win.

In other words, it’s consistent with the definition to allow the adversary to produce a new signature for the same message.

We can make the job easier for adversary. She wins as well if she produces a new signature for the same message.

Then we can get strong EUF-CMA definition.

So the stronger adversary, the stronger security by definition.

Lamport (One-time) Signatures

In this section, we introduce a beautiful signature, Lamport Signature.

It’s One-time signature sort of like One-time Pads.

The one-time signatures means that the adversary gets a signature of some message once, a single message, and she should not be able to produce a signature of any other different message.

How to sign a bit

We only use the signing key to sign once and we are really signing a bit.

• $Gen(1^n)\rightarrow (SK,VK)$
  • Signing Key $SK:[x_0,x_1]$
    where $x_0,x_1$ are both $n$-bit string.
  • Verification Key $VK:[y_0=f(x_0),y_1=f(x_1)]$
    where $f$ is a OWF.
• $Sign(SK,b)\rightarrow \sigma$ where $b$ is a bit
  • The signature is $\sigma=x_b$.
• $Verify(VK,b,\sigma)$
  • Check if $f(\sigma)\overset ? = y_b$

The signing keys $SK$ are two random $n$-bit string and the verification keys $VK$ are the corresponding values of OWF, i.e. the signing keys are images of verification keys.

The game in Lamport (One-time) Signatures differs from that Eve only gets a signature of a single message.

If $b=0$, the challenger gives Eve $x_0$, the signature of $0$, and Eve wants to forge the signature of $1$.

So the task of adversary is producing a signature of $1$.

That’s $x_1$. She cannot do it because $x_1$ is random.

Claim :

Assuming $f$ is a OWF, no PPT adversary can produce a signature of $\bar{b}$ given a signature of $b$.

The intuition of proof is easy.

There’s no way Eve can produce $x_1$ unless she can invert the $y_1$ she have.

How to sign n bits

We can use the signing keys to sign $n$ bits, once.

Just repeat it.

• $Gen(1^n)\rightarrow (SK,VK)$
  • Signing Key $ SK:\left[\begin{array}{c}x_{1,0},x_{2,0},\dots, x_{n,0}\\ x_{1,1},x_{2,1} ,\dots, x_{n,1}\end{array} \right]$
    where $x_{\cdot,\cdot}$ is $n$-bit random string and each column is a pair-key for one bit.
  • Verification Key $VK:\left[\begin{array}{c}y_{1,0},y_{2,0},\dots, y_{n,0}\\ y_{1,1},y_{2,1} ,\dots, y_{n,1}\end{array} \right]$
    where $f$ is a OWF and $y_{i,c}=f(x_{i,c})$.
• $Sign(SK,\vec m)\rightarrow \vec\sigma$ where $m$ is a $n$-bit message $(m_1,\dots, m_n)$.
  • The signature is $\vec \sigma=(x_{1,m_1},\dots, x_{n,m_n})$.
• $Verify(VK,\vec m,\vec\sigma)$
  • Check if $\forall i:f(\sigma_i)\overset ? = y_{i,m_i}$.

In the game, Eve can request for a signature once of any $n$-bit message $m$ and she wants to forge the signature of a different message $m’\ne m$.

There are two claims.

Claim 1:

Assuming $f$ is a OWF, no PPT adversary can produce a signature of $m’$ given a signature of a single message $m\ne m’$.

Claim 2:

The adversary can forge signature on any message given the signatures on (some) two messages.

We only give the proof of Claim 1.

Claim 2 can be comprehended easily after proving Claim1.

Proof for Claim 1:

Suppose for the contradiction that there is a adversary forging a signature of $m’$ given a signature of a single message $m$ s.t. $m’\ne m$.

We want to construct a OWF Inverter for $y$ so we need to interact with the forger.

Interaction with the forger:

1. Inverter gives the verification keys $VK$ to the forgery.
2. The forger request for a signature of a single message $m$.
3. Inverter produces the signature $\sigma$ she wants.
4. Then the forger promises to give a signature $\sigma’$ against a new message $m’$

The key idea is we can take $y$ into $VK$ and plop it into one of the two slots in one column.

The thing to notice is that there is at least one different bit between $m$ and $m’$.

Note:

• The message $m$ is what the forger wants to obtain its signature
• The message $m’$ is what the forger wants to forge its signature.

For simplicity, we suppose there is only one different bit between $m$ and $m’$.

messages $m$ and $m’$ are known in advance:

• Suppose the Inverter knows $m$ and $m’$in advance.
  For simplicity, suppose $m=00\dots 0$ and $m’=10\dots 0$.

• The Inverter wants to get the inverse of $y$ against the OWF $f$.

• So the Inverter interacts with the forger.

  1. The Inverter samples $SK$ and generates the verification keys (put $y$ into one slot as follows)

     $$ VK=\left[\begin{array}{c}f(x_{1,0}) &,f(x_{2,0}),\dots, f(x_{n,0})\\ y &,f(x_{2,1}) ,\dots, f(x_{n,1})\end{array} \right] $$

     where $x_{\cdot,\cdot}$ is known to the Inverter.

  2. The forger requests for the signature of $m=00\dots 0$.

  3. The Inverter produces the signature $\sigma=(x_{1,0},\dots,x_{n,0})$.

  4. The forger promises to produce the signature on $m’=10\dots0$ from the contradiction which has the inverse of $y$.

• Done.

However, the Inverter dosen’t know the two messages in advance.
The Invert only knows there is one different bit between $m$ and $m’$.

So the Inverter could guess it.

messages $m$ and $m’$ are unknown in advance:

• The Inverter guesses the different bit locates in $i$-th bit right w.p. $1/n$.

• Suppose the Inverter plants the trap $y$ into the slot $(i,0)$, $i$-th column and $0$-th row.
  Then the generated verification keys is as follows.

  $$ VK=\left[\begin{array}{c}f(x_{1,0}) ,\dots ,&y&,\dots, f(x_{n,0})\\ f(x_{1,1}) ,\dots ,&f(x_{i,1})& ,\dots, f(x_{n,1})\end{array} \right] $$

  where $x_{\cdot,\cdot}$ is known to the Inverter.

• In the forger’s point of view, when she looks at the verification keys $VK$, she has no information about where the trap is.

• There are two events that could happen even if $m$ differs from $m’$ in $i$-th bit.

  • The message $m$ hits the trap while the $m’$ dose not hit the trap.
  • The message $m$ dosen’t hit the trap while the $m’$ hits the trap.

• The Inverter can only handle with the second event.
  The message $m$ hits the opposite location to the trap while the $m’$ hits the trap.

  • The Inverter is able to give the signature of $m$, i.e. $(\dots,x_{i,1},\dots)$
  • The forger promises to produce the signature of $m’$from the contradiction, which have the inverse of $y$.
  • Otherwise, the forger gives something that the Inverter already has known.

• So the probability of inverting right is $\varepsilon/2n$ if the advantage of forging is non-negligibly $\varepsilon$.
  The $1/n$ is the probability of guessing the location of different bit and the $1/2$ is the probability of guessing whether $m$ hits the trap.

• Done.

Besides, Claim 2 says that once I give you the two signatures, I am actually giving you all the inverses and you can produce signatures of any message you want.

This violates one-wayness.

So far, the length of message is limited by the size of verification keys.

Before proceeding to the next question that how to sign poly. many bits, we take a detour in collision-resistant hash function.

Detour: Collision-Resistant Hash Functions

A compressing function $h:\{0,1\}^m\rightarrow \{0,1\}^n$ (where $m>n$ ) for which it is computationally hard to find collisions.

It compresses the bits sort of the opposite of PRG.

Definition:

$h$ is collision-resistant if for every PPT algorithm $A$, there is a negligible function $\mu$ s.t.

$$ \operatorname{Pr}[A(1^n)=(x,y):x\ne y, h(x,y)]=\mu(n) $$

In theory, we like to talk about families of functions to handle non-uniform adversaries (who could have hardcoded collision for the fixed function $h$).

A compressing family of functions $\mathcal{H}=\{\{0,1\}^m\rightarrow \{0,1\}^n\}$ (where $m>n$) for which it is computationally hard to find collisions.

Collision-Resistant Definition:

$\mathcal{H}$ is collision-resistant if for every PPT algorithm $A$, there is a negligible function $\mu$ s.t.

$$ \operatorname{Pr}_{h\gets \mathcal{H}}[A(1^n)=(x,y):x\ne y, h(x,y)]=\mu(n) $$

How to sign poly. many bits

Back to the question that how to sign poly. many bits with a fixed verification key.

The key idea is hashing the message into $n$ bits and sign the hash.

• $Gen(1^n)\rightarrow (SK,VK)$
  • Signing Key $SK:\left[\begin{array}{c}x_{1,0},x_{2,0},\dots, x_{n,0}\\ x_{1,1},x_{2,1} ,\dots, x_{n,1}\end{array} \right]$
    where $x_{\cdot,\cdot}$ is $n$-bit random string and each column is a pair-key for one bit.
  • Verification Key $VK:\left[\begin{array}{c}y_{1,0},y_{2,0},\dots, y_{n,0}\\ y_{1,1},y_{2,1} ,\dots, y_{n,1}\end{array} \right]$
    where $f$ is a OWF and $y_{i,c}=f(x_{i,c})$.
  • Sample $h\gets \mathcal{H}$.
• $Sign(SK,\vec m)\rightarrow \vec\sigma$ where $m$ is a $n$-bit message $(m_1,\dots, m_n)$.
  • Compute the hash $z=h(m)$.
  • The signature is $\vec \sigma=(x_{1,z1},\dots, x_{n,z_n})$.
• $Verify(VK,\vec m,\vec\sigma)$
  • Recompute the hash $z=h(m)$
  • Check if $\forall i:f(\sigma_i)\overset ? = y_{i,z_i}$.

Claim :

Assuming $f$ is a OWF and $\mathcal{H}$ s a collision-resistant family, no PPT adversary can produce a signature of $m’$ given a signature of a single $m\ne m’$.

We only give the idea of proof.

Intuition of Proof:

Suppose for the contradiction.

There are two possibilities.

• Either the adversary picked $m’$ s.t. $h(m’)=h(m)$, in which case she violated collision-resistance of $\mathcal{H}$.
• Or she produced a Lamport signature on a “message” $z’\ne z$, in which case she violated one-time security of Lamport, and therefore the one-wayness of $f$.