「Cryptography-MIT6875」: Lecture 11

In this series, I will learn MIT 6.875, Foundations of Cryptography, lectured by Vinod Vaikuntanathan.
Any corrections and advice are welcome. ^ - ^

Today’s topic is Many-time Digital Signatures.

Topics Covered:

• Many-time, stateful, signature schemes.
• Naor-Yung construction: stateless EUF-CMA-secure signature schemes.

In last blog was introduced the definition of Digital Signatures and the EUF-CMA Security.

Moreover, we introduced Lamport (One-time) Digital Signatures.

We can use it to sign polynomially many bits with a fixed verification key.

The main idea is hashing the message into $n$ bits and signing the hash.

So far, it’s one-time security. The adversary can forge signature on any message given the signatures on (some) two messages.

How to achieve Many-time Signature Scheme ?

It’s today’s gist.

We will achieve many-time signature scheme in four+ steps.

1. Stateful, Growing Signatures.
   Idea: Signature Chains
2. How to Shrink the signatures.
   Idea: Signature Trees
3. How to Shrink Alice’s storage.
   Idea: Pseudorandom Trees
4. How to make Alice stateless.
   Idea: Randomization
5. (optional). How to make Alice stateless and deterministic.
   Idea: PRFs.

S1: Stateful Many-time Signatures

The first step is to achieve stateful many-time signatures.

The main idea is Signature Chains.

sign m1

• Alice starts with a secret signing Key $SK_0$.
  Her public verification Key $VK_0$ is stored in the (public) “directory”.

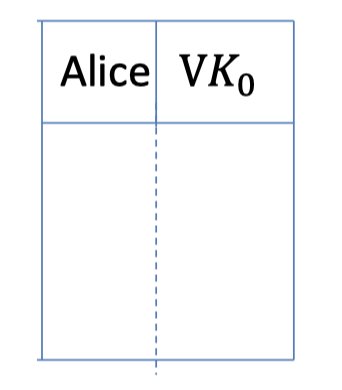
• When signing a message $m_1$:

  1. Generate a new pair $(VK_1,SK_1)$.
  2. Produce signature $\sigma_1\leftarrow Sign(SK_0,m_1||VK_1)$.
  3. Output $VK_1||\sigma_1$
  4. Remember $VK_1||m_1||\sigma_1$ as well as $SK_1$.
  • Alice is going to sign not only the message, but the message together with the next verification key.
  • She uses it to authenticate a new verification.
  • It’s the concatenation of two strings and we can sign polynomially many bits.

• To verify a signature $VK_1||\sigma_1$ for message $m_1$:

  • Run $Verify(VK_0,m_1||VK_1,\sigma_1)$.

    

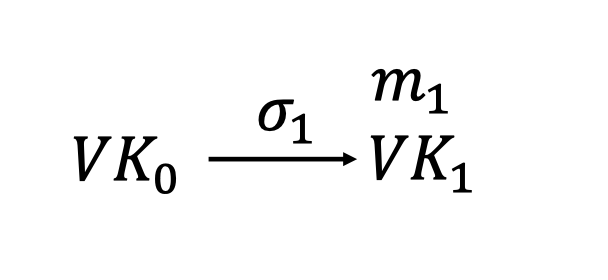
  • We use $VK_0$ to verify the signature $\sigma_1$ that $m_1$is sent from Alice and $VK_1$ is authenticated from Alice.

sign m2

But how about the next message $m_2$ ?

Can we just output $VK_2||\sigma_2$ as follows ? (NO!)

• When signing the next message $m_2$:
  1. Generate a new pair $(VK_2,SK_2)$.
  2. Produce signature $\sigma_2\leftarrow Sign(SK_1,m_2||VK_2)$.
  3. Output $VK_2||\sigma_2$

The thing to point is that each signing is independent and everyone only knows the verification key $VK_0$ in that “directory”.

The verifier dosen’t know the verification key $VK_1$ for the signature $\sigma_2$ nor the authentication for $VK_1$ when he receives $VK_2||\sigma_2$.

---

So Alice needs to send $VK_1$ as well as the authentication for $VK_1$.

We should output $VK_1||m_1||\sigma_1||VK_2||\sigma_2$ as follows.

• When signing the next message $m_2$:

  1. Generate a new pair $(VK_2,SK_2)$.
  2. Produce signature $\sigma_2\leftarrow Sign(SK_1,m_2||VK_2)$.
  3. Output $VK_1||m_1||\sigma_1||VK_2||\sigma_2$.
  4. (additionally) Remember $VK_2||m_2||\sigma_2$ as well as $SK_2$.
  • The first part $VK_1||m_1||\sigma_1$ is to authenticate the verification key $VK_1$.
  • The verify uses $VK_1$ to verify the message $m_2$ together with the next verification $VK_2$.

• To verify a signature $VK_1||m_1||\sigma_1||VK_2||\sigma_2$ for message $m_2$:

  1. Run $Verify(VK_0,m_1||VK_1,\sigma_1)$ to authenticate $VK_1$.

  2. Run $Verify(VK_1,m_2||VK_2,\sigma_2)$ to authenticate the message $m_2$ together with the next verification key $VK_2$.

     

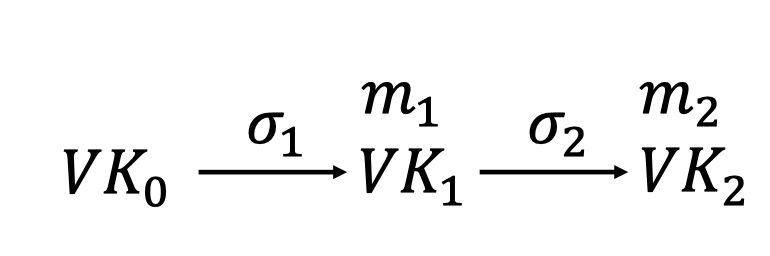
It’s growing signatures since Alice needs remember the $VK_i||m_i||\sigma_i$ as well as $SK_i$.

And the signature chains is as follows.

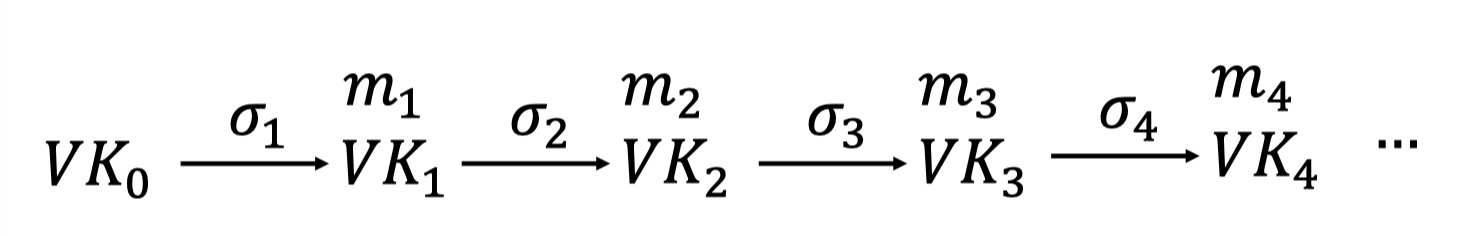
An optimization

In fact, Alice stores the $m_i$ just to use $\sigma_i$ to authenticate $VK_i$.

So there is an optimization that need to remember only the past verification keys, not the past messages.

Suppose we can split the verification into two halves.

We use part of $VK_i$ to sign $m_{i+1}$ and the rest to sign $VK_{i+1}$.

The signature chains is as follows.

The verifier only needs to verify the past verification keys, not the past messages.

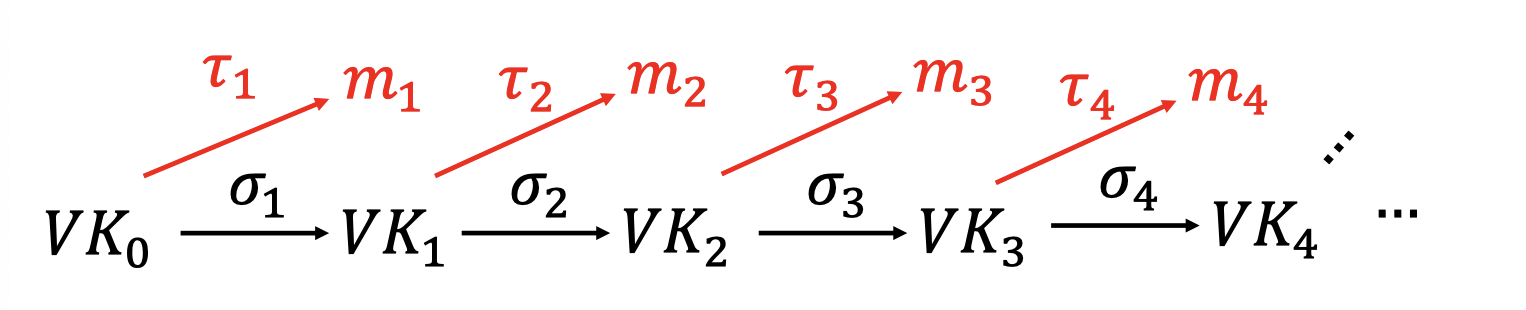
Problems

There are still two major problems.

1. Alice is stateful.
   Alice needs to remember a whole lot of things, $\mathcal{O}(T)$ information after $T$ steps.
2. The signatures grow.
   Length of the signature of the $T$-th message is $\mathcal{O}(T)$.

S2: How to Shrink the signatures ?

The next step is to shrink the signature.

The main idea is Signature Trees.

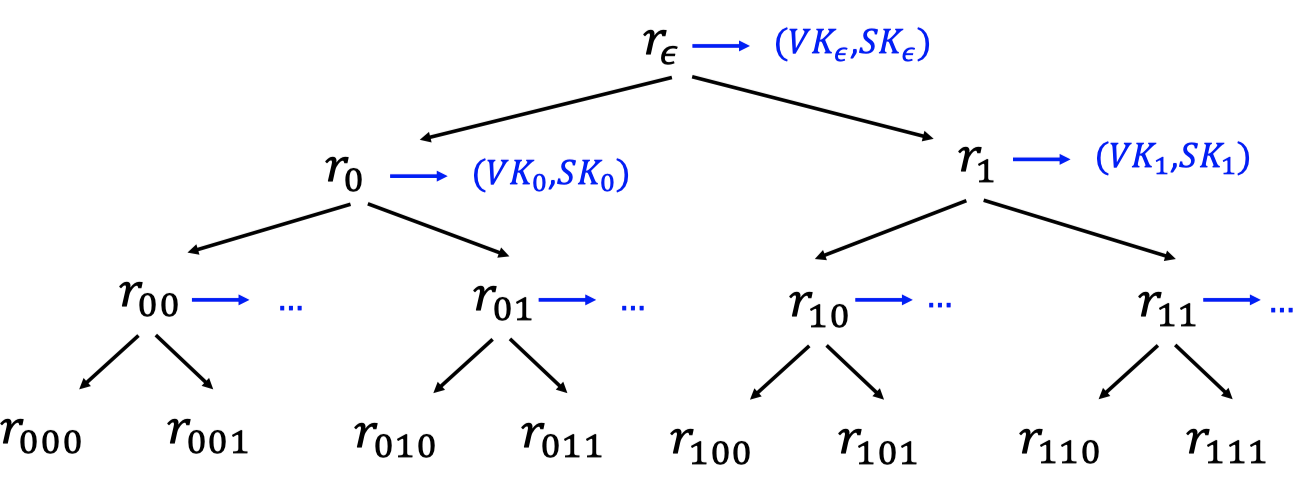
• Alice starts with a secret signing Key $SK_\epsilon$.
  Her public verification Key $VK_\epsilon$ is stored in the (public) “directory”.

• Alice generates many random $(VK,SK)$ pairs and arrange them in a tree of depth = security parameter $\lambda$.
  There are $2^\lambda$ leaves and Alice only uses the leaf to sign the message.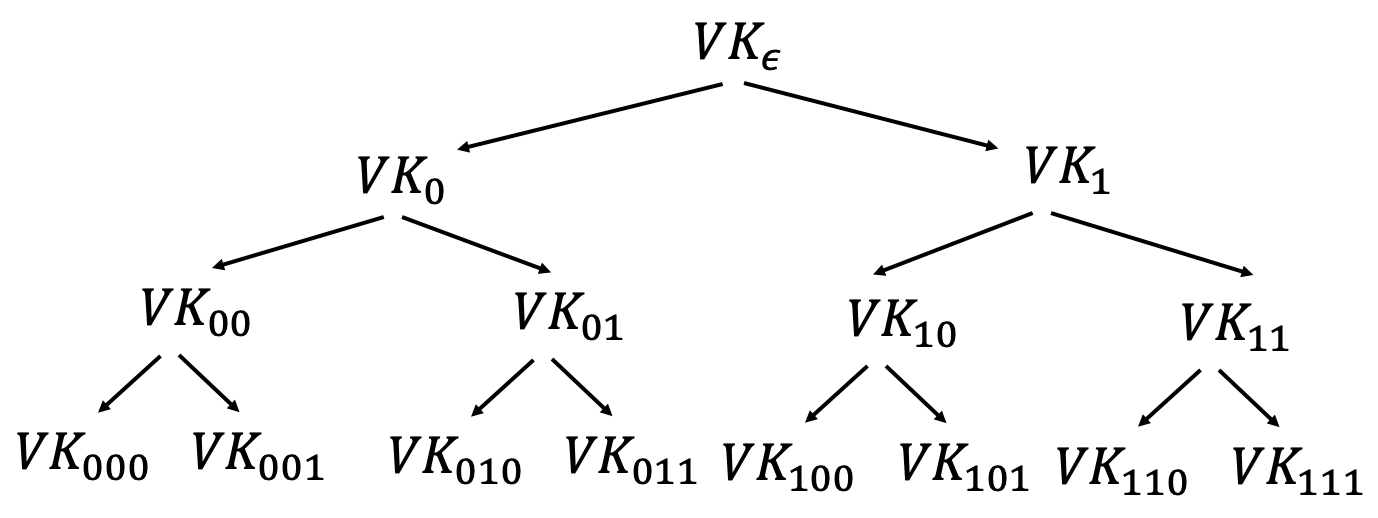

  

• When signing the first message $m_0$

  • Alice only uses the leaf to sign the message while use the parent node to sign both children nodes.

    

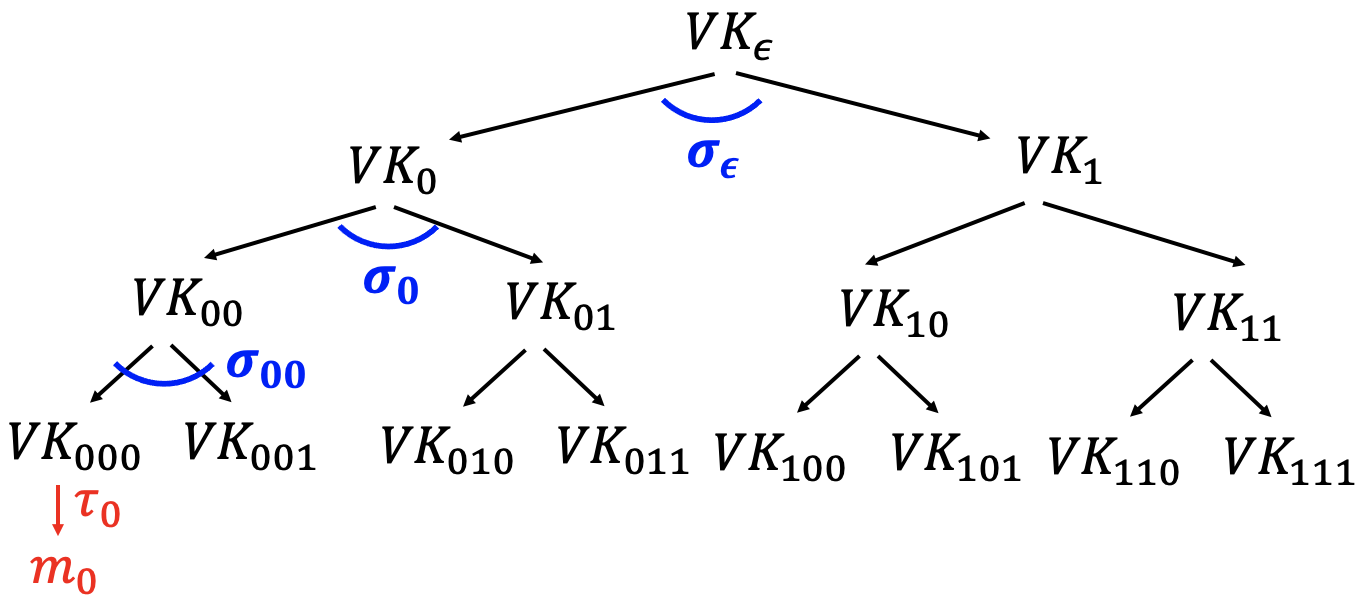
  • Use $VK_{000}$ to sign $m_0$.

    • $\tau_0\gets Sign(SK_{000},m_0)$

  • “Authenticate ” $VK_{000}$ using the “signature path”.
    Alice produces the authentication path for $VK_{000}$ : $(\sigma_\epsilon,\sigma_0,\sigma_{00})$.

    1. Authenticate $VK_0$: use $VK_\epsilon$ to sign both $VK_0$ and $VK_1$
       $\sigma_\epsilon\gets Sign(SK_\epsilon,VK_{0},VK_{1})$

       2. Authenticate $VK_{00}$: use $VK_{0}$ to sign both $VK_{00}$ and $VK_{01}$
          $\sigma_0\gets Sign(SK_0,VK_{00},VK_{01})$

       3. Authenticate $VK_{000}$: use $VK_{00}$ to sign both $VK_{000}$ and $VK_{001}$

          $\sigma_{00}\gets Sign(SK_{00},VK_{000},VK_{001})$

  • Signatures of $m_0$: (Authentication path for $VK_{000}$, $\tau_0\gets Sign(SK_{000},m_0)$)

• When signing the next message $m_1$

  
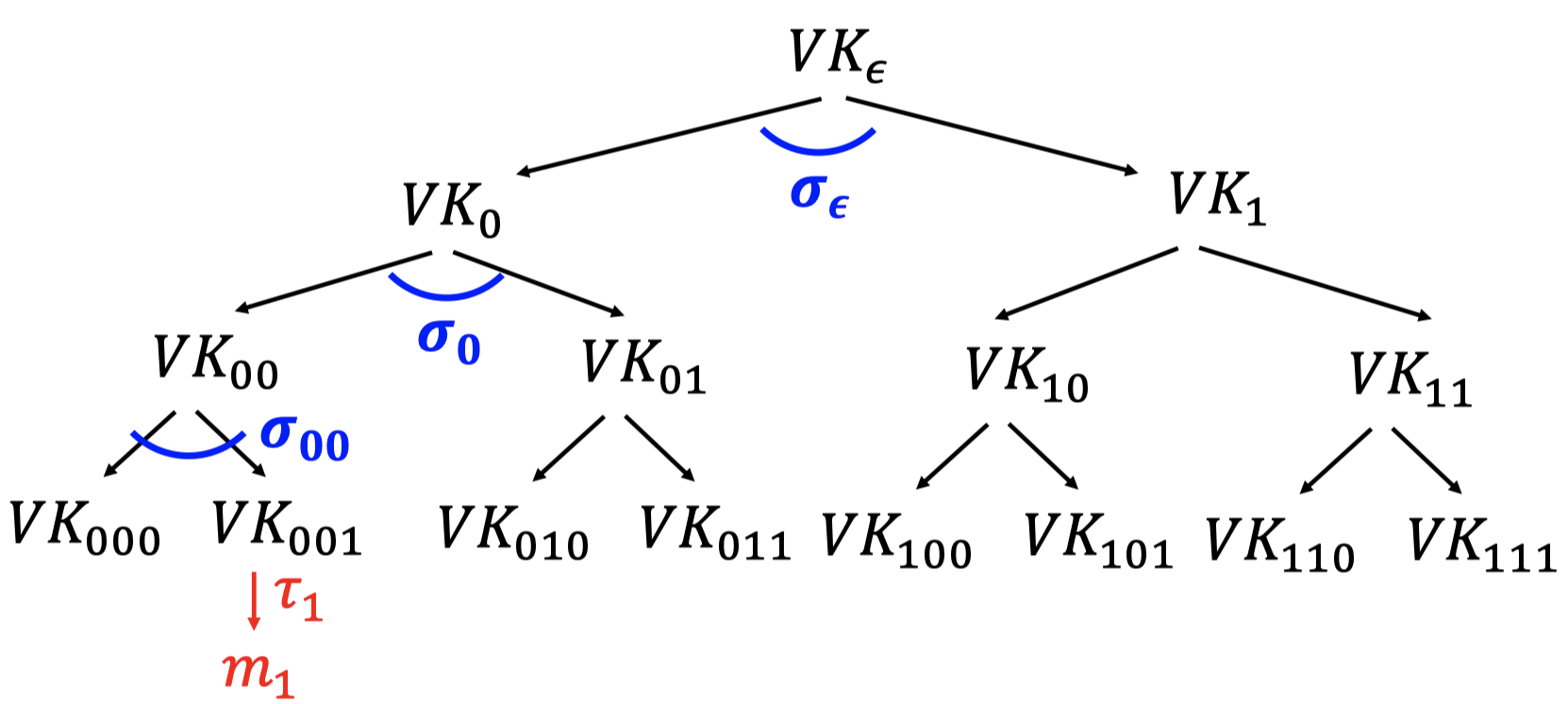
  • Use $VK_{001}$ to sign $m_1$.
    • $\tau_1\gets Sign(SK_{001},m_1) $
  • “Authenticate ” $VK_{001}$ using the “signature path”.
    Alice produces the authentication path for $VK_{001}$ : $(\sigma_\epsilon,\sigma_0,\sigma_{00})$.
    1. Authenticate $VK_0$: $\sigma_\epsilon\gets Sign(SK_\epsilon,VK_{0},VK_{1})$
    2. Authenticate $VK_{00}$: $\sigma_0\gets Sign(SK_0,VK_{00},VK_{01})$
    3. Authenticate $VK_{000}$: $\sigma_{00}\gets Sign(SK_{00},VK_{000},VK_{001})$
  • Signatures of $m_1$: (Authentication path for $VK_{001}$, $\tau_1\gets Sign(SK_{001},m_1)$)

The good news is the signatures consist of $\lambda$ one-time signatures and do not grow with time.

But the bad news is the signer generates and keeps the entire ($\approx 2^\lambda$-size) signature tree in memory.

Besides, the signer also needs to remember the state that what is the last leaf used for signing.

S3: How to Shrink Alice’s storage.

The main idea is Pseudorandom Trees.

Instead of truly random signature trees, Alice uses PRF to build a pseudorandom signature trees.

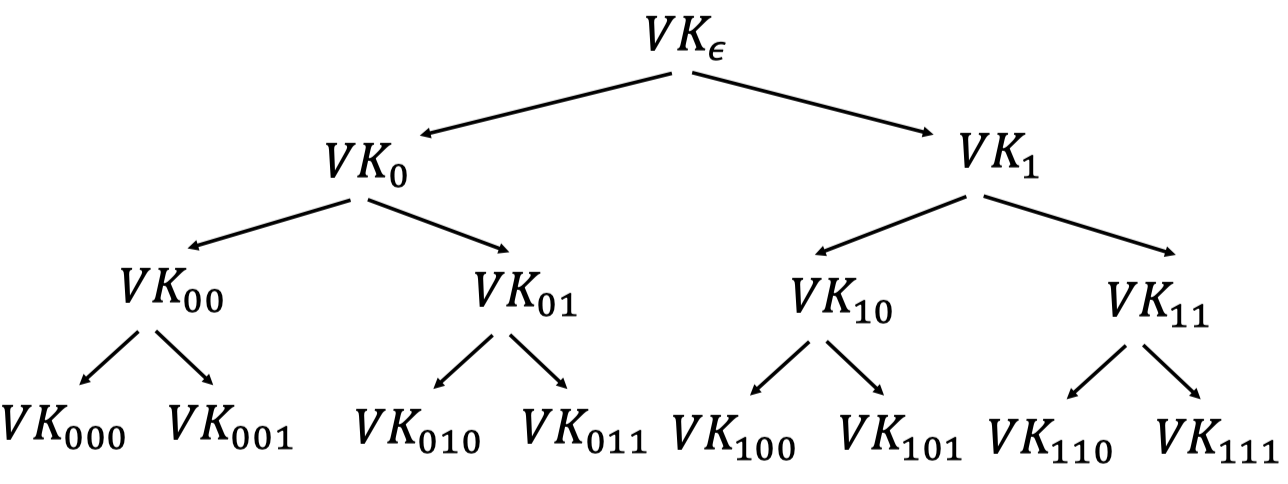
• Alice keeps a secret PRF key $K$.
• Alice populates the nodes with $r_x=PRF(K,x)$
• Use $r_x$ to derive the key pair $(VK_x,SK_x)\gets Gen(1^\lambda;r_x)$.
• The thing to notice is that Alice only registers the verification key $VK_\epsilon$.
  So the verifier only knows $VK_\epsilon$, not the PRF key.

We can use the pseudorandom signature tree to sign many-time signatures same as above.

As a matter of fact, the signer can do lazy evaluation instead of evaluating every node beforehand.

So the signer can achieve short signatures and small storage at the same time.

However, it’s still stateful.

The signer still needs to keep a counter indicating which leaf (which tells her which secret key) to use next.

It proceeds to the next step.

S4: How to make Alice stateless.

The main idea is randomization.

We can achieve stateless via randomization.

• When signing a message $m$

  
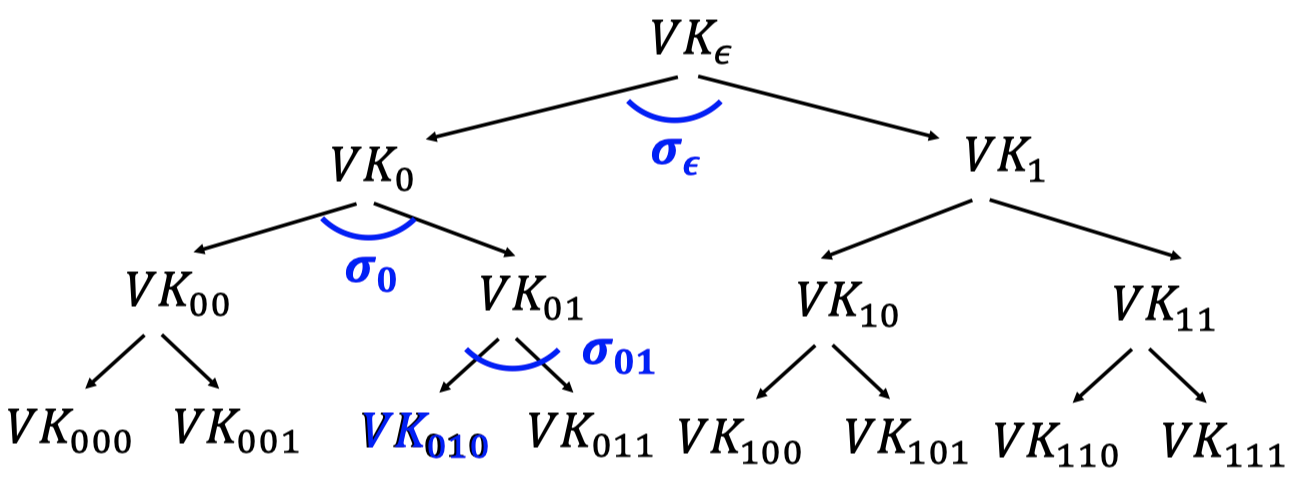
  1. Pick a random leaf $r$.
  2. Use $VK_r$ to sign $m$.
     $\sigma_r\gets Sign(SK_r,m)$
  3. Output $(r,\sigma_r,\text{authentication path for }VK_r)$.

The good news is it’s stateless.

But we cannot pick the same leaf twice since we are using the one-time signature scheme.

The key idea of security analysis is birthday attack.

If the signer produces $q$ signatures, the probability she picks the same leaf twice is $\le q^2/2^\lambda$, which is negligible.

S5: How to make Alice stateless and deterministic.

The key idea is generating $r$ pseudo-randomly.

Have another PRF key $K’$ and let $r=PRF(K’,m)$.

• When signing a message $m$

  
  1. Pick a pseudorandom leaf $r=PRF(K’,m)$.
  2. Use $VK_r$ to sign $m$.
     $\sigma_r\gets Sign(SK_r,m) $
  3. Output $(r,\sigma_r,\text{authentication path for }VK_r)$.

Security Analysis

For simplicity, we analyze the randomization stateless scheme. (S4)

The many-time digital signature scheme is EUF-CMA secure if the one-time digital signature is one-time secure.

Assume for the contradiction that there is an adversary breaking the EUF-CMA security, then we can construct a one-time forger.

• We have the adversary $\mathcal{A}$ for EUF-CMA security.
  1. Get the verification key $VK$.
  2. Request for signatures of $q$ messages. ($q$-time)
     1. Request for message $m_i$
     2. Obtain the signature $\sigma_i$ for $m_i$.
  3. Produce $(m^*,\sigma^*)$ that a signature against a new message $m^*\notin \{m_1,m_2,\dots m_q\}$ with non-negligible advantage.
• We want to construct a forger $\mathcal{B}$ for one-time security.
  1. Get the one-time verification key $OVK$.
  2. Request for the signatures $\sigma$ of a single message $m$. (only one-time)
  3. Produce $(m’,\sigma’)$ that a signature against a new message $m’\ne m$.
• For simplicity, we condition on the event $E$ where all our random $r$’s are distinct.
  • $\operatorname{Pr}[\mathcal{A}\text{ wins }\mid E]\ge q^2/2^\lambda$
  • Suppose the probability above dosen’t change very much.
  • $\ge \operatorname{Pr}[\mathcal{A}\text{ wins }]-\operatorname{Pr}[E]=1/poly(\lambda)-negl(\lambda)$
  • $\ge 1/poly(\lambda)$.
  • So the advantage of $\mathcal{A}$ is non-negligible even on the condition.

So We need the forger $\mathcal{B}$ to interact with the adversary $\mathcal{A}$ to win the game.

Construction of One-time Forger $\mathcal{B}$:

• Plop $OVK$ into a random leaf $r$.

  1. $\mathcal{B}$ get the one-time verification key $OVK$.

  2. $\mathcal{B}$ generates the pseudorandom signature trees and plop the $OVK$ into a random leaf $r_{OVK}$.

  3. $\mathcal{B}$ sends the root verification key $VK_\epsilon$ to $\mathcal{A}$.

  4. $\mathcal{A}$ requests for the signatures for $q$ times.
     For each message $m_i$, there are two cases.

     1. If $\mathcal{B}$ picks the random leaf $r\ne r_{OVK}$, $\mathcal{B}$ is able to produce the signature.

     2. If $\mathcal{B}$ picks the random leaf $r= r_{OVK}$, $\mathcal{B}$ cannot produce the signature.
        But $\mathcal{B}$ can request the signature for a single message.

        1. $\mathcal{B}$ requests for the message $m_i$.

        2. $\mathcal{B}$ obtains the signature $\sigma_i$ for the single message $m_i$.

        3. $\mathcal{B}$ passes the signature $\sigma_i$ to the $\mathcal{A}$ as the response.

           Note: $\mathcal{B}$ can only picks $r_{OVK}$ once. Besides, it’s necessary to pick it.

  5. $\mathcal{A}$ promises to produce the signature for a new message $m^*\notin \{m_1,m_2,\dots m_q\}$

     • The signature consists of $(r^*,\sigma^*,\text{authentication path for }VK_{r^*})$

     • If $r^*= r_{OVK}$ and $\sigma ^*$ is different from the previous $\sigma_i$ generated by $\mathcal{B}$.

     • Then $\mathcal{B}$ wins. $\mathcal{B}$ just passes the $(m^*,\sigma^*)$ as the forgery signature.

     • But it could happen only if $\mathcal{A}$ picks $r^*$ from one of the leaves $\{r_1,r_2,\dots r_q\}$ given by $\mathcal{B}$.

       Claim :
       If $\mathcal{A}$ picks one of the leaves $\{r_1,r_2,\dots r_q\}$ when forging, then $\mathcal{B}$ can produce the one-time forgery w.p. $1/q$.

But there is no guarantee that $\mathcal{A}$ could pick one of the leaves $\{r_1,r_2,\dots r_q\}$ given from $\mathcal{B}$.

Instead, we plop $OVK$ into a node.

• Plop $OVK$ into the $VK_\epsilon$ location as follows.

  

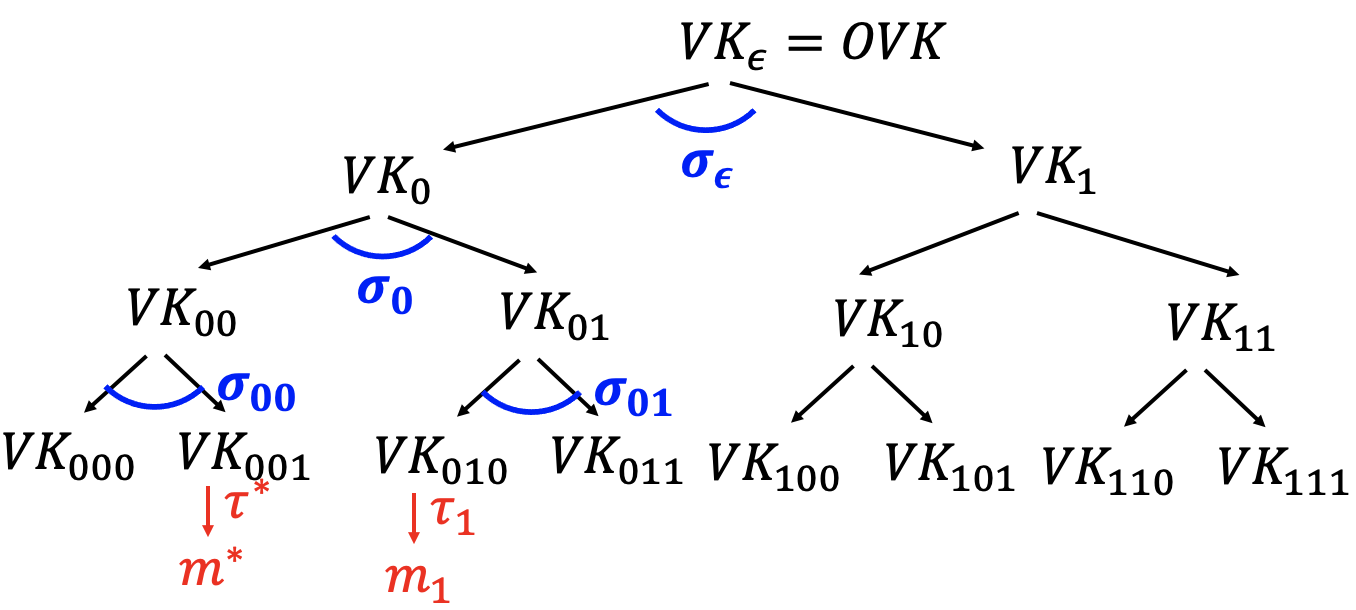
  1. $\mathcal{B}$ get the one-time verification key $OVK$.

  2. $\mathcal{B}$ generates the pseudorandom signature trees and plop the $OVK$ into the root node. So $\mathcal{B}$ knows all secret key except $SK_\epsilon$.

  3. $\mathcal{B}$ sends the root verification key $VK_\epsilon$ to $\mathcal{A}$.

  4. $\mathcal{A}$ requests for the signatures for $q$ times.
     For each message $m_i$, there are two cases.

     1. Pick a random leaf $r$.
     2. Use $VK_r$ to sign $m$.
        $\tau_i\gets Sign(SK_r,m) $
     3. Produce authentication path for $VK_r$.
        Signatures for message $m_1$: $(r,\tau_1,(\sigma_\epsilon,\epsilon_0,\epsilon_{01}))$.
     • $\mathcal{B}$ cannot produce the signature of $\sigma_\epsilon$ since she dosen’t know the $SK_\epsilon$.
     • But $\mathcal{B}$ can request the signature $\sigma_\epsilon$ for a single message $(VK_0||VK_1)$.

  5. $\mathcal{A}$ promises to produce the signature for a new message $m^*\notin \{m_1,m_2,\dots m_q\}$

     • The signature consists of $(r^*,\tau^*,\text{authentication path for }VK_{r^*})$
     • Suppose $\mathcal{A}$ picks $r^*=1$ as above figure.
       The authentication path for $VK_{001}$: $(\sigma_\epsilon’,\sigma_0’,\sigma_{00}’)$.
     • In fact, the output of forgery consists $VK_0’,VK_1’,VK_{00}’,VK_{01}’,VK_{000}’,VK_{001}’$, which could be different from the tree built by $\mathcal{B}$.
     • If $VK_0||VK_1 \ne VK_0’||VK_1’$, $\mathcal{A}$ wins.

• Plop $OVK$ into the $VK_0$ location.
  The analysis is the same.
  If $VK_{00}||VK_{01} \ne VK_{00}’||VK_{01}’$, $\mathcal{A}$ wins.

The main idea is as above.