「Cryptography-MIT6875」: Lecture 12

In this series, I will learn MIT 6.875, Foundations of Cryptography, lectured by Vinod Vaikuntanathan.
Any corrections and advice are welcome. ^ - ^

Topics Covered:

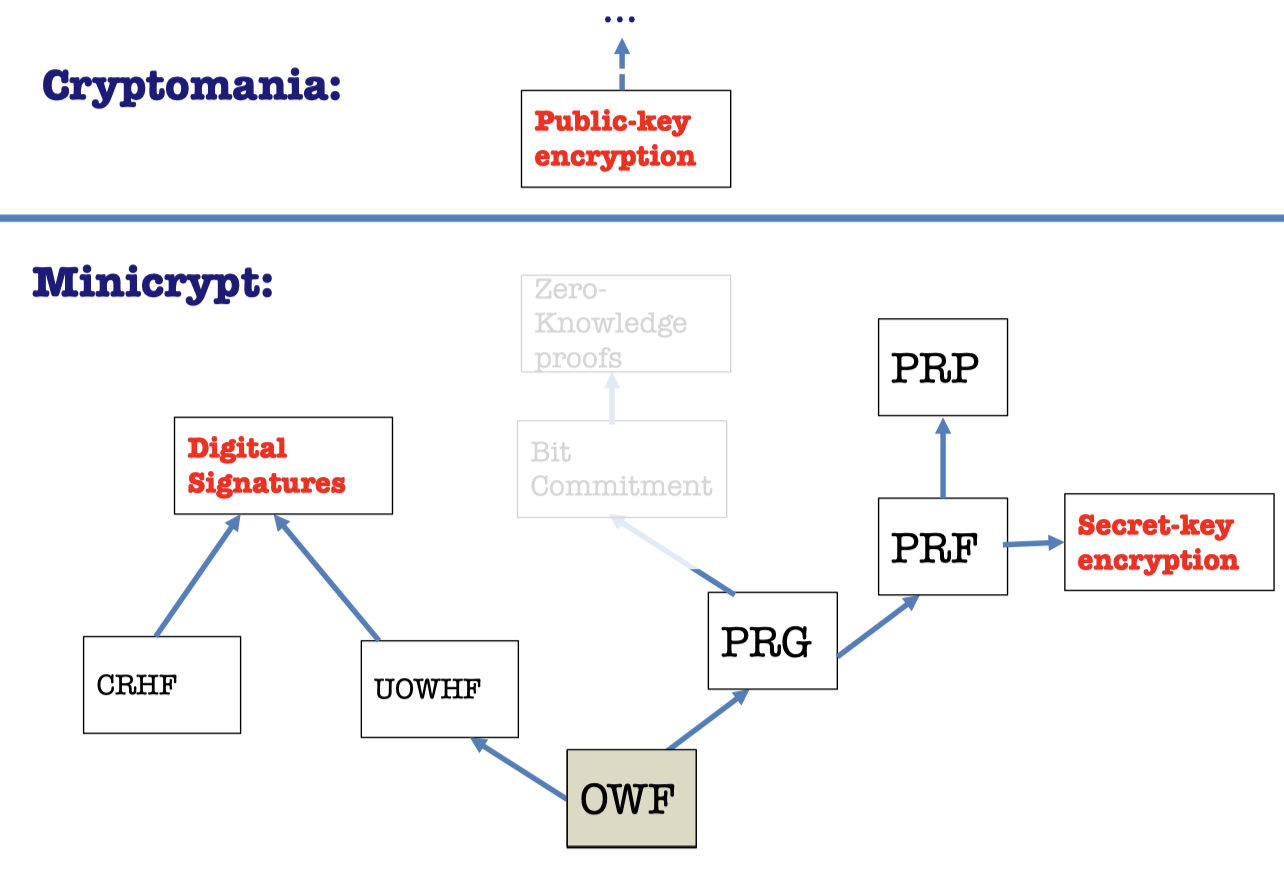
• Construction of CRHF from Discrete Log

• Digital Signatures only from OWF

• Direct Constructions:Trapdoor Permutation and the Hash-and-Sign Paradigm.

• Random Oracles.

Digital Signature from CRHF

We showed the theorem about digital signature in Lecture 10.

Theorem:

Assuming the existence of one-way functions and collision-resistant hash function families, there are digital signature schemes.

CRHF Definition

Recall the definition of Collision-Resistant Hash Functions.

A compressing family of functions $\mathcal{H}=\{h:\{0,1\}^m\rightarrow \{0,1\}^n\}$ (where $m>n$ ) for which it is computationally hard to find collisions.

Definition:

$\mathcal{H}$ is collision-resistant if for every PPT algorithm $A$, there is a negligible function $\mu$ s.t.

$$ \operatorname{Pr}_\mathcal{h\gets H}[A(1^n,h)=(x,y):x\ne y,h(x)=h(y)]=\mu(n) $$

The function $h$ is given to the adversary. And the advantage of finding a collision is negligible.

How can we construct the CRHF ?

Construction of CRHF from Discrete Log

Construction:

• Let $p=2q+1$ be a “safe” prime.
• Let $\mathcal{H}=\{h:(\mathbb{Z}_q)^2\rightarrow QR_p\}$
  • $\mathcal{H}$ maps two element in $\mathbb{Z}_q$ to one element in $QR_p$, the subgroup of quadratic residues in $\mathbb{Z}_p^*$ with order $q$.
  • Each function $h_{g_1,g_2}\in \mathcal{H}$ is parameterized by two generators $g_1$ and $g_2$ of $QR_p$.
• Define $h_{g_1,g_2}(x_1,x_2)=g_1^{x_1}g_2^{x_2} \mod p$.
• This compresses $2\log q$ bits into $\log q\approx \log {q+1}$ bits.

Prove $h_{g_1,g_2}$ is collision-resistant.

Proof:

• Suppose for contradiction that there is an adversary that finds a collision $(x_1,x_2)$ and $(y_1,y_2)$.
• $g_1^{x_1}g_2^{x_2}= g_1^{y_1}g_2^{y_2}\mod p$
• $g_1^{x_1-y_1}= g_2^{y_2-x_2}\mod p$
• $g_1=g_2^{(y_2-x_2)(x_1-y_1)^{-1}}\mod p$ (assuming $x_1-y_1\ne 0$)
• This turns to a discrete log problem of $DLOG_{g_2}(g_1)$.

Turns out to another theorem of digital signature scheme.

Theorem:

Assuming the hardness of the discrete logarithm problem, there are digital signature schemes.

Other Constructions of CRHF

Similarly, we can construct CRHF from the hardness of factoring, lattice problems etc.

It’s not known to follow from the existence of one-way functions or even one-way permutations. It’s still a big open problem.

“Black-box separations”: Certain ways of constructing CRHF from OWF/OWP cannot work.
”Finding collisions on a one-way street”, Daniel Simon, Eurocrypt 1998.

Digital Signature from OWF

But it turns out that collision-resistant hashing is not necessary; something weaker called universal one-way hashing (UOWHF) suffices.

Furthermore, UOWHFs can be constructed from one-way functions alone.

The challenge is different between CRHF and UOWHF.

• CRHF
  1. Give $\mathcal{A}$ the function $h$
  2. It’s computationally hard for $\mathcal{A}$ to gives $(x,y)$ such that $h(x)=h(y)$ s.t. $x\ne y$.
• UOWHF
  1. $\mathcal{A}$ requests for the hash of $x$.
  2. Give $\mathcal{A}$ the hash $h(x)$
  3. It’s computationally hard for $\mathcal{A}$ to give $y$ such that $h(x)=h(y)$ s.t. $x\ne y$.

So we can construct Digital Signature only from OWF.

Theorem:

Digital Signature schemes exist if and only if one-way functions exist.

---

We can construct Digital Signatures from two routes.

• OWF → UOWHF → Digital Signatures
• CRHF(+OWF) → Digital Signatures

Now we catch the sight of words in crypto.

Direct Constructions

We will show that “Hash-and-Sign” is secure in random oracle model.

“Vanilla” RSA Signatures

We can construct Digital Signature scheme directly from any trapdoor permutation, e.g. RSA.

Vanilla RSA Signatures:

• $Gen(1^\lambda)$
  • Pick primes $(P,Q)$ and let $N=PQ$.
  • Pick $e$ relatively prime to $\phi(N)$ and let $d=e^{-1} \pmod {\phi(N)}$.
  • $SK=(N,d)$ and $VK=(N,e)$
• $Sign(SK,m)$
  • Output signature $\sigma=m^d \pmod N$
• $Verify(VK,m,\sigma)$
  • Check if $\sigma^e=m\pmod N$

But it is existentially forgeable and malleable.

Problems:

• Existentially forgeable
  • Attack1: Pick a random $\sigma$ and output $(m=\sigma^e,\sigma)$ as the forgery.
• Malleable
  • Attack2: Given a signature of $m$, you can produce a signature of $2m,3m,\dots$

Fundamental issues under the problems:

1. Can “reverse-engineer” the message starting from the signature. (Attack 1)
2. Algebraic structure allows malleability. (Attack 2)

---

How to fix Vanilla RSA ?

Fixed Vanilla RSA Signature:

• $Gen(1^\lambda)$
  • Pick primes $(P,Q)$ and let $N=PQ$.
  • Pick $e$ relatively prime to $\phi(N)$ and let $d=e^{-1} \pmod {\phi(N)}$.
  • $SK=(N,d)$ and $VK=(N,e,\color{blue}{H})$
• $Sign(SK,m)$
  • Output signature: $\sigma= \color{blue}{H(m)}^d \pmod N$
• $Verify(VK,m,\sigma)$
  • Check if $\sigma^e=\color{blue}{H(m)}\pmod N$

What is $H$ ?

$H$ is some very complicated “hash” function.

$H$ should be at least one-way. ( to prevent Attack 1)

$H$ should be hard to “algebraically manipulate” $H(m)$ into $H(\text{related } m’)$.(to prevent Attack 2)

Collision-resistance dose not seem to be enough.

Given a CRHF $H(m)$, you may be able to produce $H(m’)$ for related $m’$.

The Random Oracle Heuristic

We want a public $H$ that is “non-malleable”.

Given $H(m)$, it is hard to produce $H(m’)$ for any non-trivially related $m’$.

Random Oracle Definition:

For every PPT adversary $A$ and “every non-trivial relation” $R$,

$$
\operatorname{Pr}[A\left(H(m)\right)=H(m’):R(m,m’)=1]=negl(\lambda)
$$

The goal of adversary is to come up with the relation $R$ such that you can somehow manipulate $H(m)$ into $H(m’)$.

How about the relation $R$ where $R(x,y)=1$ if and only if $y=H(x)$ ?

A public $H$ that “behaves like a random function”.

We can consider it as a proxy to a random function.

(A PRF also behaves like a random function, but $PRF_K$ is not publicly computable. )

The adversary $\mathcal{A}$ can get the public function $H$ in reality.

But in the Random Oracle Heuristic world, the only way to compute $H$, virtually a black box, is by calling the oracle.

Claim:

The hashed RSA is EUF-CMA secure in the random oracle model.

Proof:

• Assume there is a PPT adversary $\mathcal{A}$ that breaks the EUF-CMA security of hashed RSA in the random oracle model.

  
  1. Given $\mathcal{A}$ the verification key.
  2. $\mathcal{A}$ asks the Hash Query for poly. times.
     (We can model it to split the hash queries and sign queries.)
  3. $\mathcal{A}$ asks the Sign Query for poly. times.
  4. $\mathcal{A}$ gives a forgery $(m^*, \sigma^*)$.

• Recall the RSA assumption:
  given $N,e$ and $y=x^e\mod N$, hard to compute $x$.

• Then, there is an algorithm $\mathcal{B}$ that solves the RSA problem.

  
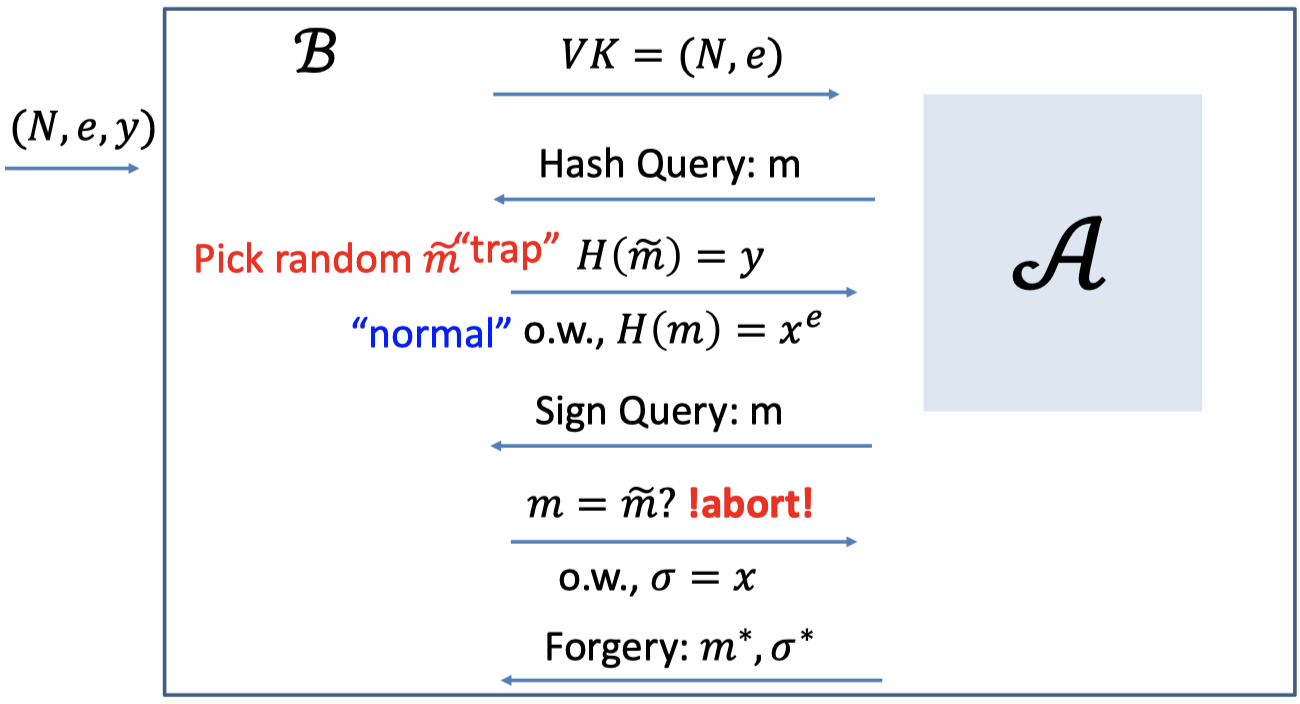
  • The task of $\mathcal{B}$ is to compute $x$ given the $(N,e,y)$.
  • $\mathcal{B}$ needs to interact with the adversary $\mathcal{A}$

  1. $\mathcal{B}$ gives the verification key $VK=(N,e)$ to $\mathcal{A}$.

  2. $\mathcal{A}$ asks polynomially many Hash Queries.

     1. For all hash queries, $\mathcal{B}$ picks a random $\tilde{m}$ as the trap.
     2. For the trap $\tilde{m}$, $\mathcal{B}$ sets the hash $H(\tilde{m})=y$.
     3. For other normal $m$, $\mathcal{B}$ picks a random $x$ and sets the hash $H(m)=x^e$.

  3. $\mathcal{A}$ asks polynomially many Sign Queries.

     For each Sign Query for $m$:

     1. If $m=\tilde{m}$, i.e. hits the trap, $\mathcal{B}$ aborts.
        Because $\mathcal{B}$ cannot produce the signature.
     2. Otherwise, $\mathcal{B}$ is able to produce the signature $\sigma=x$.

  4. $\mathcal{A}$ promises to produce the forgery $(m^*,\sigma^*)$.

     • The thing to notice is that the message $m^*$ is new to all the messages in Sign Query, not in Hash Query.
     • If $m^*=\tilde{m}$, hits the trap, then the signature $\sigma^*=x$ is what she wants.
     • Claim:
       To produce a successful forgery, $\mathcal{A}$ must have queried the hash oracle on $m^*$. With probability $1/q$, $m^*$ is the trap.
       (where $q$ is the number of hash queries)

Bottomline: Hashed RSA (SHA-3)

In practice, we let $H$ be the SHA-3 hash function.

And we believe that SHA-3 acts like a random function.

That’s the heuristic.

On the one hand, it doesn’t make any sense, but one the other hand, it has served us well so far.

There are no attacks against RSA+SHA-3, for example.