「Cryptography-MIT6875」: Lecture 13

In this series, I will learn MIT 6.875, Foundations of Cryptography, lectured by Vinod Vaikuntanathan.
Any corrections and advice are welcome. ^ - ^

Topics Covered:

• Zero knowledge, definitions and example
• ZK Proof for QR Language.
  • honest-verifier ZK
  • malicious-verifier ZK

In the following lectures, we will introduce much more than communicating securely.

• Complex Interactions: proofs, computations, games.
• Complex Adversaries: Alice or Bob, adaptively chosen.
• Complex Properties: Correctness, Privacy, Fairness.
• Many Parties: this class, MIT, the Internet.

Today’s gist is the proof.

It’s very different from the classic proofs.

NP Proofs

In classic proofs, prover writes down a string(proof) and verifier checks.

Little formally, it can be formalized as below.

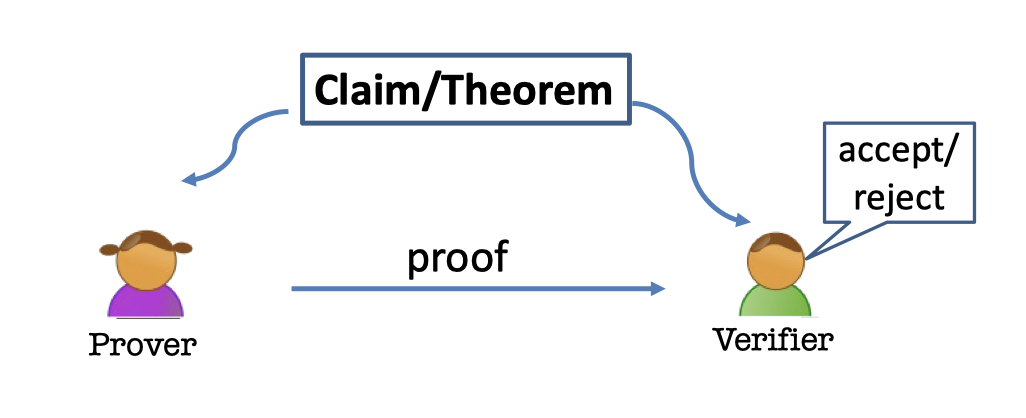
• There is a claim(or theorem), e.g. 15627 is a prime.
• There are two parties, a prover and a verifier.
  • The prover provide a proof to the verifier.
  • The verifier can accept or reject the proof.

NP Language Definition

The proofs of $\mathcal{NP}$ are efficiently verifiable proofs.

Nondeterministic Polynomial-time (NP)

In computational complexity theory, $\mathcal{NP}$ (nondeterministic polynomial time) is a complexity class used to classify decision problems.
$\mathcal{NP}$ is the set of decision problems for which the problem instances, where the answer is “yes”, have proofs verifiable in polynomial time by a deterministic Turing machine, or alternatively the set of problems that can be solved in polynomial time by a nondeterministic Turing machine.

The prover has no computational bounce and needs to work hard to produce a proof.

But the verifier can efficiently verify it in polynomial time.

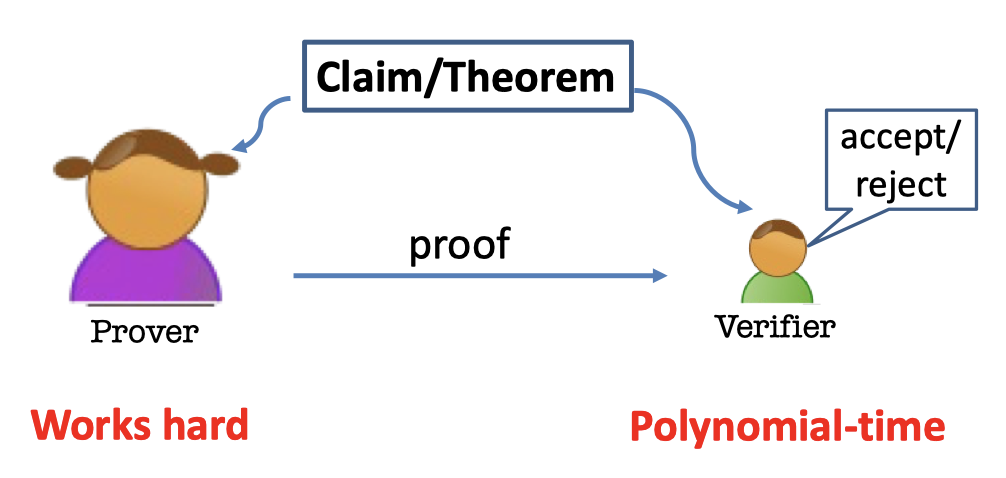
The $\mathcal{NP}$ proof of a theorem is actually a set of strings which can be written down.

Definition of Language Procedure:

A language/decision procedure $\mathcal{L}$ is simply a set of strings. So $\mathcal{L}\subseteq \{0,1\}^*$.

The language is actually a set of strings which represent the true statements.

Definition of $\mathcal{NP}$-language:

$\mathcal{L}$ is an $\mathcal{NP}$-language if there is a poly-time verifier $V$ where

• Completeness: True theorems have (short) proofs.
  For all $x\in \mathcal{L}$, there is a $\texttt{poly}(|x|)\texttt{-long}$ witness (proof) $w\in\{0,1\}^*$ s.t. $V(x,w)=1$.
• Soundness: False theorems have no short proofs.
  For all $x\notin \mathcal{L}$, there is no witness. That is, for all polynomially long $w\in\{0,1\}^*$ s.t. $V(x,w)=0$.

Look at some examples.

e.g.1 N=PQ Language

Theorem: $N$ is a produce of two prime numbers.

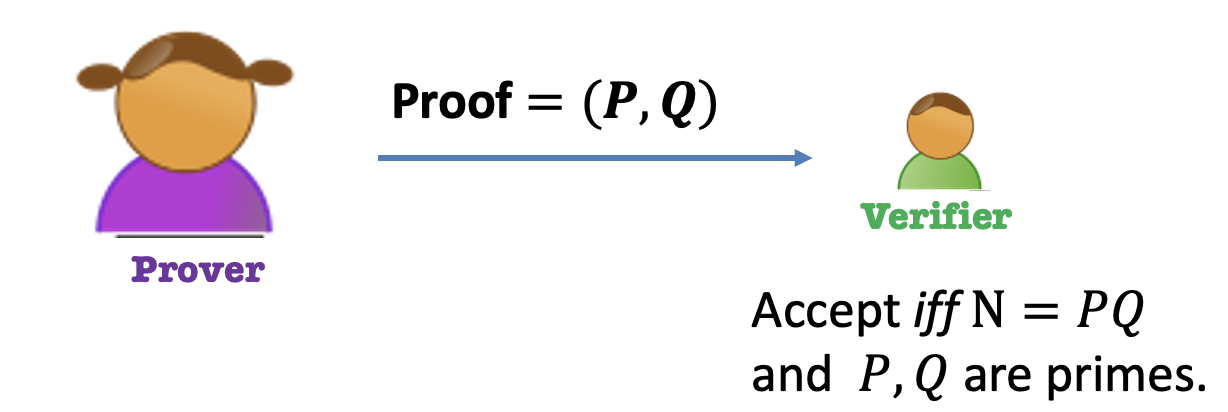
• Prover: Give the two prime factors as proof. $=(P,Q)$.

• Verifier: Accept if and only if $N=PQ$ and $P,Q$ are primes.

• After interaction, Bob, the Verifier knows

  1. $N$ is a produce of two primes.
  2. Also, the two factors of $N$.

e.g.2 QR Language

Theorem: $y$ is a quadratic residue $\mod N$ where $N=PQ$.

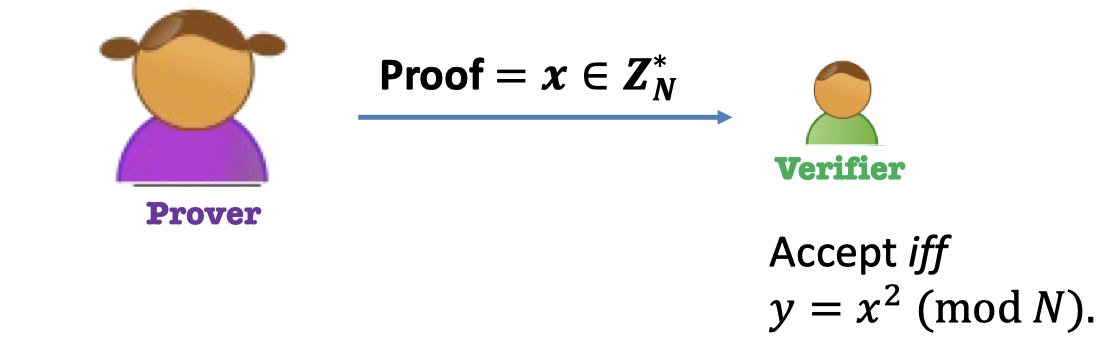
• Prover: Give the square root as proof. $=x$

• Verifier: Accept if and only if $y=x^2\mod N$.

• After interaction, Bob, the Verifier knows

  1. $y$ is a quadratic residue $\mod N$.
  2. Also, the square root of $y$.

e.g.3 Graph Isomorphism Language

Graph Isomorphism Problem

Two graphs $G_0$ and $G_1$ are isomorphic graphs if they have the same number of vertices, edges and also the same edge connectivity.

The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.
The problem is not known to be solvable in polynomial time nor to be NP-complete, and therefore may be in the computational complexity class NP-intermediate.

Theorem: Graphs $G_0$ and $G_1$ are isomorphic.

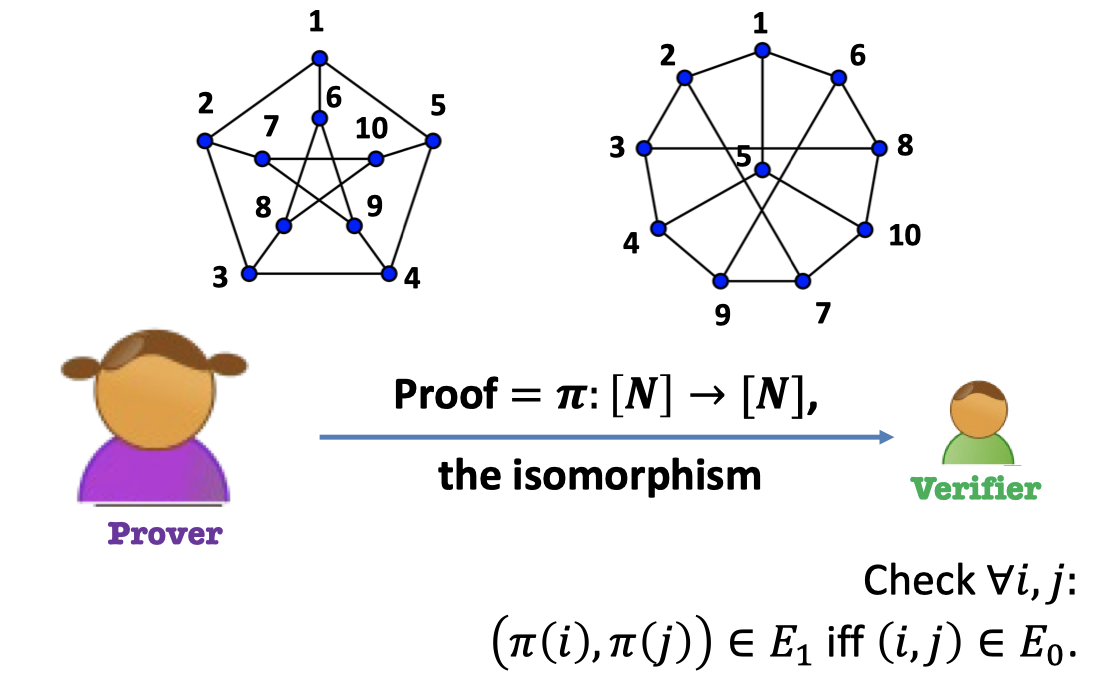
• Prover: Give the map of nodes as proof. $=\pi$

• Verifier: Accept iff the edge connectivity is retained after mapping.

• After interaction, Bob, the Verifier knows

  1. $G_0$ and $G_1$ are isomorphic.
  2. Also, the isomorphism.

e.g.4 Hamiltonian Cycle Language

Hamiltonian Path Problem and Hamiltonian Cycle Problem

A Hamiltonian path is a path that visits each vertex exactly once.
A Hamiltonian cycle is a closed loop on a graph where every vertex is visited exactly once.

In the mathematical field of graph theory the Hamiltonian path problem and the Hamiltonian cycle problem are problems of determining whether a Hamiltonian path or a Hamiltonian cycle exists in a given graph.

Both problems are NP-complete.

Theorem: Graph $G$ has a Hamiltonian cycle.

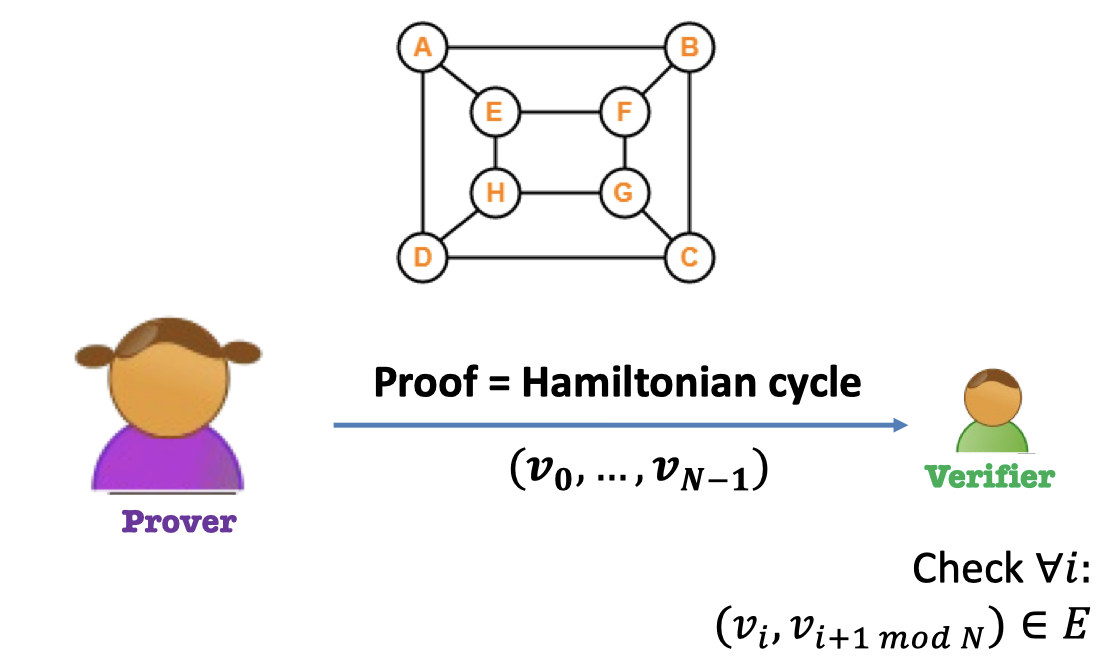
• Prover: Give the Hamiltonian circle as proof.

• Verifier: Accept iff every edge exists.

• After interaction, Bob, the Verifier knows

  1. $G$ has a Hamiltonian cycle.
  2. Also, the Hamiltonian cycle itself.

---

Every one of the above can be reduced to $\mathcal{NP}$-Complete Problem.

Besides, every proof above leaks some valuable information more than the proof itself.

Is there any other way that the prover only tells the verifier whether $y$ is quadratic residue without telling the square root?(Example 2)

The point is that we want to reveal the minimal information.

Interactive Proofs

Before proceeding to Zero Knowledge Proof, let’s start with Interactive Proofs.

Interactive Proof is not a monologue but a dialogue.

There are two necessary new ingredients in Interactive Proofs.

Two (Necessary) New Ingredients:

1. Interaction: Rather than passively reading the proof, the verifier engages in a conversation with the prover.
2. Randomness: The verifier is randomized and can make a mistake with a (exponentially small) probability.

Note: The randomness of the verifier is necessary.

If the verifier is completely deterministic as a function, the prover, since the first message she sends, she knows what the verifier is going to send back.

So she can prepare her second message beforehand, then she can prepare her third message…

It’s not interactive.

The thing to point is that for the prover, she can do no more powerful thing than sending a single message.

Idea

Let’s start with solving the Rubik’s Cube.

Theorem: There is an $\le k$ move solution to this cube.

The idea is split the process of resolving in half.

Interactive Proof:

1. Prover: sends a “random” cube.

   

2. Verify: sends a Challenge (0 or 1)

3. Prover

   1. If Challenge 0: show $k/2$ moves

      

   2. If Challenge 1: show $k/2$ moves

      

The point is that if the prover can do both challenges consistently (or many and many times), then there exists $k$ moves.

We do not take it seriously since there are many flaws in the above protocol.

We just get some inspiration from it.

Definition of IP

The Interactive Proofs for a Language $\mathcal{L}$ is as follows.

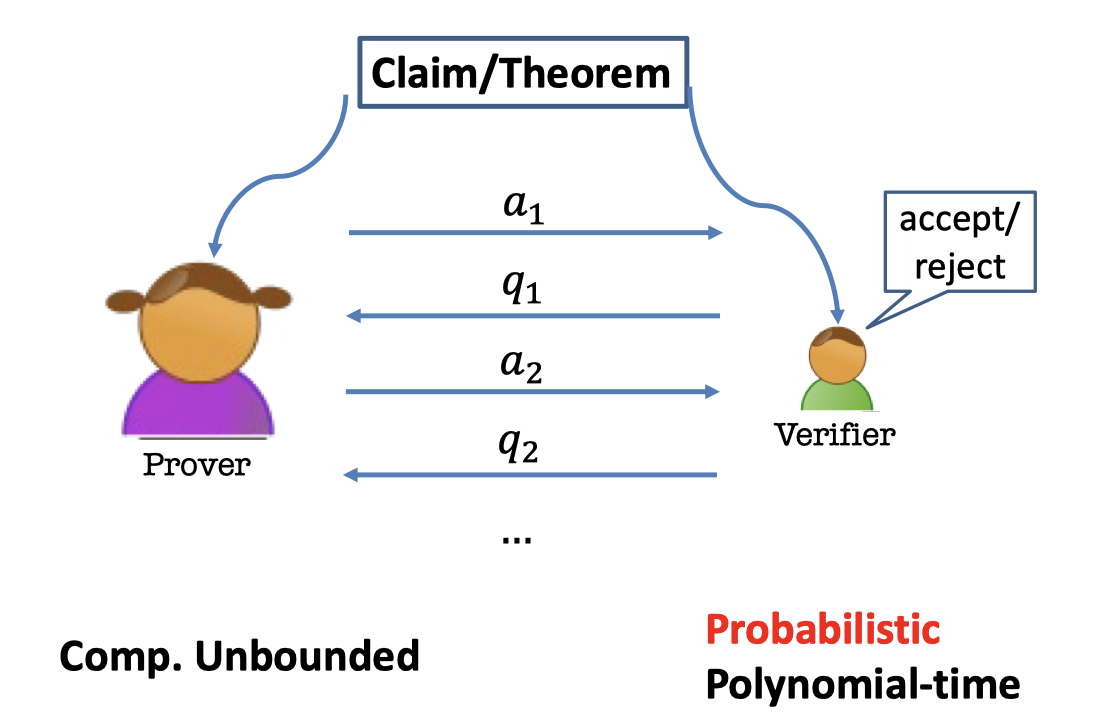
• There is a claim or a theorem.
• Two parties are interacting for a language $\mathcal{L}$.
  • Prover: Computational Unbounded
  • Verifier: Probabilistic Polynomial-time

Definition of $\mathcal{IP}$-Language:

$\mathcal{L}$ is an $\mathcal{IP}$-language if there is a probabilistic poly-time verifier $V$ where
(There are three similar definitions)

• Definition in words.
  • Completeness: If $x\in \mathcal{L}$, $V$ always accepts.
  • Soundness: If $x\notin \mathcal{L}$, regardless of the cheating prover strategy, $V$ accepts with negligible probability.
• Rewrite with probability.
  • Completeness: If $x\in \mathcal{L}$, $\operatorname{Pr}[(P,V)(x)=\texttt{accept}]=1. $
  • Soundness: If $x\notin \mathcal{L}$, there is a negligible function $negl$ s.t. for every $P^*$, $\operatorname{Pr}[(P^*,V)(x)=\texttt{accept}]=negl(\lambda).$
• Relax the probability: Equivalent as long as $c-s\ge 1/poly(\lambda)$
  • Completeness: If $x\in \mathcal{L}$, $\operatorname{Pr}[(P,V)(x)=\texttt{accept}]\color{blue}{\ge c}.$
  • Soundness: If $x\notin \mathcal{L}$, there is a negligible function $negl$ s.t. for every $P^*$, $\operatorname{Pr}[(P^*,V)(x)=\texttt{accept}]\color{blue}{\le s}$.

Completeness is a property of the protocol when $P$ and $V$ are both honest.

Soundness is a property of the protocol when $P$ is dishonest.

So soundness is also a property of the verifier.
The verifier has to be sound because it has to work against an arbitrary $P$.

IP for QR Language

We can give the interactive proof for QR.

$\mathcal{L}=\{(N,y): y \textrm{ is a quadratic residue}\mod N\}$

Interactive Proof:

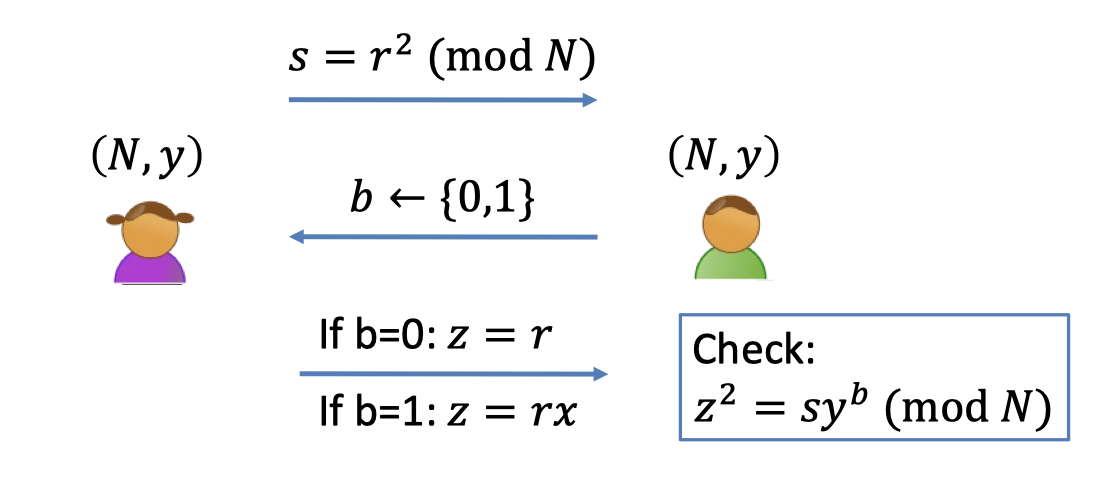
1. Prover: send a random square $s$
2. Verifier: flip a coin $b$ (randomness)
3. Prover
   1. If $b=0$, send $z=r$
   2. If $b=1$, send $z=rx$ where $y=x^2 \mod N$.
4. Verifier: Accept iff $z^2=sy^b \mod N$.

Completeness:

Claim:

If $(N,y)\in \mathcal{L}$, then the verifier accepts the proof with probability 1.

Proof:

• $z^2=(rx^b)^2=r^2(x^2)^b=sy^b$.
• So the verifier’s check passes and he accepts.

Soundness:

Claim:

If $(N,y)\notin \mathcal{L}$, then for every cheating prover $P^*$, the verifier accepts with probability at most $1/2$.

Proof:

• The challenge is random and the randomness is over the coin.

• If the probability equals $1/2$, it means that the cheating prover $P^*$ can only solve one of the challenges, Challenge 0.

• Suppose the verifier accepts with probability $\ge1/2$.

• Then, there is some $s\in \mathbb{Z}_N^*$, the prover is able to pass both challenges.

  So the prover can produce both $z_0$ and $z_1$ beforehand.

  • $z_0:z_0^2=s\mod N$
  • $z_1:z_1^2=sy\mod N$

• This means $(z_1/z_0)^2=y\mod N$, which tells us that $(N,y)\in \mathcal{L}$. (Contradiction)

Moreover, we can make the probability of soundness negligible.

Just *repeat the procedure sequentially $\lambda$ times. *

Claim:

If $(N,y)\notin \mathcal{L}$, then for every cheating prover $P^*$, the verifier accepts with probability at most $(\frac{1}{2})^\lambda$.

Zero Knowledge Proof

Actually, the interactive proof for QR language is Zero-Knowledge.

But what dose zero-knowledge mean?

• After the interaction, $V$ knows:
  • The theorem is true; and
  • A view of the interaction (=transcript + coins of $V$)
    The transcript is all the messages going back and forth.
• $P$ gives zero knowledge to $V$:
  When the theorem is true, the view gives $V$ nothing that he couldn’t have obtained on his own without interacting with $P$.
  • That means the view is not going to give any new knowledge that $V$ couldn’t have it on his own.
  • We can consider the knowledge as some stuff that we cannot generate in probabilistic poly-time on our own.
    If we are given something we can generate by ourselves, it’s zero-knowledge.

$(P,V)$ is zero-knowledge if $V$ can generate his view of the interaction all by himself in probabilistic polynomial time.

$(P,V)$ is zero-knowledge if $V$ can “simulate” his view of the interaction all by himself in probabilistic polynomial time.

We formalize it by the Simulation Paradigm.

The Simulation Paradigm

There are two indistinguishable distributions.

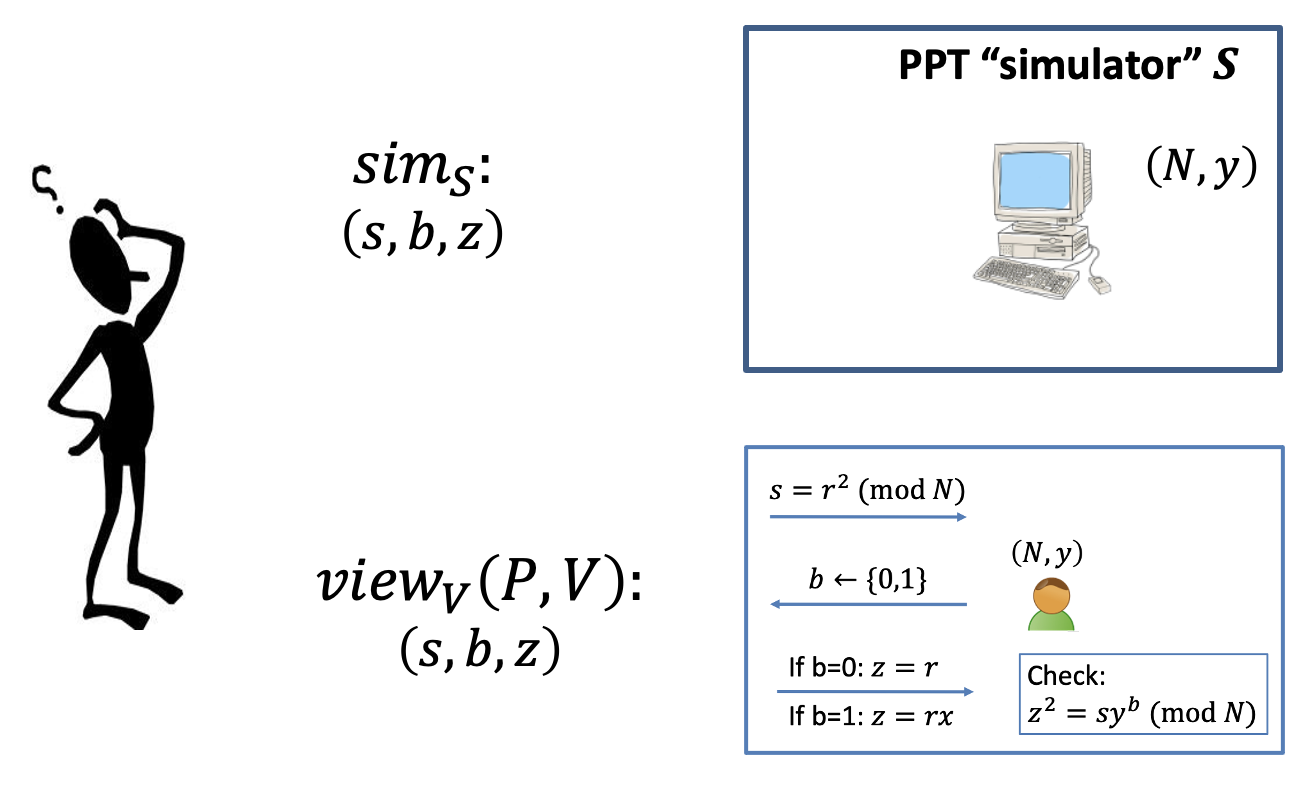
• The real view of the interaction: $\texttt{view}_V(P,V)=(s,b,z$).
  It consists of
  • Transcript: $(s,b,z)$
  • Coins: $b$
• The simulated view: $\texttt{sim}_S(s,b,z)$

We can give the zero-knowledge definition by the simulation paradigm.

Zero-knowledge Definition (for honest V)

(Honest-verifier) Zero-knowledge Definition:

An Interactive Protocol $(P,V)$ is zero-knowledge for a language $\mathcal{L}$ if there exists a PPT algorithm $S$ (a simulator) such that for every $x\in \mathcal{L}$, the following two distributions are indistinguishable.

• $\texttt{view}_V(P,V)$
• $\texttt{sim}_S(x,1^\lambda) $

$(P,V)$ is zero-knowledge interactive protocol if it is complete, sound and zero-knowledge.

• Completeness is a property of the protocol when $P$ and $V$ are both honest.
• Soundness is a property of the protocol when $P$ is dishonest.
  • So it’s also a property of the verifier.
    The verifier has to be sound because it has to work against an arbitrary $P$.
• Zero-knowledge is a property against the verifier.

Actually, we give the definition of zero-knowledge against a honest verifier.

We’ll refine it for any arbitrary verifier in the next section.

There are some analogous definitions of honest-verifier zero-knowledge.

Perfect (Honest-verifier) Zero-knowledge:

An Interactive Protocol $(P,V)$ is perfect (honest-verifier) zero-knowledge for a language $\mathcal{L}$ if there exists a PPT algorithm $S$ (a simulator) such that for every $x\in \mathcal{L}$, the following two distributions are identical.

• $\texttt{view}_V(P,V) $
• $\texttt{sim}_S(x,1^\lambda) $

Statistical (Honest-verifier) Zero-knowledge:

An Interactive Protocol $(P,V)$ is statistical (honest-verifier) zero-knowledge for a language $\mathcal{L}$ if there exists a PPT algorithm $S$ (a simulator) such that for every $x\in \mathcal{L}$, the following two distributions are statistically indistinguishable.

• $\texttt{view}_V(P,V)$
• $\texttt{sim}_S(x,1^\lambda) $

Computational (Honest-verifier) Zero-knowledge:

An Interactive Protocol $(P,V)$ is computational (honest-verifier) zero-knowledge for a language $\mathcal{L}$ if there exists a PPT algorithm $S$ (a simulator) such that for every $x\in \mathcal{L}$, the following two distributions are computationally indistinguishable.

• $\texttt{view}_V(P,V) $
• $\texttt{sim}_S(x,1^\lambda)$

QR Protocol is (honest-V) ZK

Claim:

The QR protocol is (honest-verifier) perfect zero knowledge.

Simulator S works as follows:

1. First pick a random bit $b$.
2. Pick a random $z\in \mathbb{Z}_N^*$.
3. Compute $s=z^2/y^b$.
4. Output $(s,b,z)$.

The simulator can sort of permute things which is offline.

And the verifier is online in the real world.

Lemma:

The simulated transcript is identically distributed as the real transcript in the interaction $(P,V)$.

Proof of Lemma:

• The thing we need to prove is that the distribution of every component in the transcript is identical.
• Real transcript: $\texttt{view}_{V}(P,V)=(s,b,z) $
  • $s$ is square as same as random
  • $b$ is random coin(since the honest verifier)
  • $z=\sqrt{sy^b}$ is random
• Simulated transcript: $\texttt{sim}_S((N,y),1^\lambda)=(s,b,z) $
  • $s=z^2/y^b$ is square as same as random ($(N,y)\in \mathcal{L}$ so $y$ is square)
    Besides, the distribution of $s$ hides $b$ perfectly.
  • $b$ is random
  • $z$ is random
• QED

Actually we only prove the QR protocol is honest-verifier Zero-knowledge.

When the theorem is true, the view gives the honest verifier $V$ nothing that $V$ couldn’t have it on his own.

What if $V$ is NOT honest ?

Note:

The following malicious part is actually lectured in the Lecture 14.
I put it here for the continuous and complete description.

Zero-knowledge Definition (for malicious V)

In real world, the verifier could be malicious that he can do anything he wants.

We hope the view also gives zero-knowledge to the malicious verifier $V^*$.

The definition for honest verifier undermines the definition for malicious verifier.

Recap:

A language $\mathcal{L}$ is actually a set of strings which represent true statements.
The view of $V^*$ is the transcripts and the coins, which contains all the messages going back and forth.

Refine the definitions for malicious verifier $V^*$.

Perfect Zero-knowledge Definition:

An interactive Protocol $(P,V)$ is perfect zero-knowledge for a language $\mathcal{L}$ if for every PPT $V^*$, there exists a (expected) poly time simulator $S$ s.t. for every $x\in \mathcal{L}$, the following two distributions are identical:

• $\texttt{view}_{V^*}(P,V^*) $
• $\texttt{sim}_S(x,1^\lambda)$

Statistical Zero-knowledge Definition:

An interactive Protocol $(P,V)$ is statistical zero-knowledge for a language $\mathcal{L}$ if for every PPT $V^*$, there exists a (expected) poly time simulator $S$ s.t. for every $x\in \mathcal{L}$, the following two distributions are statistical indistinguishable:

• $\texttt{view}_{V^*}(P,V^*) $
• $\texttt{sim}_S(x,1^\lambda) $

Computational Zero-knowledge Definition:

An interactive Protocol $(P,V)$ is computational zero-knowledge for a language $\mathcal{L}$ if for every PPT $V^*$, there exists a (expected) poly time simulator $S$ s.t. for every $x\in \mathcal{L}$, the following two distributions are computationally indistinguishable:

• $\texttt{view}_{V^*}(P,V^*)$
• $\texttt{sim}_S(x,1^\lambda) $

QR Protocol is (malicious-V) ZK

The ZK proof for QR language we gave above is actually honest-verifier zero-knowledge.

In this section, we consider the malicious-verifier zero-knowledge for QR Protocol.

Recap the zero-knowledge proof for QR Language.

$\mathcal{L}=\{(N,y):y \textrm{ is a quadratic residue }\mod N\}$.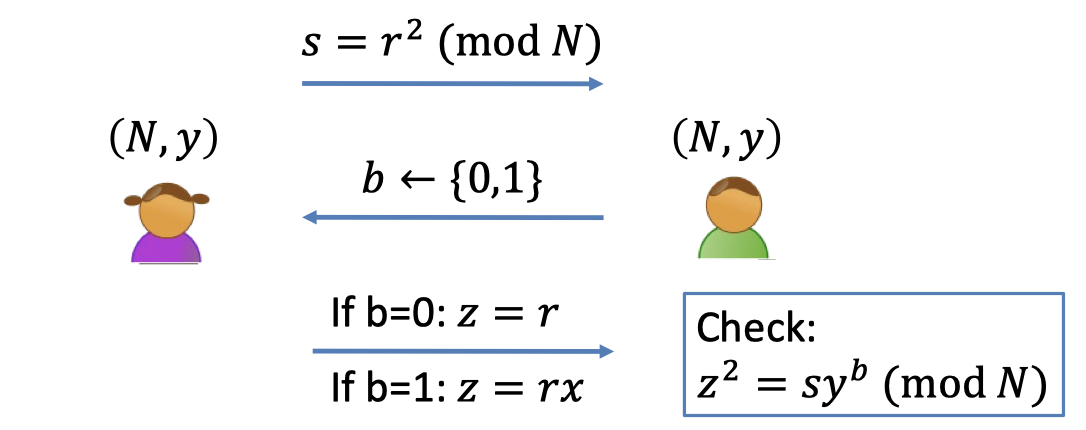

• The view of a malicious verifier $V^*$ is $\texttt{view}_{V^*}(P,V^*)=(s,b,z)$.
  • When $V^*$ obtains the $s$, the only power that $V^*$ has is to choose the $b$ in a bizarre fashion rather than random.
  • So the distribution of $b$ is not random.
  • Let $b=V^*(s)$ denote the bizarre thing generated by $V^*$ after receiving $s$.
• The simulator $S$ only gets an instance of $(N,y)$ and wants to generate $\texttt{sim}_S((N,y),1^\lambda)=(s,b,z)$.

In order to produce the same distribution of $b$, the simulator $S$ needs to interact with the malicious verifier $V^*$.

It’s sort of a prover which also needs to interact with the verifier.

The only distinction is that the prover $P$ has to be online to answer the challenge from the verifier $V^*$ and the simulator $S$ can be offline with the goal of generating the view.

Claim:

The QR protocol is (malicious-verifier) perfect zero knowledge.

Simulator S works as follows:

1. First set $s=z^2/y^b$ for a random $z$ and a random $b$ and “feed” $s$ to $V^*$
2. Let $b'=V^*(s)$. (generated by $V^*$ in any bizarre fashion rather than random)
3. If $b=b’$, output $(s,b,z)$ and stop.
4. Otherwise, go back to step 1 and repeat. (also called “rewinding”)

Lemma:

1. $S$ runs in expected polynomial-time.
2. When $S$ outputs a view, it is identical to the view of $V^*$ in a real execution.

Lemma 1 is well proven.

The probability of terminating in one iteration is $1/2$ since $b$ is random.

So the expected iterations is $2$.

Proof of Lemma 2:

• We need to prove that the distribution of every component is identical.
• Real transcript: $\texttt{view}_{V^*}(P,V^*)=(s,b,z) $
  • $s$ is square as same as random
  • $b$ is generated in any bizarre way, i.e. $b=V^*(s)$.
  • $z=\sqrt{sy^b}$ is random
• Simulated transcript: $\texttt{sim}_S((N,y),1^\lambda)=(s,b,y) $
  • $s=z^2/y^b$ is square as same as random ($(N,y)\in \mathcal{L}$ so $y$ is square)
    Besides, the distribution of $s$ hides $b$ perfectly.
  • $b$ has the same distribution with $b’=V^*(s)$.
  • $z$ is random
• QED

So far we have proven the QR protocol is (malicious-verifier) zero-knowledge.

What made ZK Proof possible ?

1. Each statement had multiple proofs of which the prover chooses one at random.
   (They are $(s,\sqrt{s})$ and $(s,\sqrt{sy})$ as for the QR protocol.)
2. Each such proof is made of two parts (as shown above):
   1. seeing either one on its own gives the verifier no knowledge ;
   2. seeing both imply 100% correctness. (That’s the completeness)
3. Verifier choose to see either part, at random.
   (Verifier can choose to see $\sqrt{s}$ or $\sqrt{sy}$ at random)
   The prover’s ability to provide either part on demand convinces the verify. (That’s the soundness)
   The prover has to prepare both part correctly, otherwise there is a half chance that he’ll get caught.