「Cryptography-MIT6875」: Lecture 15

In this series, I will learn MIT 6.875, Foundations of Cryptography, lectured by Vinod Vaikuntanathan.
Any corrections and advice are welcome. ^ - ^

Topics Covered:

• Sequential vs Parallel Repetition: reduce soundness error
• Proof of Knowledge
  • PoK of DLOG
• Non-Interactive ZK(NIZK)
  • NIZK in The Random Oracle Model
    • NIZK for 3COL
  • NIZK in The Common Random String Model (Lecture 16)

Recap

Recap NP Proofs.

Give NP Proofs for the NP-complete problem of graph 3-coloring.

• Prover $P$: has a witness, the 3-coloring of $G$.
• $P$ gives the proof, the solution to 3-coloring of $G$, to $V$.
• Verifier $V$ checks:
  • only 3 colors are used
  • any two vertices connected by an edge are colored differently.

The verify learned the graph $G$ is 3-colorable and the 3-coloring solution.

So NP proofs reveal too much information.

With Zero-knowledge (Interactive) Proofs, the verifier can only learns the graph $G$ is 3-colorable without knowing the solution.

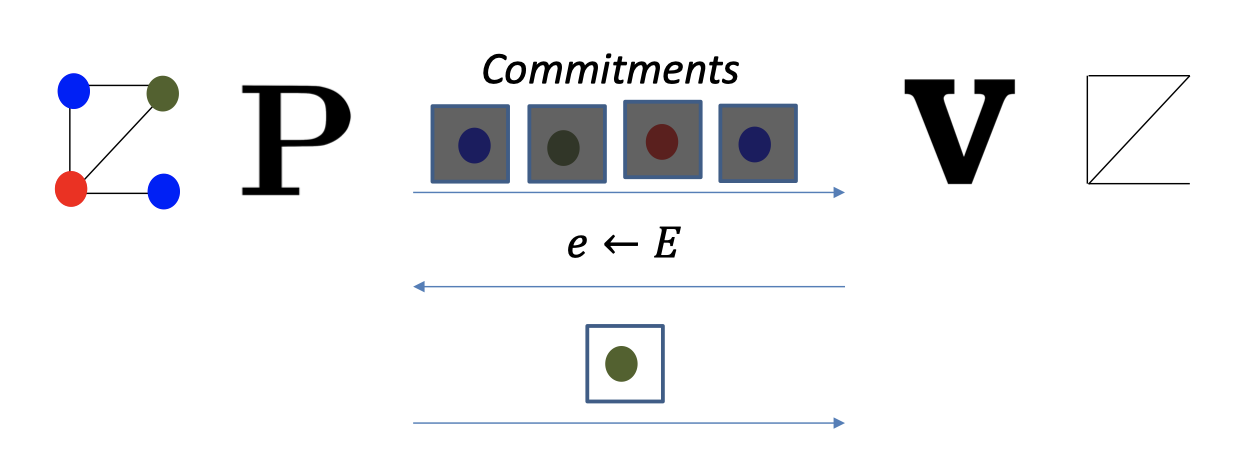
• Prover $P$:
  1. permute the colors
  2. commit to each color
  3. send all the commitments to the verifier.
• Verifier $V$: pick a random edge
• Prover $P$: open the vertices of the edge.
• Verifier $V$ checks the openings & the colorings of two vertices are different.

Besides, we proved the 3COL Protocol is completeness, soundness and zero-knowledge in previous blog.

• Completeness: For every $G\in 3COL$, $V$ accepts $P$’s proof.
• Soundness: For every $G\notin 3COL$ and any cheating $P^*$, $V$ rejects $P^*$’s proof with probability $\ge 1-neg(n)$.
• Zero-knowledge: For every cheating $V^*$, there is a PPT simulator $S$ such that for every $G\in 3COL$, $S$ simulates the view of $V^*$.

Sequential vs Parallel Repetition

The 3COL protocol has a large soundness error of $1-1/|E|$, the probability that $V$ accepts even though $G\notin 3COL$.

Reducing Soundness Error

Theorem:

Sequential Repetition reduces soundness error for interactive proofs, and preserves the ZK property.

But it brings about the problem that it costs a lot of rounds.

An alternative way is parallel repetition.

Theorem [Goldreich-Krawczyk’90]:

Parallel Repetition also reduces soundness error for interactive proofs.

It is also honest-verifier ZK, but dose not, in general, preserve the ZK property.

Note: Preserving the ZK property in general means that it is ZK against malicious verifier.

There is an intuitive interpretation to the theorem.[Goldreich-Krawczyk’90]

The interaction in parallel repetition is $P$ sends all first message in parallel and $V$ response at once with all second messages …

• If $V$ is honest verifier, he indeed dose not look at the commitments, and just picks the random edges independently, which is the same with the sequential repetition.

• But when $V^*$ is malicious verifier, there is no reason that $V^*$ picks the edge independently.
  $V^*$ can apply a giant hash function and do some bizarre thing to pick these dependent edges.

Intuitively, it’s harder to simulate such a thing.

The simulator’s strategy in parallel repetition:

1. $S$ feeds some made up first messages to $V^*$.

2. $V^*$ picks the edges in bizarre manners.

3. $S$ only can answer exactly one challenge.

The key reason is the challenge space is exponentially large and the probability of hitting that made up challenge is negligible.
So this simulation strategy goes down the drain.

This theorem tells that some protocols in parallel repetition is not zero-knowledge against malicious verifier.

And the following theorem tells us that the parallel repetition of 3COL protocol is not zero-knowledge if we run it in many and many times in parallel.

Theorem [Holmgren-Lombardi-Rothblum’s21]:

Parallel Repetition of the (Goldreich-Micali-Wigderson) 3COL protocol is not zero-knowledge.

Fortunately, we have zero-knowledge protocols in const rounds with exponentially small soundness error, rather in a million rounds.

Theorem [Goldreich-Kahan’95]:

There is a constant-round ZK proof system for 3COL (will exponentially small soundness error), assuming discrete logarithms are hard.

Proofs of Knowledge

So far, we focus on the decision problem: $y\in \mathcal{L}$ or $y\notin \mathcal{L}$.

(e.g. $y$ is quadratic residue $\mod N$ or it is not.)

Here is a different scenario that Alice has the knowledge, the discrete log of $y$ assuming $g$ is a generator.

And Alice wants to convince Bob the discrete log of $y$ always exists.

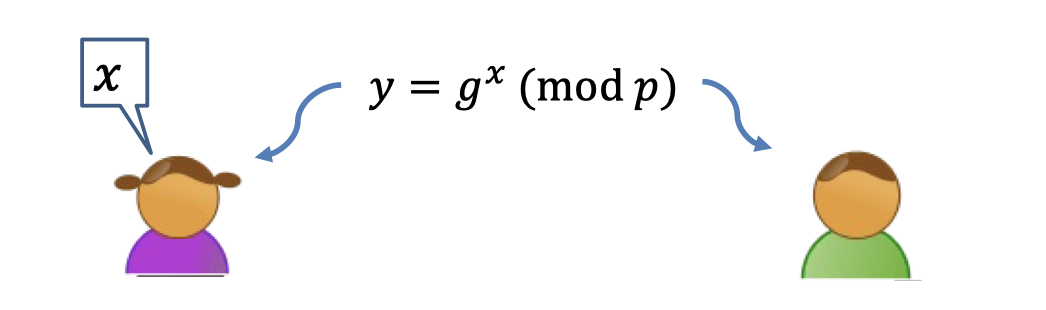
In this scenario the prover wants to convince the verifier that she knows a solution to a problem, e.g. that she knows the discrete log of $y$.

It is difficult to formulate it as the decision problem.

It is Proof of Knowledge.

Likewise, we can define the completeness, soundness and zero-knowledge.

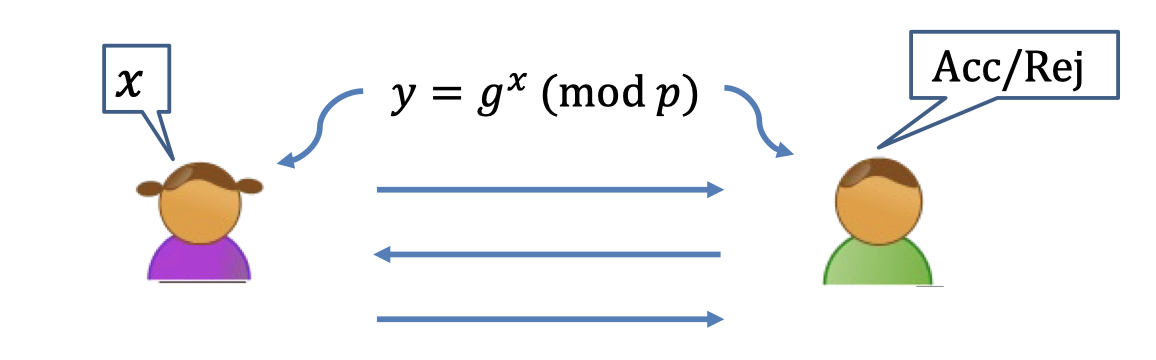
• Completeness: When Alice and Bob run the protocol where Alice has input $x$, Bob outputs accept.
• Soundness: How to define soundness that Alice dose not have the knowledge ?
  It is difficult to formulate the leak of knowledge.
• Zero-knowledge: There is a simulator that, given only $y$, outputs a view of Bob that is indistinguishable from his view in an interaction with Alice.

Extractor

The main idea of Goldreich is that if Alice knows $x$, there must be a way to “extract it from her”.

It’s not about putting diodes on her brain. [*diode 二极管]

It’s sort of talking to Alice.

Definition of Proof of Knowledge:

For any cheating$P^*$, if the prover can convince the verifier that the discrete log of $y$ always exist such that $\operatorname{Pr}[\langle P^*,V\rangle(y)=\textrm{accept}]\ge \varepsilon$, then there exists an extractor $E$ such that $\operatorname{Pr}[E^{P^*}(y)=x \text{ s.t. }y=g^x]\ge \varepsilon'\approx \varepsilon$.

The extractor is indeed the expected ppt adversary.

The definition of PoK is proposed in On Defining Proofs of Knowledge by Mihir Bellare and Oded Goldreich.

We will not dig into the definition but give an example of PoK.

ZK Proof of Knowledge of Discrete Log.

The protocol is as follows.

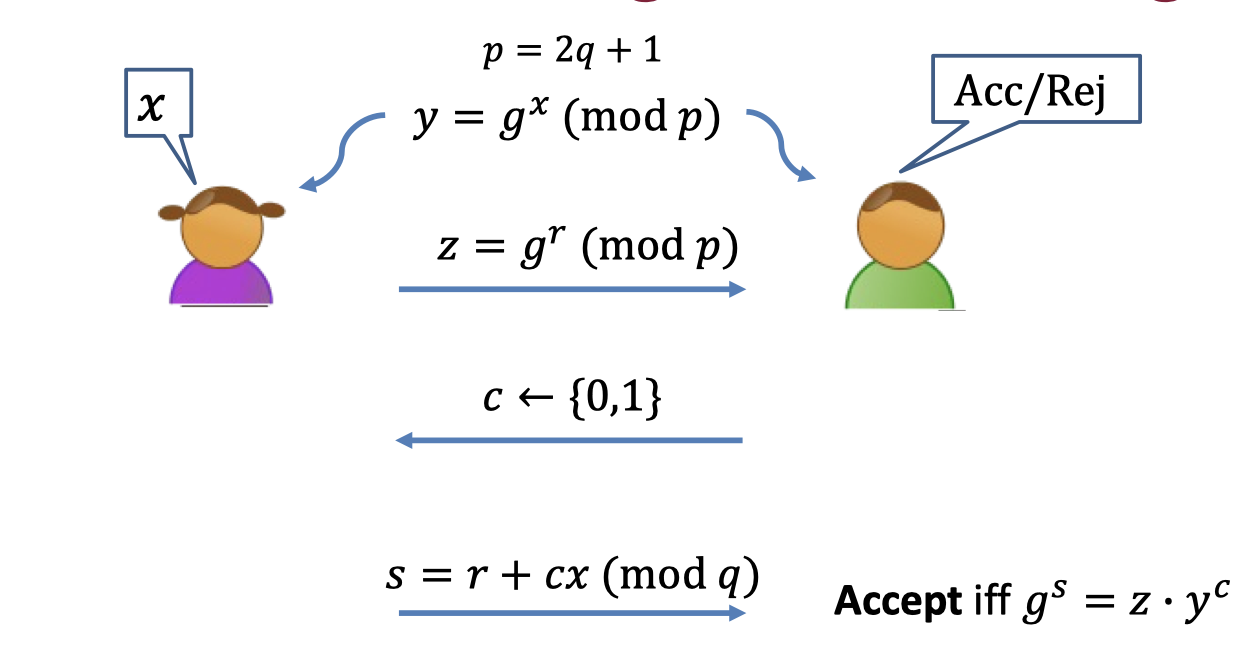
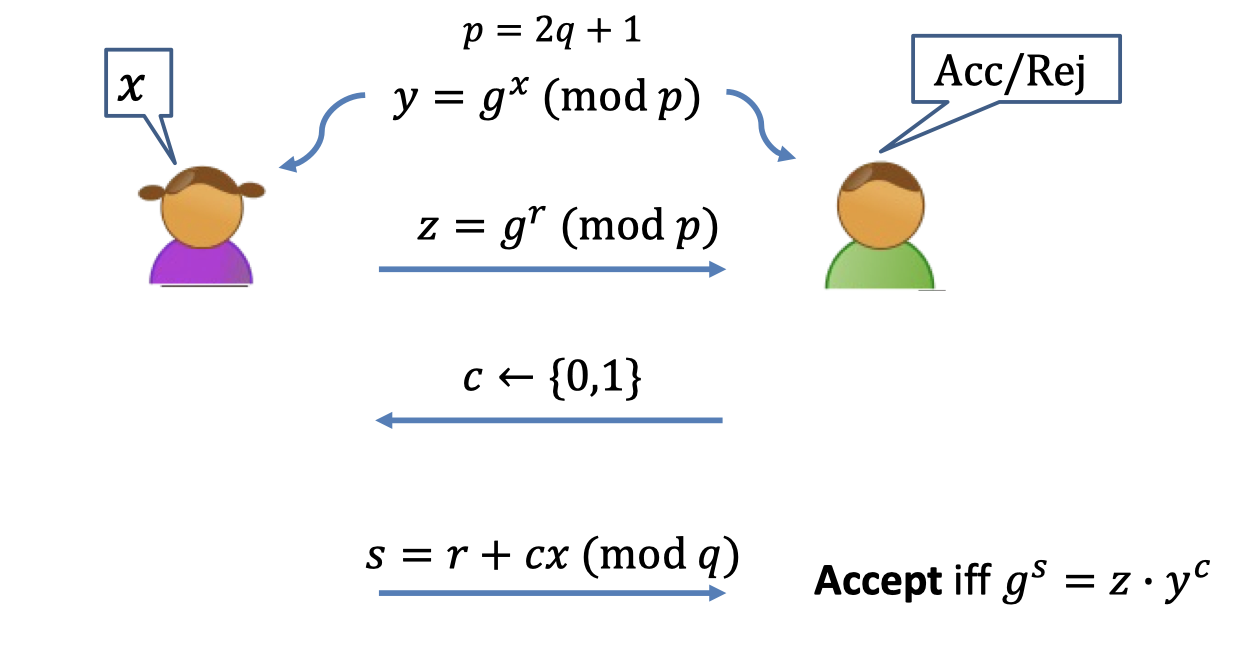
ZK Proof of Knowledge of DLOG:

1. Prover: Pick a random $r$ and send $z=g^r$ to Verifier.
2. Verifier: Pick a random challenge $c$
3. Prover: Answer the challenge
   1. If $c=0$: send $s=r$
   2. If $c=1$: send $s=r+x$
4. Verifier: Accept iff $g^s=z\cdot y^c$.

The above protocol is completeness, soundness and zero-knowledge.

The completeness and zero-knowledge is well proven.

Completeness:

• If the prover has the discrete log of $y$, the verifier accepts with probability 1.
• $g^s=g^{r+cx}=g^r\cdot (g^{x})^c=z\cdot y^c$

Zero-knowledge:

• The real view of $V^*$ is $\texttt{view}_{V^*}=(z,c,s)$
• The simulator works as follows
  1. Generate $z=g^s/y^c$ for a random $s$ and a random $c$.
  2. Feed $z$ to verifier and get the challenge $c^*=V^*(z)$.
  3. If $c^*=c$, output as the simulated transcript.
  4. If $c^*\ne c$, back to step 1 and repeat.
• The simulated view is identical to the view in real execution.

Soundness:

• The key is to construct an extractor by the contradiction.

• If the protocol is of soundness, the cheating prover $P^*$ can convince the verifier with probability $1/2$.

• Assume for the contradiction that $P^*$ convinces the verifier with probability $\ge 1/2+1/poly$.

• Then the prover $P^*$ should prepare for both challenges.

• It’s easy to extract the discrete log of $y$ form $P^*$.

  
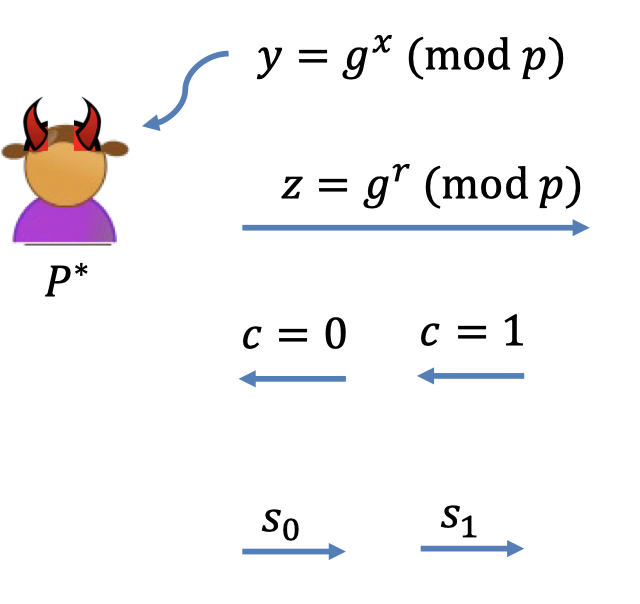
  1. Runs $P^*$ with $c=0$ and gets $s_0$.
  2. Rewind $P^*$ to the first message.
  3. Runs $P^*$ with $c=1$ and gets $s_1$.
  • By contradiction, $g^{s_0}=z$ and $g^{s_1}=zy$ with probability $1/poly$.
  • That is $g^{s_1-s_0}=y$ w.p. $1/poly$.
  • So $s_1-s_0$ is the discrete log of $y$ w.p. $1/poly$.

It’s known as Schnorr proof, or Schnorr Signature.

Efficient Signature Generation by Smart Cards

Non-Interactive ZK

Let’s proceed to the next topic.

Can we make proofs non-interactive again ?

The advantages of Non-Interactive ZK (NIZK):

1. $V$ dose not need to be online during the proof process.
2. Proofs are not ephemeral, can stay into the future.[*ephemeral 短暂的]

NIZK is Impossible

Firstly, we claim that NIZK is impossible.

Suppose there were an NIZK proof system for 3COL.

The NIZK proof is of completeness and zero-knowledge, but NOT sound.

Proof:

1. Completeness: When $G$ is in 3COL, $V$ accepts the proof $\pi$.

   

2. Zero Knowledge: PPT simulator $S$, given only G​ in 3COL, produces an indistinguishable proof $\tilde{\pi}$.
   In particular, $V$ accepts $\tilde{\pi}$.

   

3. Imagine running the Simulator $S$ on a $\underline{G\notin 3COL}$.
   It produces a proof $\tilde{\pi}$ which the verifier still accepts!

   

   Because $S$ and $V$ are PPT.
   They together cannot tell if the input graph is 3COL or not without the witness.

4. Therefore, $S$ is indeed a cheating prover!
   It can produce a proof for a $G\notin 3COL$ that the verifier nevertheless accepts.

   

5. Ergo, the proof system is NOT SOUND.

Two Roads to NIZK

But we can achieve NIZK under some models.

There are two roads to NIZK.

1. Random Oracle Model & Fiat-Shamir Transform
2. Common Random String Model

NIZK: Random Oracle Model

As discussed before randomness of verifier for ZK proofs is necessary.

Otherwise, it is not interactive.

More discussion about randomness.
Give an example in ZK proof of knowledge for discrete log.
The protocol is not sound if $P^*$ knows the random challenge $c$ beforehand.

• If $P^*$ knows $c=0$ beforehand, it’s useless.

• If $P^*$ knows $c=1$ beforehand,

  1. Send $z=g^s/y$ for random $s$.
  2. Send $s$.

NIZK for 3COL

Consider NIZK Proof for 3COL.

Start with the parallel repetition of 3COL protocol.

It is complete, has exponentially small soundness error, and is hones-verifier ZK.

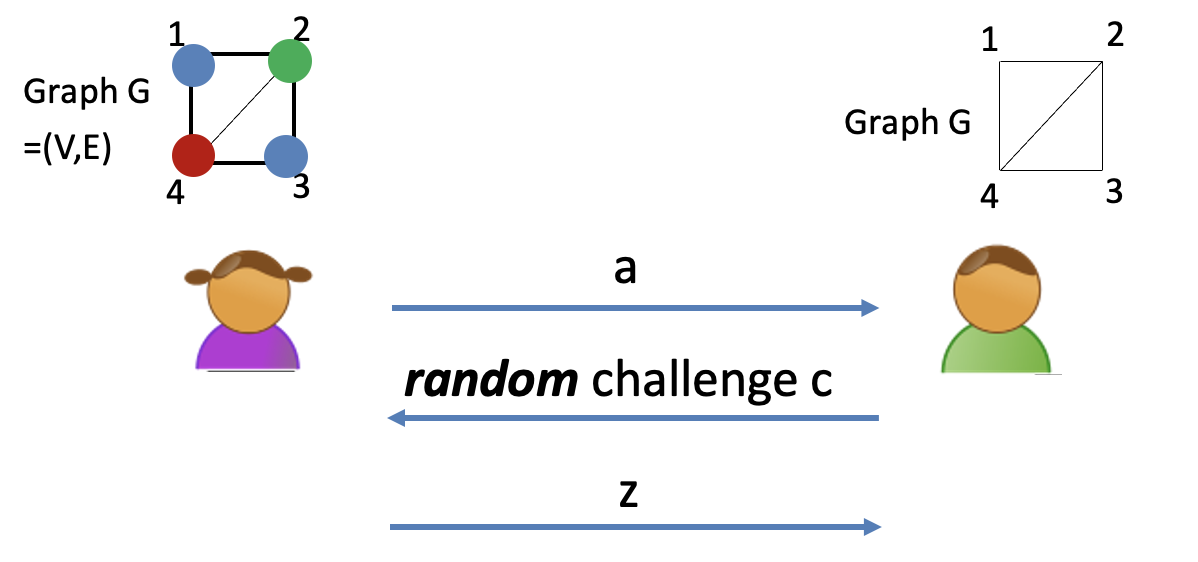
Similarly, the randomness is necessary.

Otherwise, the cheating prover can make up message $a$, $z$ beforehand.

However, the protocol can be non-interactive in the random oracle model.

Recap Random Oracle Model [Lecture 12]

In random oracle model, the only way to compute $H$ is by calling the oracle.
We can consider it as a very complicated public function, e.g. SHA-3.
Moreover, we can consider the public function as a proxy to a random function.

But in the Random Oracle Heuristic world, the only way to compute $H$, virtually a black box, is by calling the oracle.

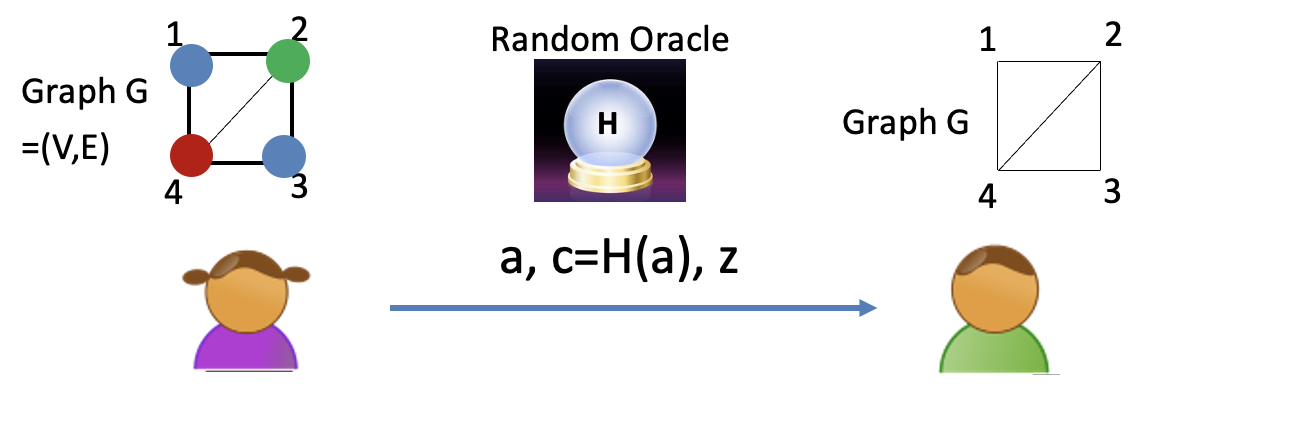
Fiat and Shamir (1986):

Let $c=H(a)$. Now the prover can compute the challenge herself!

It is potentially harmful for soundness.

But in random oracle model for $H$, it can prove soundness.