「Cryptography-MIT6875」: Lecture 17
Any corrections and advice are welcome. ^ - ^
Topics Covered:
- Definition of IND-CCA Security
- Application of NIZK: Construction of CCA-secure encryption scheme
In last post, we saw a NIZK for 3SAT, and then we can get a NIZK for all of NP in the CRS model.
Moreover, we mentioned that if we weaken the notion of proofs into arguments, then we can construct perfect zk for all of NP.
Today, we will discuss the application of NIZK, non-malleable and chosen ciphertext secure encryption scheme.
Active Attacks against CPA-secure Encryption
Recall the public encryption schemes.
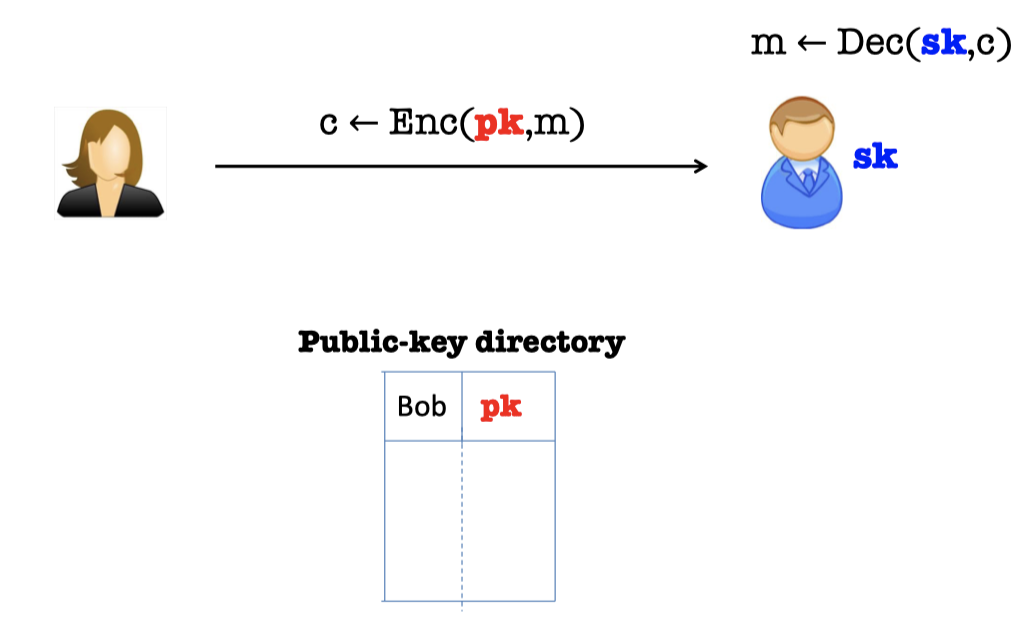
- Bob generate a pair of keys, a public key $pk$, and a private (or secret) key $sk$.
- Bob “publishes” $pk$ and keeps $sk$ to himself.
- Alice encrypts $m$ to Bob using $pk$.
- Bob decrypts using $sk$.
In Lecture 8, we gave the definition of IND-CPA security for public encryption scheme and mentioned the IND-CPA-secure is achievable with randomness.
But there are two active attacks against the public encryption scheme above.
Malleability
The first active attack is malleability.
Consider the scenario for bidding.
Alice wants to bid ¥100 and she encrypts her bid with public key.
There is a malicious attacker that wants to win the bidding and he can modify the encryption of ¥100 into an encryption of ¥101 as his bidding.
The attack can always modify the encryption, which is always one more dollar than Alice’s although the attack dose not know what Alice’s bid is.
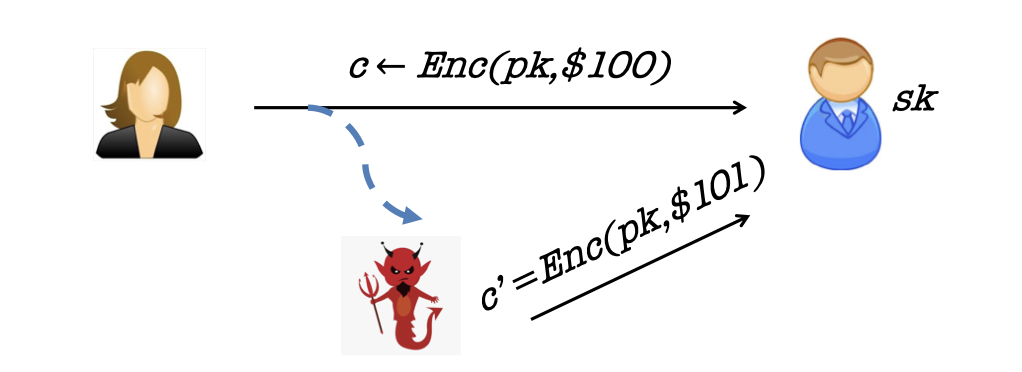
So the adversary could modify (“maul”) an encryption of $m$ into an encryption of a related message $m’$.
Chosen-Ciphertext Attack
Another active attack is chosen-ciphertext attack.
If the first bit of the message is 0, we define it’s the encryption of a valid message.
If the first bit of the message is 1, we define it’s the encryption of an invalid message.
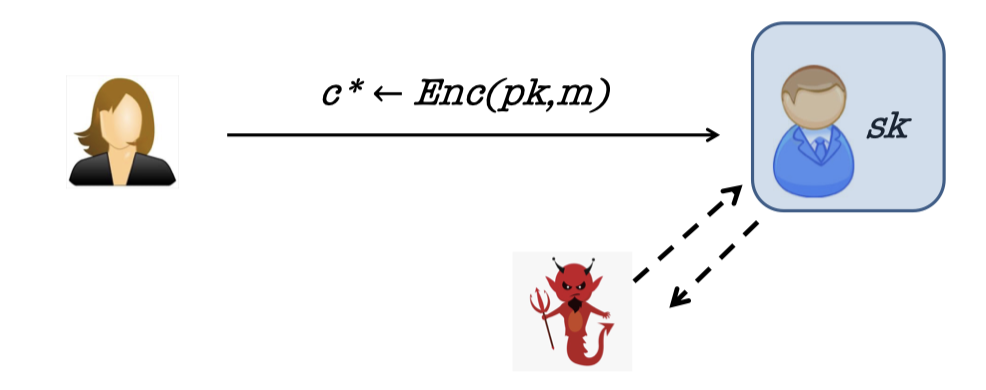
Then the adversary may have access to a decryption “oracle” and can use it to break security of a “target” ciphertext $c^*$ or even extract the secret key!
In fact, Bleichenbacher showed how to extract the entire secret key given only a “ciphertext verification” oracle.
IND-CCA Security
After defining the stronger active attackers, we can define the Indistinguishable Chosen-Ciphertext Attack Security, or IND-CCA.
Recall the game in IND-CPA secure definition.
Game in IND-CPA (one-message):
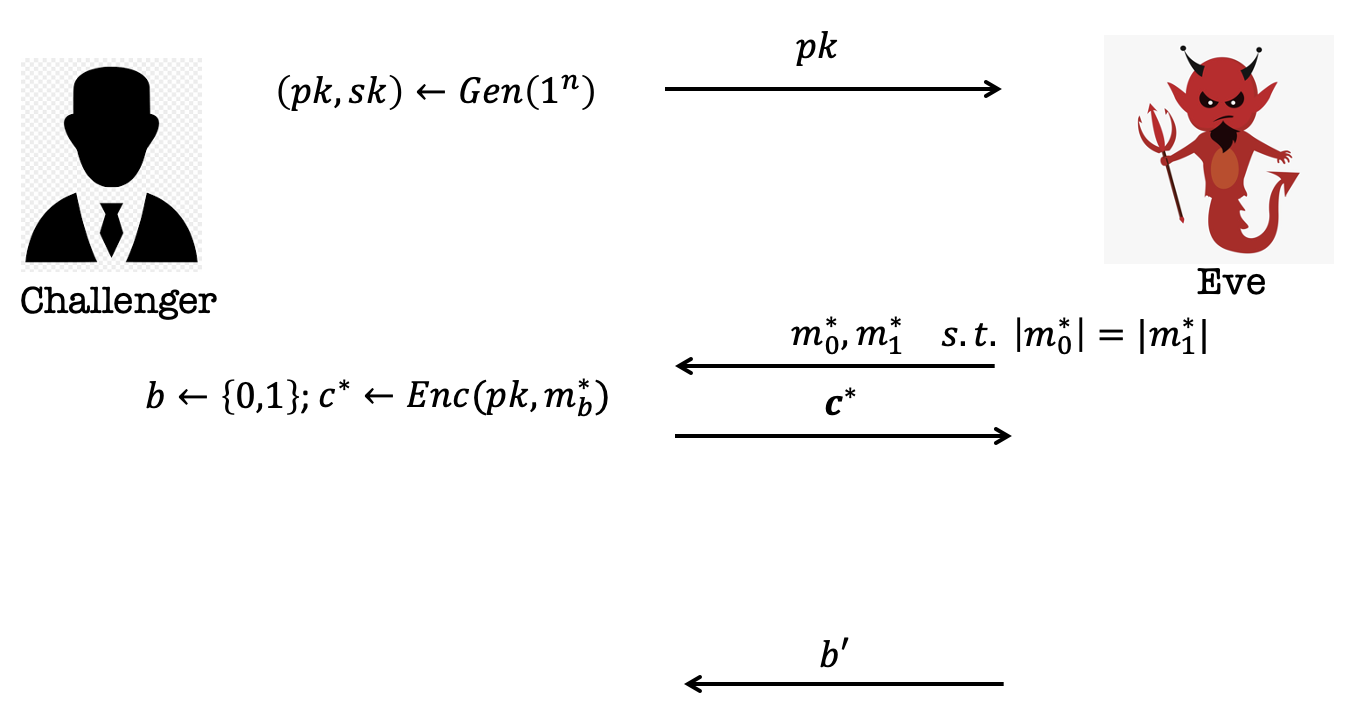
- The Challenger generates a pair of key $(pk, sk)$ and publishes the $pk$.
- Eve sends two single messages, $m_0$ and $m_1$s.t. $|m_0|=|m_1|$.
- The challenger samples $b$ from ${0,1}$ and encrypts the message $m_b$ using $pk$.
And send the ciphertext to Eve. - Eve guesses which message is encrypted and output $b’$.
- Eve wins if $b’=b$.
Let’s move to the game in IND-CCA.
As has been said, the adversary has the power of accessing to a decryption “oracle”.
The adversary can query for the decryption in polynomial many times.
It can happen both before and after the challenge.
Note that the adversary can query for the decryption, before the challenge, of any ciphertext.
But after the challenge, he cannot query for the decryption of the challenge.
Otherwise, the challenge is meaningless.
So there are additional two phases in the game of IND-CCA.
Game in IND-CCA:
- The Challenger generates a pair of key $(pk, sk)$ and publishes the $pk$.
- Eve asks for the decryption of any ciphertext in poly. many times.
- Eve sends two single messages, $m_0$ and $m_1$s.t. $|m_0|=|m_1|$.
- The challenger samples $b$ from ${0,1}$ and encrypts the message $m_b$ using $pk$.
And send the ciphertext to Eve. - Eve asks for the decryption of any ciphertext (except the challenge $c^\star$) in poly. many times.
- Eve guesses which message is encrypted and output $b’$.
- Eve wins if $b’=b$.
IND-CCA Security Definition
The encryption scheme is IND-CCA secure if no PPT Eve can win with probability $>1/2+negl(\lambda)$.
Constructing CCA-Secure Encryption
In the light of the CCA-secure definition, we can construct the CCA-secure encryption scheme.
Our goal is that the adversary is hard to modify an encryption of $m$ into an encryption of a related message, say $m+1$.
Intuitionally, the proof of knowledge and the signatures should help against the malleability for CAP-secure encryption.
With NIZK proofs of knowledge, the idea is that the encryption party attaches an NIZK proof of knowledge of the underlying message to the ciphertext.
Therefore, the encryption consists of CPA-encryption and the NIZK proof of knowledge of the message.
$C:(c=\text{CPAEnc}(m;r),\text{ proof }\pi \text{ that “I know }m\text{ and }r\text{ “})$.
This idea will turns out to be useful, but NIZK proofs themselves can be malleable.
So the active attack turns to create the CPA-encryption of $(m+1,r)$ and the NIZK proof of $(m+1,r)$.
Start with Digital Signatures
Let’s start with digital signatures.
We construct the CCA-secure encryption, which contains the signature of the CPA-secure encryption.
$C:(c=\text{CPAEnc}(pk,m;r),\text{Sign}_{sgk}(c),vk)$
where the encryption produces a signing/verification key pair by running $(sgk,vk)\gets \text{Sign.Gen}(1^n)$.
It is actually not CCA-secure. (or it’s malleable)
If the adversary changes $vk$, all bets are off.
The picture below explains the reason vividly.
Consequently, the lesson is that we need to “tie” the ciphertext $c$ to $vk$ in a “meaningful” way.
IND-CPA → “Different-Key Non-malleability”
One observation is we can reduce IND-CPA to Different-Key Non-malleability(NM).
The Different-Key NM predicates that given (independent) $pk,pk’$ and the encryption $\text{CPAEnc}(pk,m;r)$, the adversary cannot produce $\text{CPAEnc}(pk’,m+1;r)$.
It’s a reduction that suppose the adversary could produce the different-key encryption, then she can break the IND-CPA security of $\text{CPAEnc}(pk,m;r)$.
Proof:
Suppose for contradiction that the adversary has the power of producing the different-key encryption, $\text{CPAEnc}(pk’,m+1;r)$.
The interaction with the Diff-Key NM adversary is as follows.
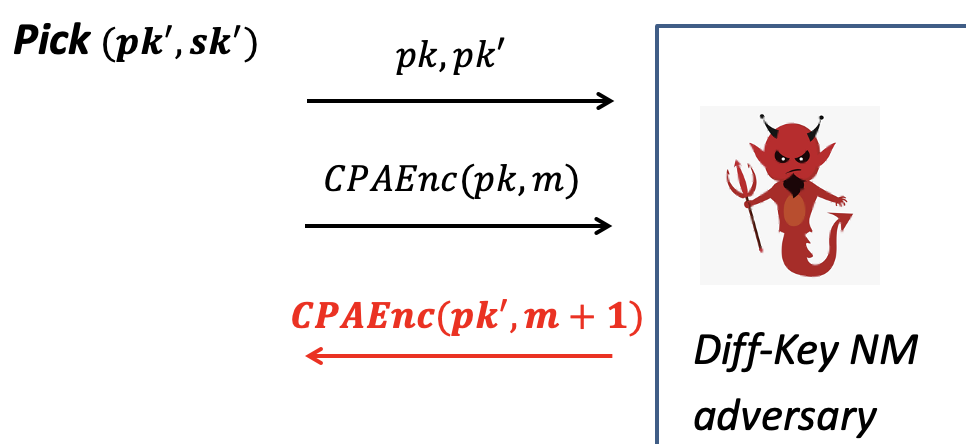
Interaction with Diff-Key NM Adv.
- Pick a random pair $(pk’, sk’)$ and give the two public keys $pk,pk’$ .
- Give the CPA-secure encryption of $m$ using $pk$.
- The Diff-Key NM adv. promises to produce the CPA-secure encryption of $m+1$ using the different key $pk’$. (w.r.t. contradiction)
Then we can construct a CPA adversary by using the Diff-Key NM adversary, as shown below.
Break CPA-secure Encryption
- The challenge is to decrypt the message given CPA-secure encryption.
(as shown on the left of the picture)
- Given $pk$, then we pick a random pair $(pk’,sk’)$ and send $pk,pk’$ to the adversary.
- Give the CPA-secure encryption from CPA challenge.
- The adversary promises to produce an encryption using the different key $pk’$.
- Then we can decrypt it with $sk’$ and subtract 1 to get $m$.
Hence, if the adversary can break the Different-Key NM game, then she can break CPA security.
CCA-Secure Encryption Scheme
We can get non-malleable and CCA-secure encryption putting CPA-secure encryption, digital signature and NIZK proofs together.
As has been said, we need to tie the ciphertext $c$ to the verification key $vk$.
NM Encryption Scheme
CCA Encryption (only non-malleable):
We define $2n$ public keys of the CPA scheme as the CCA public key.
CCA Public Key:
$\left[\begin{array}{llll}p k_{1,0} & p k_{2,0} & \dots & p k_{n, 0} \ p k_{1,1} & p k_{2,1} & \dots & p k_{n, 1}\end{array}\right]$ where $n=|vk|$.
First, pick a signing/verification key pair $(sgk, vk)$.
Then use the CCA public key, based on the bits of $vk$, to produce the ciphertext.
$CT=[ct_{1,vk_1},ct_{2,vk_2},\dots,ct_{n,vk_n}]$ where $ct_{i,j}\gets \text{CPAEnc}(pk_{i,j},m)$.
This ties the ciphertext $CT$ to the verification key $vk$ in meaningful way that the encryption is under the public key indexed by the bits of $vk$.
For each ciphertext in slot $i$ of $CT$:
If the $i$-th bit of $vk$ is 0, then use $pk_{i,0}$ to produce the ciphertext.
If the $i$-th bit of $vk$ is 1, then use $pk_{i,1}$ to produce the ciphertext.
Output $(CT,vk,\sigma=\text{Sign}_{sgk}(CT))$
The encryption scheme above is non-malleable.
Non-malleability rationale:
- If the adversary keeps the $vk$ the same, she needs to produce $(CT’,vk,\sigma_{sgk}(CT’))$ for the related message $m’$, which has to break the signature scheme.
- $CT’$ is encrypted under the same public key as $CT$.
- If the adversary changes the $vk$, she has to break the Different-Key Non-malleability game, and therefore CPA security.
- The adversary needs the produce $(CT’,vk’,\sigma_{sgk’}(CT’))$ for the related message $m’$.
- $CT’$ is encrypted under the different public key, which is indexed by $vk’$.
- Hence, for each different bit of $vk’$:
- The original $ct_{i,j}\gets \text{CPAEnc}(pk_{i,j},m)$.
- The adversary needs to produce $ct_{i,j}’\gets \text{CPAEnc}(pk_{i,1\oplus j},m’)$.
- Turns out the Different-Key NM, which can be reduced to CPA security.
CCA-Secure Encryption Scheme
We are not done!!
Adversary could create ill-formed ciphertexts, e.g. different $ct$s encrypt different messages, and uses it for Bleichenbacher-like attack.
Hence, it has to prove that the ciphertext is well-formed.
CCA Encryption (non-malleable and CCA-secure):
We define $2n$ public keys of the CPA scheme as the CCA public key.
CCA Keys:
PK = $\left[\begin{array}{llll}p k_{1,0} & p k_{2,0} & \dots & p k_{n, 0} \ p k_{1,1} & p k_{2,1} & \dots & p k_{n, 1}\end{array}\right]$, CRS where $n=|vk|$.
SK = $\left[\begin{array}{c}sk_{1,0} \ sk_{1,1}\end{array}\right]$
- To achieve NIZK proof, it has to have (public) CRS.
- The secret key contains only one pair since it needs to be proven well-formed.
First, pick a signing/verification key pair $(sgk, vk)$.
Then use the CCA public key, based on the bits of $vk$, to produce the ciphertext.
$CT=[ct_{1,vk_1},ct_{2,vk_2},\dots,ct_{n,vk_n}]$ where $ct_{i,j}\gets \text{CPAEnc}(pk_{i,j},m)$.
Generate NIZK proof $\pi$ = “CT is well-formed”.
Output $(CT,{\color{blue}\pi},vk,\sigma=\text{Sign}_{sgk}({\color{blue}{CT,\pi}}))$
CCA Decryption:
- Check the signature
- Check the NIZK proof
- Decrypt with $sk_{1,vk_1}$
Now, this encryption scheme is CCA-secure and non-malleable.
Proof of CCA-security:
Proof Sketch
- Suppose for contradiction that there is an CCA adversary.
- Play the CCA game with the adversary.
Note that we will define several hybrid distributions to argument and play the CCA game in one Hybrid. - Then we can use her to break either the NIZK soundness/ZK, the signature scheme or the CPA-secure scheme.
CCA game is as follows.
I drew this picture on my own. since the proof is omitted in the lecture.
Corrections and advice are welcome.
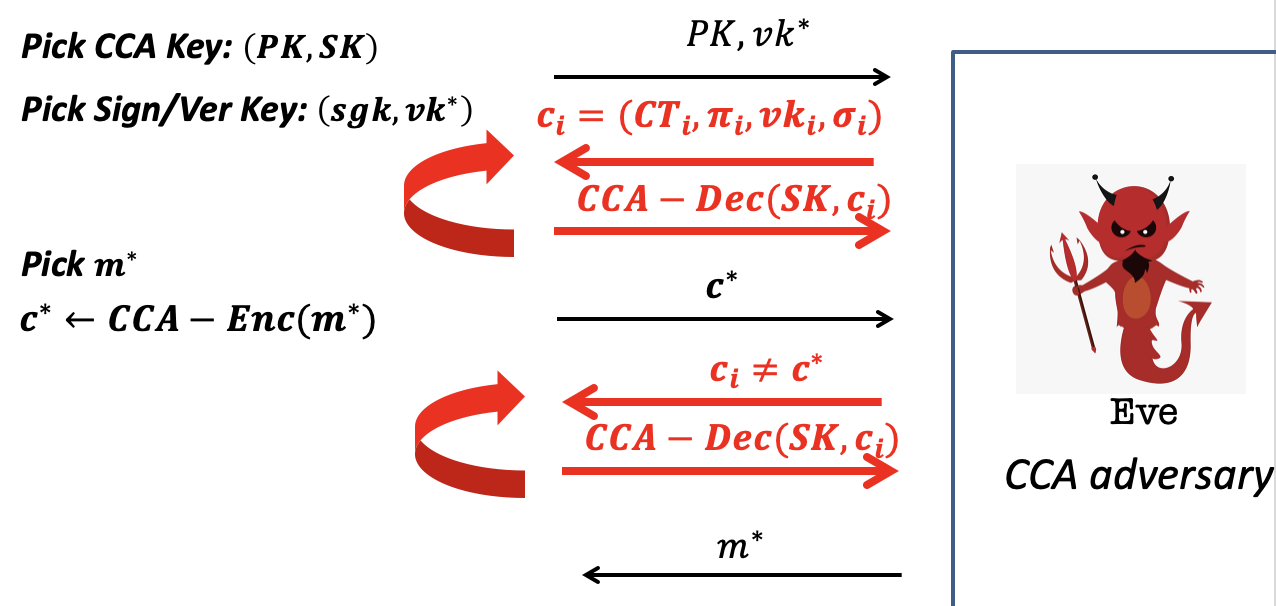
Hybrid 0: Play the CCA game as prescribed.
Hybrid 1: Observe that $vk_i\ne vk^*$. (Otherwise break signature. )
- Observe that this means each query ciphertext-tuple involves a different public-key from the challenge ciphertext.
- Then we can use the “different private-key” to decrypt.
- (If the adversary sees a difference, she broke NIZK soundness.)
It means that the adversary produces a ill-formed ciphertext and she cheats successfuly.
Hybrid 2: Now change the CRS/$\pi$ into simulated CRS/$\pi$. (It’s OK by ZK)
The following proof is my own deduction since the proof is omitted in the lecture.
Corrections and advice are welcome.If we want to use the adversary to break CPA security, it has to win the CPA game as follows.
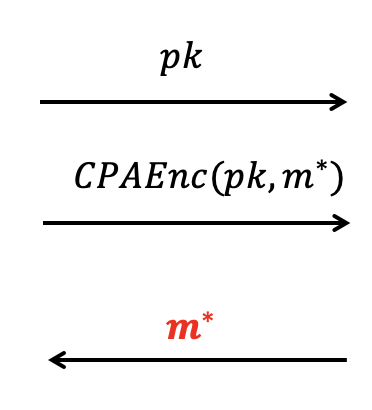
We can plop $pk$, given in CPA game, into one slot of $PK$.
We plop ciphertext, given in CPA game, into $c^*$ with the corresponding slot.
For other slots in $c^*$, we can generate the ciphertext for random message.
But we cannot generate NIZK proof $\pi$ since we don’t have the witness.
It says that the $c^*$ is ill-formed.But we cannot since we don’t have the witness , that is $m^*$, the challenge of CPA game.
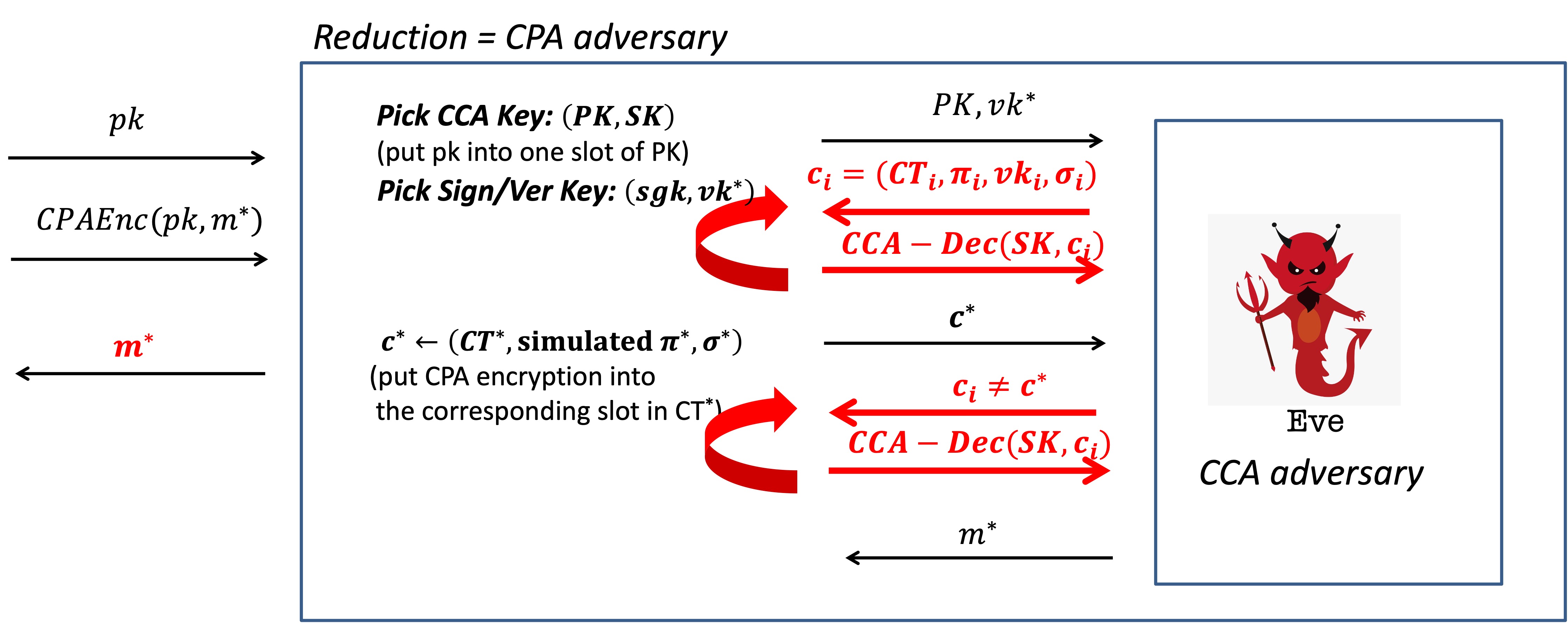
Hence, in Hybrid 2, we change the CRS/$\pi$ into simulated CRS/$\pi$.
It’s zero-knowledge.
But more importantly, we can generate simulated proof.
Consequently, if the adversary wins in this hybrid, she breaks IND-CPA as shown below.
I drew this picture on my own since the proof is omitted in the lecture.
Corrections and advice are welcome.
「Cryptography-MIT6875」: Lecture 17
