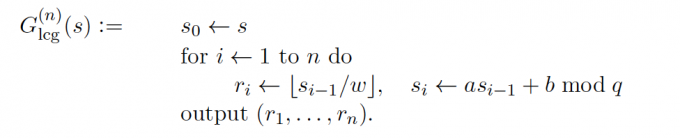「Cryptography-Boneh」:Stream Cipher 1
Stream Cipher的第一部分:介绍了One Time Pad和Stream Cipher中的PRG。
其中OTP部分叙述了什么是Perfect Secrecy?为什么OTP很难在实践中应用?
Stream Cipher部分中,本文主要阐述了什么是PRG?Stream Cipher的另一种安全的定义(依靠PRG的unpredictable)。
本文后半部分,详细阐述了一种weak PRG——线性同余生成器,它是如何工作的?它为什么不安全?如何攻击它?
The One Time Pad
Symmetric Ciphers: difinition
Def :a cipher difined over $\mathcal{(K,M,C)}$ is a pair of “efiicient “ algorithms $(E,D)$ where
$$ E :\mathcal{K \times M \longrightarrow \mathcal{C}} \quad ,\quad D:\mathcal{K\times\mathcal{C}\longrightarrow\mathcal{M}} \\ s.t. \quad \forall m\in \mathcal{M},k\in \mathcal{K}:D(k,E(k,m))=m $$$\mathcal{(K,M,C)}$ 分别是密钥空间、明文空间、密文空间。
对称加密其实是定义在$\mathcal{(K,M,C)}$ 的两个有效算法 $(E,D)$ ,这两个算法满足consistence equation(一致性方程):$D(k,E(k,m))=m$ 。
一些说明:
$E$ is ofen randomized. 即加密算法E总是随机生成一些bits,用来加密明文。
$D$ is always deterministic. 即当确定密钥和明文时,解密算法的输出总是唯一的。
“efficient” 的含义
- 对于理论派:efficient表示 in polynomial time(多项式时间)
- 对于实践派:efficient表示 in a certain time
One Time Pad(OTP)
Definition of OTP
The one time pad(OTP) 又叫一次一密。
用对称加密的定义来表示OTP:
- $\mathcal{M=C=}{0,1}^n\quad \mathcal{K}={0,1}^n$
- $E:\quad c = E(k,m)=k\oplus m \quad$
- $D:\quad m = D(k,c)=k\oplus c$
明文空间和密文空间相同,密钥空间也是n位01串集合。
而且,在OTP中,密钥key的长度和明文message长度一样长。

加密过程如上图所示。
证明其一致性方程
Indeed :
$D(k,E(k,m))=D(k,k\oplus m)=k\oplus (k\oplus m)=0\oplus m=m$
但是OTP加密安全吗?
如果已知明文(m)和他的OTP密文(c),可以算出用来加密m的OTP key吗?
:当然,根据异或的性质,key $k=m\oplus c$
所以什么是安全呢?
Information Theoretic Security
根据Shannon 1949发表的论文,Shannon’s basic idea: CT(Ciphertext) should reveal no “info” about PT(Plaintext),即密文不应该泄露明文的任何信息。
Perfect Security Def:
A cipher $(E,D)$ over $\mathcal{(K,M,C)}$ has perfect security if $\forall m_0,m_1 \in \mathcal{M}\ (|m_0|=|m_1|) \quad \text{and} \quad \forall c\in \mathcal{C} $
$$
Pr[E(k,m_0)=c]=Pr[E(k,m_1)=c] \qquad \text{where} \ k\overset{R}{\longleftarrow}\mathcal{K}
$$
$k \overset{R}\longleftarrow \mathcal{K}$ 的意思是 $k$ 是 从$\mathcal{K}$ 中随机取的,即随机变量 $k$ 的取值是均匀分布。
对任意 $m_0,m_1$ (并且message长度相同),那么在密钥空间任意取 $k$ , $k$ 将 $m_0,m_1$ 加密为相同密文的概率相同。
对attacker来说 :
攻击者截取一段密文c,那么c是由 $m_0,m_1$ 加密而来的概率是相同的,即攻击者也不知道明文到底是 $m_0$ 还是 $m_1$ (因为概率相同)。
$\Rightarrow$ Given CT can’t tell if msg is $m_0 \ \text{or}\ m_1 $ (for all $m_i$ ) .
【攻击者不能区分明文到底是 $m_?$ 】
$\Rightarrow$ most powerful adv.(adversary) learns nothing about PT from CT.
【不管攻击者多聪明,都不能从密文中得到密文的信息】
$\Rightarrow$ no CT only attack!! (but other attackers possible).
【唯密文攻击对OTP无效】
OTP has perfect secrecy
Lemma : OTP has perfect secrecy.
用上一小节的perfect securecy的定义来证明这个引理。
Proof:
要证明: $Pr[E(k,m_0)=c]=Pr[E(k,m_1)=c] \qquad \text{where} \ k\overset{R}{\longleftarrow}\mathcal{K}$
表达式: $\forall m, c: \quad \operatorname{Pr}_{k}[E(k,m)=c]=\frac{\# \text{keys} \ k \in \mathcal{K} \quad s.t.\; E(k,m)=c}{|\mathcal{K}|}$
对于任意m,c, $\operatorname{Pr}_{k}[E(k,m)=c]$ 等于能将m加密为c的密钥个数除以密钥空间的大小。
- $\because |\mathcal{K}|$ 是相同的,所以即证 : $\{ \# \text{keys} \ k \in \mathcal{K} \quad s.t.\; E(k,m)=c \}=\text{const}$
对于任意 m,c,能将m加密为c的OTP key只有一个: $k=m\oplus c$
$\therefore$ OTP has perfect secrecy.
key-len $\geq$ msg-len
Perfect Secrecy的性质带来了一个bad news。
Thm: perfect secrecy $\Rightarrow$ $|\mathcal{K}|\geq|\mathcal{M}|$
如果一个cipher满足perfect secrecy,那么其密钥的长度必须大于等于明文长度。这也是perfect secrecy的必要条件。
所以OTP是perfect secrecy的最优情况,$|\mathcal{K}|=|\mathcal{M}|$ ,密钥长度等于明文长度。
为什么说是一个bad news呢?
如果Alice用OTP给Bob发一段msg,在她发之前,她需要先发一个和msg等长的key,这个key只有Alice和Bob知道。
所以如果Alice有能保密传输key的方法,那她何不直接用这个方法传输msg呢?
所以OTP : hard to use in practice! (long key-len)
因此,我们需要key-len短的cipher。
Pseudorandom Generators(伪随机数生成器)
Stream Ciphers: making OTP practical
Stream Ciphers(流密码)的思想就是:用PRG(pseudorandom Generators) key 代替 “random” key。
PRG其实就是一个function G:${ 0,1 }^s\longrightarrow { 0,1 }^n \quad, n>>s$ 。
通过函数将较小的seed space映射到大得多的output space。
注意: function G is eff. computable by a deterministic algorithm.
- 函数G是确定的,随机的只有s,s也是G的输入。
- PRG的输出应该是 “look random”(下文会提到的PRG必须是unpredictable)
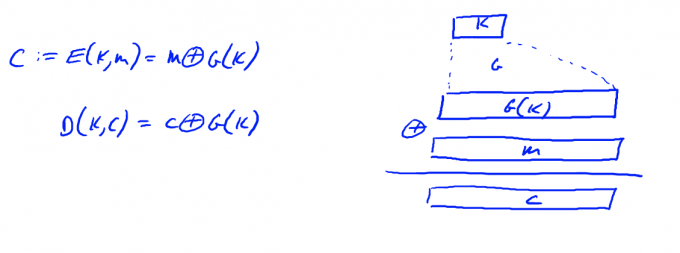
Stream Ciphers的过程如上图所示:通过PRG,将长度较短的k映射为足够长的G(k),G(k)异或m得到密文。
有两个问题?
第一,Stream Cipher安全吗?为什么安全?
第二,Stream Cipher have perfect secrecy?
现在,只能回答第二个问题。
:流密码没有perfect secrecy。因为它不满足key-len $\geq$ msg-len,流密码的密钥长度远小于明文长度。
流密码没有perfect secrecy,所以我们还需要引入另一种安全,这种安全和PRG有关。
PRG must be unpredictable
PRG如果predictable,流密码安全吗?
Suppose predictable
假设PRG是可预测的,即:
$ \exists:\quad G(k)|_{1,2,...,i}\quad \overset{alg.}\longrightarrow \quad G(k)|_{i+1,...,n} $已知G(k)输出的前i bis,存在一种算法,能计算G(k)的后面剩余的bits。
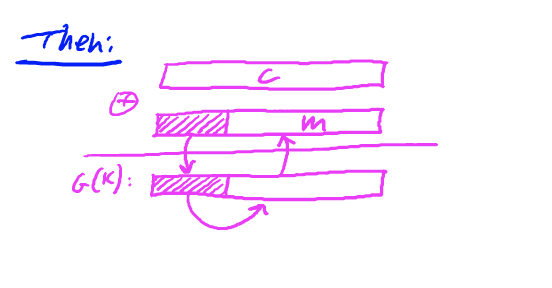
攻击如上图所示:
如果attacker has prior knowledge:已知一段密文前缀的对应明文(m斜线字段)(比如在SMTP协议中,报文的开头总是”from”)
attacker将该密文字段与已知明文字段异或,得到G(k)的前缀。
因为PRG是可预测的,所以可以通过G(k)的前缀计算出G(k)的剩下部分。
得到的G(K)就可以恢复m。
即使,G(k)只能预测后一位,即 $\quad G(k)|_{1,2,...,i}\quad \overset{alg.}\longrightarrow \quad G(k)|_{i+1}$ ,也不安全,当预测出下一位时,又得到了新的前缀,最终得到完整的G(k)。
所以当PRG可预测时,流密码就不安全了。
所以用Stream Cipher时,PRG必须unpredictable!
Predictable: difinition
Predictable Def :
$ \exists $ "eff" alg. A and $\exists$ $0\leq i\leq n-1$ , s.t. $Pr_{k \overset{R}\leftarrow \mathcal{K} } {[A(G(k)|_{1,2,...,i})=G(k)|_{i+1}]}>1/2 +\epsilon$for non-negligible $\epsilon$ (e.g. $\epsilon=1/2^{30}$)
可预测:即存在算法,通过G(k)的前i位可以计算出第i+1位的概率大于1/2 + $\epsilon$ (不可忽略的值)
Unpredictable Def :
即predictable的反面, $\forall i$ : no “eff.” adv. can predict bit(i+1) for “non-neg” $\epsilon$ .
Q:假设 $\mathrm{G}: \mathrm{K} \rightarrow{0,1}^{\mathrm{n}} $ ,满足XOR(G(k))=1,G可预测吗?
W:G可预测,存在i = n-1,因为当已知前n-1位,可以预测第n位。
Weak PRGs
Linear Congruential Generators
一种应该永远不在安全应用中使用PRG——LCG(linear congruential generators)(线性同余随机生成器)。
虽然他们在应用中使用很快,而且其输出还有良好的统计性质(比如0的个数和1的个数基本相等等),但他们应该never be used for cryptographic。
因为在实践中,给出LCG输出的一些连续序列,很容易计算出输出的剩余序列。
Basic LCG
Definition
Basic LCG has four public system parameters:
an integer q, two constants a,b $\in { 0,…,q-1}$ , and a positive integer $w\leq q$ .
The constant a is taken to be relatively prime to q.
【有四个公开参数:整数q,两个q剩余系下的常数a,b,(a与q互素)和一个小于等于q的正整数w。】
We use $\mathcal{S}_q$ and $\mathcal{R}$ to denote the sets: $\mathcal{S}_{q}:=\{0, \ldots, q-1\} ; \quad \mathcal{R}:=\{0, \ldots,\lfloor(q-1) / w\rfloor\}$ Now, the generators $G_{\mathrm{lcg}}: \mathcal{S}_{q} \rightarrow \mathcal{R} \times \mathcal{S}_{q}$ with seed $s\in\mathcal{S}_{q}$ defined as follows: $G_{\operatorname{lcg}}(s):=(\lfloor s / w\rfloor, \quad a s+b \bmod q)$【LCG的输出是一对数,$(\lfloor s / w\rfloor, \quad a s+b \bmod q)$ 】
当 $w=2^t$ 时,$\lfloor s / w\rfloor$ simply erases the t least significant bits of s【右移t位】。
Insecure
当已知 $s^{\prime}:=a s+b \bmod q$ ,即可直接求出s,也就求出了所谓的随机数 $\lfloor s/w\rfloor$ .
Variant: Blum-Micali construction
Definition
如上图所示,变体的LCG是一个迭代,输出不包括 $s_i$ ,把 $r_1,…,r_n$ 作为一次迭代的输出。
不同的应用系统使用不同的 $q,a,b,w$ 参数,在Java 8 Development Kit(JDKv8)中,$q=2^{48}$ , $w=2^{22}$ ,constant $a=\text{0x5DEECE66D}$ , $b=\text{0x0B}$ 。
所以在JDKv8中, LCG的输出其实是 $s_i$(48bits) 的前48-22=26 bits 。
显然JDKv8中的参数大小应用在安全系统中,还是太不安全了。
how to attack in JDKv8
在迭代的第一次输出中,LCG就 reveal 26bits of the seed s。
对于s剩下的后22个bits,attacker can easily recover them by exhausitive search(穷举):
对于每个可能的取值,attacker都能得到一个候选seed $\hat{s}$
用 $\hat{s}$ 来验证我们所直接得到的LCG的输出。
如果 $\hat{s}$ 验证失败,则到第三步继续穷举。直至验证成功。
当穷举至正确的s时,就可以直接预测LCG的剩余输出。
在现代处理器中,穷举 $2^{22}$ (4 million) 只需要1秒。所以LCG的参数较小时,是很容易attack。
当 $q=2^{512}$ 时,这种穷举的攻击方法就失效了。但是有一种对于LCG的著名攻击方法[1],即使每次迭代,LCG只输出较少的bits,也能从这些较少的但连续的输出序列中预测出整个LCG输出序列。
Cryptanalysis :elegant attack
Warning of Math
Suppose
Suppose : q is large (e.g. $q=2^{512}$ ), and $G_{lcg}^{(n)}$ outputs about half the bits of the state s per iteration.
【q很大, $G_{lcg}^{(n)}$ 每次输出s的一半左右的bits】
More precisely, suppose: $w<\sqrt{q}/c$ for fixed c(e.g. $c=32$ )
【保证输出s前一半左右bits的这个条件】
Suppose the attacker is given two consecutive outputs of the gnerator $r_i,r_{i+1}\in \mathcal{R}$ .
【已知两个连续输出 $r_i,r_{i+1}\in \mathcal{R}$ 】
Attacker Knows
$r_{i}=\left\lfloor s_{i} / w\right\rfloor \quad \text { and } \quad r_{i+1}=\left\lfloor s_{i+1} / w\right\rfloor=\left\lfloor\left(a s_{i}+b \bmod q\right) / w\right\rfloor$
【已知: $r_i,r_{i+1},w,a,b,q$;未知: $s_i$ 】
$r_{i} \cdot w+e_{0}=s \quad \text { and } \quad r_{i+1} \cdot w+e_{1}=a s+b+q x \qquad (0\leq e_0,e_1<w<\sqrt{q}/c)$
【 去掉floor符号和mod:$e_0,e_1$ 是 $s_i,s_{i+1}$ 除 $w$ 的余数】
【已知: $r_i,r_{i+1},w,a,b,q$;未知: $s_i,e_0,e_1,x$ 】
re-arranging: put $x$ and $s$ on the left
$s=r_{i} \cdot w+e_{0} \quad \text { and } \quad a s+q x=r_{i+1} w-b+e_{1}$
【把未知参数s,x放在等式左边,方便写成矩阵形式】
$s \cdot\left(\begin{array}{l}1 \ a\end{array}\right)+x \cdot\left(\begin{array}{l}0 \ q\end{array}\right)=\boldsymbol{g}+\boldsymbol{e} \quad \text { where } \quad \boldsymbol{g}:=\left(\begin{array}{c}r_{i} w \ r_{i+1} w-b\end{array}\right) \quad \text { and } \quad \boldsymbol{e}:=\left(\begin{array}{c}e_{0} \ e_{1}\end{array}\right)$
【已知: $\boldsymbol{g},a,q$ ,未知:$\boldsymbol{e},s,x$ 】
to break the generator it suffices to find the vector $\boldsymbol{u}:=\boldsymbol{g}+\boldsymbol{e}$ .
【令 $u\in {Z}^2$ , $\boldsymbol{u}:=\boldsymbol{g}+\boldsymbol{e}=s \cdot(1, a)^{\mathrm{T}}+x \cdot(0, q)^{\mathrm{T}}$ 】
【如果我们求出了 $\boldsymbol{u}$ ,那可以用线性代数的知识解出 $s$ 和 $x$ ,再用 $s$ 来预测PRG的剩下输出】
konws $\boldsymbol{g}$ , knows $\boldsymbol{e}$ is shorter, and $|\boldsymbol{e} |_{\infty}$ is at most $\sqrt{q}/c$ , knows that $\boldsymbol{u}$ is “close” to $\boldsymbol{g}$ .
【e向量很小,$|\boldsymbol{e} |_{\infty}$ 上界是$\sqrt{q}/c$ ,u离g很近】
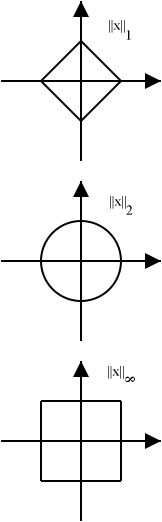
Taxicab norm or Manhattan(1-norm)
${\|}A{\|}_1=\max \{ \sum|a_{i1}|,\sum|a_{i2}|,...,\sum|a_{in}| \}$ (列和范数,A矩阵每一列元素绝对值之和的最大值)Euclidean norm(2-norm)
$\|\mathbf{x}\|=\left(\sum_{i=1}^{n}\left|x_{i}\right|^{2}\right)^{1 / 2}$$\infty$-范数
$\|A\|_{\infty}=\max \{ \sum|a_{1j}|,\sum|a_{2j}|,...,\sum|a_{mj}| \}$ (行和范数,A矩阵每一行元素绝对值之和的最大值)
attack can figure the lattice with attacking LCG.
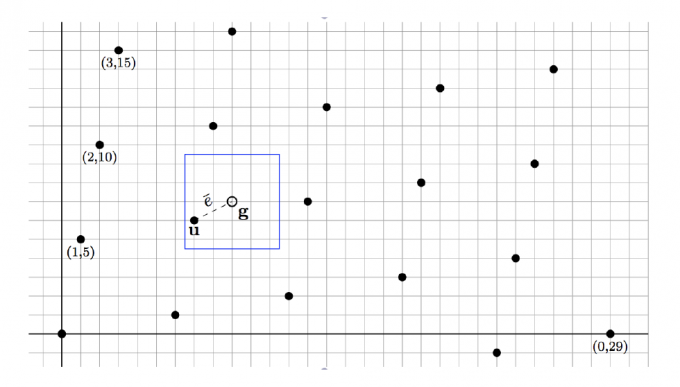
the lattice is generated by the vectors $(1,5)^T$ and $(0,29)^T$ , the attacker has a vector $\boldsymbol{g}=(9,7)^T$ and wishes to find the closest lattice vector $\boldsymbol{u}$ .
【上图是 $(1,5)^T$ 和 $(0,29)^T$ 两个向量生成的的格点,希望能从以上格点找到离已知 $\boldsymbol{g}$ 向量最近的格点】
$\mathcal{L}_a$ :由 $(1, a)^{\mathrm{T}},(0, q)^{\mathrm{T}}$ 作为基向量生成的点集合。
The problem is a special case of a general problem call the closest vector problem: given a lattice $\mathcal{L}$ and a vector $\boldsymbol{g}$ ,find a vector in $\mathcal{L}$ that is closest to $\mathcal{g}$ .
There is an efficient polynomial time algorithm for this problem.[2]
【问题归结于 closest vector problem问题,在已知栅格点集合中找离某一向量最近的点,此问题已有多项式时间算法】
step 8 above
Lemma :
* For at least $(1-16/c^2)\cdot q $ of the a in $\mathcal{S}_q$ , the lattice $\mathcal{L}_a\sub Z_2$ has the following property: for every $\boldsymbol{g} \in Z^2$ there is at most one vector $\boldsymbol{u}\in \mathcal{L}_a$ such that $\|\boldsymbol{g}-\boldsymbol{u}\|_{\infty}<\sqrt{q}/c$ . *
【假设c=32,这个定理表示的意思是:a在$\mathcal{S}_q$ 的所有取值,有98%的取值保证了 $\mathcal{L}_a$ 中离向量 $\boldsymbol{g}$ 最近的点就是我们所求的 $\boldsymbol{u}$ 】
Armed with this algorithm the attacker can recover the internal state $s_i$ of the LCG generator from just two outputs $r_i,r_{i+1}$ of the generator and predict the remaining sequence. This attack works for 98% of the $a\in \mathcal{S}_q$.
【这个定理,可以保证文献中那个多项式算法[2]可以解决98%的a的取值】
For completeness we note that some example $a\in \mathcal{S}_q$ in the 2% where the attack fails are a = 1
and a = 2. For these a there may be many lattice vectors in $\mathcal{L}_a$ close to a given $\boldsymbol{g}$ .
【剩下2%的取值,是a=1,a=2这种取值很小的情况,因为Lattice中格点都离太近了】
Warning of Math!!!(建议清醒的时候看)
Proof of lemma
suppose: there are two vectors $u_0,u_1$ close to $g$ , that is , $\left\|\boldsymbol{u}_{i}-\boldsymbol{g}\right\|_{\infty}<\sqrt{q} / c \text { for } i=0,1$ .
【反证:假设有两个u1,u2离向量g很近,那么u1,u2也离的很近】
- by the triangle inequality, have $\left\|\boldsymbol{u}_{0}-\boldsymbol{u}_{1}\right\|_{\infty} \leq\left\|\boldsymbol{u}_{0}-\boldsymbol{g}\right\|_{\infty}+\left\|\boldsymbol{g}-\boldsymbol{u}_{1}\right\|_{\infty} \leq 2 \sqrt{q} / c$ .
【三角不等式得到, $\boldsymbol{u}_0-\boldsymbol{u}_1$ 的行和范数最大是 $\sqrt{q} / c$ 】
- $\boldsymbol{u}:=\boldsymbol{u}_{0}-\boldsymbol{u}_{1}$ is a vector in $\mathcal{L}_a$ ,and $\mathcal{L}_a$ conclude a "short" vector of non-zero vecor of norm at most $B= 2\sqrt{q} / c$ . Let's bound the number of bad a's for which $\mathcal{L}_a$ contains such a "short vector".
【向量集合的加法封闭性,$\mathcal{L}_a$ 中有一种”short vector”, 他的行和范数最大是$2\sqrt{q} / c$】
【我们去找有多少个”short vector” (number of bad a的最大值),使得有两点$ \boldsymbol{u}_0,\boldsymbol{u}_1$ 都离 $\boldsymbol{g}$ 很近】
set $\boldsymbol{t}=(s, y)^{\mathrm{T}} \in \mathbb{Z}^{2}$ be the “short vector” such that $|t|_{\infty} \leq B$ .
【以下情况讨论可以用一般同余方程 $y=a s(\bmod q)$ 求通解的推导过程来理解】
first consider the case when q is prime.
【先考虑q是素数的情况】
- $\boldsymbol{t}$ 是$\mathcal{L}_a$ 中的点:存在 $s_a,x_a$ 让 $s_{a} \cdot(1, a)^{\mathrm{T}}+x_{a} \cdot(0, q)^{\mathrm{T}}=\boldsymbol{t}=(s, y)^{\mathrm{T}}$ 等式成立。
$\Rightarrow$ $s=s_a$ 和 $y=as_a\pmod{q}$ , 而且 $s\neq0$ 。
$y=as\pmod{q}$ ,由于q是素数, $a$ 可以唯一确定,得到 $a=y s^{-1} \bmod q$ 。
Hence, when q is prime, every non-zero short vector t is contained in at most one lattice $\mathcal{L}_a$ for some $a\in \mathcal{S}_q$ .
【每一个 $\boldsymbol{t}$ 都最多唯一对于 $\mathcal{L}_a$ 中的一个a】
∞-范数的图如下图,所以”short vector” 的个数不超过这个正方形中的格点数,即 $=(2B)^2=16q/c^2$
表述:当 $q$ 是素数时,每一个 “short vector” 对应一个 $a$ 的取值。
表述: $a$ 最多有 $16q/c^2$ 个。
second consider the case when q is not prime.
$y=a s(\bmod q)$ ,q 不是质数,令 $d=\gcd(s,q)$ ,y肯定也是d的倍数
$\Rightarrow y/d=a\cdot s/d \pmod{q/d}$ ,且 $\gcd(s/d,q/d)=1$
$a_0$ 是 $a$ 在 mod $q/d$ 下的逆元。【同余方程的通解推导过程可以去看看】
那么$y/d=a\cdot s/d \pmod{q/d}$ 中解 $a=a_0\cdot y/d$
$y=a s(\bmod q)$ 的通解就是 $a=a_0\cdot y/d + k\times q/d$ ($k=0,1,…d-1$ ) ,解数是 $d$ .
表述:$y$ 最多有 $2B$ 个取值,但是只有 $2B/d$ 个 $y$ 使得方程有解。
表述:所以 $\boldsymbol{t}$向量的 $y$ 值最多只有 $2B/d$ 个。即”short vector” 只有 $2B/d \cdot2B$ 个
表述:每个 $y$ 使方程有解,但其解数是 $d$ 个。即每一个 “short vector” 对应 $d$ 个 $a$ 值。
表述:同样, $a$ 最多有 $16q/c^2$ 个。
综上, $\mathcal{S}_q$ 中最多有 $16q/c^2$ 个 bad $a$ 。
Therefore, for $(1-16/c^2)\cdot q$ of the a values in $\mathcal{S}_q$ , the lattice $\mathcal{L}_a$ contains no non-zero short vectors and the lemma follows.
【证毕】
Reference
LCG的数学部分来自Dan教授密码学的公开书:「A Graduate Course in Applied Cryptography」by D. Boneh and V.shoup
A. M. Frieze, R. Kannan, and J. C. Lagarias. Linear congruential generators do not produce random sequences. In FOCS, pages 480{484, 1984}.
P. C. van Oorschot and M. J. Wiener. Parallel collision search with application to hash functions and discrete logarithms. In Proceedings of the 2nd ACM Conference on Computer and Communications Security, pages 210{218, 1994}.
「Cryptography-Boneh」:Stream Cipher 1