「机器学习-李宏毅」：Tips for Deep Learning

这篇文章中，详尽阐述了在训练Deep Neural Network时，改善performance的一些tips。
tips从Training和Testing两个方面展开。
在Training中结果不尽人意时，可以采取更换新的activation function（如ReLu,Maxout等）和采用Adaptive Learning Rate的GradientDescent算法（除了Adagrad,还有RMSprop、Momentum、Adam等）。
当在Training中得到好的performance，但在testing中perform bad时，即遇到了overfitting，又该怎么处理呢？文章后半部分详尽介绍了EarlyStopping、Regularization和Dropout三个solution。

Recipe of Deep Learning

Deep Learning 的三个步骤：

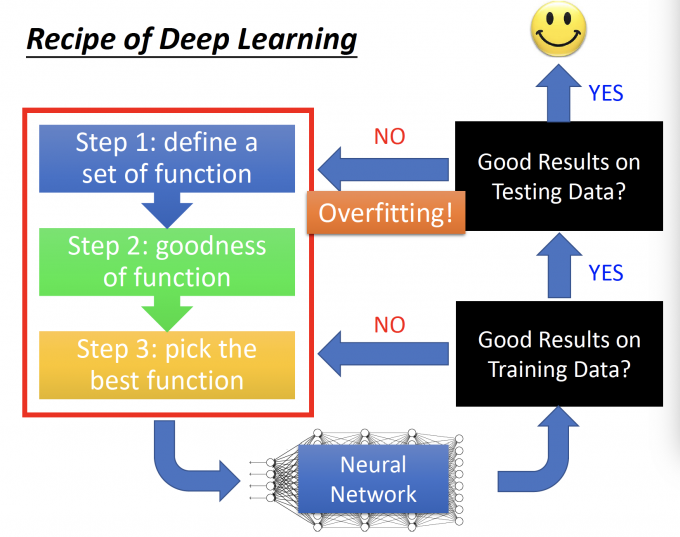
如果在Training Data中没有得到好的结果，需要重新训练Neural Network。

如果在Training Data中得到好的结果，在Testing Data（这里的Testing Data是指有Label的Data，比如Kaggle的Public Data或者是从Training Data中划分出的Development Data）没有得到的好的结果，说明Overfitting了，需要重新设计Neural Network的结构。

Do not always blame Overfitting

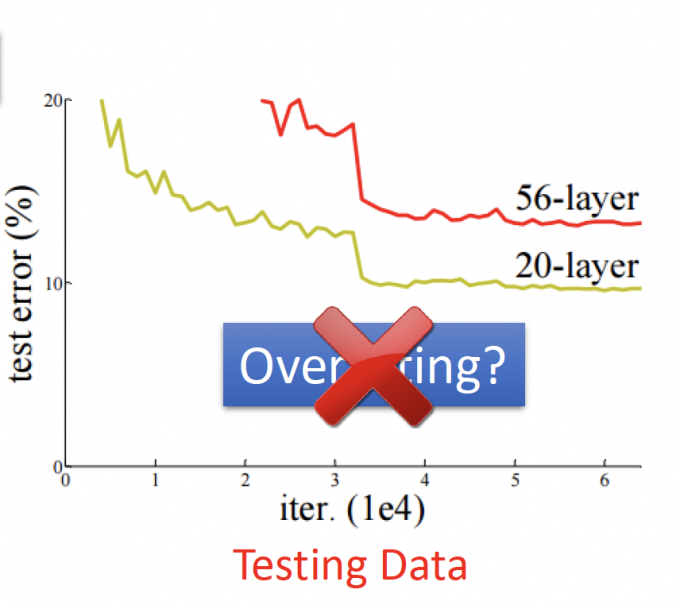
如果在Testing Data中，看到上图，20-layer的error小，56-layer的error大，56-layer一定overfitting了。

No!!!不要总把原因归咎于Overfitting。

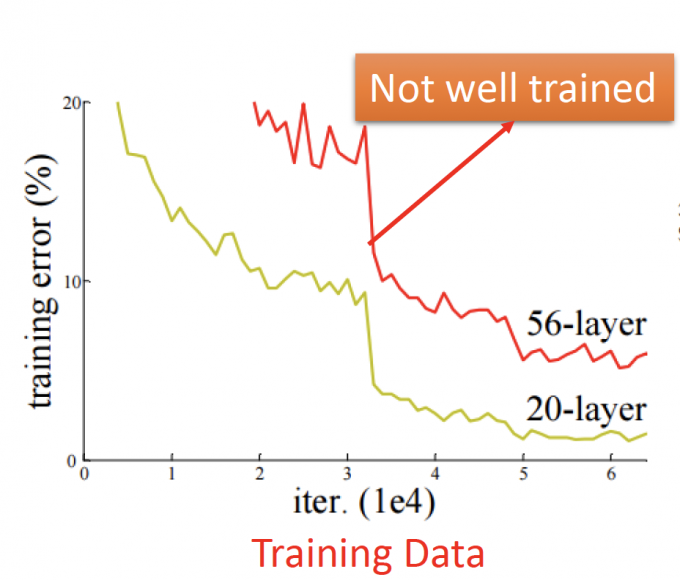
再看Testing Data error之前，先看看Training Data的error。上图中，56-layer的DNN在Training Data的error本来就比20-layer的大，说明56-layer的DNN根本没有train好。

所以56-layer的DNN在Testing Data上的error大，原因不是overfitting，而是模型根本没有train好。

注： Overfitting是在Training Data上error小，但在Testing Data上的error大。

因此，对于在Training Data上得到不好的结果和在Training Data上得到好的结果但在Testing Data上得到不好的结果这两种情况，需要不同的解决方法。

Bad Results on Training Data

在不重新设计DNN结构时，如果在Training Data中得到Bad Results，一般有两种方法来改进结果：

• New activation function【neuron换新的激活函数】
• Adaptive Learning Rate

New activation function

Vanishing Gradient Problem

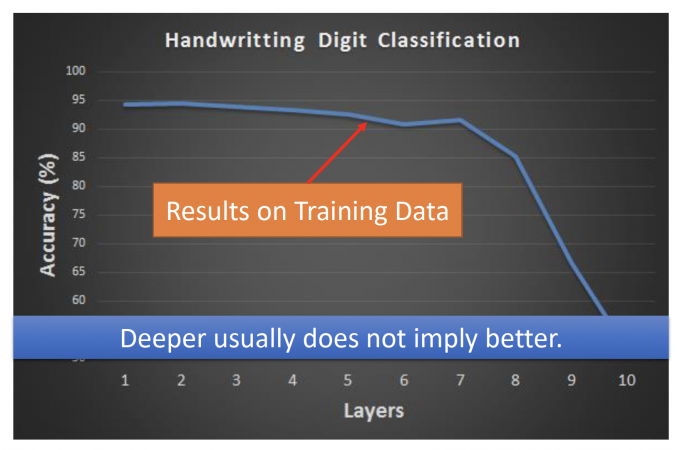
上图表示，在手写数字辨识中，Deeper layers并不能有好的performance。

为什么会这样呢？

因为出现了Vanishing Gradient Problem，即gradient随着deeper layer逐渐消失的问题。

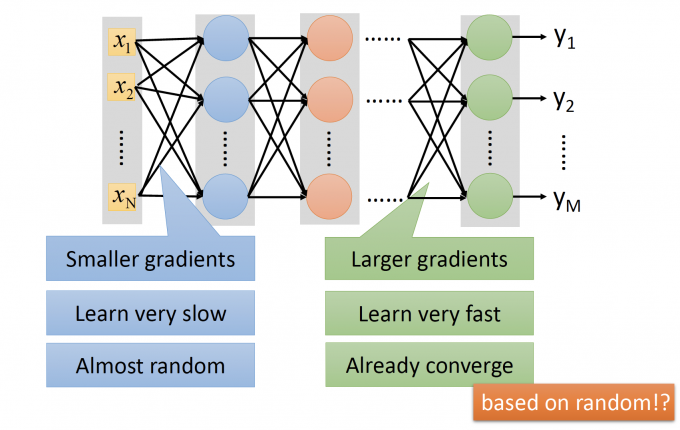
上图中，假设neuron的activation function是sigmod函数。

靠近Input layer层的参数的变化对Loss的影响很小，所以对Loss function做微分，gradient很小，参数更新慢。

而靠近Output layer层的参数的编号对Loss的影响更大，所以对Loss function做微分，gradient很大，参数更新快。

因为靠近Output Layer层的参数更新快，所以很快converge（收敛、趋于稳定）；但靠近Input Layer层的参数更新慢，几乎还处在random（随机）的状态。

当靠近Output Layer层的参数趋于稳定时，由于靠近Output Layer层的参数对Loss影响大，所以观察到的Loss的值也趋于稳定，于是，你就把training停掉了。

但是，靠近Input层的参数几乎处在random状态，所以拿模型用在Testing Data上，发现结果几乎是随机的。

---

怎么直观理解靠近Input Layer的参数的gradient小呢？

用微分的直观含义来表示gradient $\partial{l}/\partial{w}$ :

当 $w$ 增加 $\Delta{w}$ 时，如果 $l$ 的变化 $\Delta{l}$ 变化大，说明 $\partial{l}/\partial{w}$ 大，否则 $\partial{l}/\partial{w}$ 小。

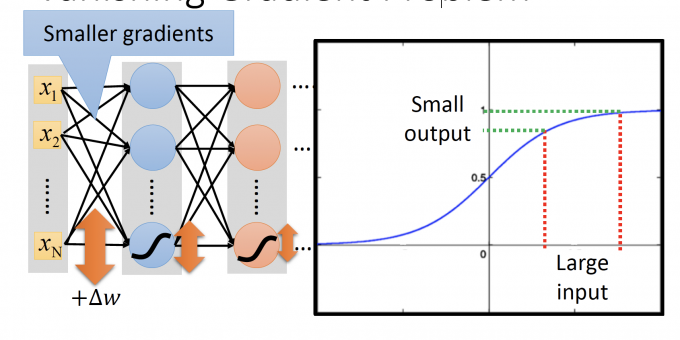
我们在DNN中使用的activation function是sigmod函数，sigmod函数会把值压到0和1之间。

因此，上图中，其他值不变，只有连接 $x_N$ 的参数 $w$ 增加 $\Delta w$ 时，输入通过neuron的sigmod函数，函数的输出增加的 $\Delta$ 会变小，随着Deeper Layer，neuron的输出的 $\Delta$ 会越变越小，趋至0。

最后DNN输出的变化对 loss的影响小，即 $\Delta{l}$ 趋至0，即参数的gradient $\partial{l}/\partial{w}$ 趋至0。（即 Vanishing Gradient）

ReLu ：Rectified Linear Unit

为了防止发生Vanishing Gradient Problem，在DNN中选择使用新的activation function。

ReLu长下面这个样子：

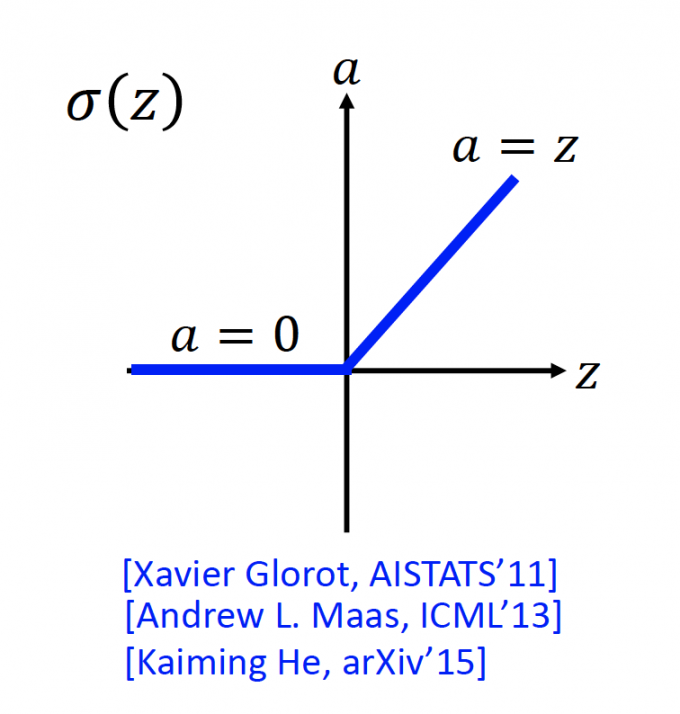
z: input

a: output

当 $z\leq0$ 时， $a=0$ ；当 $z >0$ 时， $a=z$ 。

Reason :

1. Fast to compute
2. Biological reason【有生物上的原因】
3. Infinite sigmod with different biases. 【是无穷个 有不同bias的sigmod函数 的叠加】
4. Vanishing gradient problem 【最重要的是没有vanishing gradient problem】

---

为什么ReLu没有vanishing gradient problem

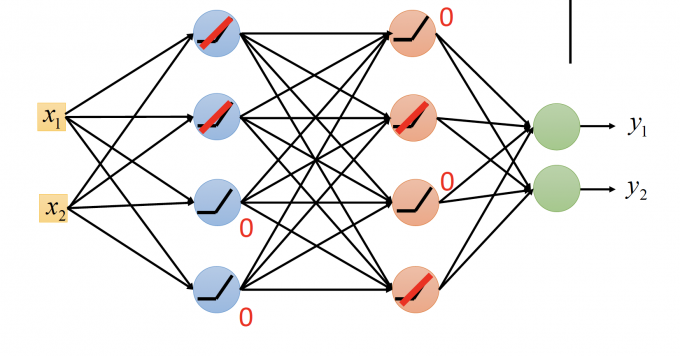
上图DNN中，ReLu在输入是负数时，输出是0。因此这些输出是0的neuron可以去掉。

就变成了下图这个A Thinner linear network。由于ReLu函数的性质，靠近Input Layer的参数不会有smaller gradient。

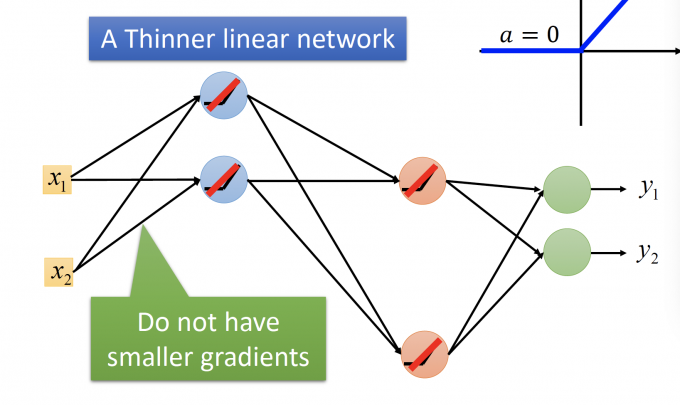
这里有一个Q&A:

Q1: function变成linear的，会不会DNN就变弱了？

： 当neuron的operation region不变的话，DNN的确是linear的，但是当neuron的operation region改变后，就是unlinear的。

：即，当input的变化小，operation region不变（即输入不会从大于0变成小于0，小于0变成大于0这种），model还是linear的；但当input的变化大时，很多neuron的operation region都变化了，model其实就是unlinear的。

Q2: ReLu 怎么微分？

：ReLu在0点不可微，那就随便指定为0这样（台湾腔QAQ）。

ReLu - variant

当 $z\leq 0$ 时，输出为0，就不能更新参数了。于是就有下图变体：

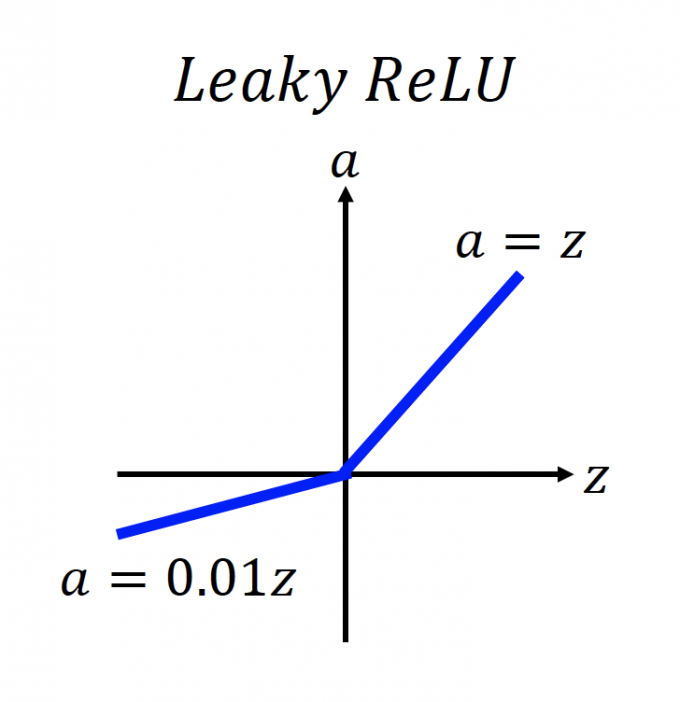
当 $z\leq0$ 时，gradient都为0.01，为什么不能是其他值。于是就有下图变体：其中 $\alpha$ 也是一个需要学习的参数

Maxout

Maxout，如下图，在设计neural network时，会给每一层的neuron分组，成为一个新的neuron。

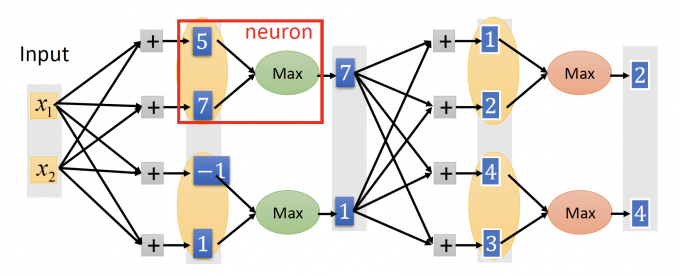
Maxout也是一个Learnable activation function。

ReLu是Maxout学出来的一个特例。

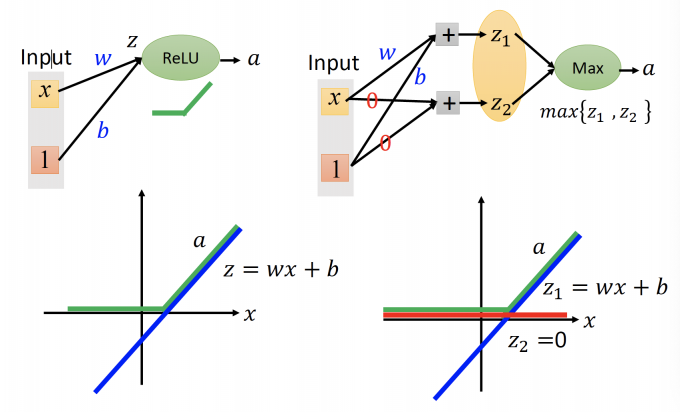
上图中，左图是ReLu。 ReLu的输入 $z = wx+b$ ，输出 $a$ 如上图的绿色的线。

右图是Maxout。Maxout的输入 $z_1 =wx+b,z_2=0$ ，那么输出取max，输出 $a$ 如上图中绿色的线，和左图的ReLu相同。

---

Maxout is more than ReLu。

当参数更新时，Maxout的函数图像如下图：

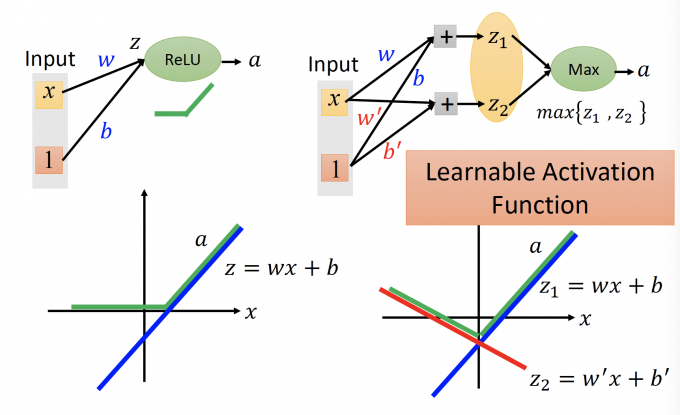
DNN中的参数是learnable的，所以Maxout也是一个learnable的activation function。

Reason ：

• Learnable activation function [Ian J. Goodfellow, ICML’13]

  • Activation function in maxout network can be any piecewise linear convex function.

    在maxout神经网络中的激活函数可以是任意的分段凸函数。

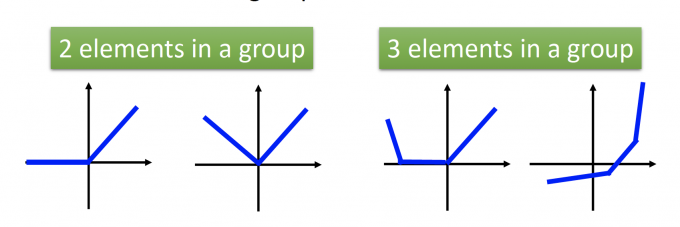
  • How many pieces depending on how many elements in a group.

    分段函数分几段取决于一组中有多少个元素。

    

Maxout : how to train

Given a training data x, we know which z would be the max.

【当给出每笔training data时，我们能知道Maxout neuron中哪一个最大】

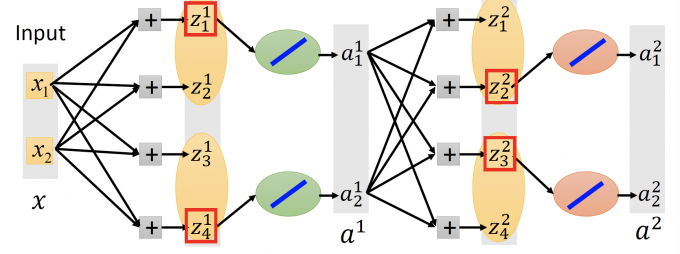
如上图，在这笔training data x中，我们只train this thin and linear network 的参数，即max z相连的参数。

每笔不同的training data x，会得到不同的thin and linear network，最后，会train到每一个参数。

Adaptive Learning Rate

Review Adagrad

在这篇文章： Gradient 第一小节讲到一种adaptive learning rate的gradient 算法：Adagrad 算法。在那篇文章中，我们得出的结论是 the best step $\propto$ |First dertivative| / Second derivative.

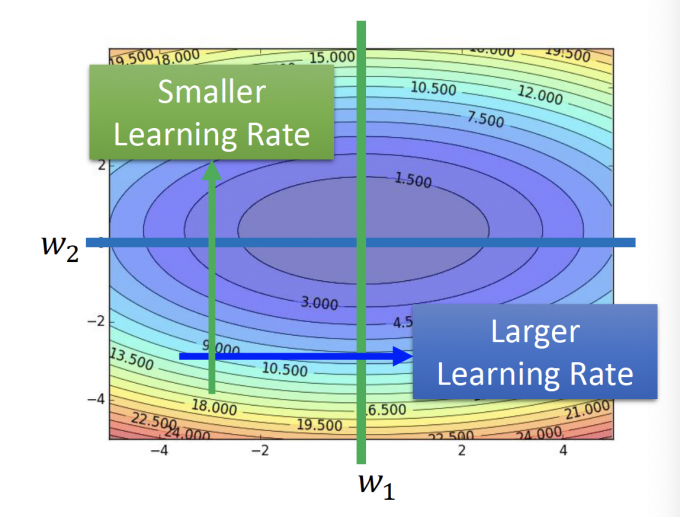
在上图中，两个方向，因为蓝色方向的二阶微分更小，所以蓝色方向应该有更大的learning rate。

因此，在Adagrad中，我们用一阶微分来估量二阶微分的大小：

$$ w^{t+1} \leftarrow w^{t}-\frac{\eta}{\sqrt{\sum_{i=0}^{t}\left(g^{i}\right)^{2}}} g^{t} $$

RMSProp

但是，在训练NN时，Error Surface（Total Loss对参数的变化）的图像可能会更复杂，如下图：

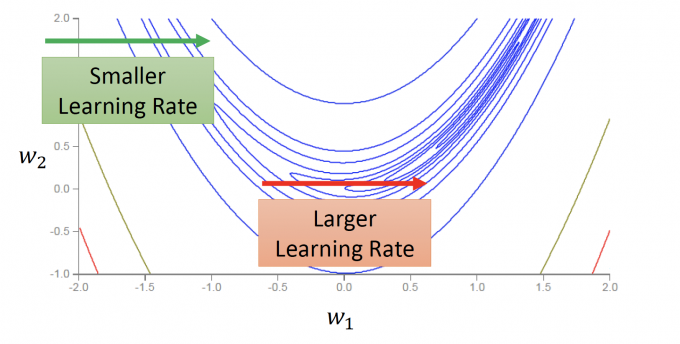
因为函数图像过于复杂，可能在同一方向的不同位置，也需要有不同的learning rate。

RMSProp是Adagrad的进阶版。

RMSProp过程：

1. $w^{1} \leftarrow w^{0}-\frac{\eta}{\sigma^{0}} g^{0} \quad \sigma^{0}=g^{0}$
2. $w^{2} \leftarrow w^{1}-\frac{\eta}{\sigma^{1}} g^{1} \quad \sigma^{1}=\sqrt{\alpha (\sigma^{0})^2+(1-\alpha)(g^1)^2}$
3. $w^{3} \leftarrow w^{2}-\frac{\eta}{\sigma^{2}} g^{2} \quad \sigma^{2}=\sqrt{\alpha (\sigma^{1})^2+(1-\alpha)(g^2)^2}$

4. …

5. $w^{t+1} \leftarrow w^{t}-\frac{\eta}{\sigma^{t}} g^{t} \quad \sigma^{t}=\sqrt{\alpha (\sigma^{t-1})^2+(1-\alpha)(g^t)^2}$

   $\sigma^t$ 也是在算gradients的 root mean squar。

但是在RMSProp中，加入了参数 $\alpha$ (需要手动调节大小的参数)，可以给当前算出来的gradient $g^t$ 更大的权重，即更相信现在gradient的方向，不那么相信以前gradient的方向。

Momentum

Momentum，则是引用物理中的惯性。

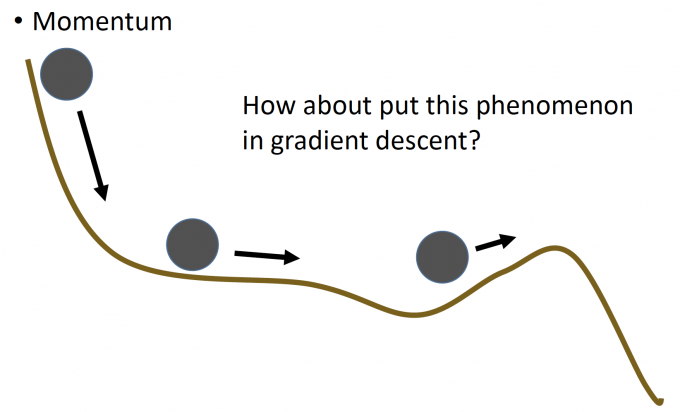
上图中，当小球到达local minima时，会因为惯性继续往前更新，则有可能到达minima的位置。

这里的Momentum，就代指上一次前进（参数更新）的方向。

Vanilla Gradient Descent

如果将Gradient的步骤画出图来，就是下图这样：

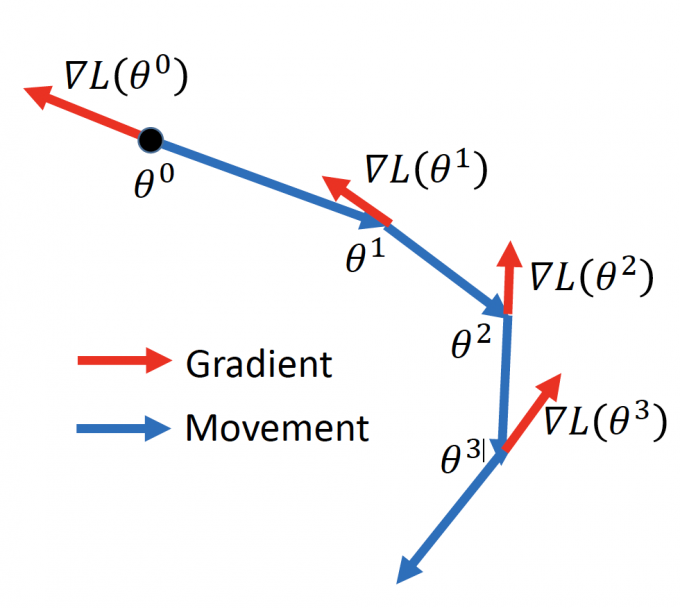
过程：

1. Start at position $\theta^0$

2. Compute gradietn at $\theta^0$

   Move to $\theta^1=\theta^0-\eta\nabla{L(\theta^0)}$

3. Compute gradietn at $\theta^1$

   Move to $\theta^2=\theta^1-\eta\nabla{L(\theta^1)}$

4. … …Stop until $\nabla{L(\theta^t)}\approx0$

---

Momentum

在Momentum中，参数更新方向是当前Gradient方向和Momentum方向（上一次更新方向）的叠加。

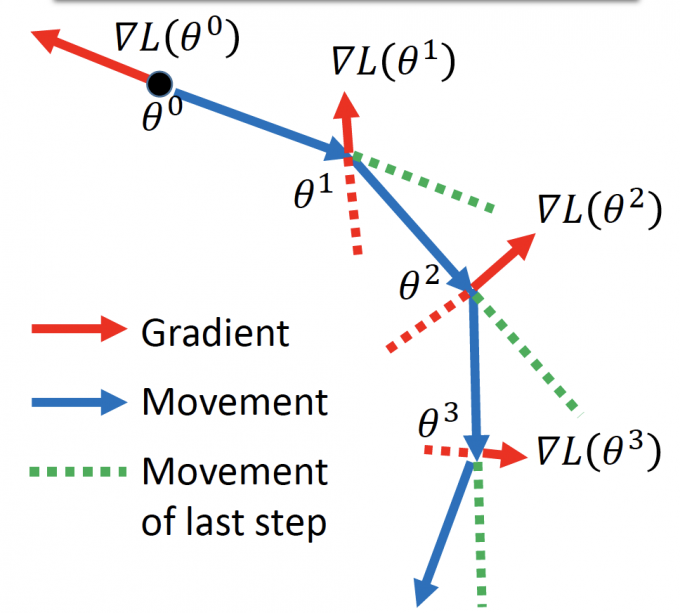
Movement方向：上一次更新方向 - 当前gradient方向。

过程：

1. Start at position $\theta^0$

   Movement: $v^0=0$

2. Compute gradient at $\theta^0$

   Movement $v^1=\lambda v^0-\eta\nabla{L(\theta^0)}$

   Move to $\theta^1=\theta^0+v^1$

3. Compute gradient at $\theta^1$

   Movement $v^2=\lambda v^1-\eta\nabla{L(\theta^1)}$

   Move to $\theta^2=\theta^1+v^2$

4. … …Stop until $\nabla{L(\theta^t)}\approx0$

和Vanilla Gradient Descent比较，$v^i$ 其实是过去gradient( $\nabla{L(\theta^0)}$ 、$\nabla{L(\theta^1)}$ 、… 、 $\nabla{L(\theta^{i-1})}$ )的加权和。

• 迭代过程：
  • $v^0=0$
  • $v^1=-\eta\nabla{L(\theta^0)}$
  • $v^2=-\lambda\eta\nabla{L(\theta^0)}-\eta\nabla{L(\theta^1)}$
  • …

---

再用那个小球的例子来直觉的解释Momentum：

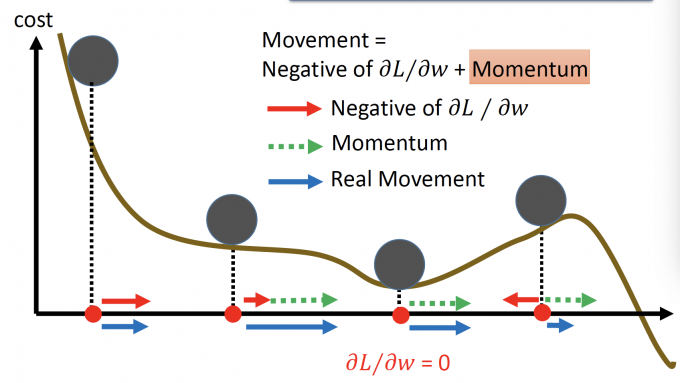
当小球在local minima时，gradient为0，但是Momentum（即上次移动方向）是继续往前，于是小球可以继续向前更新。

Adam = RMSProp + Momentum

Algorithm：Adam, our proposed algorithm for stochastic optimization.

【Adam，是为了优化stochastic gradient】（至于什么是stochastic gradient，建议戳Post not found: Gradietn 这篇)

$g_t^2$ indicates the elementwise square $g_t\odot g_t$ .

【$g_t^2$ 是gradient $g_t$ 向量和 $g_t$ 的元素乘】

Good default settings for the tested machine learning problems are $\alpha=0.001$ , $\beta_1=0.9$ , $\beta_2=0.999$ and $\epsilon=10^{-8}$ . All operations on vectors are element-wise. With $\beta_1^t$ and $\beta_2^t$ we denote $\beta_1$ and $\beta_2$ to the power t.

【参数说明：算法默认的参数设置是 $\alpha=0.001$ , $\beta_1=0.9$ , $\beta_2=0.999$ ， $\epsilon=10^{-8}$ 。算法中所有vector之间的操作都是对元素操作。 $\beta_1^t$ 和 $\beta_2^t$ 是 $\beta_1$ 和 $\beta_2$ 的 $t$ 次幂】

Adam Pseudo Code：

0. Require：$\alpha$ : Stepsize 【步长/learning rate $\eta$ 】

   Require：$\beta_1,\beta_2\in\left[0,1\right)$ : Exponential decay rates for the moment estimates.

   Require：$f(\theta)$ : Stochastic objective function with parameters $\theta$ .【参数 $\theta$ 的损失函数】

   Require: $\theta_0$ ：Initial parameter vector 【初值】

1. $m_0\longleftarrow 0$ (Initial 1st moment vector) 【 $m$ 是Momentum算法中的更新参数后的方向 $v$ 】

   $v_0\longleftarrow 0$ (Initial 2nd moment vector) 【 $v$ 是RMSprop算法中gradient的root mean square $\sigma$ 】

   $t\longleftarrow 0$ (Initial timestep) 【更新次数】

2. while $\theta_t$ not concerged do 【当 $\theta$ 趋于稳定，即 $\nabla{f(\theta)}\approx0$ 时】

   1. $t\longleftarrow t+1$

   2. $g_t\longleftarrow \nabla{f_t(\theta_{t-1})}$ (Get gradients w.r.t. stochastic objective at timestep t)

      【算第t次时 $\theta$ 的gradient】

   3. $m_{t} \leftarrow \beta_{1} \cdot m_{t-1}+\left(1-\beta_{1}\right) \cdot g_{t}$ (Update biased first momen t estimate)

      【用Momentum算更新方向】

   4. $v_{t} \leftarrow \beta_{2} \cdot v_{t-1}+\left(1-\beta_{2}\right) \cdot g_{t}^{2}$ (Update biased second raw moment estimate)

      【RMSprop估测最佳步长（ 和$v$ 负相关） 】

   5. $\widehat{m}_{t} \leftarrow m_{t} /\left(1-\beta_{1}^{t}\right)$ （Comppute bbi. as-corrected first momen t estima te)

      【算出来的值有bias，论文中有具体解释为什么有。当更新次数增加时， $1-\beta_1^t$ 也趋近于1】

   6. $\widehat{v}_{t} \leftarrow v_{t} /\left(1-\beta_{2}^{t}\right)$ (Compute bias-corrected second raw momen t estimate)

      【和上同理】

   7. $\theta_{t} \leftarrow \theta_{t-1}-\alpha \cdot \widehat{m}_{t} /(\sqrt{\widehat{v}_{t}}+\epsilon)$ （Update parameters）

      【 $\widehat{m}t$ 相当于是更准确的gradient的方向，$\sqrt{\widehat{v}{t}}+\epsilon$ 是为了估测最好的步长，调节learning rate】

Gradient Descent Limitation？

在Gradient这篇文章中，讲到过Gradient有一些问题不能处理：

• Stuck at local minima
• Stuck at saddle point
• Very slow at the plateau

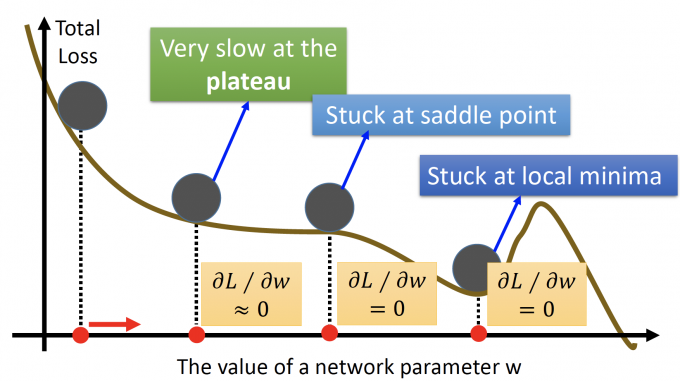
（李老师说的，不是我说的QAQ）：但是Andrew（吴恩达）在2017年说过，不用太担心这个问题。为什么呢？

如果要stuck at local minima，前提是每一维度都是local minima。

如果在一个维度遇到local minima的概率是p，当NN很复杂时，有很多参数时，比如1000，那么遇到local minima的概率是 $p^{1000}$ ，趋近于0了，几乎不会发生。

：所以不用太担心Gradient Descent的局限性。

Bad Results on Testing Data

Early Stopping

在更新参数时，可能会出现这样曲线图：

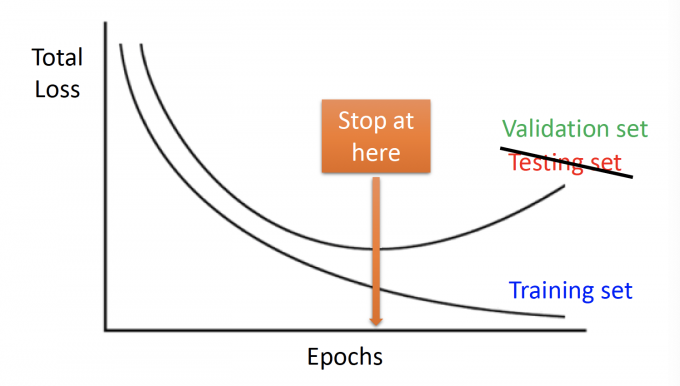
图中，Total Loss在training set中逐渐减小，但在validation set中逐渐增大。

而我们真正关心的其实是validation set的Loss。

所以想让参数停在validation set中loss最低时。

Keras能够实现EarlyStopping功能[1]：click here

from keras.callbacks import EarlyStopping
early_stopping = EarlyStopping(monitor='val_loss', patience=2)
model.fit(x, y, validation_split=0.2, callbacks=[early_stopping])

Regularization

Regularization：Find a set of weight not only minimizing original cost but also close to zero.

构造一个新的loss function，除了最小化原来的loss function，还能使得参数趋紧0，使得function更平滑。

function的曲线更平滑，当输入有轻微扰动，不会太影响输出的结果。

L2 norm regularization

New loss function:

$$ \begin{equation} \begin{aligned} \mathrm{L}^{\prime}(\theta)&=L(\theta)+\lambda \frac{1}{2}\|\theta\|_{2} \\ \theta &={w_1,w_2,...} \\ \|\theta\|_2&=(w1)^2+(w_2)^2+... \end{aligned} \end{equation} $$

其中用第二范式 $\lambda\frac{1}{2}|\theta|_2$ 作为regularization term。做regularization是为了使函数更平滑，所以一般不考虑bias)

New gradient:

$$ \frac{\partial \mathrm{L}^{\prime}}{\partial w}=\frac{\partial \mathrm{L}}{\partial w}+\lambda w $$

New update:

$$ \begin{equation} \begin{aligned} w^{t+1} &\longrightarrow w^{t}-\eta \frac{\partial \mathrm{L}^{\prime}}{\partial w} \\ &=w^{t}-\eta\left(\frac{\partial \mathrm{L}}{\partial w}+\lambda w^{t}\right) \\ &=(1-\eta \lambda) w^{t}-\eta \frac{\partial \mathrm{L}}{\partial w} \end{aligned} \end{equation} $$

在更新参数时，先乘一个 $(1-\eta\lambda)$ ，再更新。

weight decay（权值衰减）：由于 $\eta,\lambda$ 都是很小的值，所以 $w^t$ 每次都会先乘一个小于1的数，即逐渐趋于0，实现regularization。但是，因为更新中还有gradient部分，所以不会等于0。

L1 norm regularization

Regularization除了用第二范式，还可以用其他的，比如第一范式 $|\theta|_1=|w_1|+|w_2|+…$

New loss function:

$$ \begin{equation}\begin{aligned}\mathrm{L}^{\prime}(\theta)&=L(\theta)+\lambda \frac{1}{2}\|\theta\|_1\\ \theta &={w_1,w_2,...} \\ \|\theta\|_1&=|w_1|+|w_2|+...\end{aligned}\end{equation} $$

用sgn()符号函数来表示绝对值的求导。

符号函数：Sgn(number)

如果number 大于0，返回1；等于0，返回0；小于0，返回-1。

New gradient:

$$ \frac{\partial \mathrm{L}^{\prime}}{\partial w}=\frac{\partial \mathrm{L}}{\partial w}+\lambda \text{sgn}(w) $$

New update:

$$ \begin{equation} \begin{aligned} w^{t+1} &\longrightarrow w^{t}-\eta \frac{\partial \mathrm{L}^{\prime}}{\partial w} \\ &=w^{t}-\eta\left(\frac{\partial \mathrm{L}}{\partial w}+\lambda \text{sgn}(w^t)\right) \\ &=w^{t}-\eta \frac{\partial \mathrm{L}}{\partial w}-\eta \lambda \operatorname{sgn}\left(w^{t}\right) \end{aligned} \end{equation} $$

在用第一范式做regularization时，每次 $w^t$ 都要减一个值 $\eta\lambda\text{sgn}(w^t)$ ，和用第二范式做regularization比较，后者每次都要乘一个小于1的值，即使是乘0.99，w下降也很快。

Weight decay（权值衰减）的生物意义：

Our brain prunes（修剪） out the useless link between neurons.

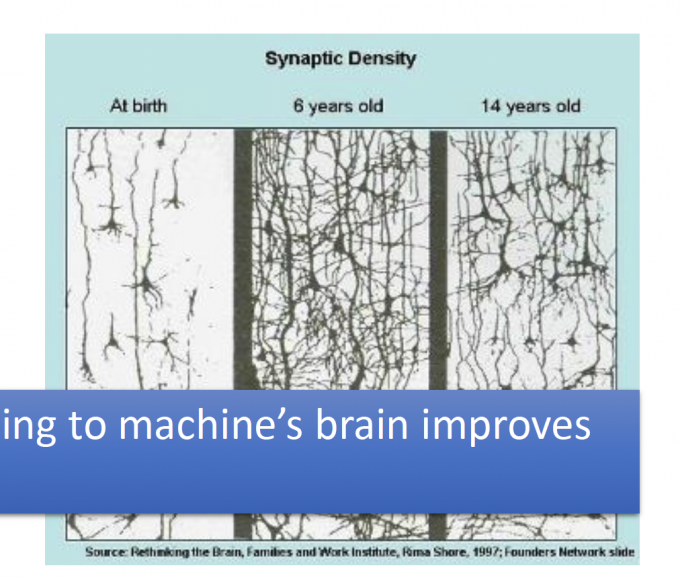
Dropout

Wiki: Dropout是Google提出的一种正则化技术，用以在人工神经网络中对抗过拟合。Dropout有效的原因，是它能够避免在训练数据上产生复杂的相互适应。Dropout这个术语代指在神经网络中丢弃部分神经元（包括隐藏神经元和可见神经元）。在训练阶段，dropout使得每次只有部分网络结构得到更新，因而是一种高效的神经网络模型平均化的方法。[2]

这里讲Dropout怎么做。

Training

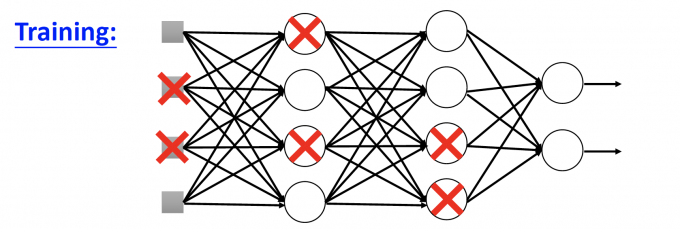
• Each time before updating the parameters:

  • Each neuron has p% to dropout. Using the new thin network for training.

    【如上图，每个neuron有p的概率被dropout。于是NN就变成了下图thinner的NN】

    

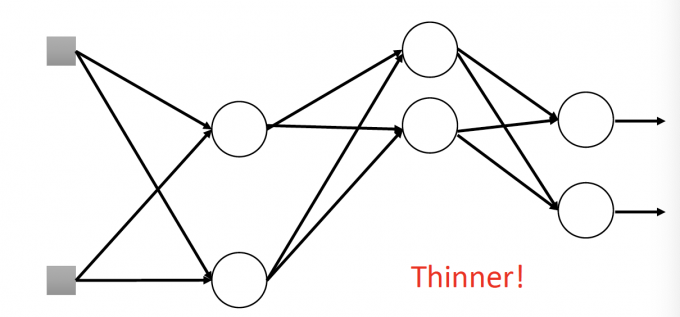
  • For each mini-batch, we resample the dropout neurons.

    【每次mini-batch，都要重新dropout，更新NN的结构】

Testing

Testing中不做dropout

• If the dropout rate at training is p%, all the weights times 1-p%.

  【如果在training中 dropout rate是 p%，在testing是，每个参数都乘 （1-p%)】

  【比如dropout rate 是0.5。如果train出来的w是 1，那么testing中 w=0.5】

Why dropout in training：Intuitive Reason

1. 这是一个比较有趣的比喻：

   

2. 这也是一个有趣的比喻hhh:

   

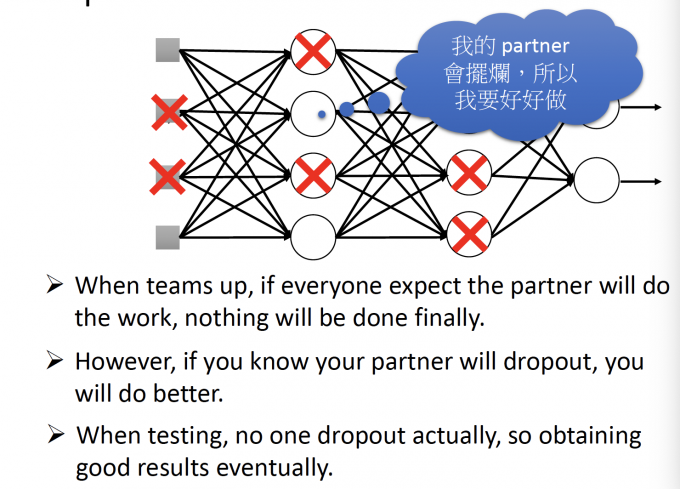
   即，团队合作的时候，如果每个人都认为队友在带我，那每个人都可能划水。

   但是，（training中）如果你知道你的队友在划水，那你可能会做的更好。

   但是，（testing中）发现每个人都有更好地做，都没有划水，那么结果就会很好。

   （hhhh，李老师每次讲Intuitive Reason的时候，都觉得好有道理hhh，科学的直觉orz给我也整一个）

Why multiply (1-p%) in testing: Intuitive reason

为什么在testing中 weights要乘（1-p%)?

用一个具体的例子来直观说明：

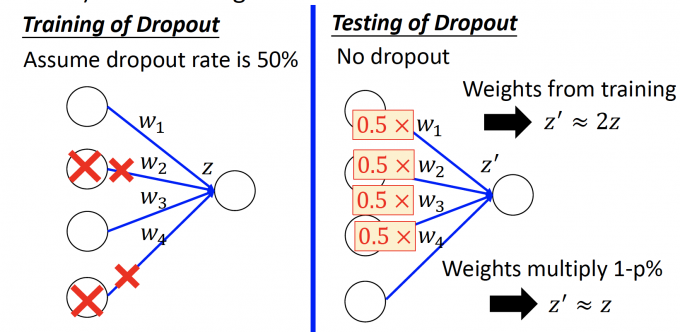
上图中，如果dropout rate=0.5，假设只训练一次， $w_2,w_4$ 相连的neuron都被dropout。

在testing中，因为不对neurondropout，所以如果不改变weight，计算出的结果 $z’\approx 2z$ 。

因此将所有weight简单地和(1-p%) 相乘，能尽量保证计算出的结果 $z’\approx z$ 。

Dropout is a kind of ensemble

Ensemble(合奏)，如下图，将testing data丢给train好的NN来估计，最后的估计值取所有NN输出的平均，如下图：

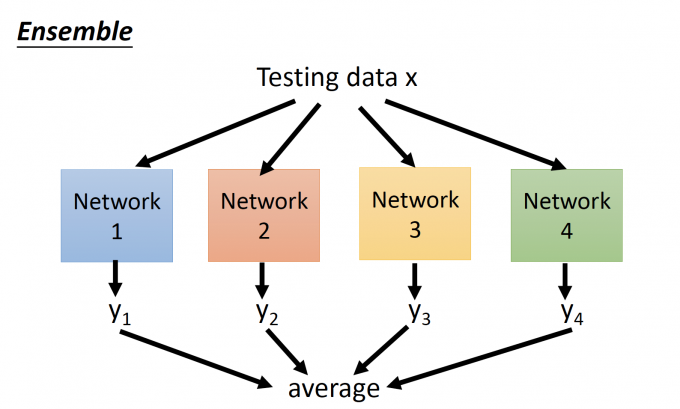
为什么说dropout is a kind of ensemble?

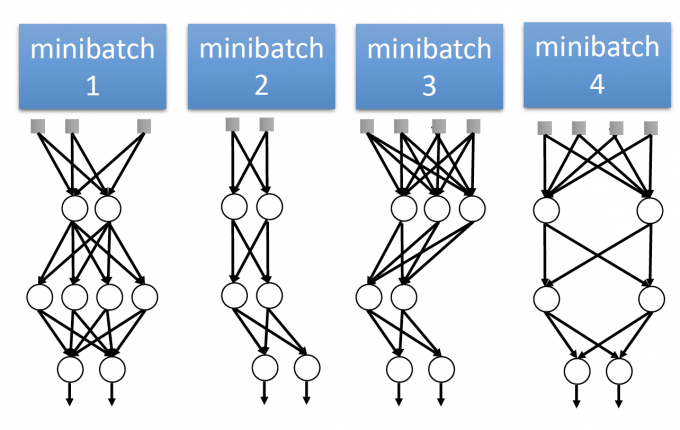
• Using one mini-batch to train one network

  【dropout相当于每次用一个mini-batch来训练一个network】

• Some parameters in the network are shared

  【有些参数可能会在很多个mini-batch都被train到】

由于每个神经元有 p%的概率被dropout，因此理论上，如果有M个neuron，可能会训练 $2^M$ 个network。

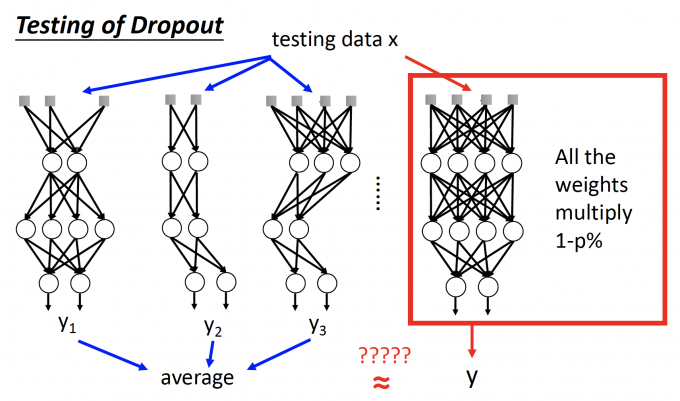
但是在Ensemble中，将每个network存下来，testing的时候输出取平均，这样的过程太复杂了，结果也不一定会很好。

所以在testing中，no dropout，对原始network中的每个参数乘 (1-p%)，用这样简单的操作来达到ensemble的目的。

Reference

1. Keras: how can i interrupt training when the validation loss isn’t decresing anymore.
2. Dropout-wiki：https://zh.wikipedia.org/wiki/Dropout