「机器学习-李宏毅」:Convolution Neural Network(CNN)
这篇文章中首先介绍了为什么要用CNN做图像识别,或者说图像识别问题的特点是什么?
文章中也详细介绍了CNN的具体架构,主要包括Convolution、Max Pooling、Flatten。
文章最后简要介绍了CNN在诸多领域的应用。
Why CNN for Image?
图片本质都是pixels。
在做图像识别时,本质是对图片中的某些特征像素(properities)识别。
So Why CNN for image?
Some patterns are much smaller than the whole image.
A neuron does not have to see the whole image to discover the pattern.
Connecting to small region with less parameters.
【很多特征图案的大小远小于整张图片的大小,因此一个neuron不需要为了识别某个pattern而看完整张图片。并且,如果只识别某个小的region,会减少大量参数的数目。】
如下图,用一个neuron识别红框中的beak,即能大概率认为图片中有bird。
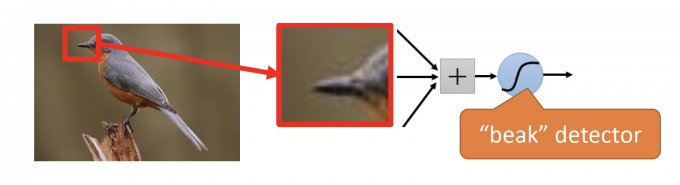
The same patterns appear in different regions. They can use the same set of parameters.
【同样的pattern可能出现在图片的不同位置。pattern几乎相同,因此可以用同一组参数。】
如下图,两个neuron识别两个不同位置的beak。被识别的beak几乎无差别,因此neuron的参数可以是相同的。
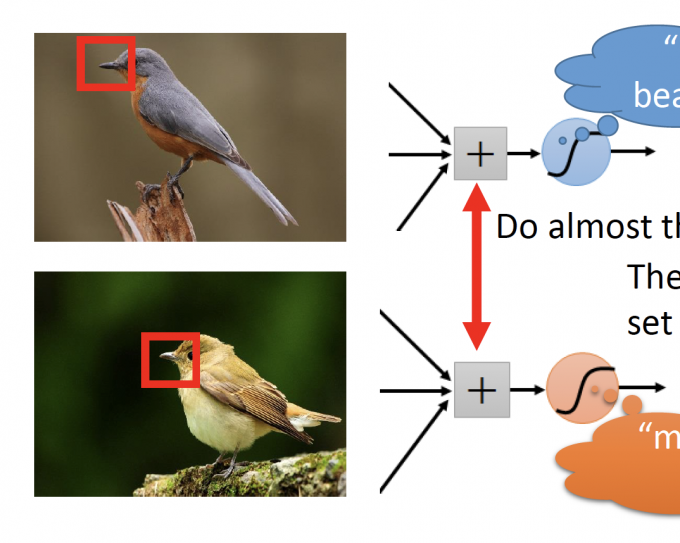
Subsampling the pixels will not change the object.
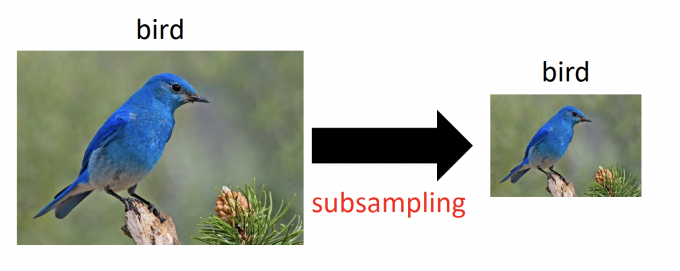
【一张图片是由许多pixel组成的,如下图,如果去掉图片的所有奇数行偶数列的pixel,图片内容几乎无差别。并且,Subsample pixels,即减少了输入的size,也可以减少NN的参数数量。】
The whole CNN
CNN的架构如下图。
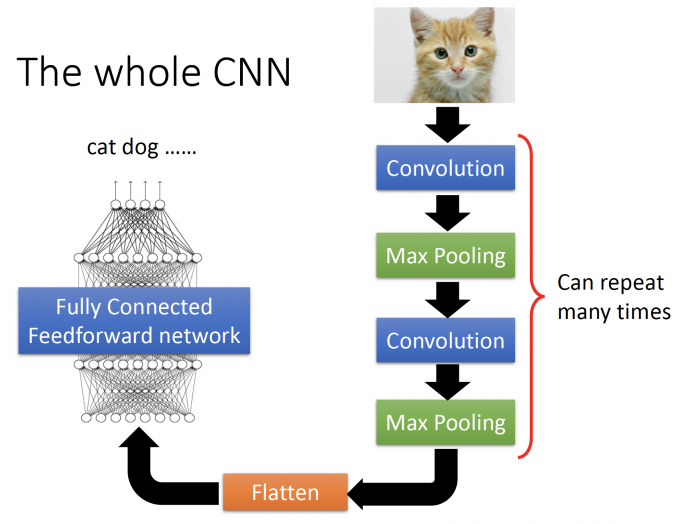
一张图片经过多次Convolution、Max Pooling得到新的image,再将新的image Flatten(拉直)得到一组提取好的features,将这组features放入前馈神经网络。
Convolution满足图片识别的:
- Property 1 : Some patterns are much smaller than the whole image.
- Property 2 : The same patterns appear in different regions.
Max Pooling满足图片识别的:
- Property 3 : Subsamplingthe pixels will not change the object.
CNN-Convolution
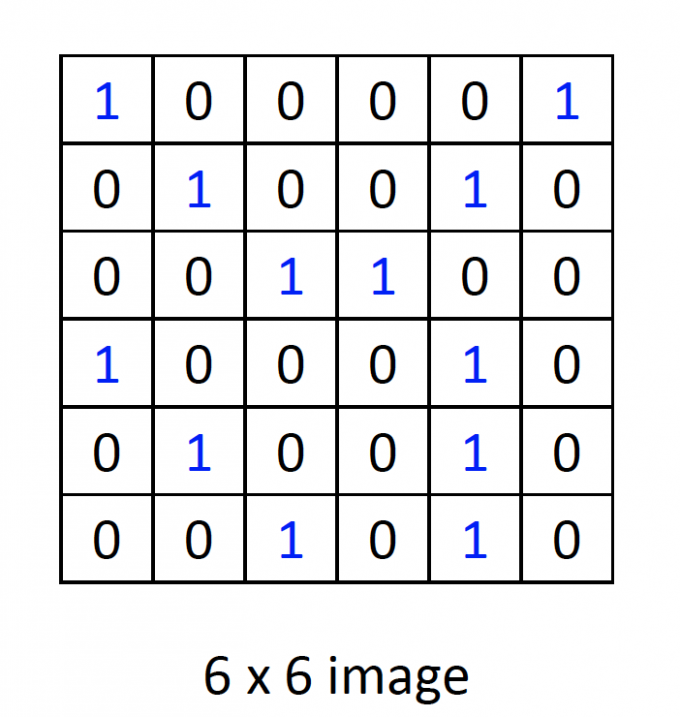
一张简单的黑白图片如下图,0为白色,1为黑色。
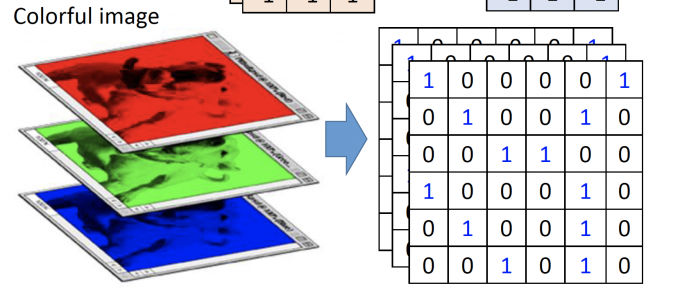
如果图片是彩色的,即用RGB三原色来表示,用三个matrix分别表示R、G、B的值,如下图:
下文中,以黑白图举例。
Property 1
设计Filer matrix满足Property 1,如下图:
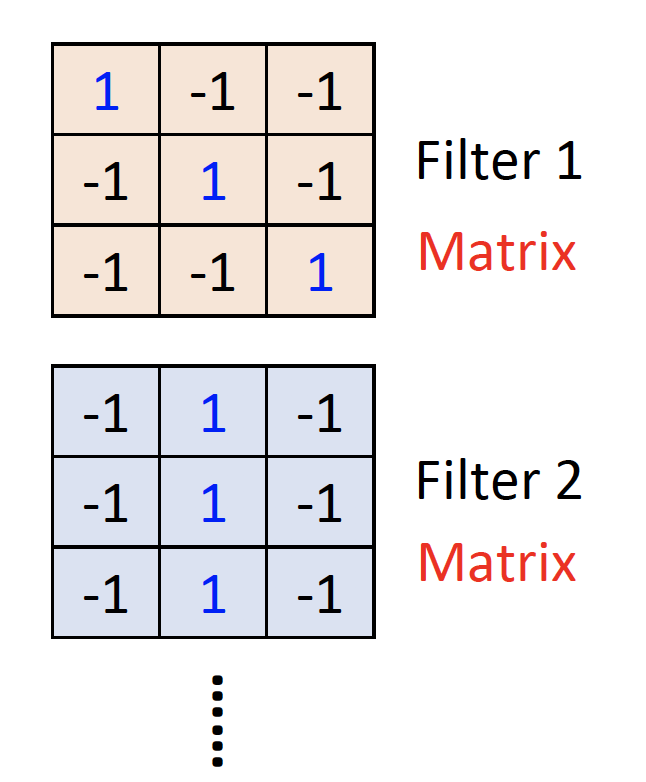
上图中,filter的大小是3*3,可以检测到小区域的某个pattern。
每个filter的参数都是NN中的参数,需要learned。
如果是彩色图片,filter应该是3张3*3matrix组成的,分别代表R、G、B的filter。
Property 2
为了满足Property 2,filter可以在图片中移动。设置stride,即每次filter移动的步长。
filter与覆盖图片的位置做内积,需要走完整张图片,最后得到一张feature map。
下图为stride=1的convolution结果:
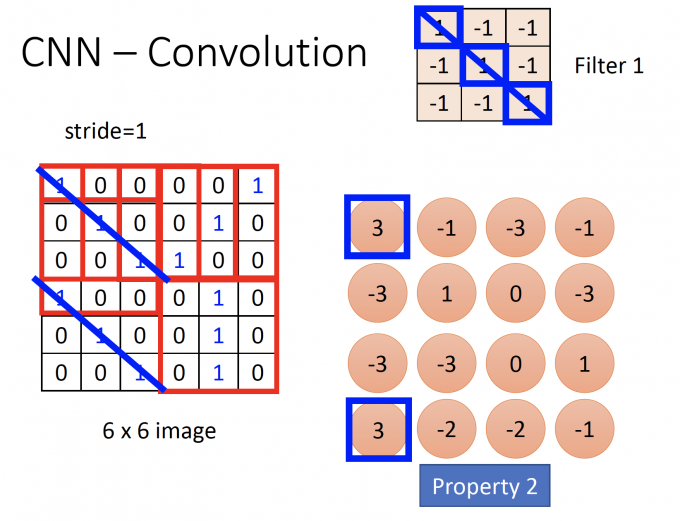
Convolution layer(卷积层)有几个filter,就会得到几张feature maps。
Convolution v.s. Fully Connected
Fully Connected:
如果用全连接的方式做图片识别,图片的每一个pixel都要和第一层的所有neurons连接,需要大量参数。
如下图:
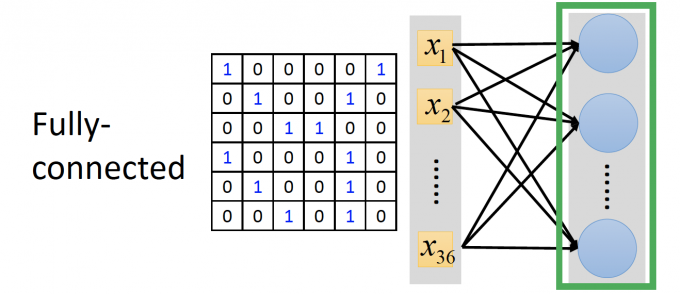
Convolution:
而在Convolution中,把feature map中的每一个值作为neuron的输出,因此图片中只有部分pixels会和第一层的第一个neuron连接,而不是全部pixels。
对于一个3*3的filter,一个neuron的连接如下:
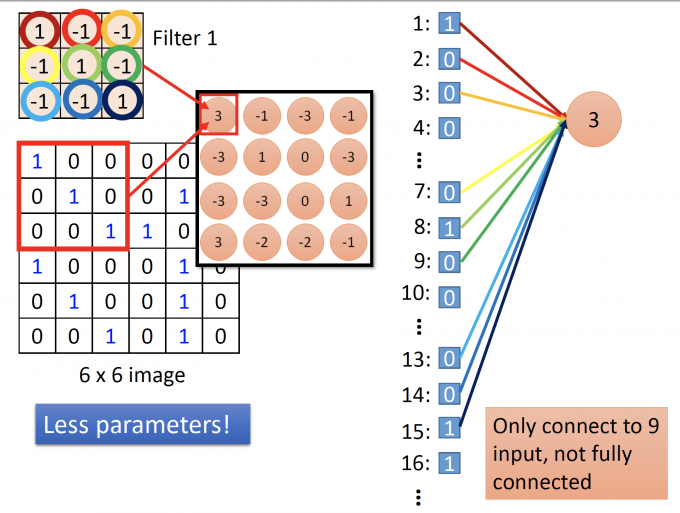
filter中的值是连接参数,则每一个neuron只需要与3*3个input连接,与全连接相比减少了大量参数。
shared weights
filter在图中移动时,filter的参数不变,即第二个neuron的连接参数和第一个neuron的连接参数是相同的,连接图如下:
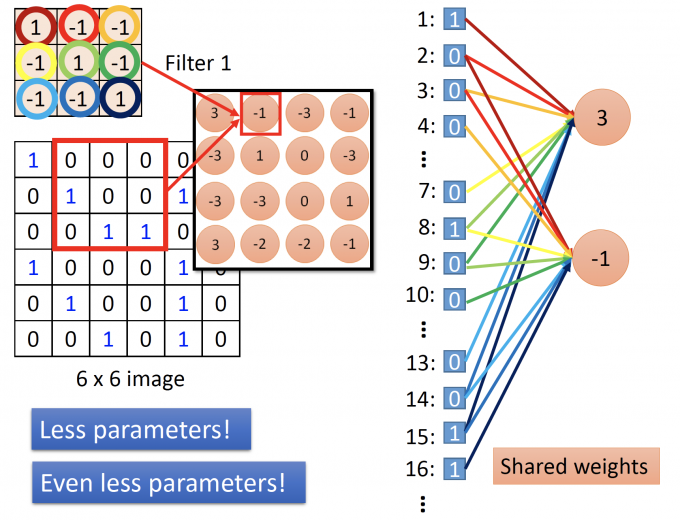
通过filter实现了shared weights(参数共享),更大幅度减少了参数数量。
CNN-Max Pooling
Max Pooling:将convolution layer的neuron作为输入,neuron的activation function其实就是Maxout(Maxout介绍见 Post not found: tips-for-DL/#Maxout 这篇 的介绍)。
将convolution layer得到的feature map做Max pooling(池化),即取下图中每个框中的最大值。
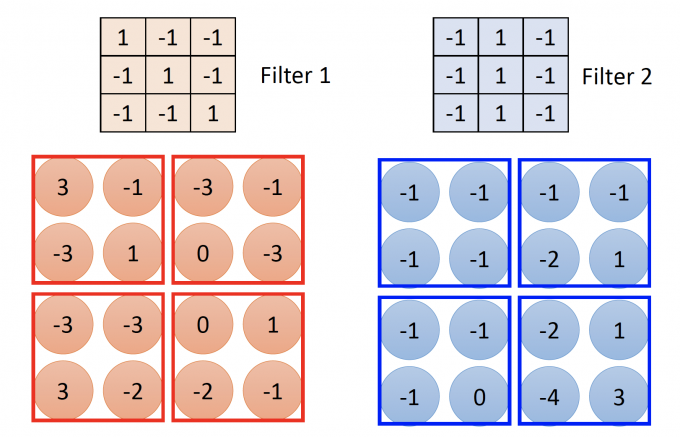
如下图,6*6的image经过Convolution layer 和 Max Pooling layer后,得到了new but smaller image,新的image的由两层channel组成,每层channel都是2 * 2的image。
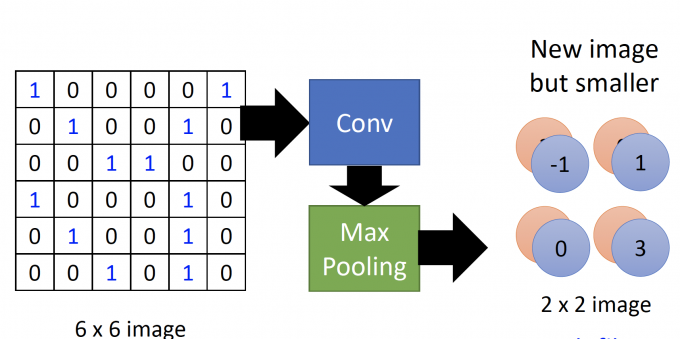
一个image每经过一次Convolution layer 和 Max Pooling layer,都会得到a new image。
This new image is smaller than the origin image. And the number of channel (of the new image) is the number of filters.
举个例子:
Convolution layer有25个filters,再经过Max Pooling,得到的新的image有25 个channel。
再重复一次Convolution 和Max Pooling,新的Convolution layer也有25个filters,再经过Max Pooling,得到的新的image有多少个channel呢?
答案是25个channel。
注意 :在第二次Convolution中,image有depth,depth=25。因此在convolution中,filter其实是一个cubic,也有depth,depth=image-depth=25,再做内积。
因此,新的image的channel数是等于filter数的。
Flatten
Flatten很好理解,将最后得到的新的image 拉直(Flatten)为一个vector。
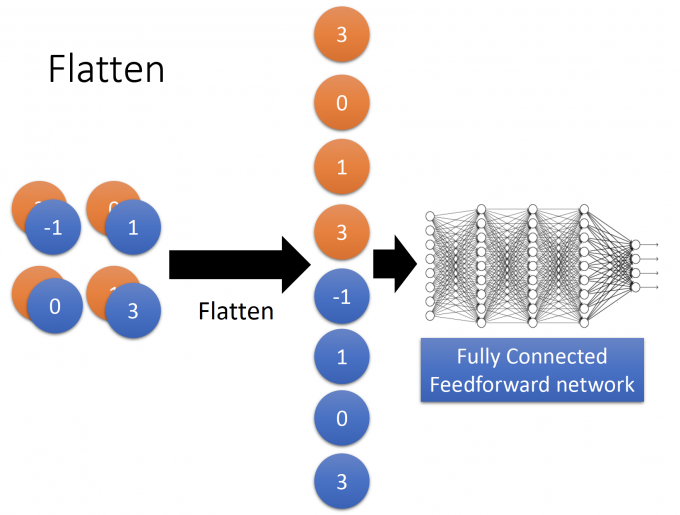
拉直后的vector是一组提取好的features,作为 前馈神经网络的输入。
zero padding
如何让卷积后的图像不变小?
答案就是zero padding,在原图的padding填0,再做卷积。
zero-padding后如下图:
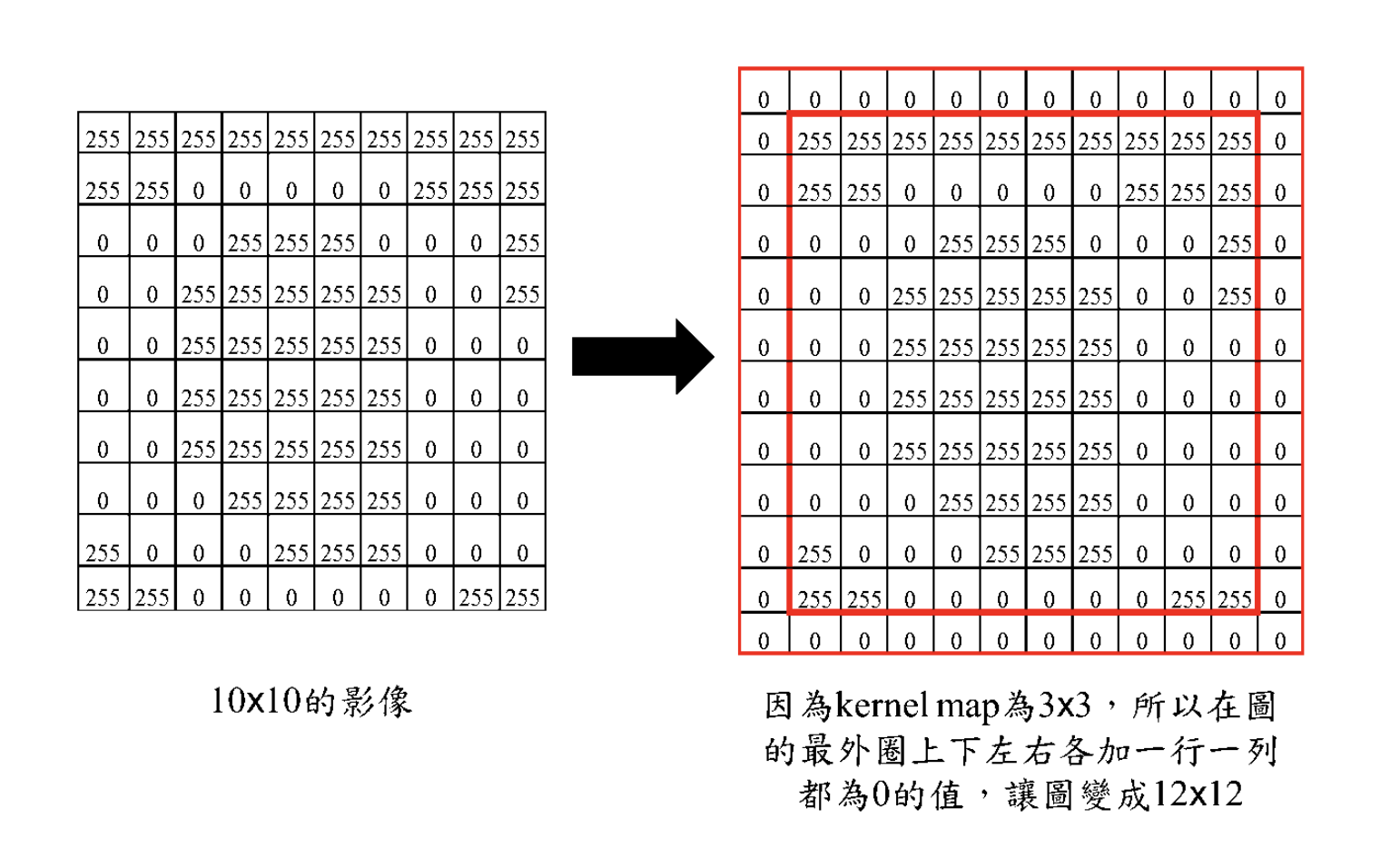
卷积后,图像大小不变:
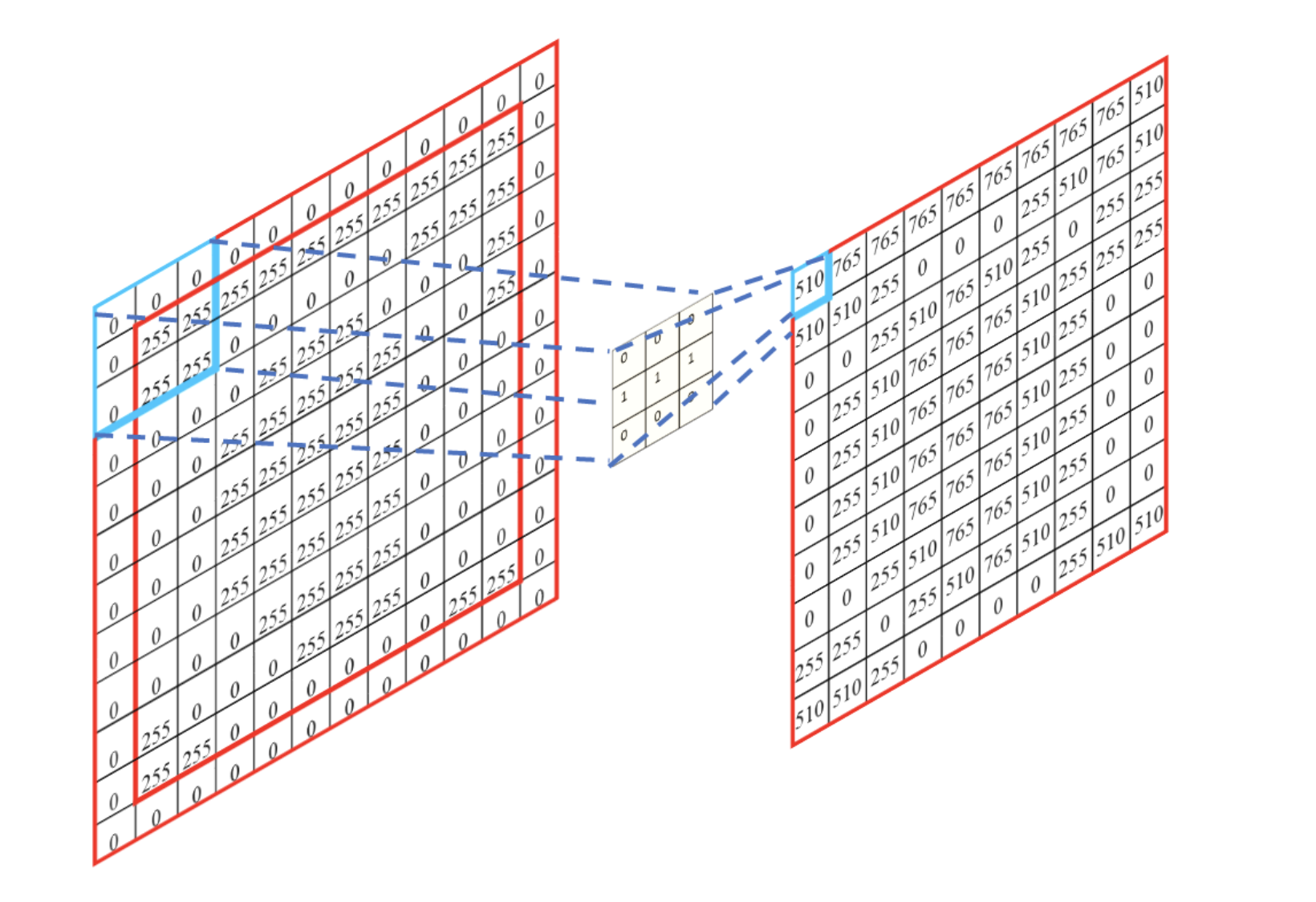
What dose CNN learn
为什么CNN能够学习pattern,最终达到识别图像的目的?
Filter
在下图CNN过程中,我们先分析能从Convolution layer的filter能够学到什么?
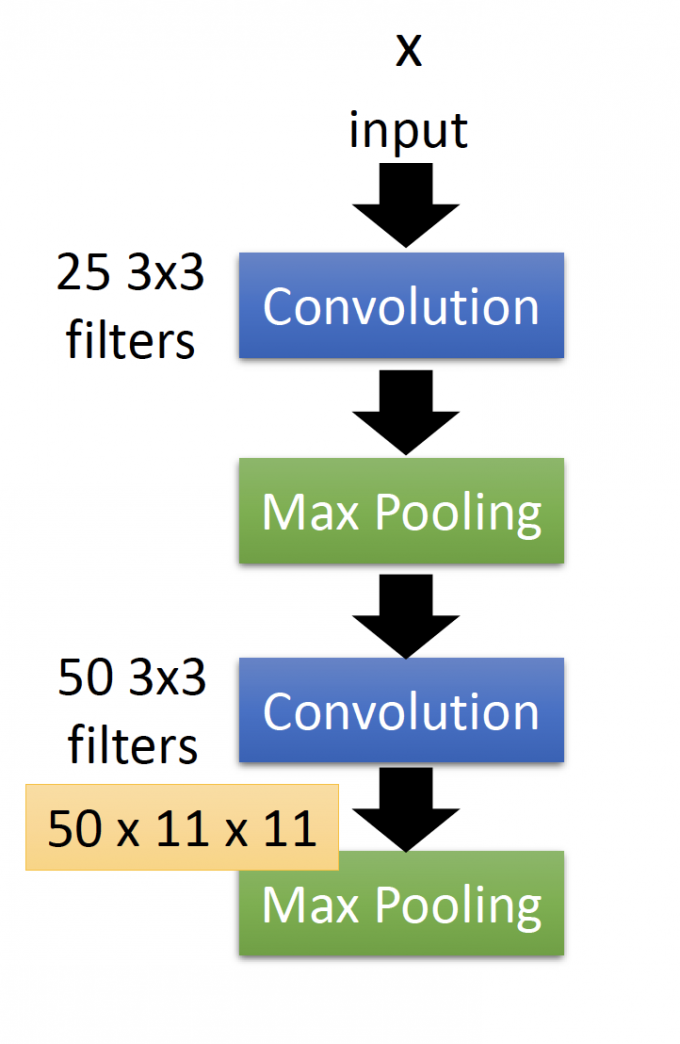
每个filter本质上是一组shared weights 的neuron。
因此,定义这组filter的激活程度,即:
Degree of the activation of the k-th filter: $a^k=\sum_{i=1}^{11}\sum_{j=1}^{11}a_{ij}^{k}$ .
目标是找到使k-th filter激活程度最大的输入image,即
$x^{*}=\arg \max _{x} a^{k}$ ,(method :gradient descent).
部分结果如下图:

(每一张图都代表一个让filter激活程度最大的 $x$)
上图中,找到使filter激活程度最大的image,即上图中每个filter可以检测一定的条纹,只有当图像中有该条纹,filter(一组neuron)的激活程度(即输出)才能达到最大。
Neuron(Hidden layer)
这里的neuron指前馈神经网络中的neuron,如下图的 $a_j$ :
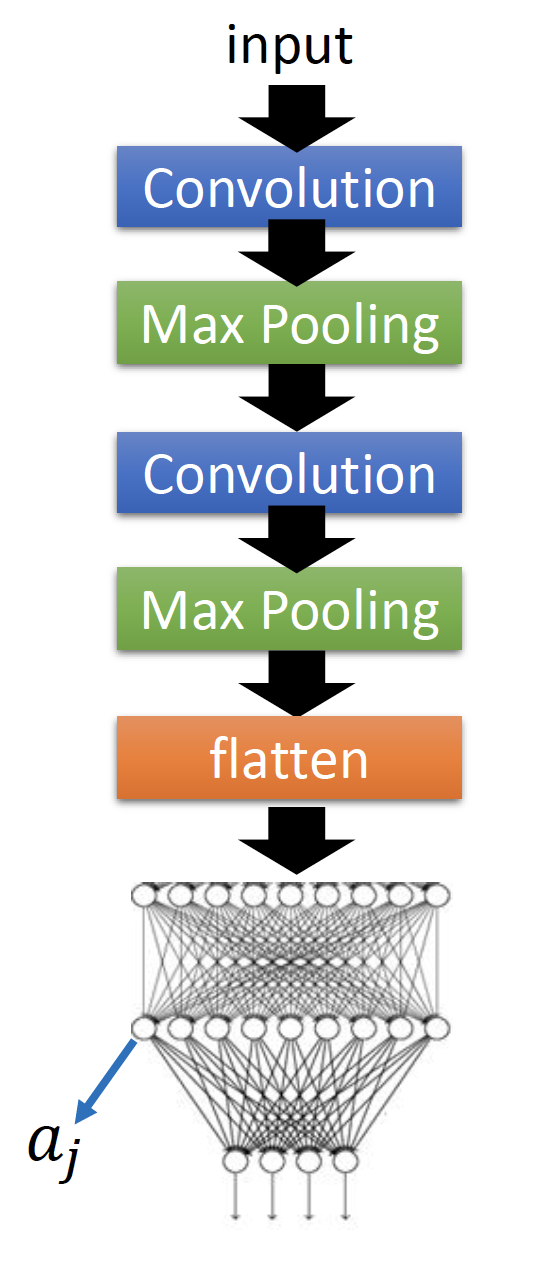
目标:找到使neuron的输出最大的输入image,即:
$x^{*}=\arg \max _{x} a^{j}$ .
部分结果如下:

(每一张图代表一个neuron)
在上图中,感觉输入像一个什么东西吧emmmm。
但和filter学到的相比,neuron学到的不仅是图中的小小的pattern(比如条纹、鸟喙等),neuron学的是看整张图像什么。
Output(Output layer)
再用同样的方法,看看输出层的neuron学到了什么,如下图的 $y_i$ :
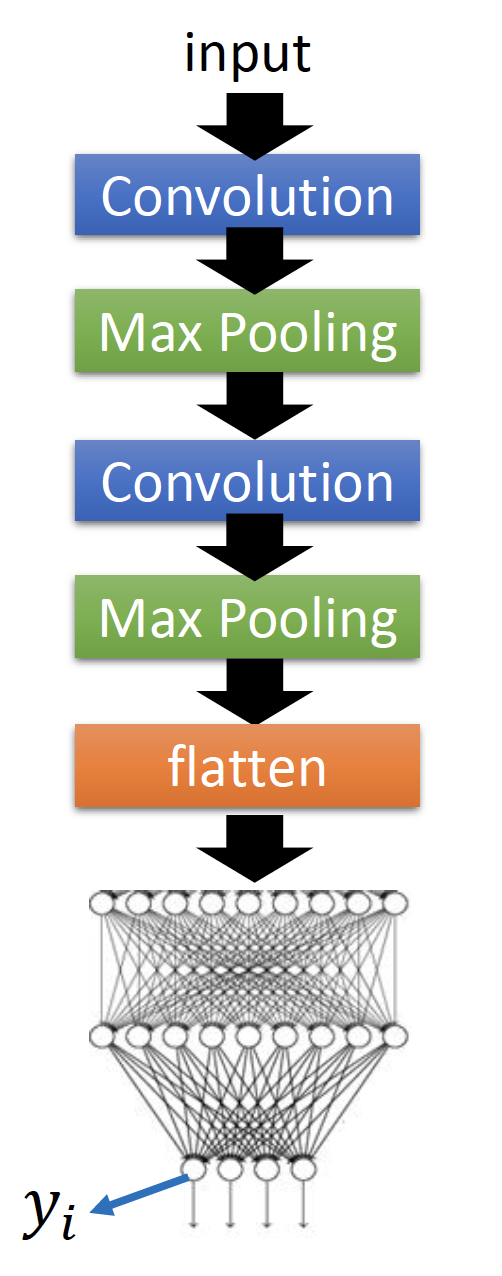
在手写数字辨识中 $y_i$ 是数字为 $i$ 的概率,因此目标是:找到一个使输出是数字 $i$ 概率最大的输入image,即:
$x^{*}=\arg \max _{x} y^{i}$ .
结果如下图:

结果和我们期望相差甚远,根本不能辨别以上图片是某个数字。
这其实也是DNN的一个特点: Deep Neural Networks are Easily Fooled [1],即NN学到的东西往往和人类学到的东西是不一样的。
CNN
所以CNN到底学到了什么?
上文中,output 学到的都是一团密密麻麻杂乱的像素点,根本不像数字。
但是,再考虑手写数字image的特点:图片中应该有少量模式,大片空白部分。
因此目标改进为: $x^{*}=\arg \max _{x}\left(y^{i}+\sum_{i, j}\left|x_{i j}\right|\right)$
$\sum_{i, j}\left|x_{i j}\right|$ 就像是regularization的限制。
结果如下:

(注:图中白色为墨水,黑色为空白)
Application
Deep Dream
CNN exaggerates what it sees.
CNN可以夸大图片中他所看到的东西。
比如:
可以把下图

变成下图(emmmm看着有点难受)

附上生成deep dream image的网站[2] .
Deep Style[3]
Given a photo, make its style like famous paintings.
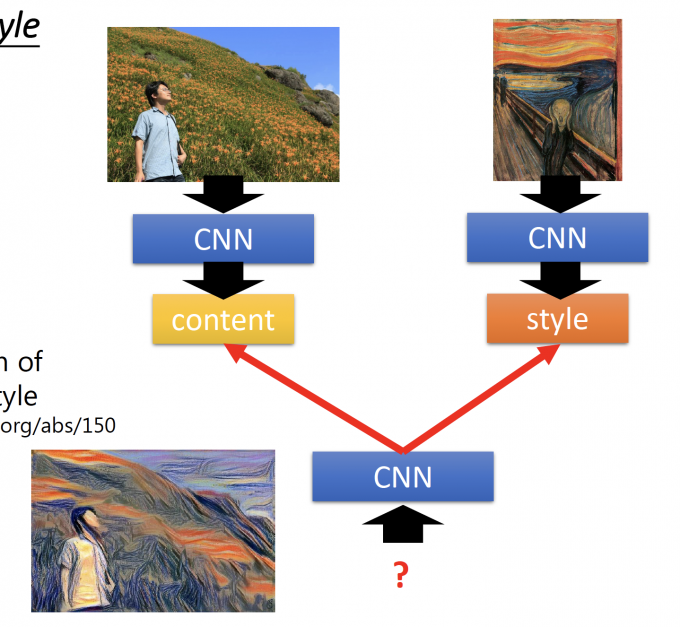
上图中,用一个CNN学习图中的content,用另一个CNN学习风格图中的style。
再用一个CNN使得输入的图像content像原图,风格像另一张图。
Playing Go
CNN 还可以用在下围棋中,如下图,输入是19 * 19的围棋局势(matrix/image),通过CNN,学出下一步应该走哪?
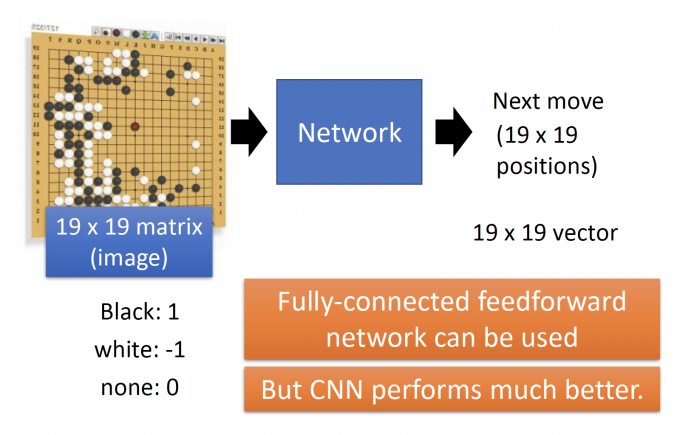
Why CNN playing Go?
下围棋满足以下两个property:
Some patterns are much smaller than the whole image.
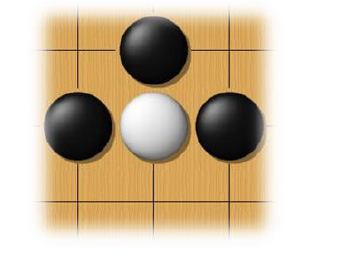
(围棋新手,博主只下赢过几次hhh)
如果白棋棋手,看到上图的pattern,上图的白子只有一口气了,被堵住就会被吃掉,那白棋棋手大概率会救那个白子,下在白棋的下方。
Alpha Go uese 5 * 5 for first layer.
The same patterns appear in different regions.

但如何解释CNN的另一结构——Max Pooling?
因为围棋的棋谱matrix不像image的pixel,subsample后,围棋的棋谱就和原棋谱完全不像了。
Alpha Go的论文中:Alpha Go并没有用Max Pooling。

所以,可以根据要训练的东西调整CNN模型。
Speech
可以用CNN学习Spectrogram ,即识别出这一时段说的是什么话。
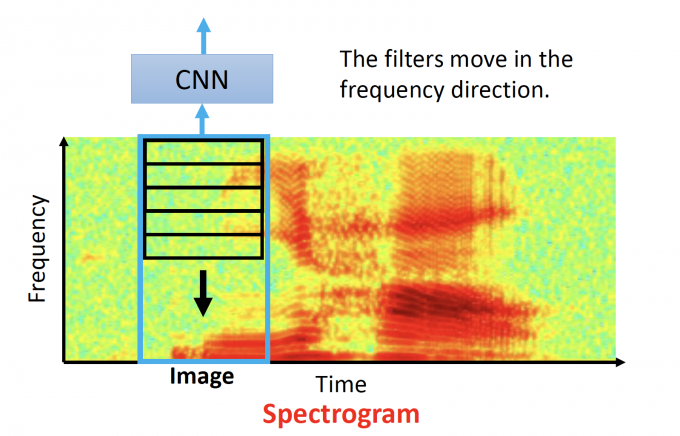
Text
CNN还可以用在文本的情感分析中,对句子中每个word embedding后,通过CNN,学习sentence表达的是negative 还是positive还是neutral的情绪。
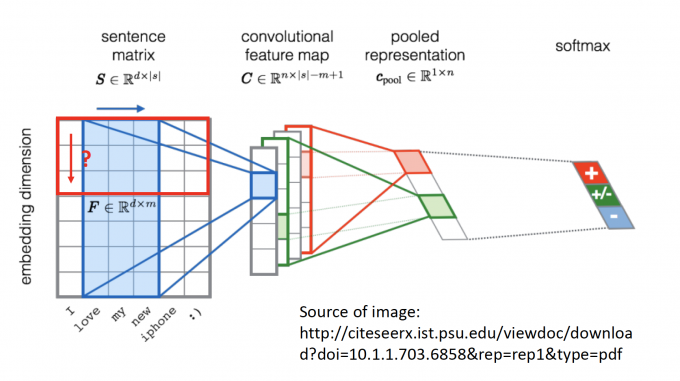
More
(挖坑…生命很漫长,学无止境QAQ)
The methods of visualization in these slides:
https://blog.keras.io/how-convolutional-neural-networks-see-the-world.html
More about visualization:
Very cool CNN visualization toolkit
The 9 Deep Learning Papers You Need To Know About
How to let machine draw an image
PixelRNN
Variation Autoencoder (VAE)
Generative Adversarial Network (GAN)
Reference
Deep Neural Networks are Easily Fooled: https://www.youtube.com/watch?v=M2IebCN9Ht4
deep dream generator: http://deepdreamgenerator.com/
A Neural Algorithm of Artistic Style: https://arxiv.org/abs/1508.06576
「机器学习-李宏毅」:Convolution Neural Network(CNN)

