「机器学习-李宏毅」:Recurrent Neural Network(RNN)
这篇文章中首先从RNN能解决什么问题入手,分析了RNN与一般NN的区别。
然后着重讲解了基于RNN的LSTM模型,包括LSTM的细节、和一般NN的区别,以及如何训练LSTM模型。
具体阐述了在模型(RNN类模型)训练过程中为什么会遇到剧烈抖动问题和如何解决抖动的工程解决方法。
Example application
Solt filling
先从RNN的应用说起,RNN能做什么?
RNN可以做智慧系统:
如下图中,用户告诉订票系统:”I would like to arrive Taipei on November 2nd”.
订票系统能从这句话中得到Destination: Taipei,time of arrival: November 2nd.
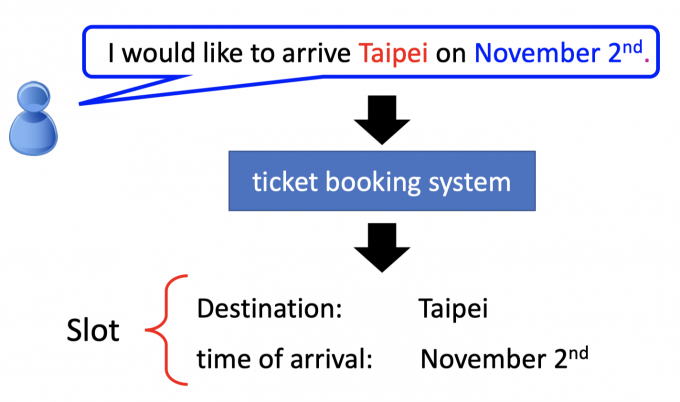
这个过程也就是Solt Filling (槽位填充)。
如果用Feedforward network来解决solt filling问题,输入就是单词,输出是每个槽位(slot)的单词,如下图。
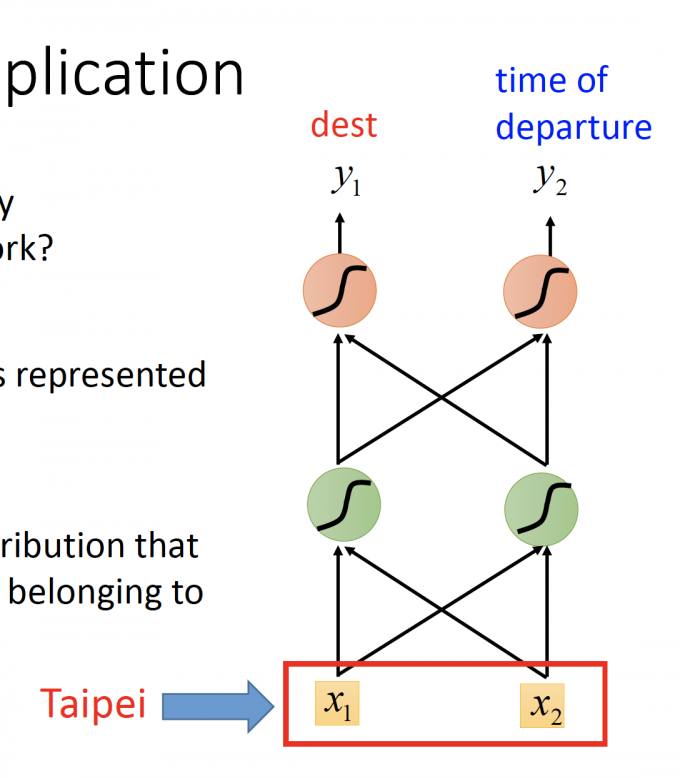
上图中,如何将word表示为一个vector?
Encoding
How to represent each word as a vector?
1-of-N encoding
最简单的方式是1-of-N encoding方式(独热方式)。
向量维度大小是整个词汇表的大小,每一个维度代表词汇表中的一个单词,如果该维度置1,表示这个维度代表的单词。
Beyond 1-of-N encoding
对1-of-N encoding方式改进。
第一种:Dimension for “Other”
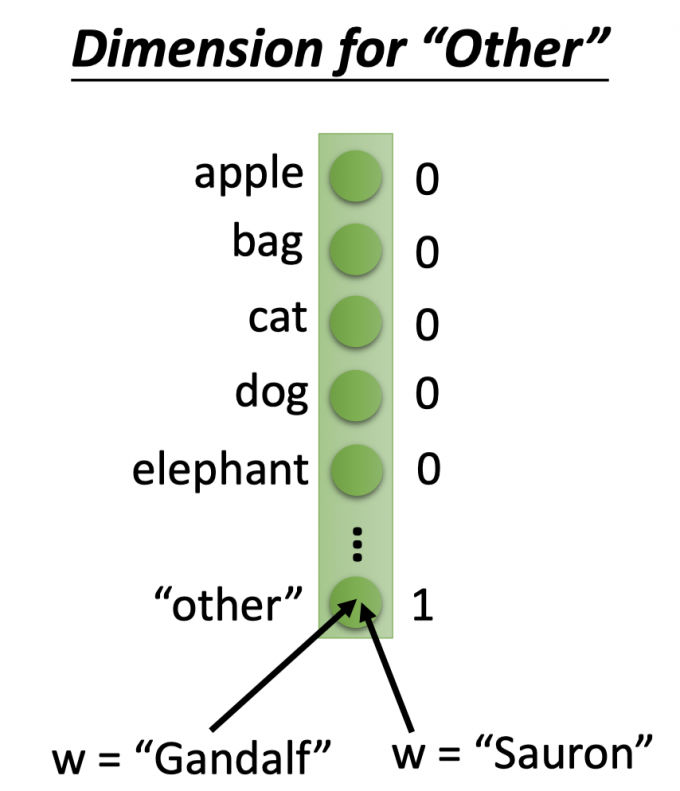
在1-of-N的基础上增加一维度——‘other’维度,即当单词不在系统词汇表中,将other维度置1代表该单词。
第二种:Word hashing
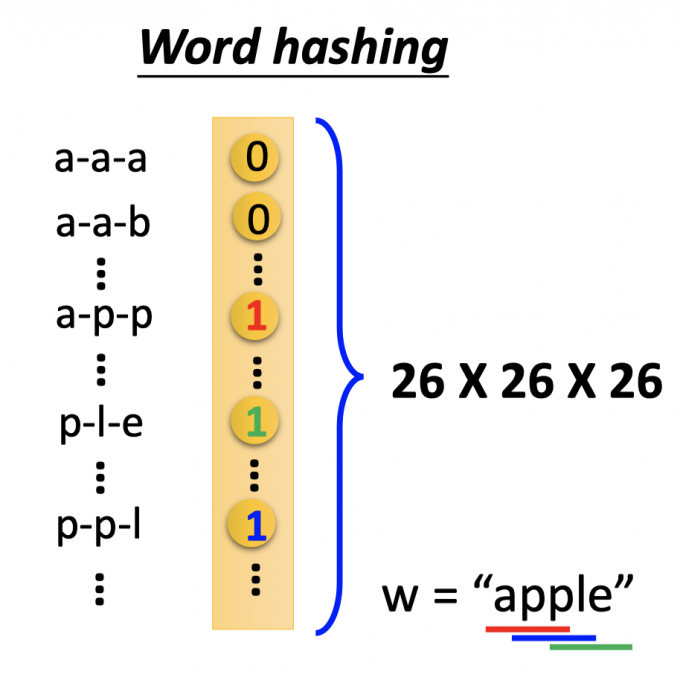
即便是增加了”other”维度,编码vector的维度也很大,用word hashing的方式将大幅减少维度。
以apple为例,拆成app, ppl, ple三个部分,如上图所示,vector中表示这三个部分的维度置1。
用这样的word hashing方式,vector的维度只有 $26\times 26\times26$ ,大幅减少词向量的维度。
Example
通过encoding的方式,单词用vector来表示,用前馈神经网络来解决solt filling问题。
如下图.
input:一个单词(encoding为vector)
output: input单词中属于该槽位(solts)的概率分布(vector)。

但用普通的前馈神经网络处理solt filling问题会出现下图问题:
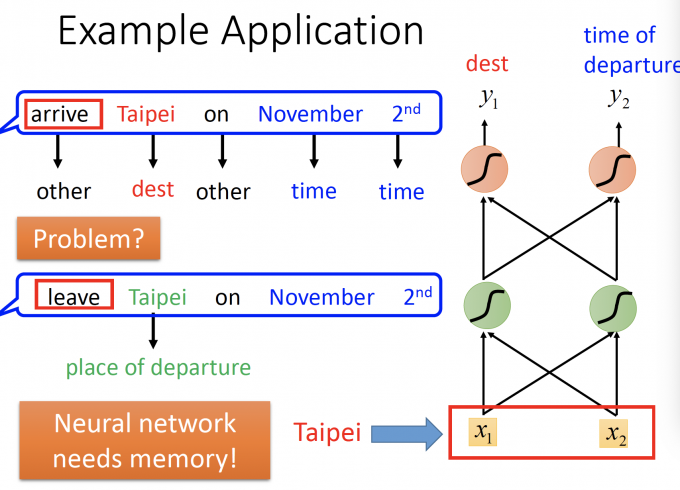
上图中,arrive Taipei on November 2nd 和 leave Taipei on November 2nd,将这两句话的每个单词(vector)放入前馈神经网络,得出的dest槽位都应该是Taipei。
但,通过之前的语意,arrive Taipei的Taipei应该是终点,而leave Taipei的Taipei是起点。
因此,在处理这种问题时,我们的神经网络应该需要memory,对该输入的上下文有一定的记忆存储。
Recurrent Neural Network(RNN)
Basic structure
因此,我们对一般的前馈神经网络加入记忆元件a, a 存储hidden layer的输出,同时a也作为下一次计算的输入部分,下图就是最基础的RNN模型。
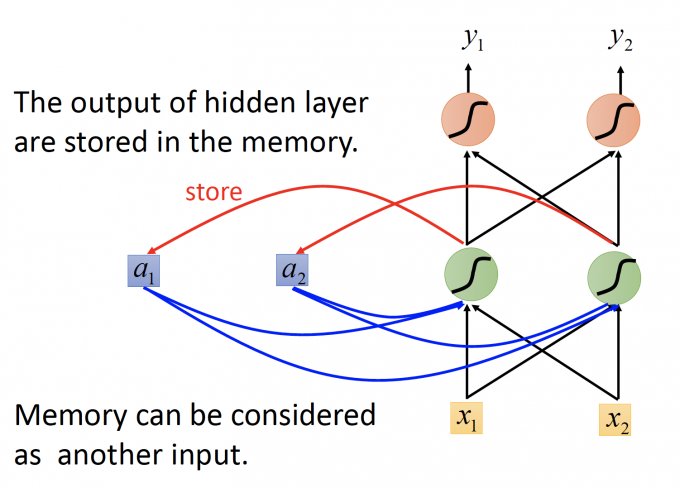
举一个例子来说明该过程:
Input sequence: $\begin{bmatrix}1 \ 1 \end{bmatrix}$ $\begin{bmatrix}1 \ 1 \end{bmatrix}$ $\begin{bmatrix}2 \ 2 \end{bmatrix}$ …
RNN模型如下图所示:所有的weight都是1,没有bias; 所有的神经元的activation function 都是线性的。
input : $\begin{bmatrix}1 \ 1 \end{bmatrix}$, 记忆元件初值 a1=0 a2=0.
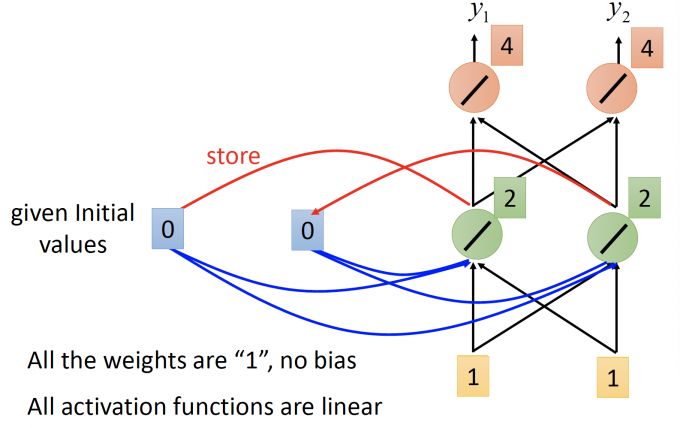
记忆元件也作为输入的一部分,hidden layer的输出为 2 2, 更新记忆元件的值.
output: $\begin{bmatrix}4 \ 4 \end{bmatrix}$ , 记忆元件存储值 a1=2 a2=2.
input : $\begin{bmatrix}1 \ 1 \end{bmatrix}$ , 记忆元件存储值 a1=2 a2=2.
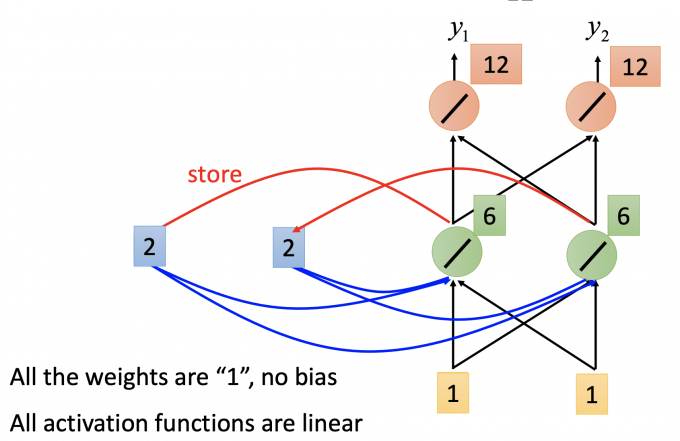
记忆元件也作为输入的一部分,hidden layer 的输出为6 6,更新记忆元件的值。
output: $\begin{bmatrix}12 \ 12 \end{bmatrix}$ , 记忆元件存储值 a1=6 a2=6.
这里可以发现,第一次和第二次的输入相同,但是由于有记忆元件的缘故,两次输出不同。
input : $\begin{bmatrix}2 \ 2 \end{bmatrix}$ , 记忆元件存储值 a1=6 a2=6.
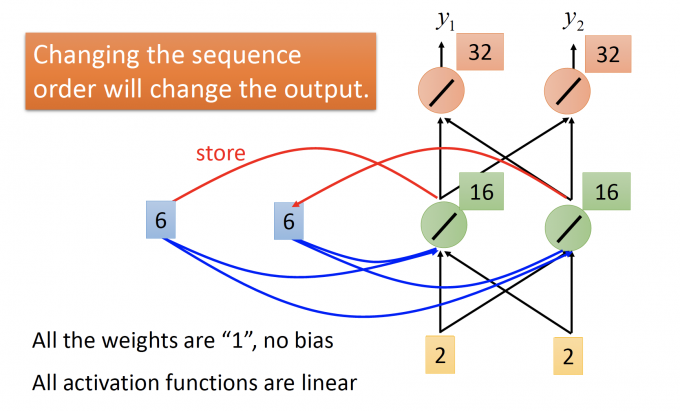
记忆元件也作为输入的一部分,hidden layer 的输出为16 16,更新记忆元件的值。
output: $\begin{bmatrix}32 \ 32 \end{bmatrix}$ , 记忆元件存储值 a1=16 a2=16.
RNN中,由于有memory,会和一般前馈模型有两个不同的地方:一是输入相同的vector,输出可能是不同的;二是将一个sequence连续放进RNN模型中,如果sequence中改变顺序,输出也大多不同。
用这个RNN模型来解决之前的solt filling问题,就可以解决上下文语意不同影响solt的问题。
将arrive Taipei on November 2nd的每个单词都放入同样的模型中。
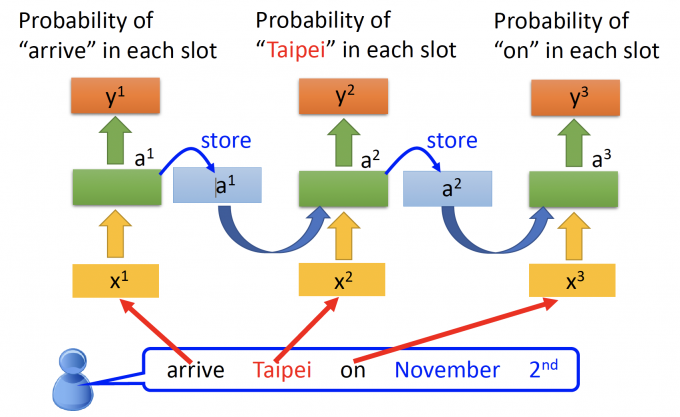
因此将RNN展开,如上图,像不同时间点的模型,但其实是不同时间点循环使用同一个模型。
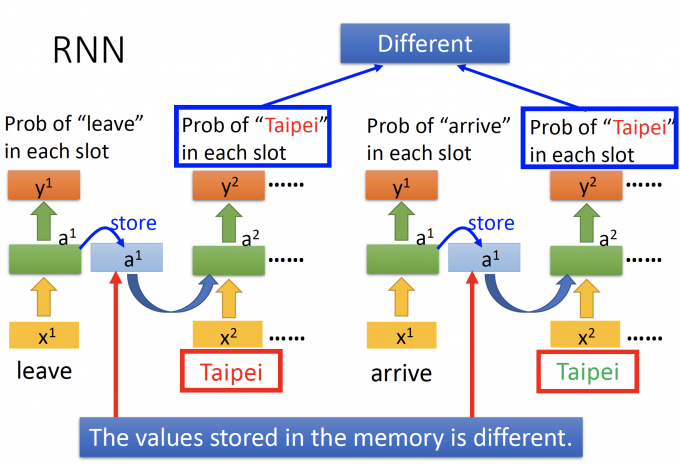
由于左边的前文是arrive,右边的前文是leave,所以存储在memory中的值不同,Taipei作为input的输出(槽位的概率分布)也不同。
Elman Network & Jordan Network
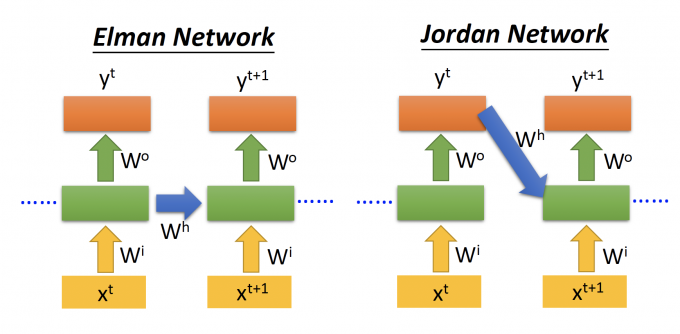
上文中只是RNN模型中的一种,即Elman Network,记忆元件存储的是上一个时间点hidden layer的输出。
而Jordan Network模型中,他的记忆元件存储的是上一时间点的output。
(据说,记忆元件中存储output的值会有较好的performance,因为output是有target vector的,因此能具象的体现放进memory的是什么)
Bidirectional RNN
上文中的RNN模型,记忆元件中存储的都是上文的信息,如果要同时考虑上下文信息,即是bidirectional RNN(双向RNN)。
模型如下图。
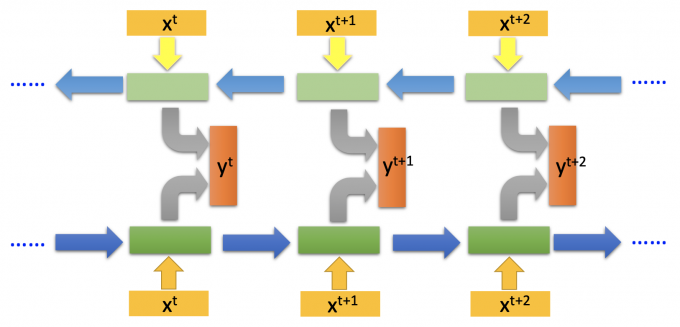
双向RNN的好处是看的范围比较广,当计算输出 $y^t$ 时,上下文的内容都有考虑到。
Long Short-term Memory(LSTM)
现在最常用的RNN模型是LSTM,Long Short-term Memory,这里的long是相当于上文中的RNN模型,因为上文提到的RNN模型都是short-term,即每一个时间点,都会把memory中的值洗掉,LSTM的long,就是会把memory的值保留的相对于久一些。
LSTM如下图,与一般NN不同的地方是,他有4个inputs,一个outputs。
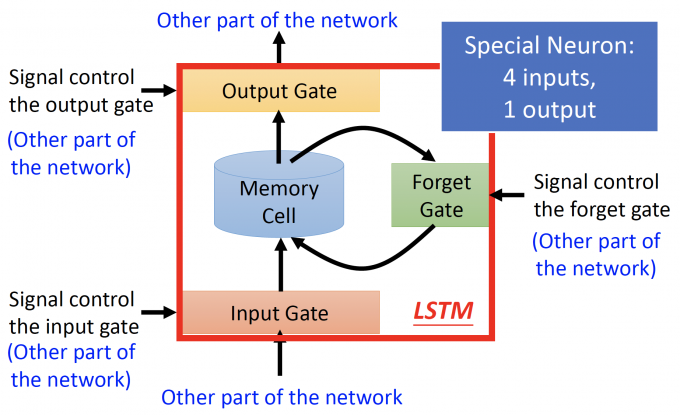
LSTM主要有四部分组成:
- Input Gate:输入门,下方箭头是输入,左方箭头是输入信号控制输入门的打开程度,完全打开LSTM才能将输入值完全读入,打开的程度也是NN自己学。
- Output Gate:输出门,上方箭头是输出,左方箭头是输入信号控制输出门的打开程度,同理,打开程度也是NN自己学习。
- Memory Cell:记忆元件。
- Forget Gate:遗忘门,右边的箭头是输入信号控制遗忘门的打开程度,控制将memory cell洗掉的程度。
LSTM
更详细的阐述LSTM的内部机制:
注意:
- $z_o,z_i,z_f$ 是门的signal control,其实就等同于一般NN中neuron的输入z,是scalar。
- gate其实就是一个neuron,通常gate neuron 的activation function f取 sigmod,因为值域在0到1之间,即对应门的打开程度。
- input/forget/output gate的neuron的activation function是f(sigmod function), input neuron的activation function是g。
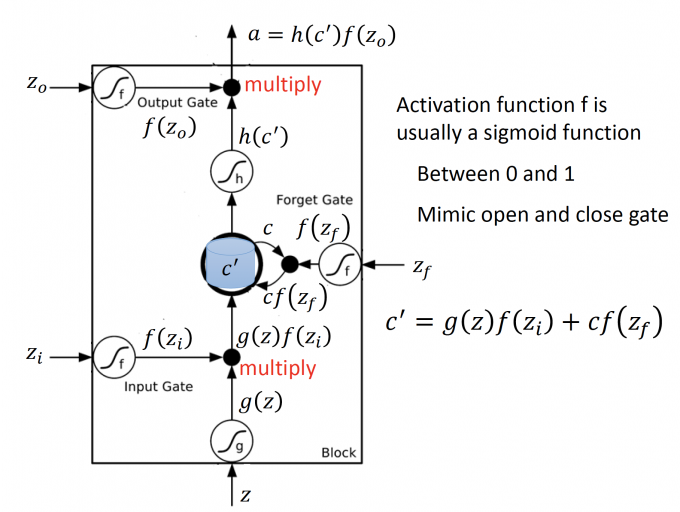
- input gate控制输入:$g(z)f(z_i)$
- input: z $\rightarrow$ $g(z)$
- input gate signal control: $z_i \rightarrow f(z_i)$
- multiply:$g(z)f(z_i)$
- forget gate 控制memory:$cf(z_f)$
- forget gate signal control: $z_f\rightarrow f(z_f)$
- 如果 $f(z_f)=1$ ,说明memory里的值保留;如果 $f(z_f)=0$ ,说明memory里的值洗掉。
- 更新当前时间点的memory(输入+旧的memory值) :$c’=g(z)f(z_i)+cf(z_f)$
- output gate 控制输出:$h(c’)f(z_o)$
- output: $c’ \rightarrow h(c’)$
- output gare signal control: $z_o \rightarrow f(z_o)$
- multiply: $h(c’)f(z_o)$
LSTM模型(trained)如下图:
输入序列为: $\begin{bmatrix}3 \ 1 \ 0 \end{bmatrix}$$\begin{bmatrix}4 \ 1 \ 0 \end{bmatrix}$ $\begin{bmatrix}2 \ 0 \ 0 \end{bmatrix}$ $\begin{bmatrix}1 \ 0 \ 1 \end{bmatrix}$ $\begin{bmatrix}3 \ -1 \ 0 \end{bmatrix}$
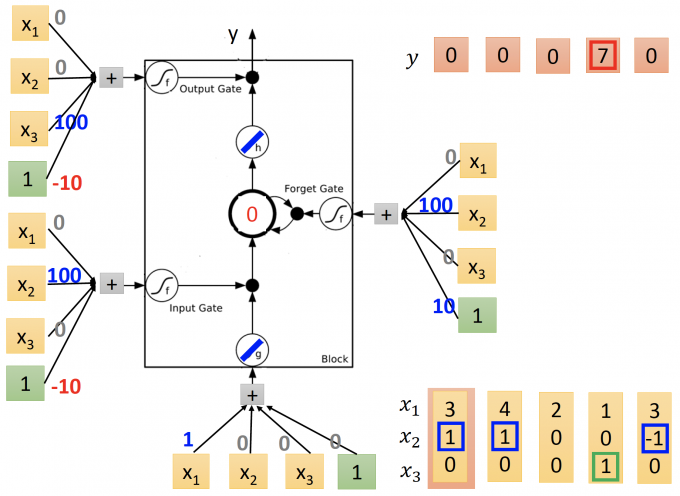
该LSTM activation function: g、h都为linear function(即输出等于输入),f为sigmod.
通过该LSTM的输出序列为: 0 0 0 7 0 0
(建议手算一遍)
Compared with Original Network
original network如下图:
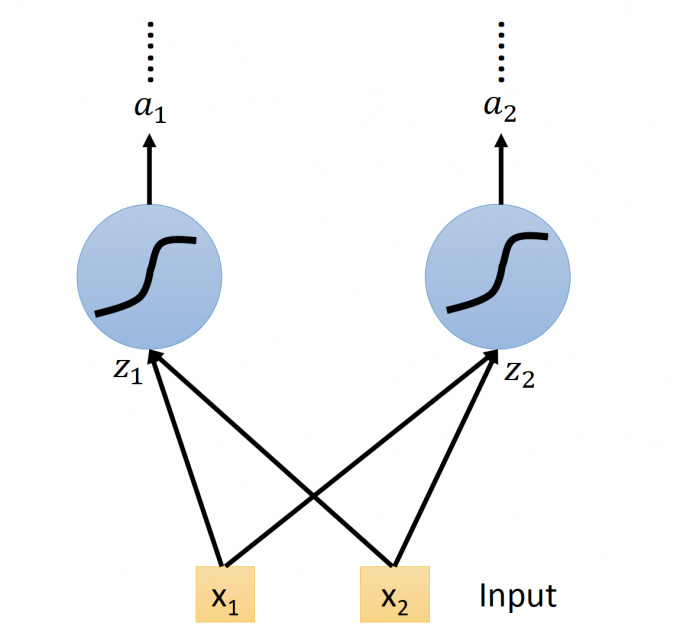
LSTM 的NN即用LSTM替换原来的neuron,这个neuron有四个inputs,相对于original network也有4倍的参数,如下图:
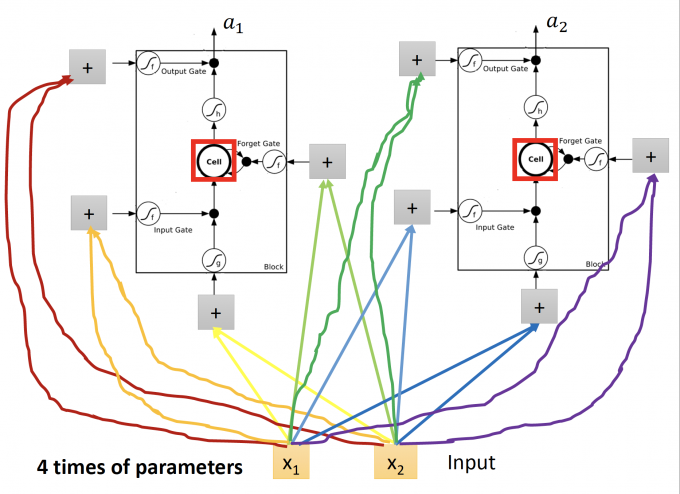
所以原来RNN的neuron换为LSTM,就是下图:
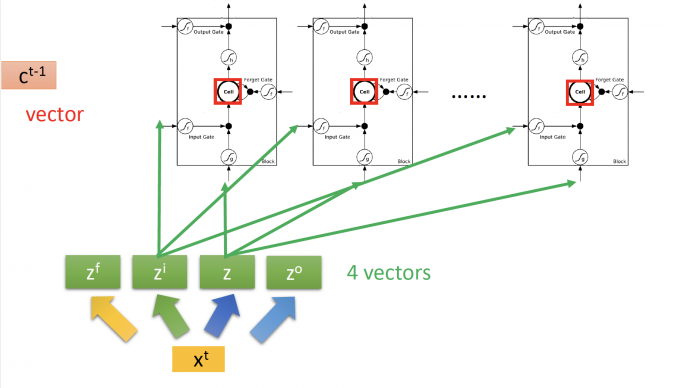
上图中:
这里的 $z^f,z^u,z,z^o$ 都是 $x^t \begin{bmatrix} \quad\end{bmatrix}$ 矩阵运算得到的vector, 因为上图中有多个LSTM,因此 $z^i$ 的第k个元素,就是控制第k个LSTM的input signal control scalar。所以,$z^f,z^u,z,z^o$ 的维度等于下一层neuron/LSTM的个数。
所以这里memory(cell)$c^t$ 也是一个vector,第k个元素是第k个LSTM中cell存储的值。
向量运算和scalar一样,LSTM细节如下图:
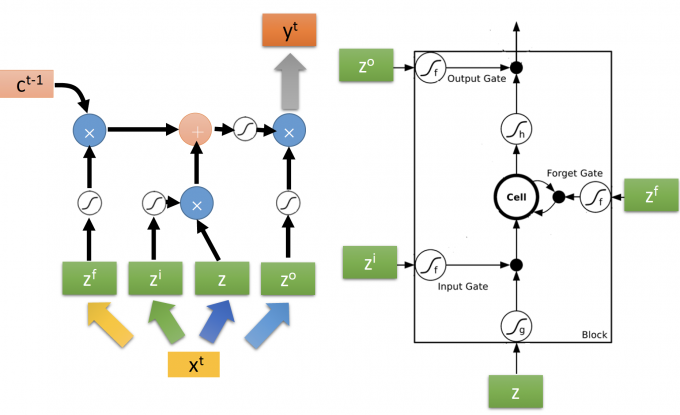
Extension:“peephole”
上小节的LSTM是simplified,将LSTM hidden layer的输出 $h^t$ 和cell中存储的值 $c^t$ 和下一时间点的输入 $x^{t+1}$ 一同作为下一时间点的输入,就是LSTM的扩展版”peephole”。
如下图:
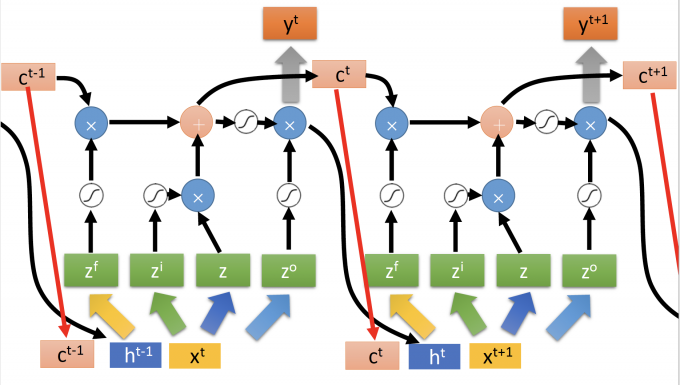
Multi-layer LSTM
多层的peephole LSTM如下图:
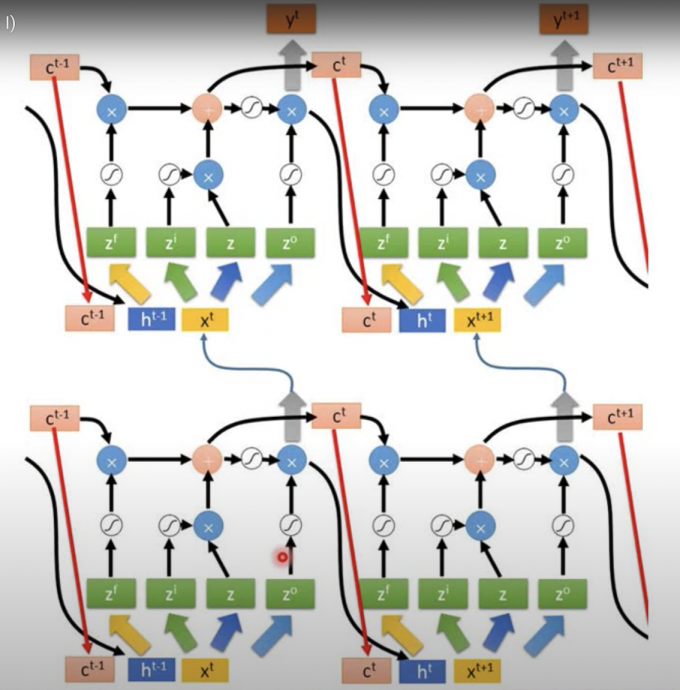
(:wtf 我到底看到了什么
不要怕:Keras、PyTorch等套件都有 “LSTM”,“GUR,”SimpleRNN“ 已实现好的layers.
Learning
训练RNN时,输入与target如下所示:
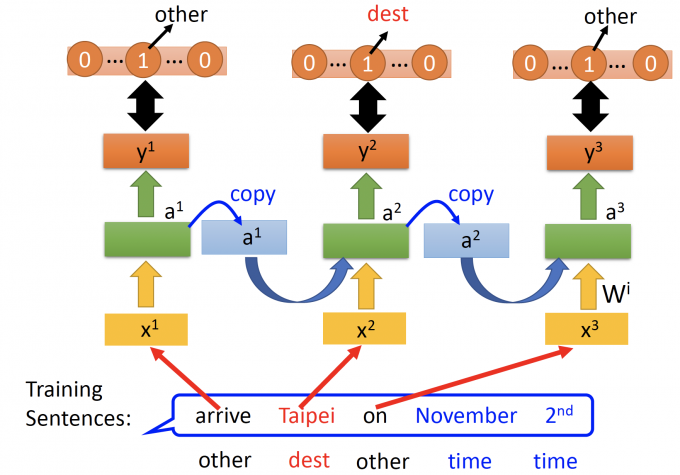
估测模型的好坏,计算RNN的Loss时,需要看作一个整体,计算每个时间点RNN输出与target的crossentropy的和。
训练也可同样用Backpropagation,但考虑到时间点,有一个进阶版的”Backpropogation through time(BPTT)”[1]。
RNN一般就用BPTT训练。
How to train well
not easy to train
RNN-based network is not always easy to learn.
但基于RNN的模型往往不太好训练,总是会出现下图中的绿色线情况(即抖动)。
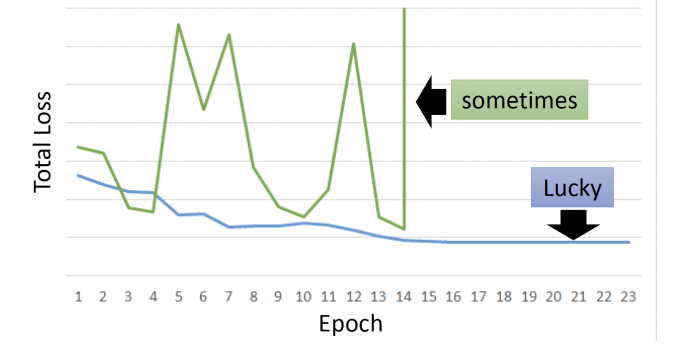
error surface is rough
error surface,即total loss在参数变化时的函数图。
会发现基于RNN的模型的error surface会长下图这个样子:有时很平坦(flat)有时很陡峭(steep)
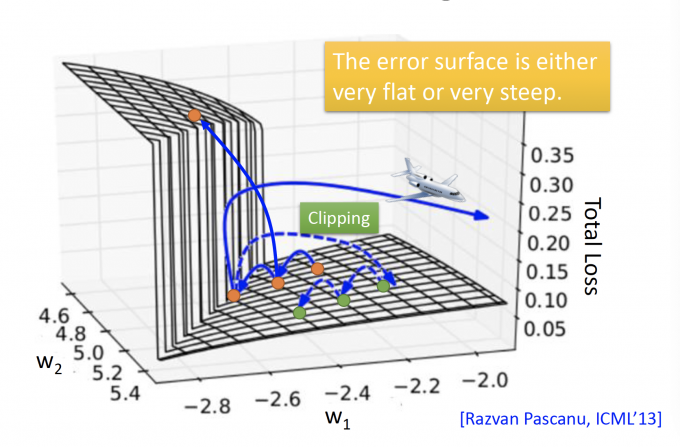
橙色点出发:
- 起初处在flat的位置。
- 随着一次次更新,gradient在变小,learning rate即会变大。
- 可能稍微不幸,就会出现跨过悬崖,即出现了剧烈震荡的问题。
- 如果刚好当前处在悬崖低,这时的gradient很大,learning rate也很大,step就会很大,飞出去,极可能出现segment fault(NaN).
Thomas Mikolv 用工程师的角度来解决这个问题,即当此时的gradient大于某个阈值(threshold)时,就不要让当前的gradient超过这个阈值(通常取15)。
这样处在悬崖低的橙色点,(Clipping路线),更新就会到绿色的,继续更新。
Why
为什么RNN模型会出现抖动的情况呢?
用下图这个简单例子说明(一般activation function用sigmod,而ReLu的performance一般较差):
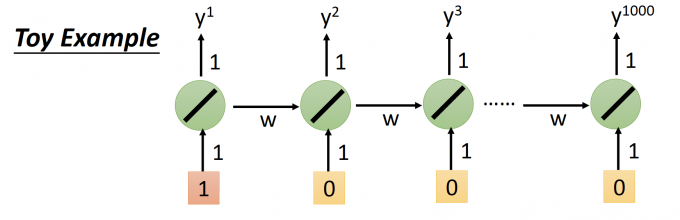
上图中,输入序列是1 0 0 0 …,memory连接下一个时间点的权重是w,可以轻易得到最后一个时间点的输出 $y^{1000}=w^{999}$ 。
上图中,循环输出1000次,如果w变化 $\Delta w$ ,看输出 $y^{1000}$ 的变化,来直观体现gradient 的变化:
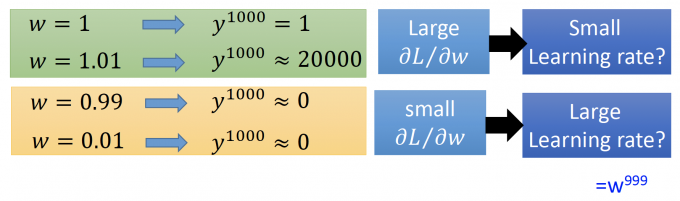
上图中,可以看出:
- 绿色部分:当w从1变化为1.01时, $y^{1000}$ 的输出变化即大,既有较大的gradient,理应有小的learning rate。
- 黄色部分:当w从0.99变化为0.01时, $y^{1000}$ 的输出几乎不变化,即有较小的gradient,理应有大大learning rate.
- 在很小的地方(0.01 到 1.01),他的gradient就变化即大,即抖动的出现。
Reason:RNN,虽然可以看作不同时间点的展开计算,但始终是同一个NN的权重计算(cell连接到下一个时间点的权重),在不同时间中,反复叠乘,因此会出现这种情况。
Helpful Techniques
- LSTM几乎已经算RNN的一个标准了,为什么LSTM的performance比较好呢。
为什么用LSTM替换为RNN?
:Can deal with gradient vanishing(not gradient explode).
可以解决gradient vanish的问题(gradient vanish problem 具体见 这篇文章2.1.1)
为什么LSTM可以解决gradient vanish问题
:memory and input are added.(LSTM的的输出与输入和memory有关)
: The influence never disappears unless forget gate is closed.(memory的影响可以很持久)
GRU[2](Gated Recurrent Unit):是只有两个Gate,比LSTM简单,参数更少,不容易overfitting
玄学了叭
More Applications
【待更新】
Many to One
Many to Many
Beyond Sequence
Seq2Seq
Auto-encoder-Text
Auto-encoder-Speech
Chat-bot
Reference
- BPTT
- GRU
「机器学习-李宏毅」:Recurrent Neural Network(RNN)

