「Cryptography-Boneh」:Stream Cipher 3

Stream Cipher的第三篇文章。

文章主要分为两部分，前部分逐步定义Secure PRG的定义，通过引入statistical test（统计测试）和Advantage（优势）得出当且仅当PRG is unpredictable,PRG is secure的结论。

后部分介绍了密码学中的一个重要概念Semantic Security的定义，通过引入 computationally indistinguishable(计算上不可区分)的概念给出定义，并证明了OTP的语意安全和在安全PRG条件下的流密码的语意安全，得出如果流密码中使用的PRG is secure,那么流密码就具备semantic security。

文章开头，也简单介绍了密码学中negligible和non-negligible的含义。

Negligible and non-negligible

In practice: $\epsilon$ is a scalar and

• $\epsilon$ non-neg: $\epsilon \geq 1/2^{30}$ (likely to happen over 1GB of data)
• $\epsilon$ negligible: $\epsilon \leq 1/2^{80}$ (won’t happen over life of key)

在实践中，$\epsilon$ 是一个数值，如果是non-neg不可忽略的话，大约在1GB的数据下就会发生，如果是可忽略的值，在密钥的生存周期内基本不会发生。

In theory: $\epsilon$ is a function $\varepsilon: Z^{\geq 0} \rightarrow R^{\geq 0}$ and

• $\epsilon$ non-neg: $\exists d: \epsilon(\lambda)\geq 1/\lambda^d$ ($\epsilon \geq 1/\text{poly} $, for many $\lambda$ )
• $\epsilon$ negligible: $\forall d, \lambda \geq \lambda_{d}: \varepsilon(\lambda) \leq 1 / \lambda^{d}$ ( $\epsilon \leq 1/\text{poly}$, for large $\lambda$ )

[0]（理论中，这个还不太理解，待补充。）

PRG Security Defs

Let $G:K\longrightarrow \{0,1\}^n$ be a PRG.

Goal: define what it means that

[ $k\stackrel{R}{\longleftarrow} \mathcal{K}$ , output G(k) ] is “indistinguishable” from [ $r\stackrel{R}{\longleftarrow} \{0,1\}^n$ , output r] .

【使得PGR的输出和真随机是不可区分的】（ $\stackrel{R}{\longleftarrow}$ 的意思是在均匀分布中随机取）

下图中，红色的圈是全部的 ${0,1}^n$ 串，按照定义是均匀分布。而粉色G()是PRG的输出，由于seed很小，相对于全部的 ${0,1}^n$ ，所以G()的输出范围也很小。

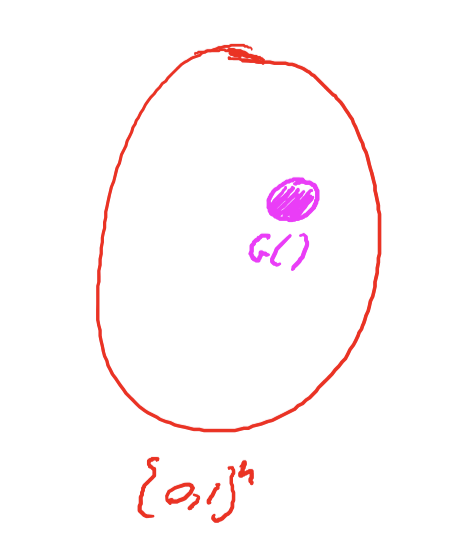
因此，attacker观测G(k)的输出，是不能和uniform distribution（均匀分布）的输出区分开。

这也就是我们所想构造的安全PGR的目标。

Statistical Tests

Statistical test on ${0,1}^n$ ：有一个算法A，$x\in{0,1}^n$ ,A(x) 根据算法定义输出”0”或”1”.

统计测试是自定义的。

Example：

1. A(x)=1 if $| \#0(x)-\#1(x)|\leq 10\cdot\sqrt{n}$

   【期望串中0、1的数目差不多，这样look random】

2. A(x)=1 if $|\#00(x)-\frac{n}{4}\leq10\cdot\sqrt{n}$

   【期望Pr(00)=1/4 ,串中00出现的概率为1/4，认为是look random】

3. A(x)=1if max-run-of-0(x) < 10·log(n)

   【期望串中0的最大游程不要超过规定值】

上面的第三个例子，如果输出为全1，满足上述的统计条件输出1，但全1串看起来并不random。

统计测试也由于是自定义的，所以通过统计测试的也不一定是random，其PRG也不一定是安全的。

所以，如何评估一个统计测试的好坏？

下面引入一个重要的定义advantage，优势。

Advantage

引入Advantage（优势）来评估一个统计测试的好坏。

Let G: $k \rightarrow \{0,1\}^n$ be a PRG and A a stat. test on ${0,1}^n$

【G是一个PRG，A是一个对01串的统计测试】

Define: the advantage of statisticaltest A relative to PRG G Adv$_\text{PRG}[A,G]$

$\text{Adv}_\text{PRG}[A,G]=|Pr[A(G(k))=1]-Pr[A(r)=1]|\in[0,1]$ , $k\stackrel{R}{\longleftarrow} \mathcal{K}, r\stackrel{R}{\longleftarrow}\{0,1\}^n$

【定义：Adv$_\text{PRG}[A,G]$ 为统计测试A对于PRG G的优势为统计测试以PRG作为输入输出为1的概率 减去 统计测试以truly random string 作为输入输出为1的概率】

• Adv close to 1 : 统计测试能区分PRG的输出和truly random string，即adversary可以利用区分PRG的输出和random的这一点从而破解系统。
• Adv close to 0 : 统计测试不能区分PRG的输出和truly random string, 即adversary认为PRG的输出和random别无二致。

Advantage 优势[1]

In cryptography, an adversary’s advantage is a measure of how successfully it can attack a cryptographic algorithm, by distinguishing it from an idealized version of that type of algorithm.Note that in this context, the “adversary” is itself an algorithm and not a person. A cryptographic algorithm is considered secure if no adversary has a non-negligible advantage, subject to specified bounds on the adversary’s computational resources (see concrete security).

在密码学中，adversary的优势是评估它通过某种理想算法破解一个加密算法的成功尺度。

这里的adversary是一种破解算法而不是指攻击者这个人。

当所有 adversary对该加密算法只有可忽略的优势时，该加密算法被认为是安全的，因为adversary只有有限的计算资源。

e.g.1 : A(x) = 0，统计测试A对PRG的任何输出都输出0，则Adv[A,G] = 0.

e.g.2 :

G: $k \rightarrow {0,1}^n$ satisfies msb(G(k))=1 for 2/3 of keys in K.

Define statistical test A(x) as : if[ msb(x)=1 ] output “1” else output “0”

【PRG G(k)的2/3的输出的最高有效位是1，定义统计测试A(x),输入的最高有效位为1输出1，否则输出0】

msb: most significant bit,最高有效位。

则 Adv[A,G] = | Pr[A(G(k))] - Pr[A(r)] | = 2/3 - 1/2 = 1/6

即 A can break the generator G with advantage 1/6, PRG G is not good.

Secure PRGs: crypto definition

Def: We say that G: $k \rightarrow {0,1}^n$ is secure PRG

if $\forall$ “eff” stat. tests A : Adv$_\text{PRG}$ [A,G] is “negligible”.

这里的”eff”,指多项式时间内。

这个定义，“所有的统计测试”，这一点难以达到，因此没有provably secure PRGs。

但我们有heuristic candidates.（有限的stat. test 能满足）

Easy fact: a secure PRG is unpredictable

证明命题： a secure PRG is unpredictable.

即证明其逆否命题： PRG is predictable is insecure。

suppose A is an efficient algorithm s.t. $\text{Pr}_{k\stackrel{R}{\longleftarrow}\mathcal{K}}[A(G(k))|_{1,...,i}=G(k)|_{i+1}]>\frac{1}{2} + \epsilon$ for non-negligible $\epsilon$ .

【 算法A是一个有效的预测算法， $\text{Pr}_{k\stackrel{R}{\longleftarrow}\mathcal{K}}[A(G(k))|_{1,...,i}=G(k)|_{i+1}]>\frac{1}{2} + \epsilon$ , $\epsilon$ 是不可忽略的值，即A能以大于1/2的概率推测下一位。】

Adversary能利用算法A来区分这个PRG和random依次来破解系统。

Define statistical test B as: B(x)=1 if $A(x|_{1,...,i})=x_{i+1}$ , else B(x)=0.

【定义一个统计测试B，如果预测算法A预测下一位正确输出1，否则输出0】

---

计算Adv$_\text{PRG}$ :

• $r\stackrel{R}{\longleftarrow}\{0,1\}^n$ : Pr[B(r) = 1] = 1/2
• $k\stackrel{R}{\longleftarrow}\{0,1\}^n$ : Pr[B(G(k)) = 1] = 1/2+ $\epsilon$
• Adv$_\text{PRG}$[B,G] = |Pr[B(r)=1] - Pr[B(G(k))=1] | > $\epsilon$

Adversary 能以 $\epsilon$ 的优势区分PRG和random，因此PRG 不安全。

所以，如果A是一个好的预测算法，那么B就是一个好的统计算法，Adversary就能通过B以 $\epsilon$ 的优势破解系统。

在此，证明了 if A can predict PRG, PRG is insecure $\Rightarrow$ A secure PRG is unpredictable.

Thm(Yao’82): an unpredictable PRG is secure

上节证明了A secure PRG is unpredictable.

在1982 Yao 的论文[2]中证明了其逆命题： an unpredictable PRG is secure.

G: $k \rightarrow {0,1}^n$ be PRG

“Thm“ : if $\forall i \in$ {0,…, n-1} PRG G is unpredictable at pos. i then G is a secure PRG.

【定理：如果在任何位置PRG都是不可预测的，那么PRG就是安全的】

Proof：

• A: 预测算法： $\forall i \quad\text{Pr}_{k\stackrel{R}{\longleftarrow}\mathcal{K}}[A(G(k))|_{1,...,i}=G(k)|_{i+1}]=\frac{1}{2} $
• B:统计测试： B(x)=1 if $A(x|_{1,...,i})=x_{i+1}$ , else B(x)=0.
• Adv$_\text{PRG}$[B,G] = |Pr[B(r)=1] - Pr[B(G(k))=1] | = 0

If next-bit predictors cannot distinguish G from random then no statistial test can!

【next-bit predictor指用预测算法的统计测试】

e.g.

Let G: $k \rightarrow {0,1}^n$ be PRG such that from the last n/2 bits of G(k) it is easy to compute the first n/2 bits.

Is G predictable for som i $\in$ {0, …, n-1} ?

: Yes.当n=2时，可以预测出第一位。

在此，可以得出结论：

Adversary不可区分PRG的输出和truly random string时被认为是安全的。

当且仅当PRG在任意位置不可预测时，PRG是安全的。

More generally: computationally indistinguishable

Let P1 and P2 be two distributions over ${0,1}^n$

Def : We say that P1 and P2 are computationally indistinguishable (denoted $P_1\approx_p P_2$)

If $\forall$ “eff” stat. tests A $\left|\text{Pr}_{x\leftarrow_{P_1}}[A(x)=1]-\text{Pr}_{x\leftarrow_{P_2}}[A(x)=1]\right|<\text{negligible}$ .

【P1,P2都是01串上的两个分布，且对任意的有效统计测试满足上式，则认为P1和P2两个分布在计算上不可区分，记做$P_1\approx_p P_2$】

所以，安全的PRG等价于G(k)的分布和均匀分布计算上不可区分，即 $\{\mathrm{k} \stackrel{\mathrm{R}}{\longleftarrow}{\mathrm{K}}: \mathrm{G}(\mathrm{k})\} \approx_{\mathrm{p}} \text { uniform }\left(\{0,1\}^{\mathrm{n}}\right)$

Semantic Security

上文详细了定义secure PRGs 的过程，本节的目标是定义”secure” stream cipher,安全流密码。

What is a secure cipher?

attacker abilities: obtains one ciphertext(唯密文攻击)

下面这些可能的安全需求是否能定义是安全的加密解密算法？

Possible security requirements：

1. attacker cannot recover secret key.

   attacker不能恢复密钥。

   E(k,m)=m直接输出明文，这个算法满足条件，但显然不安全。

2. attacker cannot recover all of plaintext.

   attacker对所有的明文都不可恢复。

   E(k, m0||m1) = m0||k $\oplus$ m1,该算法泄漏了一半的明文，不安全。

3. Shannon’s idea: CT should reveal no “info” about PT.

Recall Shannon‘s perfect secrecy

在Post not found: crypto2-StreamCipher1 这篇文章1.2.2 定义了perfect secrecy。

A cipher $(E,D)$ over $\mathcal{(K,M,C)}$ has perfect security if $\forall m_0,m_1 \in \mathcal{M}\ (|m_0|=|m_1|) \quad \text{and} \quad \forall c\in \mathcal{C} $

$$ Pr[E(k,m_0)=c]=Pr[E(k,m_1)=c] \qquad \text{where} \ k\overset{R}{\longleftarrow}\mathcal{K} $$

下面根据perfect security的定义逐步放宽条件定义：

Let (E,D) be a cipher over (K,M,C)

• 

  上图中的定义就是perfect security的定义，密钥加密m0和m1的分布完全相同。

  引入上文中的computationally indistinguishable（计算不可区分）的概率放宽条件，得到下面的定义。

• 

  密钥加密m0和m1的分布计算上不可区分。

• 但枚举所有的m0和m1的定义太强了，因此希望能让adversary列举计算上可列举的m0和m1.

Semantic Security for OTP

attack game

在定义OTP的semantic security （语意安全）之前，定义一个attack game。

Attack Game[3]: For a given cipher $\mathcal{E}$ = (E, D), defined over (K, M , C), and for a given adversary $\mathcal{A}$ , we define two experiments, Experiment 0 and Experiment 1. For b = 0, 1, we define

【定义一个adversary $\mathcal{A}$，两个实验也对应两个challenger，实验定义如下】

Experiment b:

• The adversary computes m0 , m1 ∈ M , of the same length, and sends them to the challenger.

  【adversary向challenger发m0和m1，他们长度相同】

• The challenger computes $k\stackrel{R}{\leftarrow}\mathcal{K}$, $c\stackrel{R}{\leftarrow}E(k,m_b)$, and sends c to the adversary.

  【实验b中challenger随机选取一个密钥k,用密钥加密mb,再将结果c返回给adversary】

• The adversary outputs a bit $\hat{b}\in$ { 0, 1 } .

  【adversary收到c，猜测c是加密m0还是m1的，输出 $\hat{b}$ 】

过程如下图所示，对于adversary $\mathcal{A}$ 来说，就像只有一个challenger，没有EXP(0)和EXP(1)的区别，因为它本来就是猜测challenger发送的c是加密m0所的还是m1所的。而对于challenger来说，才有EXP(0)和EXP(1)，在EXP(0)中，加密算法随机选择密钥加密m0返回，在EXP(1)中，加密算法随机选择密钥加密m1返回。

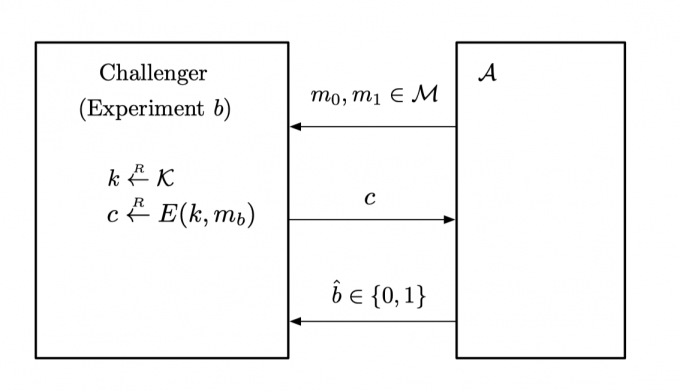
for b=0,1 $W_b$ = [event that $\mathcal{A}$ output 1 in experiment b].

【定义事件 $W_b$ 为在实验EXP(b)中$\mathcal{A}$ 输出1】

Def： $\mathcal{A}$‘s semantic security advantage with respect to $\mathcal{E}$ as

$$ \operatorname{Adv_{SS}}[\mathcal{A}, \mathcal{E}]:=\left|\operatorname{Pr}\left[W_{0}\right]-\operatorname{Pr}\left[W_{1}\right]\right| $$

【定义adversary $\mathcal{A}$ 对于cipher $\mathcal{E}$ 的语意安全优势为上式】

Note that in the above game, the events W0 and W1 are defined with respect to the probability space determined by the random choice of k, the random choices made (if any) by the encryption algorithm, and the random choices made (if any) by the adversary. The value Advss[ A , E] is a number between 0 and 1.

【注意：上面的游戏中，W0和W1的概率空间分布是与密钥的随机选择，加密算法的随机选择（该加密算法选择的是challenger0加密的m0还是challenger1加密的m1，adversary并不知道）和adversary的”随机”输出（按照adversary的判断方式的)有关的】

当challenger用随机密钥加密m0/m1时，观测adversary的行为是否相同，如果 $\left|\operatorname{Pr}\left[W_{0}\right]-\operatorname{Pr}\left[W_{1}\right]\right|$ 等于0，说明adversary无法区分这两个实验，如果 $\left|\operatorname{Pr}\left[W_{0}\right]-\operatorname{Pr}\left[W_{1}\right]\right|$ 等于1，则adversary可以区分这两个实验。

semantic security

Def：semantic security：A cipher $\mathcal{E}$ is semantially secure if for all efficient $\mathcal{A}$ , the value $\operatorname{Adv_{SS}}[\mathcal{A}, \mathcal{E}]$ is negligible.

当所有的有效的攻击算法 $\mathcal{A}$ 对于加密算法 $\mathcal{E}$ 的语意安全优势是可忽略的，则认为加密算法 $\mathcal{E}$ 是语意安全的。

即没有有效的攻击算法能区分对m0和m1对加密结果。

即任意密钥加密m0 m1的分布是计算上不可区分的，for all explicit m0, m1 $\in M:$ $\left\{\mathrm{E}\left(\mathrm{k}, \mathrm{m}_{0}\right)\right\} \approx_{\mathrm{p}}\left\{\mathrm{E}\left(\mathrm{k}, \mathrm{m}_{1}\right)\right\}$ .

example 1

Suppose efficient A can always deduce LSB of PT from CT.

【假设算法A总能从CT中推断出PT的最低有效位】

在下图cipher系统中，Adversary B算法向challenger发送的m0和m1，其发送的m0 m1特点是LSB(m0)=0,LSB(m1)=1。

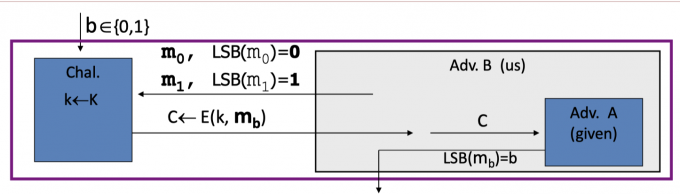
当adversary B收到密文c时，利用有效的算法A推断出对应明文的最低有效位LSB，如果是0，则输出0，即认为是实验0中challenger加密的m0，反之输出1。

adversary B对于cipher $\mathcal{E}$ 的优势是： $\operatorname{Adv_{SS}}[\mathcal{B}, \mathcal{E}]:=\left|\operatorname{Pr}\left[\text{EXP}(0)=1\right]-\operatorname{Pr}\left[\text{EXP}(1)=1\right]\right|=|0-1|=1$

所以该cipher $\mathcal{E}$ 不具有语意安全。

不仅是LSB，如果adversary能从密文中学到明文的任何一位，则该cipher都不具有semantic security。

example 2: OTP

OTP虽然不实用，但是具备perfect security，下面来证明OTP也具有semantic security。

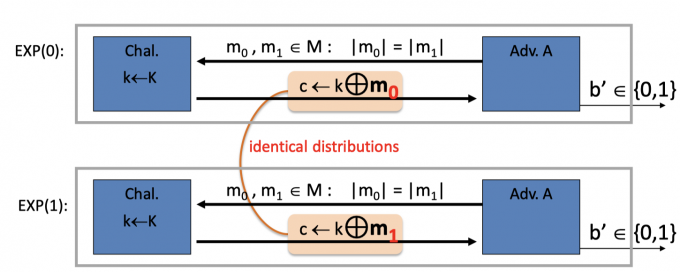
OTP的perfect security的性质是 $Pr[E(k,m_0)=c]=Pr[E(k,m_1)=c] \qquad \text{where} \ k\overset{R}{\longleftarrow}\mathcal{K}$ ，k和任意m异或都是均匀分布，因此上图中的 $\left\{\mathrm{E}\left(\mathrm{k}, \mathrm{m}_{0}\right)\right\} =\left\{\mathrm{E}\left(\mathrm{k}, \mathrm{m}_{1}\right)\right\}$ 是同分布。

For all A : $\operatorname{Adv}_{\operatorname{ss}}[A, \text { OTP }]=\mid \operatorname{Pr}\left[A\left(\mathbf{k} \oplus m_{0}\right)=1\right]-\operatorname{Pr}\left[A\left(\mathbf{k} \oplus m_{1}\right)=1\right]|=0$

Stream Ciphers are semantically secure

前面介绍了什么是安全的PRG，什么是语意安全，而流密码是否具有语意安全呢？

Thm: Let G: $k \rightarrow {0,1}^n$ is a secure PRG $\Rightarrow$ stream cipher E derived from G is semantic secure.

要证明以上定理：即要证明 $\forall$ sem. sec. adversary A $\operatorname{Adv}_{\operatorname{SS}}[A,E]$ is negligible.

如果 $\forall$ sem. sec. adversary A, $\exists$ a PRG adversay B s.t. $A d v_{s s}[A, E] \leq 2 \cdot A d v_{P R G}[B, G]$ 不等式成立，则定理得证。

因为G is a secure PRG, 根据定义，Adv$\text{PRG}$ [A,G] is negligible，所以左边$\operatorname{Adv}{\operatorname{SS}}[A,E]$ is negligible.

Proof: intuition

如果直观上证明Adv$_\text{PRG}$ [A,G] is negligible，如下图：

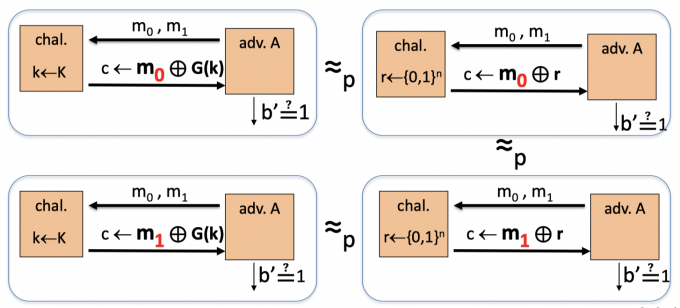
（上左上右下左下右：图1234，G(k):PRG 的输出， r: truly random string）

图1和图2中，由于G is a secure PRG，因此A计算上无法区分用G(k)和 random对m0加密的结果， 即$\ E(m_0,\mathrm{G}(\mathrm{k}))\} \approx_{\mathrm{p}} \{E(m_0,r)\}$ 。同理图三图四中，A计算上也无法区分用G(k)和random 对m1加密的结果，即 $\ E(m_1,\mathrm{G}(\mathrm{k}))\} \approx_{\mathrm{p}} \{E(m_1,r)\}$ 。

而图2图4中，是OPT的，即r和任意m异或都是均匀分布，满足 $\left\{\mathrm{E}\left(\mathrm{r}, \mathrm{m}_{0}\right)\right\} =\left\{\mathrm{E}\left(\mathrm{r}, \mathrm{m}_{1}\right)\right\}$ 是同分布.(图中应该可以写严格的等号)

所以可以直观得到 $\ E(m_0,\mathrm{G}(\mathrm{k}))\} \approx_{\mathrm{p}} E(m_1,\mathrm{G}(\mathrm{k}))\}$ ，即$\forall$ sem. sec. adversary A $\operatorname{Adv}_{\operatorname{SS}}[A,E]$ is negligible.

Proof

Let A be a sem. sec. adversary.

使用PRG，即$E(m,k) = m\oplus G(k)$ 时，如下图：

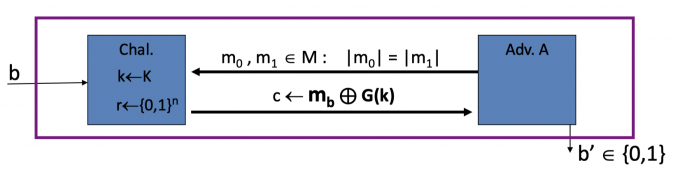
for b = 0,1 Wb = [event that b’=1]

$\operatorname{Adv}_{\operatorname{SS}}[A,E]=|\text{Pr}[W_0]-\text{Pr}[W_1]|$

---

使用OTP时，即 $E(m,r)=m\oplus r$ 时，如下图：

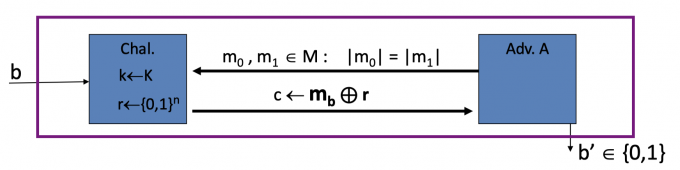
for b = 0,1 Rb = [event that b’=1]

$\operatorname{Adv}_{\operatorname{SS}}[A,OTP]=|\text{Pr}[R_0]-\text{Pr}[R_1]|=0$

---

如果把Pr[]的关系画在数轴上，如下图：

1. 根据OTP的semantic security ，已经得到 $|\text{Pr}[R_0]-\text{Pr}[R_1]|=\operatorname{Adv}_{\operatorname{SS}}[A,OTP]=0$ ，所以Pr[R0]=Pr[R1]。

2. 因为G是secure PRG，所以 $\exists$ adversary B满足 $|\text{Pr}[W_b]-\text{Pr}[R_b]|=\operatorname{Adv}_{\operatorname{PRG}}[B,G]$ ,如下图：

   

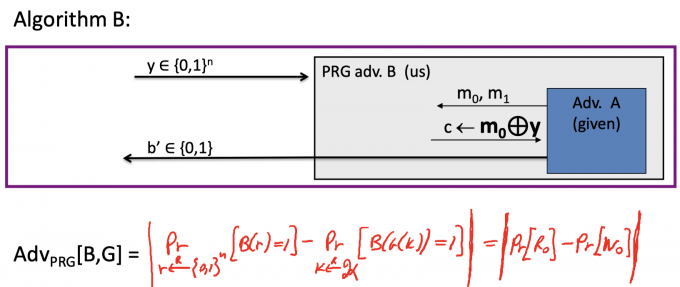
所以根据数轴的关系，Pr[W0]和Pr[W1]的距离最大为 $2 \cdot \mathrm{Adv}_{\mathrm{PRG}}[\mathrm{B}, \mathrm{G}]$ .

即 $\Rightarrow\mathrm{Adv}{\mathrm{SS}}[\mathrm{A}, \mathrm{E}]=\left|\operatorname{Pr}\left[\mathrm{W}{0}\right]-\operatorname{Pr}\left[\mathrm{W}{1}\right]\right| \leq 2 \cdot \mathrm{Adv}{\mathrm{PRG}}[\mathrm{B}, \mathrm{G}]$

证毕。

Summary

secure PRG 就是计算上无法区分G(k)的输出和truly random string。

semantic secure 就是从CT中无法得到PT的任何信息，在计算上无法区分任意m0和m1的加密结果。

而使用secure PRG的流密码是具有semantic security的。

reference

0. Negligible, super-poly, and poly-bounded functions.(Book p28)

1. Advantage Wiki定义：https://en.wikipedia.org/wiki/Advantage_(cryptography)

2. Yao’82: Theory and application of trapdoor functions:https://ieeexplore.ieee.org/document/4568378

3. Dan Boneh and Victor Shoup: A Graduate Course in Applied Cryptography