「LeetCode」：Array

   LeetCode an hour read (About 6985 words) 0 visits

8月某司实训+准备开学期末考，我可太咕了q w q…dbq，（希望）高产博主我.我..又回来了。

LeetCode Array专题，持久更新。（GitHub)

Array

27-Remove Elements

27-Remove Elements

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from typing import List


class Solution:

    def removeElement(self, nums: List[int], val: int) -> int:

        tot = 0
        for element in nums:
            if element == val:
                continue
            else:
                nums[tot] = element
                tot = tot + 1
        return tot

  1. Python的参数传递和函数返回值：

    1
    def removeElement(self, nums:List[int], val:int) -> int:

  2. 题目要求：

    “remove all instances of that value in-place and return the new length.”

    “Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.”

    “Confused why the returned value is an integer but your answer is an array?

    Note that the input array is passed in by reference, which means modification to the input array will be known to the caller as well.”

    题目要求是在原数组上删除数值，不能额外开新的空间存储数组。

    意思就是说，虽然函数返回的是一个数值，但实际返回答案是一个数组。

    因为数组的传递是指针传递，返回的是数组长度，则相当于返回了这个in-place的新数组。

26-Remove Duplicates from Sorted Array

26-Remove Duplicates from Sorted Array

Solution：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from typing import List


class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:

        tot = 0
        before = None
        for index in range(len(nums)):
            if nums[index] != before:
                nums[tot] = nums[index]
                before = nums[index]
                tot = tot + 1
            else:
                continue

        return tot

  1. 第一次提交的时候before = nums[0] - 1 报错了，原因是传入数组长度为0，下标越界。

    注意空数组的下标越界问题。

80-Remove Duplicates from Sorted Array II

80-Remove Duplicates from Sorted Array II

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from typing import List


class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        before = None
        before_cnt = 0
        length = 0
        for index in range(len(nums)):
            if nums[index] != before:
                nums[length] = nums[index]
                before = nums[index]
                length += 1
                before_cnt = 1
            else:
                before_cnt += 1
                if before_cnt <= 2:
                    nums[length] = nums[index]
                    length += 1
        return length

189-Rotate Array（S123）

189-Rotate Array

Problem:

简述题目大意，给一个列表nums，一个 $k$ 值，要求原址让列表循环右移 $k$ 位。

Solution:

其实以下三种做法时间空间复杂度差别不大，主要看个思路吧。

S Runtime Memory Language
S1 64ms 15.2MB pyhon3
S2 64ms 15.1MB python3
S3 116ms 15.1MB python3

S1-简单做法：空间换时间

时间复杂度：$\mathcal{O}(n)$

空间复杂度：$\mathcal{O}(n)$ ，循环右移时多开了一个数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
from typing import List
import queue

class Solution:
    def rotate(self, nums: List[int], k: int) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        length = len(nums)
        a = [0] * length
        for index in range(length):
            a[(index + k)%length] = nums[index]
        nums[:] = a

S2-利用数学同余关系

时间复杂度：$\mathcal{O}(n)$

空间复杂度：$\mathcal{O}(n)$ ，循环右移时只多开了一个变量。

原理：

定理[1]：

设 $m$ 是正整数，整数 $a$ 满足 $(a,m)=1$ ，$b$ 是任意整数。若 $x$ 遍历模 $m$ 的一个完全剩余系，则 $ax+b$ 也遍历模 $m$ 的一个完全剩余系。

由以上定理可以得知，设 $n$ 为列表长度， $x$ 是列表的下标，遍历 $n$ 的一个完全剩余系。

  • 如果 $(k,n)=1$ ， $kx$ 也遍历 $n$ 的一个完全剩余系。这种情况，列表下标通过 $k$ 的倍数的顺序连成一个环。

    ：只需要额外一个变量 $temp$ 存储移动占用的值。

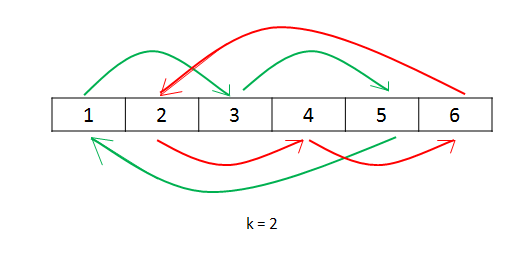
  • 如果 $(k,n)\neq 1$ ，那么 $kx$ 不会遍历一个 $n$ 的完全剩余系，会出现下图的情况（如绿色的线的元素的 $idx = kx+0$ ，红色线的元素都是 $idx=kx+1$ ），会在 $k$ 的某个剩余类一直循环。

    ：遍历每个 $k$ 的剩余类。 在每次循环移位时，需要记录该次循环的起始位，防止重复。

    wrcSVs.png 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def rotate(self, nums: List[int], k: int) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        length = len(nums)
        k %= length
        start = 0
        cnt = 0
        while cnt < length:
            current, prev = start, nums[start]
            while True:
                current = (current + k) % length
                prev, nums[current] = nums[current], prev
                cnt += 1
                if current == start:
                    break
            start += 1

S3-利用反转列表的思路

时间复杂度：$\mathcal{O}(n)$

空间复杂度：$\mathcal{O}(n)$

原理：

1
2
3
4
Original List                   : 1 2 3 4 5 6 7
After reversing all numbers     : 7 6 5 4 3 2 1
After reversing first k numbers : 5 6 7 4 3 2 1
After revering last n-k numbers : 5 6 7 1 2 3 4 --> Result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from typing import List


# Solution 3: Reverse
class Solution:

    def reverse(self, nums: list, begin: int, end: int) -> None:
        while begin < end:
            nums[begin], nums[end] = nums[end], nums[begin]
            begin += 1
            end -= 1

    def rotate(self, nums: List[int], k: int) -> None:
        n = len(nums)
        k %= n
        self.reverse(nums, 0, n-1)
        self.reverse(nums, 0, k-1)
        self.reverse(nums, k, n-1)

  1. Python用引用管理对象。

    1
    2
    int a1 = 1, *p = &a1;
    int a2 = 2, &b = a2;
    • 指针：指针变量是一个新变量，这个变量存储的是（变量a1的）地址，该地址指向一个存储单元。（该存储单元存放的是a1的值）。
    • 引用：引用的实质是变量的别名，所以a2和b实际是一个东西，在内存中占有同一个存储单元。

    所以python中交换对象可以直接a,b = b,a

  2. Python 列表的操作：切片。

41-First Missing Positive

41-First Missing Positive

Solution:

排一下序，维护一个expect变量就行了。

时间复杂度：$\mathcal{O}(n\log{n})$ ，题目没有卡常。

Runtime: 36 ms, faster than 70.96% of Python3 online submissions for First Missing Positive.

空间复杂度：$\mathcal{O}(n)$

Memory Usage: 13.8 MB, less than 69.19% of Python3 online submissions for First Missing Positive. 

1
2
3
4
5
6
7
8
9
10
11
12
13
from typing import List


class Solution:
    def firstMissingPositive(self, nums: List[int]) -> int:
        nums.sort()
        expect = 1
        for element in nums:
            if element == expect:
                expect += 1
            elif element > expect:
                return expect
        return expect

299-Bulls and Cows

299-Bulls and Cows

Problem:

题目大意是：给定两个相同长度的字符串，计算这两个字符串有多少个对应位数字相同，和多少个位置不对应但数字相同的个数。

Solution:

应用字符0-9本身数字的性质。

时间复杂度：$\mathcal{O}(n)$

空间复杂度：$\mathcal{O}(n)$ 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:

    def getHint(self, secret: str, guess: str) -> str:
        # 0-9 cnt for guess (expect the same digit)
        cnt = [0] * 10
        bulls = cows = 0
        g = lambda a: ord(a) - ord('0')
        for si, gi in zip(secret, guess):
            if si == gi:
                bulls += 1
            else:
                cnt[g(gi)] += 1

        for si, gi in zip(secret, guess):
            if si == gi:
                continue
            elif cnt[g(si)] > 0:
                cows += 1
                cnt[g(si)] -= 1
        output = "{}A{}B".format(bulls, cows)
        return output

  1. ord()函数和chr()函数

    ord()返回字符的ASCII码，chr函数返回ASCII码对应的字符。

  2. 浅析lambda表达式，匿名函数，类似于C语言的宏。

    格式：lambda [arg1[, arg2,...]] : expression

  3. 双变量同时遍历使用zip()函数

134-Gas Station（S12）

134-Gas Station

Problem：

题目大意是：有N个环形加油站，每个加油站能加油gas[i]，一个汽车起始油量为0，且从i个站开到第i+1个站需要花费cost[i]的油量。找出这个车能顺时针跑完一圈的起始点（如果有，则唯一），如果不能返回-1。

Solution：

Solution Runtime Memory Language
S1-简单做法 3244ms 14.9MB python3
S2-原理优化 104ms 14.8MB python3

S1-简单解法

时间复杂度：$\mathcal{O}(n^2)$ ，实际远达不到 $n^2$ ，算有一点贪心叭。

空间复杂度：$\mathcal{O}(n)$

该汽车从起点i能跑完的必要条件：

  • 起始点 gas[i] - cost[i] >= 0 。并且维护一个数组存放 gas[i] - cost[i] ，即这个站自给自足的油量余量。

  • 如果从满足条件1的起点开始跑一圈， 要求路程中的油量必须大于等于0。维护一个汽车当前总油量 $S$ （用前缀和维护），每跑过一段路程，都要求 $S>=0$ 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from typing import List


class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        n = len(gas)
        remain = []
        for g, c in zip(gas, cost):
            remain.append(g - c)
        for i in range(n):
            if remain[i] < 0:
                continue
            else:
                S = 0
                for j in range(n):
                    S += remain[(i + j) % n]
                    if S < 0:
                        break
                if S >= 0:
                    return i
        return -1

S2-对问题分析进行再简化

时间复杂度：$\mathcal{O}(n)$

空间复杂度：$\mathcal{O}(n)$ 

1
2
3
4
5
  i	: 0 1 2 3 4
g[i]: 1 2 3 4 5
c[i]: 3 4 5 1 2
g-c :-2-2-2 3 3
sum :-2-4-6-3 0

  • 如果 $S=\sum_{i=0}^{n-1} g[i]-c[i],S<0$ 那么一定无解， $S$ 称为总积累油量。

  • 如果 $S>=0$，如果有找出最优解的方法，则一定有解。

    1. 起点满足 $g[i]-c[i]>=0$ ，把这些点称为正余量点。

    2. 用 $\mathcal{O}(1)$ 算出从第 $i$ 个点出发到第 $n$ （n就是第0个点） 个点所积累的油量： $res[i] =S-sum[i-1]$ .即用总积累油量减去前 $i-1$ 段路程能积累的油量（一般积累为负）。(sum数组就是 g-c的前缀和)

    3. 对于满足起点要求 $g[i]-c[i]>=0$ 的所有点，计算从第 $i$ 个点出发到第 $n$ 个点到油量积累。那么有最大油量积累的点即为最优起始点。（题目规定如果存在，则点唯一）

    4. 因此，因为 $S$ 固定，只需要找到 $sum$ 数组中的最小值的下标，下标+1即是结果。

    • 证明其正确性：
      1. 如果满足 $g[i]-c[i]>=0$ 的上述点 $i,j（i<j)$ ，如果 $res[i]>=res[j]$ ，说明从 $i$ 到 $j$ 是正油量积累，贪心的思想，那肯定积累的油量越多越好， $i$ 比 $j$ 优。
      2. 如果 $res[i]<=res[j]$ ，说明从 $i$ 到 $j$ 是负油量积累，如果从 $i$ 点出发，到 $j$ 点就负油量了；如果从 $j$ 点出发，该车最后再跑 $i$ 到$j$ 段，因为保证了总积累油量是正，所以最后一定有足够的油量能跑完 $i$ 到 $j$ 段。
      3. 再证只要 $S>=0$ 则一定有解。是动态尝试起始点，( $i,j$ 都满足 $g[i]-c[i]>=0$ ）从点 $i$ 开始，跑到点 $j$ 时，如果该途中途有出现油量不够，那就把 $i$ 到 $j$ 的这段路程放到路途的后面来跑，等油量积累够了再跑这段。

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from typing import List


class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        n = len(gas)
        sum = 0
        remain = []
        for g, c in zip(gas, cost):
            remain.append(g - c)
            sum += g - c
        if sum < 0:
            return -1
        for i in range(1, n):
            remain[i] += remain[i - 1]
        min_idx = remain.index(min(remain))
        return (min_idx + 1) % n

  1. 前缀和
  2. list.index(value) 找出list中值为value 的第一个下标。
  3. min(list) 返回list中的最小值。

118-Pascal’s Triangle

118-Pascal’s Triangle

Problem:

给定一个数字，输出如下规则的值。

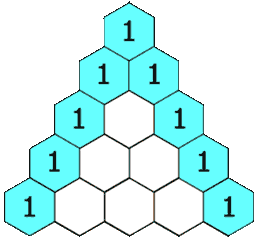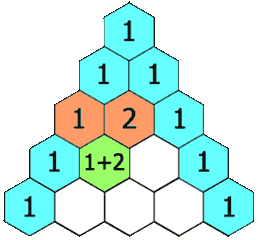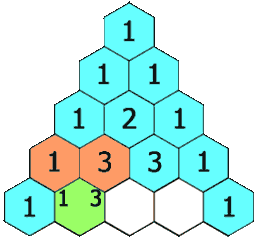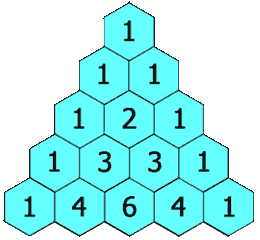
wyWI9s.gif

Solution：

注意边界吧。（不太喜欢这种题qwq

1
2
3
4
5
6
7
8
9
10
11
12
from typing import List


class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        ans = []
        for i in range(0, numRows):
            temp = [1] * (i+1)
            for j in range(1, i):
                temp[j] = ans[i-1][j-1] + ans[i-1][j]
            ans.append(temp)
        return ans

  1. Python 中的append会出现值被覆盖的情况：变量在循环外定义，但在循环中对该变量做出一定改变，然后append到列表，最后发现列表中的值都是一样的。

    因为Python中很多时候都是以对象的形式管理对象，因此append给列表的是一个地址。

119-Pascal’s Triangle II

119-Pascal’s Triangle II

Problem：

给定一个数字，输出某一行。

Solution：

1
2
3
4
5
6
7
8
9
10
11
12
from typing import List


class Solution:
    def getRow(self, rowIndex: int) -> List[int]:
        temp = [1]
        for i in range(0, rowIndex):
            for j in range(i, 0, -1):
                temp[j] += temp[j-1]
            temp.append(1)
        return temp

169-Majority Element

169-Majority Element

Problem:

给一串数字，找到出现次数大于 n/2 的数字。

Solution：

用字典计数。

1
2
3
4
5
6
7
8
9
10
11
12
13
from typing import List


class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        n = len(nums)
        cnt = {}
        for ele in nums:
            if ele in cnt:
                cnt[ele] += 1
            else:
                cnt[ele] = 1
        return max(cnt, key=cnt.get)
  1. 返回值最大/最小的键/索引。
    • 列表：
      • 最大值的索引：list.index(max(list))
      • 最小值的索引：list.index(min(list))
    • 字典：
      • 最大值的键：max(dict, key=dict.get)
      • 最小值的键：min(dict, key=dict.get)

229-Majority Element II

229-Majority Element II

Problem:

给一串数字，返回出现次数大于 n/3 的数字。

Solution：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from typing import List


class Solution:
    def majorityElement(self, nums: List[int]) -> int:
        n = len(nums)
        cnt = {}
        ans = []
        for ele in nums:
            if ele in cnt:
                cnt[ele] += 1
            else:
                cnt[ele] = 1
        for (k, v) in cnt.items():
            if v > n/3:
                ans.append(k)
        return ans

  1. 字典的实用方法：

    操作 实现方法
    删除字典元素 del dict['Name']
    清空字典所有条目 dict.clear()
    删除字典 del dict
    返回指定键的值，如果值不存在返回default的值 dict.get(key, default)
    如果键不存在字典中，添加键并将值设为default,于get类似 dict.setdefault(key, default=None)
    判读键是否存在 1. if k in dict 2. dict.has_key(key) 存在返回true
    以列表返回可遍历的（键，值）元祖数组 dict.items()
    以列表返回一个字典的所有键 dict.keys()
    以列表返回字典中的所有值 dict.values()
    返回最大值的键值 max(dict, key=dict.get)
    返回最小值的键值 min(dict, key=dict.get)

  2. 遍历字典的方法：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    # -*- coding:utf-8 -*-

    dict={"a":"Alice","b":"Bruce","J":"Jack"}

    # 实例一：键循环
    for i in dict:
        print "dict[%s]=" % i,dict[i]
    # 结果:
    # dict[a]= Alice
    # dict[J]= Jack
    # dict[b]= Bruce

    # 实例二：键值元组循环
    for i in  dict.items():
        print i
    # 结果:
    # ('a', 'Alice')
    # ('J', 'Jack')
    # ('b', 'Bruce')

    # 实例三：键值元组循环
    for (k,v) in  dict.items():
        print "dict[%s]=" % k,v
    # 结果:
    # dict[a]= Alice
    # dict[J]= Jack
    # dict[b]= Bruce

274-H-Index

274-H-Index

Problem:

给出研究人员论文的论文引用次数，计算它的H指数（有h篇论文的引用次数至少为h，剩下N-h篇论文的引用次数不超过h）。

Solution：

时间复杂度：$\mathcal{O}(n\log{n})$

空间复杂度：$\mathcal{O}(n)$

排序后，再二分。（感觉自己的二分写的有点丑qwq

还有一种思路是，排序完，从最大的h开始递减遍历，满足条件就返回。反正排序也要$\mathcal{O}(n\log{n})$ 的复杂度…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from typing import List


class Solution:
    def hIndex(self, citations: List[int]) -> int:
        n = len(citations)
        citations.sort()
        begin = 0
        end = n - 1
        while begin <= end:
            mid = (begin + end) >> 1
            h = n - mid
            if citations[mid] >= h:
                end = mid
                if begin == end:
                    return h
            else:
                begin += 1
        return n-begin
  1. 非递归写二分：while begin <= end

275-H-Index II

275-H-Index II

Problem:

和274一样，给了递增的论文引用数，希望能用指数时间返回H指数。

Solution：

啊，就二分鸭。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from typing import List


class Solution:
    def hIndex(self, citations: List[int]) -> int:
        n = len(citations)
        begin = 0
        end = n - 1
        while begin <= end:
            mid = (begin + end) >> 1
            h = n - mid
            if citations[mid] >= h:
                end = mid
                if begin == end:
                    return h
            else:
                begin += 1
        return n - begin

243-Shortest Word Distance

qwq 这道题还收费来着，于是于是就开了个中国区的会员（中国区的会员便宜好多啊！！）

243-Shortest Word Distance

Problem：

给定一串单词，单词1和单词2，计算单词1单词2在单词列表中的距离。

Solution：

Solution Runtime Memory Language
S1-二分查找 44ms 15.7MB python3
S2-线性维护 40ms 15.6MB python3

S1-二分查找

时间复杂度：$\mathcal{O}(n\log{n})$

空间复杂度：$\mathcal{O}(n)$

（最开始还很疑惑啥是单词距离…单词1和单词2可能在单词列表中重复出现）

计算出单词1和单词2在单词列表中出现的索引值列表，是递增有序的。

对于单词1索引列表中的每个值，在单词2索引列表中查找该值的lower_bound，计算距离。

同理，对于单词2索引列表中的每个值，也同样计算距离。

找出最小距离。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from typing import List


def lower_bound(a: list, x: int) -> int:
    n = len(a)
    begin = 0
    end = n - 1
    while begin <= end:
        mid = (begin + end) >> 1
        if a[mid] >= x:
            end = mid
            if begin == end:
                return begin
        else:
            begin += 1
    return -1


class Solution:
    ans = None

    def findShortest(self, li1: list, li2: list) -> None:
        for idx in li1:
            min_dis_idx = lower_bound(li2, idx)
            if min_dis_idx == -1:
                continue
            else:
                self.ans = min(self.ans, li2[min_dis_idx] - idx)
                if self.ans == 1:
                    return

    def shortestDistance(self, words: List[str], word1: str, word2: str) -> int:
        n = len(words)
        li1 = []
        li2 = []
        self.ans = n
        for idx in range(n):
            # li1 and li2 are ordered
            if words[idx] == word1:
                li1.append(idx)
            if words[idx] == word2:
                li2.append(idx)
        self.findShortest(li1, li2)
        if self.ans > 1:
            self.findShortest(li2, li1)

        return self.ans

S2-线性维护：

时间复杂度：$\mathcal{O}(n)$

空间复杂度：$\mathcal{O}(n)$

问题还能再简化，线性扫描单词列表，维护两个变量，单词1出现的最近索引，单词2出现的最近索引。扫描时计算距离，每当单词1或单词2出现时，就用另一个单词的最近索引计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from typing import List


class Solution:
    def shortestDistance(self, words: List[str], word1: str, word2: str) -> int:
        n = len(words)
        lst1 = None
        lst2 = None
        ans = n
        for idx in range(n):
            if words[idx] == word1:
                lst1 = idx
                if lst2 is not None:
                    ans = min(ans, lst1-lst2)
            if words[idx] == word2:
                lst2 = idx
                if lst1 is not None:
                    ans = min(ans, lst2-lst1)
        return ans

  1. C++中：

    lower_bound(begin, end, num)：返回num的下界，即大于等于num的第一个索引位置。

    upper_bound(begin, end, num)：返回num的上界，即大于num的第一个索引位置。

    Python中用二分实现这两个函数。

244-Shortest Word Distance II

244-Shortest Word Distance II

Problem:

和上题题干类似，计算单词距离，但是此问是每一个单词列表，可能有多个询问。

Solution：

对每一个单词列表，都可能有多个询问。

因此，之前243的解法每次询问都会遍历一遍单词列表。如果对每个单词列表询问数为 $M$ ，那么时间复杂度为 $\mathcal{O}(NM)$ ，会超时，所以希望能将单词列表的有关信息存下来，再用常数时间处理每一个询问。

这里的解法是用一个字典把每个单词出现的index列表存下来，键是单词，值是index列表。这个列表相对于单词列表的数目应该是远远小于的，因此用二重循环应该也能过吧（没有尝试二重循环解法）

这里有两种思路，一种是自己想的归并思路，还有一种是官方解答的思路，官方思路比归并的思路更优雅一些，问题抽象的更好。（代码差距不大，时间差距也不太大）

Solution Runtime Memory Language
S1-归并思路查询 96ms 20.8MB python3
S2-交叉跳跃查询 80ms 20.4MB python3

双指针：$i$ 指向列表1，$j$指向列表2.

S1-归并思路

归并思路：列表的值都是有序的，再把两个列表的值按归并的思想再排序，可以想成把点一个一个有序放在数轴上。

$i$指针前进的情况：（排序时，取列表1的下一个数字）

  1. $i+1<len1$ and $li1[i+1] < li[j]$
  2. $i+1<len1$ and $li1[i+1] < li[j+1]$
  3. $i+1 < len1$ and $j+1 == len2$ ($j$ 已无法移动)

其余情况：$j$ 移动。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from typing import List


class WordDistance:

    def __init__(self, words: List[str]):
        self.words = words
        self.len = len(words)
        self.dict = {}
        for index in range(self.len):
            word = words[index]
            if word in self.dict:
                temp = self.dict[word]
                temp.append(index)
            else:
                temp = [index]
                self.dict[word] = temp

    def shortest(self, word1: str, word2: str) -> int:
        ans = self.len
        li1 = self.dict[word1]
        li2 = self.dict[word2]
        len1 = len(li1)
        len2 = len(li2)
        i = j = 0
        while i < len1 and j < len2:
            ans = min(ans, abs(li1[i] - li2[j]))
            if ans == 1:
                return ans
            # i goes ahead
            if i + 1 < len1 and ((li1[i + 1] < li2[j]) or (j+1 == len2) or (j + 1 < len2 and li1[i + 1] < li2[j + 1])):
                i += 1
            else:
                j += 1
        return ans

S2-交叉比较

对于当前指向列表1和列表2的两个元素 $li1[i]$ 和 $li2[j]$ ，对 $li1[i]$来说，只需要和旁边的属于列表2的元素比较，对 $li2[j]$ 同理。

因此，当 $li1[i]>li2[j]$ 时，下一次的比较应该让 $j$ 指针前移一位，继续计算指针 $i$ 所指元素和其旁边的列表2的元素。同理，当 $li1[i]<li2[j]$ 时，下一次的比较应该让 $i$ 指针前移一位，继续计算指针 $j$ 和其旁边的列表1的元素。

具体移动如下图。

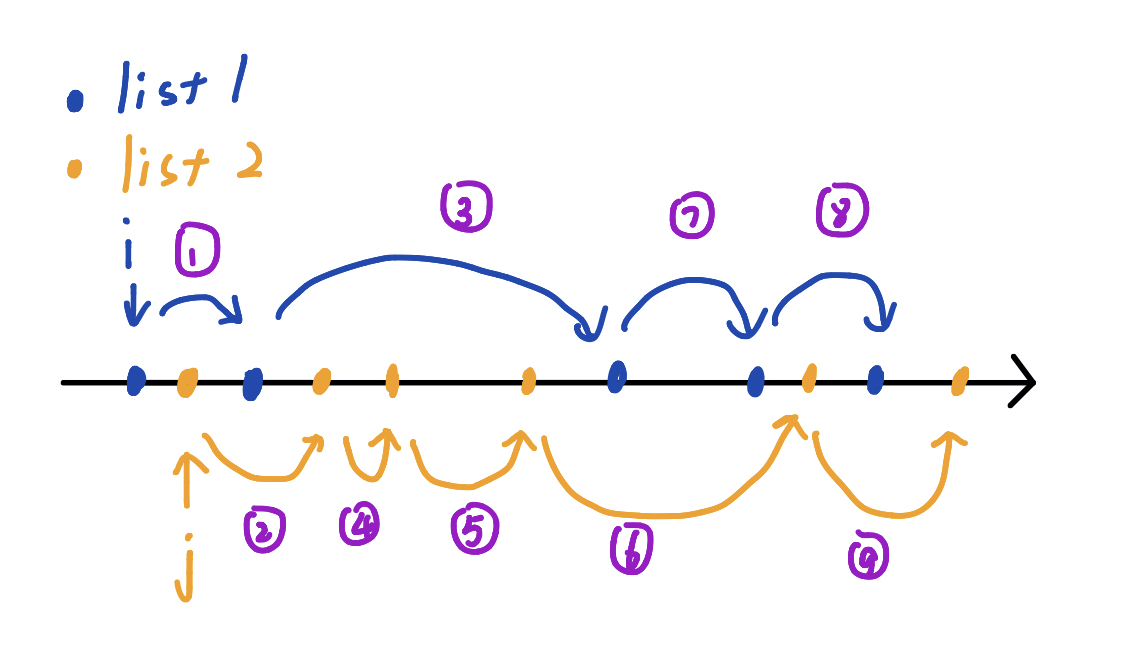
wIuW4K.jpg 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from typing import List


class WordDistance:

    def __init__(self, words: List[str]):
        self.words = words
        self.len = len(words)
        self.dict = {}
        for index in range(self.len):
            word = words[index]
            if word in self.dict:
                temp = self.dict[word]
                temp.append(index)
            else:
                temp = [index]
                self.dict[word] = temp

    def shortest(self, word1: str, word2: str) -> int:
        ans = self.len
        li1 = self.dict[word1]
        li2 = self.dict[word2]
        len1 = len(li1)
        len2 = len(li2)
        i = j = 0
        while i < len1 and j < len2:
            ans = min(ans, abs(li1[i] - li2[j]))
            if ans == 1:
                return ans
            # i goes ahead
            if li1[i] < li2[j]:
                i += 1
            else:
                j += 1
        return ans

277-Find the Celebrity

277-Find the Celebrity

Problem:

已有know(i, j) API，判断i是否知道j，i是名人的充要条件是其他所有人知道i，而i不知道其他所有人。

Solution：

两种思路，第一种较为直观，使用二重循环，但剪枝多，远达不到 $\mathcal{O}(n^2)$ ，第二种稍做优化。因此两种解法差距不太大。

提交时间 运行时间 内存消耗 语言
S几秒前 1896ms 13.6MB python3
5 分钟前 1772ms 13.6MB python3

S1-直观思路

时间复杂度：远不到 $\mathcal{O}(n^2)$

用了二重循环，但剪枝很多，所以远达不到 $\mathcal{O}(n^2)$ 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution:
    def findCelebrity(self, n: int) -> int:
        for i in range(n):
            fg = True
            # i knows j ?
            for j in range(n):
                if i == j:
                    continue
                if knows(i, j):
                    fg = False
                    break
            if not fg:
                continue
            # j knows i ?
            for j in range(n):
                if i == j:
                    continue
                if not knows(j, i):
                    fg = False
                    break
            if not fg:
                continue
            else:
                return i
        return -1

S2-排除法

时间复杂度：$\mathcal{O}(n)$

排除i：根据know(i, j)=True 可以认为i不是名人，j可能是名人。

对于n-1个关系，最后从n个人中选出一个可能的人，再根据名人的充要条件去判断他是否是名人。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
    def findCelebrity(self, n: int) -> int:
        celebrity = 0
        for i in range(1, n):
            if knows(celebrity, i):
                celebrity = i
                continue
        for i in range(n):
            if celebrity == i:
                continue
            if (not knows(celebrity, i)) and knows(i, celebrity):
                continue
            else:
                return -1
        return celebrity

245-Shortest Word Distance III

245-Shortest Word Distance III

Problem:

题意增加了两个单词可能相同，分两种情况就好了。

Solution：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from typing import List


class Solution:
    def shortestWordDistance(self, words: List[str], word1: str, word2: str) -> int:
        n = len(words)
        ptr1 = None
        ptr2 = None
        ans = n
        if word1 == word2:
            for idx in range(n):
                if words[idx] == word1:
                    ptr1, ptr2 = idx, ptr1
                if (ptr1 is not None) and (ptr2 is not None):
                    ans = min(ans, ptr1-ptr2)
        else:
            for idx in range(n):
                if words[idx] == word1:
                    ptr1 = idx
                if words[idx] == word2:
                    ptr2 = idx
                if (ptr1 is not None) and (ptr2 is not None):
                    ans = min(ans, abs(ptr1-ptr2))
        return ans

217-Contains Duplicate[E]

217-Contains Duplicate

Problem:

判断数组中有无重复元素出现。

Solution：

1
2
3
4
5
6
7
8
class Solution:
    def containsDuplicate(self, nums: List[int]) -> bool:
        S = set()
        for i in nums:
            if i in S:
                return True
            S.add(i)
        return False

219-Contains Duplicate II[E]

219-Contains Duplicate II

Problem:

判断数组中是否有两个相同的值，他们的索引之差小于等于k。

Solution：

存放出现该值的最近的索引，扫一遍。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:
        dict = {}
        n = len(nums)
        for i in range(n):
            if nums[i] not in dict:
                dict.setdefault(nums[i], i)
            else:
                if i - dict[nums[i]] <= k:
                    return True
                dict[nums[i]] = i
        return False

4-Median of Two Sorted Arrays[H] （2S）

4-Median of Two Sorted Arrays[H]

Problem:

给两个排好序的数组，返回一个中位数

Solution：

S 运行时间 内存消耗
S1 $\mathcal{O}(m+n)$ ：92ms 14.3MB
S2 $\mathcal{O}(\log(m+n))$ ：52ms 13.3MB

S1:

归并排序的做法。

时间复杂度：$\mathcal{O}(m+n)$ 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from typing import List


class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        n1 = len(nums1)
        n2 = len(nums2)
        median1 = median2 = None
        i = j = 0
        tot = 0
        while i < n1 or j < n2:
            if (i < n1 and j < n2 and nums1[i] <= nums2[j]) or (i < n1 and j >= n2):
                tot += 1
                if tot == (n1 + n2)//2:
                    median1 = nums1[i]
                if tot == (n1 + n2)//2 + 1:
                    median2 = nums1[i]
                    break
                i += 1
            else:
                tot += 1
                if tot == (n1 + n2) // 2:
                    median1 = nums2[j]
                if tot == (n1 + n2) // 2 + 1:
                    median2 = nums2[j]
                    break
                j += 1
        if (n1 + n2) % 2 == 1:
            return median2
        else:
            return (median1 + median2)/2

S2:

二分的思路

时间复杂度：$\mathcal{O}(\log(m+n))$

一、首先讨论一个数组的中位数，数组有n个元素，如果n为奇数，则第(n+1)/2个是中位数；如果n为偶数，则第(n+1)/2和第(n+2)/2的平均值为中位数。

回到本题，因为是两个数组，如果根据奇偶性分类讨论就过于麻烦了，所以将两种情况统一以简化解题思路。

即无论n是奇数还是偶数，数组的中位数都是第(n+1)/2和第(n+2)/2的平均数。

回到本题，设数组1有n个元素，数组2有m个元素，则中位数为两个数组的有序序列的第(n+m+1)/2个和第(n+m+2)/2个的平均数。

二、因此，题目需要求解的问题改为求这两个有序数组的有序序列的第k个数。

二分思想：两个数组分别找第k/2个数，（假设都存在），比较，如果第一个数组的这个数小于第二个数组，说明第k个数肯定不在第一个数组的前k/2个数中，因此就可以直接去掉数组1的前k/2个元素，查找有序序列的第k-k/2个数；同理，如果大于，则说明第k个数肯定不在第二个数组的前k/2个数中，去掉数组2的前k/2个元素。

使用一个数组起始指针l1和l2来实现数组的“去掉”前k/2个元素。

设数组1的元素个数为n，数组2的元素个数为m。

递归函数Find(l1, l2, k)：查找起始指针为l1, l2的两个有序数组的第k个数。

  • 讨论边界情况，有数组为空的情况。即 l1 == n 或者 l2 == m .

    如果第一个数组已为空，则直接返回第二个数组的第k个数；

    同理，如果第二个数组为空，则直接返回第一个数组的第k个数。

  • 两个数组都不为空的情况。即 l1 < n 或者 l2 < m .

    • 递归边界： k == 1 ,即返回 nums1[l1] 和 nums2[l2] 中较小的那一个。

    • 数组长度边界：即有数组的剩余元素个数小于 k/2 ，那么拿出来比较的就应该是数组的最后一个元素。

      维护两个值 k1 和 k2 来分别表示用两个数组的第 k1和k2个来比较。

      (k1 k2都小于等于k/2)

      1
      2
      3
      # to avoid the rest length of nums1/nums2 is shorter than k//2
      k1 = k//2 if l1+k//2 <= n else n-l1
      k2 = k//2 if l2+k//2 <= m else m-l2

    • 比较nums1[l1+k1-1] 和 nums2[l2+k2-1] 的大小，递归：

      1. 相等：

        如果 k-k1-k2 == 0 说明nums1的前k1个和nums2的前k2个就是有序序列的前k个，返回 nums1[l1+k1-1] 。

        否则，（即某一个数组的剩余长度小于k/2），分别去掉两个数组的前k1和k2个数，递归调用 Find(l1+k1, l2+k2, k-k1-k2) 。

      2. nums1[l1+k1-1] > nums2[l2+k2-1]

        说明可以去掉数组2的前k2个数，递归调用 Find(l1, l2+k2, k-k2)

      3. nums1[l1+k1-1] > nums2[l2+k2-1]

        说明可以去掉数组1的前k1个数，递归调用 Find(l1+k1, l2, k-k1)

Code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution:
    def __init__(self):
        self.nums1 = None
        self.nums2 = None

    def findKthOfTwo(self, l1: int, l2: int, k: int) -> int:
        nums1 = self.nums1
        nums2 = self.nums2
        n = len(nums1)
        m = len(nums2)
        # nums1 is empty
        if l1 == n:
            return nums2[l2+k-1]
        # nums2 is empty
        if l2 == m:
            return nums1[l1+k-1]
        # both not empty
        if k == 1:
            return nums1[l1] if nums1[l1] <= nums2[l2] else nums2[l2]
        # to avoid the rest length of nums1/nums2 is shorter than k//2
        k1 = k//2 if l1+k//2 <= n else n-l1
        k2 = k//2 if l2+k//2 <= m else m-l2
        if nums1[l1+k1-1] == nums2[l2+k2-1]:
            return nums1[l1+k1-1] if k-k1-k2 == 0 else self.findKthOfTwo(l1+k1, l2+k2, k-k1-k2)
        elif nums1[l1+k1-1] > nums2[l2+k2-1]:
            return self.findKthOfTwo(l1, l2+k2, k-k2)
        else:
            return self.findKthOfTwo(l1+k1, l2, k-k1)

    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        n = len(nums1)
        m = len(nums2)
        self.nums1 = nums1
        self.nums2 = nums2
        # median: the average of (n+m+1)//2 th  and  (n+m+2)//2 th
        return (self.findKthOfTwo(0, 0, (n+m+1)//2) + self.findKthOfTwo(0, 0, (n+m+2)//2)) / 2

reference

  1. 《信息安全数学基础》 2.2同余类和剩余系。

「LeetCode」：Array

https://f7ed.com/2020/09/15/LeetCode_array/

Author

f7ed

Posted on

2020-09-15

Updated on

2020-10-09

Licensed under

CC BY-NC-SA 4.0

 

Like this article? Support the author with

Comments

Email me
×