「Math」:Entropy, Cross-Entropy and DL-Divergence
在机器学习中,常用cross-entropy来作为模型的损失函数,这篇文章将阐述信息学中的entropy(熵)是什么,cross-entropy(交叉熵)又是什么,KL-Divergence和entropy、cross-entropy的关系是什么?
如何具象的理解这些概念?
在开始阅读这篇文章之前,先提及一下香农对bit的定义,香农认为bit是用来消除信息的不确定性的。
bit:uncertainty divided by 2.
原视频 讲的很好,本文只是在此基础上对一些总结,方便理解物质化(马原.jpg)。
公式总概
bit:用来消除信息的不确定性
Entropy(熵): $H(p)=-\sum_i p_i\log(p_i)$
度量概率分布的平均信息量(即不确定性)。值越大,不确定性越大。
Cross-Entropy(交叉熵): $H(p,q)=-\sum_i p_i\log(q_i)$
度量两个分布的相似程度(一般 $p$ 为真实分布,$q$为预测分布),值越大,两个分布越不相似。
KL-Divergence(KL散度,也叫相对熵) :$D_{KL}(p|q)=H(p,q)-H(q)$
度量交叉熵超过熵的那一部分。
Entropy-熵
实例1:
sunny和rainy的发生的概率都是0.5,天气预报预测明天的天气为sunny,将sunny消息发给用户。
该条消息不管多长,有用的信息其实只有1个比特,即uncertainty divided by 2.
实例2:
有八种不同的天气,发生的概率相同,当天气预报将预测消息发送给用户时。
该条消息能使得uncertainty divided By 8.即有用信息为3个比特。
实例3:
sunny发生的概率为0.75,rainy的概率为0.25,如果天气预测明天的天气:
将这个例子理解为抽球游戏,盒子里有3个红球(表示sunny天气),1个白球(rainy天气)。
事件 $X$ 表示为在盒子里抽中球的颜色,可得知抽中红球的概率为0.75,抽中白球的概率是0.25。
抽中哪个球是不确定的,即uncertainty 如果原来是4,即不知道将抽中这四个球中的哪一个。
如果抽中白球,那该信息表示:就是那4个球中的唯一一个白球,uncertainty 从原来的4变为1,即 uncertainty divided by 4.表示该信息,需要有用比特, $\log_2(4)=\log_2(1/0.25)=2$ 个比特来表示。即抽打白球的情况的不确定性更大,需要更多的比特来消除不确定性,来表示白球的发生。所以该条信息中只有2个比特是useful information.
如果抽中红球,该信息表示为:是那3个红球中的一个,uncertainty 从原来的4变为3
(如果和抽中白球的情况统一,最后的确定发生的uncertainty都表示为1,即在没有抽之前,抽到红球的uncertainty为 $1/0.75=4/3$ )
即uncertainty divided by 4/3.表示该信息需要有用 $\log_2(4/3)=\log_2(1/0.75)=-\log_2(0.75)=0.41$ 比特来表示。即抽到红球的情况不确定性没有那么大,只需要较少比特即可消除不确定性,来表示红球的发生。所以该条信息中只有0.41个比特是useful information.
这里也可以看出,如果一个事件的发生的概率越小(越不可能发生),即对该事件发生的不确定性越大,但一旦发生了,所携带的信息量就会很大,因为需要用更多的比特来消除不确定性。
回到本例子:
如果预测天气为rainy,将预测消息发给用户,则该条消息包含2比特($\log_2(1/0.25)=-\log_2(0.25)=2$)的有用信息,即对rainy天气发送的不确定性更大,需要更多的比特来消除不确定性。
如果预测天气为sunny,因为在预测之前,用户对sunny发生的可能性就没有那么大,因此只需要0.41比特($\log_2(1/0.75)=-\log_2(0.75)$)来消除不确定性。
那平均下来,气象局发送的平均信息量为 $0.75\times 0.41+0.25\times2=0.81$ bits.
因此我们用 $\log_2(1/p)=-\log_2p$ 来表示事件发生时所携带的信息量。(或者说需要这么多信息量来消除事件发生的不确定性)
用 $-\sum_i{p_i}\log_2{p_i}$ 来表示该事件的平均信息量(概率分布的不确定性),这就是信息熵(Entropy)。
Entropy:
$$
H(p)=-\sum_i pi\log_2(p_i)
$$
熵越大,说明携带的平均信息量越多,即不确定性越强,需要越多的比特来消除不确定性。所以熵是用来衡量不确定性的量。
和化学中衡量混乱程度的熵,是类似的。
Cross-Entropy-交叉熵
例1:
从上面的实例2来看,即8中天气发生概率相同,对天气表示进行信息编码,为下图:
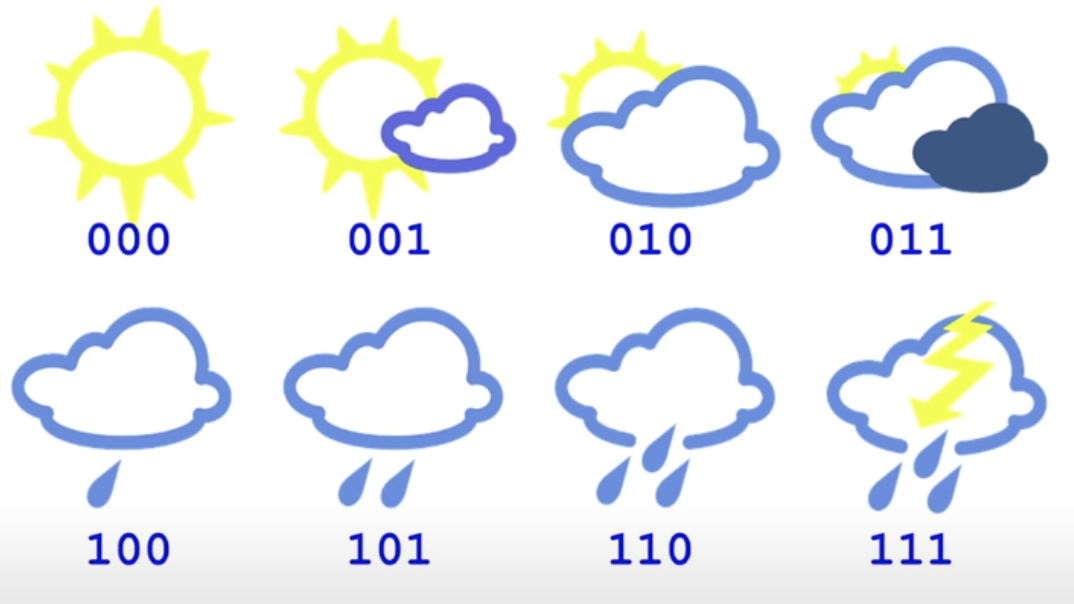
entropy为3bits,而cross-entropy(交叉熵),也就是消息(比特流)的平均长度,为3bits.
例2:
但如果8种天气发生的可能性为下图:

算出来的entropy为2.23bits,即平均信息量为2.23bits。
如果仍是用这样的编码,cross-entropy为3bits,就多出一些冗余信息量。
例3:
如果换一种编码方式:

算出来的cross-entropy为 $0.35 \times2+0.35\times2+0.1\times3+…+0.01\times5=2.42$ bits,就非常接近entropy=2.23bits。
说明这种编码方式冗余量很小,非常接近真实的概率分布所包含的平均信息。
例4:
如果天气的概率分布变为下图,entropy不变仍然为2.23bits:

那么算出来的cross-entropy为 $0.01\times2+0.01\times 2+0.04\times3+…+0.35\times5=4.58$ bits,远大于entropy的值。说明这种编码方式冗余量很大。
换一种角度看例4,把信息编码认为是预测的概率分布,例4点编码表示的分布如下:

Cross-Entropy:
$$
H(p,q)=-\sum_i p_i\log(q_i)
$$
所以cross-entropy可以理解为信息/比特流的平均长度。
如果预测的概率分布非常接近真实的概率分布,那比特流的平均长度也会非常接近原分布的平均信息量。
如果预测的概率分布 $q$ 和真实分布 $p$ 完全一样,那么cross-entropy等于entropy。
所以cross-entropy可以用来衡量两个概率分布的相似程度。
用在机器学习中用作评判模型好坏的损失函数,度量模型预测分布和真实分布的相似程度。
KL-Divergence-KL散度
而如果预测的概率分布和真实分布不同,那么cross-entropy的值就会大于entropy的值,超过的部分就叫做relative entropy(相对熵),也就是KL-Divergence(Kullback-Leibler Divergence,KL散度)
即可以得到等式:$\text{Cross-Entropy = Entropy+KL-Divergence}$
则KL-Divergence:
$$
\begin{align}
D_{KL}(p|q)=H(p,q)-H(p) &= -\sum_i p_i\ln q_i - \sum_i p_i\ln p_i \
&= -\sum_i p_i \ln \frac{p_i}{q_i} \
&= \sum_i p_i \ln \frac{q_i}{p_i}
\end{align}
$$
Reference
「Math」:Entropy, Cross-Entropy and DL-Divergence

