「Algebraic ECCs」: Lec2 Linear Codes and Finite Fields
Linear Algebra over $\{0, 1\}$
- Generator Matrices
- Parity-Check Matrices
Linear Algebra not Working over $\{0, 1, 2, 3\}$
Finite Fields and Linear Codes
Recap
In last lecture, we are left with the open question:
What is the best trade-off between rate and distance?
We called the following example the Hamming Code of length 7 and we saw that it was optimal in that it met the Hamming Bound.

We also came up with a decoding algorithm for this code.
Viewing the code as overlapping circles, we can identify which circles don’t sum to 0 (mod 2) and flip the unique bit that ameliorates the situation.

However, this circle view seems a bit ad hoc.
In this Lecture, we are going to generalize this construction and generalize the decoding algorithm as well as the distance argument.
Linear Algebra over {0, 1}
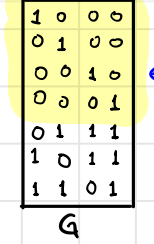
The Hamming code in the previous Example 3 has a really nice form of encoding:

Generator Matrices
We can see this encoding map as the multiplication by a matrix modulo 2, written as $x\mapsto Gx\pmod 2$, where $G$ is some matrix called the Generator Matrix.

Viewing codes generated by a generator matrix is a very useful view to look at things.
For example, the codes in Example 3has a very nice property: it is closed under addition modulo 2, which means that if $c\in \mathcal{C}$, $c’\in \mathcal{C}$, then $c+c’\in \mathcal{C}$.
Writing it as the multiplication by a matrix makes it very clear:

Moreover, we can view any codeword $c\in \mathcal{C}$ as a linear combination of the column vectors of the generator matrix $G$.
In other words, the code $\mathcal{C}$ is the column span of the generator matrix $G$, aka $\mathcal{C}=\text{span}(\text{cols}(G))$ is a linear subspace of dimension 4.
dist (C) = min wt (C)
A key observation is that the minimum Hamming distance of the code is the same as the minimum weight of the non-zero codewords.
Proof:
The proof is straightforward:
$$
\Delta(Gx, Gx’) = \Delta(G(x-x’), 0)=\text{wt}(G(x-x’))
$$
where the first equality holds follows from linearity and $G(x-x’)$ is itself a codeword by the definition. $\blacksquare$
Parity-check Matrices
The other way we looked at Example 3 was placing bits into circles as shown:

Each circle constitutes a parity check, meaning the sum of the circle must equal 0 mod 2. This constrain is indeed the linear relation, which we can express as:

where each of the three rows corresponds to the linear constrains given by a circle. For example, the first row corresponds to the green circle, indicating that $c_2+c_3+c_4+c_5=0 \pmod 2$.
This implies that multiplying any potential codeword by the matrix $H$ should results in 0.
In other words, for any $c\in \mathcal{C}$, we have $Hc=0\pmod2$, which means that $\mathcal{C}$ is contained in the kernel of the matrix $H$:
$$
\mathcal{C}\subseteq \text{Ker}(H)
$$
A raised question is: Does $\mathcal{C}=\text{Ker}(H)?$
The answer is YES!
We prove it by counting dimension.
Proof:
$\text{dim}(\mathcal{C})=\text{dim}(\text{colspan}(G))=4$
It’s easy to see $\text{dim}(\text{colspan}(G))=4$ since the identity matrix is just sitting up there.
$\text{dim}(\text{Ker}(H))=n - \text{rank}(H) = 7 - \text{dim}(\text{rowspan}(H))=4$
Again, it’s easy to see $\text{dim}(\text{rowspan}(H))=3$ because of the identity matrix.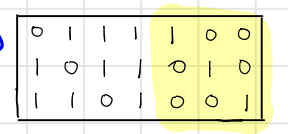
Having $\mathcal{C}\subseteq \text{Ker}(H)$ with the same dimension, $\text{dim}(C)=\text{dim}(\text{Ker}(H))$, it follows that $\mathcal{C}=\text{Ker}(H)$. $\blacksquare$
Informally, the matrix $H$ here is called a Parity-Check matrix of $\mathcal{C}$ so that the code $\mathcal{C}$ is the kernel of this matrix.
Easy to Capture Distance
One benefit of the parity-check matrix is we can read off the distance easily.
As mentioned in the previous lecture, we supposed that the distance of the code in Example 3 is 3. Now, we can provide a proof using parity-check matrices.
Claim: $\text{dist}(\mathcal{C}) = 3$
Proof:
As before, it suffices to show $\min_{c\in \mathcal{C}\backslash\{0, 1\} } \text{wt}(c) = 3$ that the minimum weight of all non-zero codewords is 3.
Firstly, we prove $\text{wt}(c)\ge 3$ for $\forall c\in \mathcal{C}$, meaning that all non-zero codewords has weight of at least 3.
By contradiction, suppose there is some codeword vector $c\in \mathcal{C}$ with has weight 1 or 2 so that $Hc = 0 \pmod 2$.
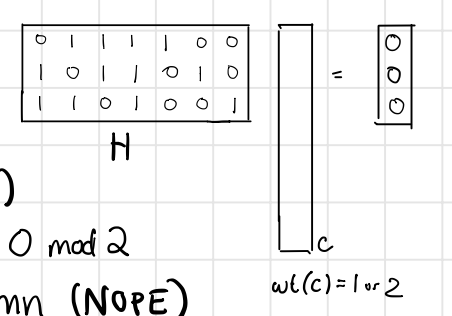
$\text{wt}(c)=1$
It implies one column of $H$ is 0 mod 2. (contradiction)$\text{wt}(c)=2$
It implies the sum of some two columns of $H$ is 0 mod 2, aka there is a repeated column. (contradiction)
Now, the codeword 0101010 has weight exactly 3, so this bound is tight. Hence, the minimum weight is 3. $\blacksquare$
Easy to Decode
Furthermore, the parity-check matrix gives us a slick decoding algorithm.
Recall the puzzle in Example 3:
Puzzle:
Given $\tilde{c}=0111010$, which bit has suffered one bit flip, and what is the original codeword $c$?
The goal of the solution is to find a codeword $c\in \mathcal{C}$ such that the Hamming distance $\Delta(c, \tilde{c})\le 1$.
Solution:
We write $\tilde{c}=c+z\pmod 2$ where $z$ is an error vector with weight 1. Next, we consider what the product of $H\cdot \tilde{c}$ actually is?
One the one hand, compute $H\cdot \tilde{c} \mod 2$ :
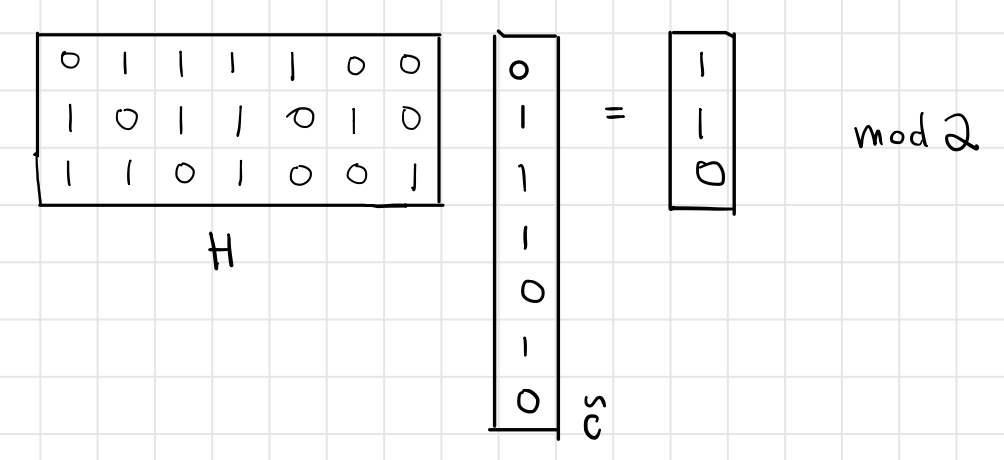
On the other hand, write the product as $H\cdot (c+z) = Hc + Hz =Hz$ since $Hc=0$ for all $c\in \mathcal{C}$.
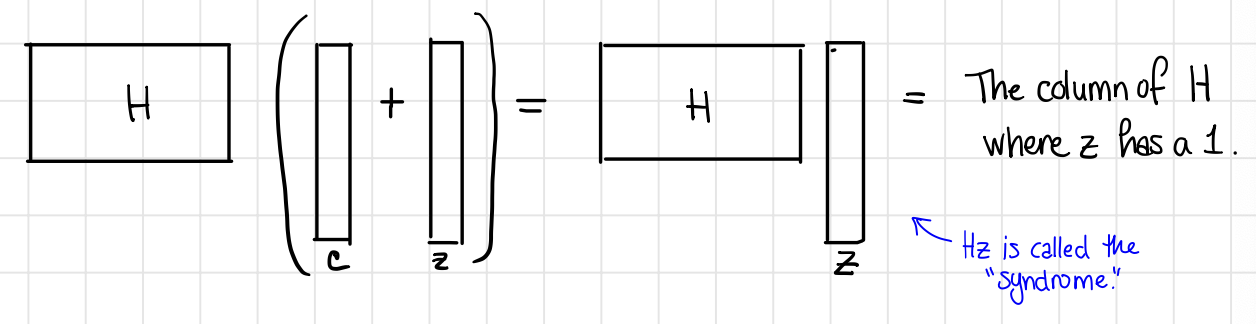
This shows that $z$ is just picking one column of $H$.
From the computation, we see $H\cdot \tilde{c}$ corresponds to the 3rd column of $H$, indicating the error occurred in position 3.
This leads to an efficient decoding algorithm for $\mathcal{C}$:
- Compute $H\cdot \tilde{c}$ and identify which column of $H$ matches the result
- Determine $z$ recover $\tilde{c}=c + z\mod 2$.
This view with parity-check matrix gives us a much nicer way of seeing our circle-based algorithm.
“Which circles fail to sum 1” is the same as “which bits of $H\cdot \tilde{c}$ are 1”, and it picks out which bit we need to flip.
Now, let’s summarize the moral of the story so far:
The Hamming code of length 7 $\mathcal{C}$, is a subspace over $\{0, 1\}^7$, which means we can view it in two different liner-algebraic ways:
- $\mathcal{C}=\{G\cdot x: x\in \{0, 1\}^4\}=\text{span(cols}(G))$, as the column-span of the generator matrix.
- $\mathcal{C}=\{x\in \{0, 1\}^7:H\cdot x=0\} = \text{Ker}(H)$ , as the kernel of the parity-check matrix.
However, all of these are predicated on the assumption that the linear algebra works over $\{0, 1\}$ .
Linear Algebra not Working over {0, 1, 2, 3}
A natural question arises:
Does linear algebra “make sense” over $\{0,1\}$?
To explore this, let’s consider what happens for $\{0, 1,2,3\}$.
Non-example:
Let $G = \left[ \begin{array}{cc} 2 & 0 \\ 0 & 2 \\ 2 & 2 \end{array} \right]$be a generator matrix, mod 4.
Using this generator matrix, we can define a code $\mathcal{C} = \{G\cdot x: x\in \{0, 1, 2,3\}^2\} = \text{colspan}(G)$, with message length $k = 2$, block length $n = 3$, over the alphabet $\Sigma = \{0, 1, 2,3\}$.
Thus, $\text{dim}(\mathcal{C})=2$, since the columns of $G$ are not scalar multiples of each other, aka, they are linearly independent.
Now, consider the parity-check matrix $H = G^{T} = \left[\begin{array}{cc} 2 & 0 & 2 \\ 0 & 2 & 2\\ \end{array} \right]$.
We observe $H\cdot G = 0$, which means $H$ is a legit parity-check matrix for the code $\mathcal{C}$. Specifically, for any $c\in \mathcal{C}$, we have: $H\cdot c = H\cdot G\cdot x = 0 \mod 4$.
However, when we calculate $\text{dim(Ker}(H))$, we find: $\text{dim}(\text{Ker}(H)) = 3 - \text{rank}(H) = 1$.
This leads to a contradiction for the code $\mathcal{C}$ is a liner subspace such that $\mathcal{C} = \text{colspan}(G) = \text{Ker}(H)$.
Additionally, when we look at the distance of code using the parity-check matrix, we find that $\text{dist}(\mathcal{C})\ge 3$ since no two columns of $H$ are linearly dependent.
Yet, there exists a codeword $c = G\cdot \left(\begin{array}{c} 1\\1 \end{array} \right) = \left(\begin{array}{c} 2\\2 \\0 \end{array} \right)$, which has weight $2$, leading to another contradiction.
The main reason for contradiction is that the linear algebra does not “work” over $\{0, 1, 2, 3\} \mod 4$.
In particular, the assertions that two vectors are linearly independent since they are not scalar multiples of each other are not working over $\{0, 1, 2, 3\}$.
The following definitions are both for the linearly independent.
- Non-zero vectors $v$ and $w$ are linearly independent iff there is no non-zero $\lambda$ s.t. $v = \lambda \cdot w$.
- Non-zero vectors $v$ and $w$ are linearly independent iff there is no non-zero $\lambda_1, \lambda_2$ s.t. $\lambda_1 \cdot v + \lambda_2 \cdot w = 0$.
They are the same over the real field $\mathbb{R}$. The proof is straightforward
Proof:
Suppose $\exists \lambda_1, \lambda_2 \ne 0$ s.t. $\lambda_1 \cdot v + \lambda_2 \cdot w = 0$. Then $v = (\frac{-\lambda_2}{\lambda_1})\cdot w$.
Conversely, if $\exists \lambda$ s.t. $v = \lambda w$, then choose $\lambda_2 = \lambda, \lambda_1 = -1$ and $\lambda_1 v + \lambda_2 w = 0$. $\blacksquare$
However, they not the same over $\{0, 1,2, 3\}$. There exists $\lambda_1 =\lambda_2 = 2$ such that
$$ 2\cdot \left(\begin{array}{c} 2 \\ 0 \\2 \end{array}\right ) + 2\cdot \left(\begin{array}{c} 0 \\ 2 \\2 \end{array}\right ) = \left(\begin{array}{c} 4 \\ 4 \\8 \end{array}\right ) = \left(\begin{array}{c} 0 \\ 0 \\0 \end{array}\right ) \mod 4 $$even though the two columns of $G$ are not scalar multiples of each other.
If you have the background of the finite field, the reason here is that $\{0, 1, 2, 3\}$ is not a finite field and we cannot divide by 2 mod 4.
This does not bode well for algebraic coding theory if even linear algebra doesn’t work.
Finite Field and Linear Codes
The key takeaway is all the definitions we know for the linear algebra over $\mathbb{R}$ also make sense over finite fields.
Here, I list some essential points relevant to this lecture.
Let $\mathbb{F}$ be a finite field. Then:
- $\mathbb{F}^n = \{(x_1, \dots, x_n): x_i \in \mathbb{F}\}$
- A subspace $V\subseteq \mathbb{F}^n$ is a subset that is closed unde r addition and scalar multiplication. Specifically: $\forall v, w\in V, \forall \lambda\in \mathbb{F}, v+ \lambda w\in V$.
- Vectors $v_1, \dots, v_t \in \mathbb{F}^n$ are linearly independent if $\forall \lambda_1, \dots, \lambda_t\in \mathbb{F}$ that are not all 0, $\sum_{i} \lambda_i \cdot v_i \ne 0$.
- For $v_1, \dots, v_t \in \mathbb{F}^n$, their span is defined as $\text{span}(v_1, \dots, v_t)=\{\sum_i \lambda_i v_i : \lambda_i \in \mathbb{F}\}$.
- A basis for a subspace $V\subseteq \mathbb{F}$ is a collection of vectors $v_1, \dots, v_t\in V$ s.t.
- $v_1, \dots, v_t$ are linearly independent
- $V = \text{span}(v_1, \dots, v_t)$
- The dimension of a subspace $V$ is the number of elements in any basis of $V$.
Now, we can define a linear code over a finite field.
This definition implies that a linear code is essentially a linear space.
This definition aligns with the one we introduced in the previous lecture.
Here, we use overloaded $k$ for both message length and dimension. This is intentional, as it makes sense in this context.
If $\mathcal{C}$ is a $k$-dimensional subspace over $\mathbb{F}$, then $|\mathcal{C}|=|\mathbb{F}^k|$, hence $k = \log _{|\mathbb{F}|}|\mathcal{C}| = \log_{|\Sigma|}|\mathcal{C}|=$ message length.
Moreover, if $\mathcal{C}$ is a code of block length $n$, message length $k$, over alphabet $\mathcal{\Sigma = \mathbb{F}}$, then $\mathcal{C}$ is a linear code and also a $k$-dimensional subspace over $\mathbb{F}$.
Observation:
Any linear code has a generator matrix.
Proof:
Choose the columns of $G$ to be a basis of $\mathcal{C}$. $\blacksquare$
Note that the generator matrix for a code is not unique. There can be many generator matrices for the same code. They all describe the same code, but they implicitly describe different encoding maps.
For example, the following $G$ and $G’$ are both generator matrices for the same Hamming code.
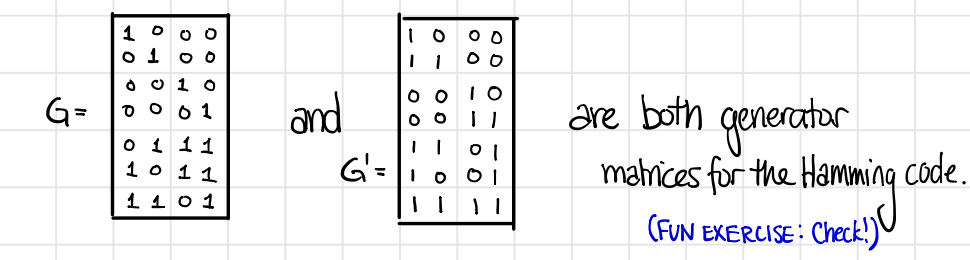
In particular, we can always permute on rows since it does not change the space of column-span.
Some generator matrices may be more useful than others. For example, $G$ above corresponds to a systematic encoding map. This means that that $\text{Enc}_G(x_1, x_2, x_3, x_4) \mapsto (x_1, x_2, x_3, x_4, \text{stuff})$.
In particular, for linear codes, there is always a systematic encoding map defined by a generator matrix look like the above $G$, having an identity matrix sit up there and some other stuff down there.
Observation:
Any linear code has a parity-check matrix.
Proof:
Choose the rows of $H$ to be a basis of $\mathcal{C}^\perp$. $\blacksquare$
Similarly, the parity-check matrix for a code is not unique—there can be many parity-check matrices for the same code.
With these definitions under our belts, we can move to some facts about linear codes.
Facts About Linear Codes:
If $\mathcal{C}\subseteq \mathbb{F}^n$ is a linear code over $\mathbb{F}$ of dimension $k$ with the generator matrix $G$ and parity-check matrix $H$, then:
- $H\cdot G = 0$
- $\mathcal{C}^\perp$ is a linear code of dimension $n-k$ with generator matrix $H^T$ and parity-check matrix $G^T$.
Note that the parity-check matrix $H$ for code $\mathcal{C}$ is taken as the generator matrix for $\mathcal{C}^\perp$. - The distance of $\mathcal{C}$ is the minimum weight of any nonzero codeword in $\mathcal{C}$: $\text{dist}(\mathcal{C})=\min_{c\in \mathcal{C}\backslash\{0\}}\sum_{i=0}1\{c_i \ne 0\}$.
- The distance of $\mathcal{C}$ is the smallest number $d$ so that $H$ has $d$ linearly dependent columns.
Recall how we proved the distance of the code in Example 3: we argue that it suffices to show that no pairs of columns in $H$ are linearly dependent.
As shown below, the distance of the code corresponds to the smallest number $d$ so that there exists a codeword $c$ of weight $d$, which is picking up $d$ columns of $H$ that is linearly dependent.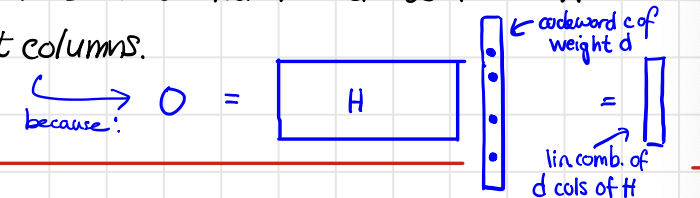
「Algebraic ECCs」: Lec2 Linear Codes and Finite Fields

