「Algebraic ECCs」: Lec3 GV Bound and q-ARY Entropy

In this series, I will be learning Algebraic Error Correcting Codes, lectured by Mary Wootters. The lecture videos are available here. Feedback and sugguestions are always welcome! ^ - ^

Topics Covered:

• The GV Bound:
• Efficiency and Maximum-Likelihood Decoding
• Application: McEliece Cryptosystem
• Off to Asymptopia
  • Family of Codes
  • q-ary Entropy
  • Trade-off Between Rate and Distance

Recap

In the last lecture, we saw linear codes over a finite field in two linear-algebraic ways. As figured below, we can view a code as the column-span of a generator matrix and as the kernel of the parity-check matrix. There can be many different generator matrices and parity-check matrices for the same code.

Today, we are going to learn some useful things one can do with linear codes.

The GV Bound

In Lecture 2, we explored the Hamming bound:

$$
R\le 1 - \frac{\log_q\text{Vol}_q(\lfloor \frac{d-1}{2}\rfloor, n)}{n}
$$

which provides an upper bound on the rate of code. This bound highlights an impossible result, meaning that we cannot construct a code with a large rate.

In contrast, the Gilbert-Varshamov (GV) bound offers a possible result. It demonstrates that there exist codes with a decent rate.

Gilber-Varshamov (GV) Bound:

For any prime power $q$, and for any $d\le n$, there exists a linear code $\mathcal{C}$ of length $n$, alphabet size $q$, distance $d$, and rate $$ R\ge 1 - \frac{\log_q {(\text{Vol}_q(d-1, n))-1}}{n} $$ Note: you can remove the words “prime power” and “linear” and the statements is till true.

Aside from the fact that the GV bound provides a possibility result, another difference lies in the quantity difference in the $q$-ary volume of the Hamming ball.

We’ll explore the relationship between these two bounds later, but for now, keep in mind that the rate given by the GV bound must be less than that of the Hamming bound:

$$
R_{\text{GV}} < R_{\text{Hamming}}
$$

otherwise, the math is broken.

Now, we’ll prove the GV bound — it’s pretty easy!

Proof of the GV Bound:

• The idea of the proof is to choose a random linear code $\mathcal{C}$ of specific dimension $k$, and show that it has a distance at least $d$ with non-zero probability—that is:

$$
\text{Pr}[\mathcal{C} \text{ has distance}\ge d]>0
$$

​ This implies that there exists a linear code with a decent rate.

This approach is known as the Probabilisitic Method.

• Let $\mathcal{C}$ be a random subspace of $\mathbb{F}_q^n$ with dimension $k = n -\log_q(\text{Vol}_q(d-1, n))-1$.
  If this code achieves a good distance, the $k/n$ basically corresponds to the rate given in the GV bound.
  This construction works because a linear code is essentially a linear space. Since there are finitely many subspaces of dimension $k$ in $\mathbb{F}_q^n$, we can uniformly sample a random linear subspace.

• Let $G\in \mathbb{F}_q^{n\times k}$ be a random generator matrix for $\mathcal{C}$.
  As discussed before, each code can have many generator matrices. We can uniformly sample one by selecting a random basis for the subspace and using it as the columns of the generator matrix.

• Now, since the distance is the minimum weight of all non-zero codewords in the linear code, we have $\text{dist}(\mathcal{C})=\min_{c\in \mathcal{C}\backslash{0}}\text{wt}(c)=\min_{x\in \mathbb{F}_q^k\backslash{0}}\text{wt}(G\cdot x)$.

• Useful Fact:
  For any fixed $x\ne 0$, $G\cdot x$ is uniformly random in $\mathbb{F}_q^n\backslash{0}$.

• For any given $x\ne 0$, using the useful fact, the probability that the weight of $G\cdot x$ is less than $d$ is equal to the probability of a random non-zero codeword lying within the Hamming ball centered at 0 with radius $d-1$. It is basically the volume of the Hamming ball divided by the volume of the whole space as indicated in the following second equality.

$$
\begin{aligned}
\text{Pr}_G{\text{wt}(G\cdot x)<d} &= \text{Pr}_G{G\cdot x\in B_q(0, d-1)}\
&= \frac{\text{Vol}_q(d-1, n)-1}{q^n-1}\
&\le \frac{\text{Vol}_q(d-1, n)}{q^n}
\end{aligned}
$$

• By the union bound, we have

$$
\text{Pr}{\exists x\in \mathbb{F}_q^k:\text{wt}(G\cdot x)<d}\le q^k\cdot \frac{\text{Vol}_q(d-1, n)}{q^n}
$$

• The complement of this event is that $\forall x\in \mathbb{F}_q^k$ , $\text{wt}(G\cdot x)\ge d$, which implies that the distance of the code is at least $d$.

• Thus, we win as long as this probability is strictly less than $1$, which guarantees the existence of a code with a good distance with non-zero probability.

• Taking logs of both sides, we win if

$$
k-n+\log_q(\text{Vol}_q(d-1, n))<0
$$

• This is true since we precisely choose $k = n-\log_q(\text{Vol}_q(d-1, n))-1$ before. $\blacksquare$

Efficiency & Maximum-Likelihood Decoding

The GV bound tells us there exists good codes with decent rates.

Next, we are going to discuss the extent to which linear codes admit efficient algorithms.

We have the following efficient algorithms for linear codes to encode, detect errors and correct erasures:

• Efficient Encoding:
  If $\mathcal{C}$ is linear, we have an efficient encoding map $x\mapsto G\cdot x$.
  The computational cost is one matrix-vector multiplication.

• Efficient Error Detection:
  If $\mathcal{C}$ is linear with distance $d$, we can detect $\le d - 1$ errors efficiently:
  If $0< \text{wt}(e)\le d-1$ and $c\in \mathcal{C}$, then $H(c+e)=H\cdot e \ne 0$. Thus, we can just simply check if $H\tilde{c}=0$.

• Efficient Erasure Correction:
  If $\mathcal{C}$ is linear with distance $d$, we can correct $\le d-1$ erasures efficiently:
  Erasing bits in the codeword $c$ corresponds to removing the corresponding rows of the generator matrix $G$.

  

  The remaining $n-(d-1)$ rows form a new linear system $G’\cdot x = c’$. Since we know a code with distance $d$ can handle up to $d-1$ erasures (albeit with a non-efficient algorithm), there must be exactly one $x$ that is consistent with this linear system, and hence $G’$is full rank. The remaining task is to solve this linear system, which can be done with Gaussian elimination.

  

The above is leaving out one important thing—correcting errors.

We know how to correct errors in the $(7, 4, 3)_2$-Hamming code, but what about in general?

If $\mathcal{C}$ is linear with distance $d$, can we correct up to $\lfloor \frac{d-1}{2} \rfloor$ errors efficiently?

The bad news is no.

Consider the following problem. If we would solve this problem, we can correct up to $\lfloor \frac{d-1}{2} \rfloor$ errors.

Maximum-Likelihood Decoding for Linear Codes:

Given $\tilde{c}\in \mathbb{F}_q^n$, and $G\in \mathbb{F}_q^{n\times k}$, find $x\in \mathbb{F}_q^k$ such that $\Delta(G\cdot x, \tilde{c})$ is minimized. Aka, find the codeword closest to a received word $\tilde{c}$.

This problem (called Maximum-likelihood decoding for linear codes) is NP-hard in general [Berlekamp-McEliece-Van Tilborg 1978], even if the code is known in advance and you have an arbitrary amount of preprocessing time [Bruck-Noar 1990, Lobstein 1990]. It is even NP-hard to approximate (within a constant factor)! [Arora-Babai-Stern-Sweedyk 1993].

Even computing the minimum distance of linear codes is NP-hard given the generator matrix.

The take-away here is that we are unlikely to find a polynomial-time algorithm for this task. This may sounds discouraging, but remember that NP-hardness is a worst-case condition. While there exist linear codes that are probably hard to decode, but this does not imply that that all of them are.

Going forward, we will focus on designing codes that admit efficiently-decodable algorithms. Before that, let’s look at a cryptography application that leverages this decoding hardness.

Application: McEliece Cryptosystem

McEliece cryptosystem is a public-key scheme based on the decoding hardness of binary linear codes.

Suppose that Alice and Bob want to talk securely. Now there is no noise, just an Eavesdropper Eve.

In public key cryptography, everyone has a public key and a private key. To send a message to Bob, Alice encrypts it using Bob’s public key. Bob decodes it with his private key. We hope this process is secure as long as Bob’s private key stays private.

The McEliece Cryptosystem consists of three main algorithms:

• Generate Private and Public Keys

  1. Bob chooses $G\in \mathbb{F}_2^{n\times k}$, the generator matrix for an (appropriate) binaray linear code $\mathcal{C}$ that is efficiently decodable from $t$ errors.

     Not all codes work for McEliece crytosystem; the chosen code at least must be efficiently decodable. In particular, McEliece cryptosystem uses a binary “Goppa Code”.

  2. Bob chooses a random invertible $S\in \mathbb{F}_2^{k\times k}$ and a random permutation matrix $P\in \mathbb{F}_2^{n\times n}$. The permutation matrix $P$ has exactly one 1 in each column such that $Px$ permutes the coordinates of the vector $x$.

  3. Bob’s private key is $(S, G, P)$.

  4. Bob’s public key consists of $\hat{G}=PGS$ and the parameter $t$.

• Encrypt with Bob’s Public key
  To send a message $x\in \mathbb{F}_2^k$ to Bob:

  1. Alice chooses a random vector $e\in \mathbb{F}_2^n$ with $\text{wt}(e)=t$.
  2. Alice sends $\hat{G}x+e$ to Bob.

• Decrypt with Bob’s Private Key
  To decrypt the message $G’x+e$:

  1. Bob computes $P^{-1}(\hat{G}x+e)=GSx + P^{-1} e =G(Sx) +e’$, where $\text{wt}(e’)=t$.

     At this point, we write it as a corrupted codeword $G(Sx)+e’$ with exactly $t$ errors since the permutation matrix $P^{-1}$ only permutes the coordinates of $e$. Bob can use the fact that $G$ is the generator matrix for a code that is efficiently able to correct up to $t$ errors.

  2. Bob uses the efficient decoding algorithm to recover $Sx$.

  3. Bob can compute $x = S^{-1}\cdot Sx$.

Why might this be secure?

Suppose Eve sees $\hat{G}x+e$ and she knows $G’$ and $t$. Hence, this problem is the same as decoding the code $\hat{C}={\hat{G}x : x\in \mathbb{F}_2^k}$ from $t$ errors.

The security of the McEliece crytosystem relies the following assumptions:

1. The public key $\hat{G}$ looks random: By scrambling $G$ with $S$ and $P$, it is difficult for Eve to distinguish $\hat{G}$ from a random generator matrix.
2. Decoding a random linear code is computationally hard: While decoding the worst-case code is NP-hard, it is not too much of stretch that decoding a random linear code is also hard on average.

If these assumptions hold true, decoding the code $\hat{C}={\hat{G}x : x\in \mathbb{F}_2^k}$ from $t$ errors is computationally hard for Eve.

This assumption that “Decoding $\hat{G}x+e$ is hard” (for an appropriate choice of $G$) is called the McEliece Assumption. Some people believe it and some don’t.

“Decoding $\hat{G}x+e$ is hard for Eve” is NOT the same as “Maximum likelihood decoding of linear codes is NP-hard”.
There are two main differences:
First, we have some promise that there were $\le t$ errors in McEliece assumption.
Second, NP-harness is a worst-case assumption. For cryptography, we need an average-case assumption.

Worst-case vs. Average-case:
Worst-case: The problem is considered hard on worst-case if it is difficult to solve for the most difficult case. If a solution is found for the worst-case instance, the problem is solvable for all instances, e.g. $P\ne NP$.

Average-case: The problem is considered hard if it is difficult to solve for a randomly chosen instance. This assumes that solving the problem is computationally hard for the “average” case rather than just the hardest instance.

In cryptography, average-case hardness is more relevant because security relies on the assumption that attackers cannot efficiently solve a typical random instance of the underlying problem (e.g., decoding a random linear code or factoring a randomly chosen large integer).

Off to Asymptopia

So far, we’ve seen the optimal rate for a code with distance $d$ and $|\Sigma|=q$ is bounded above by the Hamming bound and bounded below by the GV bound.

$$
1-\frac{1}{n}\cdot \log_q (\text{Vol}_q(d-1, n))\le k/n \le 1 - \frac{1}{n} \cdot \log_q(\text{Vol}_q(\left\lfloor \frac{d-1}{2}\right \rfloor, n)
$$

Recall the combinational question we posed in Lecture 1:

What is the best trade-off between rate and distance?

To address this in the asymptotical setting, we are going to think about the following limiting parameter regime: $n, k, d\rightarrow \infty$ so that the rate $k/n$ and the relative distance $\delta$ approaches constants.

The motivations for this parameter regime:

1. It will allow us to better understand what’s possible and what’s not.
2. In many applications, $n, k, d$ are pretty large and $R, \delta$ are the things we want to be thinking about.
3. It will let us talk meaningfully about computational complexity.

Family of Codes

Before that, let’s define a family of codes.

A Family of Codes

A family of codes is a collection $\mathcal{C}=\{\mathcal{C}_i\}_{i=1}^{\infty}$, where $\mathcal{C}_i$ is an $(n_i, k_i, d_i)_{q_i}$ code. Given such a family of codes, we can define the rate and the relative distance: The rate of $\mathcal{C}$ is $R(\mathcal{C})=\lim_{i\to \infty} k_i/n_i$. The relative distance of $\mathcal{C}$ is $\delta{(\mathcal{C}})=\lim_{i\to \infty} d_i /n_i$.

We will frequently abuse notation and refer to $\mathcal{C}$ as a “code”, and we’ll drop the subscript $i$ and just think about $n, k, d\to \infty$

Now, let’s look at an example of a family of codes—Hamming codes.

The $i$-th code $\mathcal{C}_i$ is a $(2^i-1, 2^i-i-1, 3)_2$ code so $\mathcal{C}=\{\mathcal{C}_i\}_{i=1}^\infty$ represents a family of codes. $\mathcal{C}_i$ is defined by its parity-check matrix, where the columns corresponds to the binary vector representations of all non-zero elements of $\mathbb{F}_{2^i}$.

The rate of this family is:

$$
\lim_{i\to \infty }\frac{2^i-i-1}{2^i-1}=1
$$

This rate approaches to 1, which is a very good rate.

However, the relative distance is:

$$
\lim_{i\to \infty}\frac{3}{2^i-1}=0
$$

Hence, in the asymptotic setting, our question is: for any family of a code,

What is the best trade-off between $R(\mathcal{C})$ and $\delta{(\mathcal{C})}$?

As we see in the family of Hamming codes, we cannot achieve good trade-off between rate and distance. While it has a phenomenal rate, its distance is poor.

An easier question to ask is:

Can we obtain codes with $R(\mathcal{C})>0$ and $\delta{(\mathcal{C})}>0$?

We define a family of codes with the rate $R(\mathcal{C})>0$ and relative distance $\delta(\mathcal{C})>0$ (both strictly greater than 0) as asymptotically good.

q-ary Entropy

Now we have an asymptotic parameter regime, how should we parse the GV and Hamming bounds? In particular, what do these bounds look like in terms of $\delta$?

$$
1-\frac{1}{n}\cdot \log_q (\text{Vol}_q(d-1, n))\le R(\mathcal{C}) \le 1 - \frac{1}{n} \cdot \log_q(\text{Vol}_q(\left\lfloor \frac{d-1}{2}\right \rfloor, n)
$$

We know that $\text{Vol}_q(\lfloor \frac{d-1}{2} \rfloor, n)=\sum_{j=0}^{\lfloor {d-1\over 2}\rfloor}{n\choose j}(q-1)^j$ but this expression is not very helpful for analysis.

To address this, we use the $q$-ary entropy function, which provides a concise way to capture the volume of Hamming balls.

q-ary Entropy Function:

The q-ary entropy function $H_q:[0,1]\to [0, 1]$ is defined as: $$ H_q(x)=x\log_q(q-1)-x\log_q(x)-(1-x)\log_q(1-x) $$ This generalizes the binary entropy function $H_2(x)=-x\log x - (1-x)\log (1-x)$.

Using q-ary entropy function, we can bound the volume of the Hamming ball with the following propositions, allowing us to replace the pesky volume expression with cleaner approximations.

Propositions:

Let $q\ge 2$ be an integer, and let $0\le p \le 1 - {1\over q}$. Then:

• $\text{Vol}_q(pn, n)\le q^{n\cdot H_q(p)}$
• $\text{Vol}_q(pn, n)\ge q^{n\cdot H_q(p) - o(n)}$

Here, the $o(n)$ term is a function $f(n)$ such that $\lim_{n\to \infty}{f(n)\over n}\to 0$. We can consider this term as negligible compared to $n\cdot H_q(p)$.

Intuitive Interpretation of q-ary entropy:
The binary entropy function $H_2(p)$ is often described in terms of the number of bits needed to describe something. For example, a random string of length $n$, where each bit is 1 with probability $p$, can be described using $n\cdot H_2(p)$ bits.

There is a similar interpretation for $q$-ary entropy. Suppose we choose $x\in \mathbb{F}_q^n$ s.t. each $x_i$ is 0 with probability $1-p$ and random in $\mathbb{F}_q^*$ with probability $p$. $$ x_i=\begin{cases}0 &\text{w/ prob. }1-p\\\text{random in }\mathbb{F}_q^* &\text{w/ prob. }p\end{cases} $$
Then, the number of bits needed to describe $x$ is roughly $n\cdot H_2(p)$.

Before proceeding, let’s examine how this q-ary entropy function behaves.

• $H_2(x)$: This function is 0 at $x=0$ and $x=1$, with a maximum value of $1$ at $x={1\over 2}$.
• $H_3(x)$: It resembles $H_2(x)$ but is slightly shoved over to the right. It’s maximum value occurs at $x={2\over 3}$.
• $H_6(x)$: This function is shifted further to the right, with its maximum value occurring at $x=\frac{5}{6}$.
• More generally, $H_q(x)$ has the maximum value of $1$ at $x={q-1\over q}$. As $q$ increases, curve of the function is shoved more and more over to the right.

Here are some useful properties of $H_q(x)$:

• If $p\in [0, 1]$ is constant and $q\to \infty$, then

  $$ H_q(p)= \underbrace{p\cdot \log_q(q-1)}_{\text{basically 1}}+\underbrace{O(\log_q(\text{stuff}))}_{\text{really small}}\approx p $$

  So, eventually the plot looks like a line of $H_q(p)=p$ and a little hicky at the end.

  

• If $q$ is constant and $p\to 0$, then

  $$ \begin{align} H_q(p)&=\underbrace{p\cdot \log_q(q-1)}_{O(p)}+\underbrace{p\log_q\left({1\over p}\right)}_{\text{This term is the largest}}+ \underbrace{(1-p)\log_q\left({1\over 1-p}\right )}_{\approx p/\ln(q) =O(p)}\\ &\approx p\log_q\left({1\over p}\right) \end{align} $$

  So, near the origin, all those curves look like $x\ln(1/x)\over \ln q$.

The following is my own analysis for the last term $(1-p)\cdot \log_q\left ({1\over 1-p}\right)$ using Taylor expansion.

Analyze the last term using Taylor expansions:

• The Taylor expansion of $f(x)$ at $x=a$ is

  $$
  \begin{align}
  f(x)&=\sum_{n = 0}^\infty\frac{f^{(n)}(a)}{n!}(x-a)^n \
  &=f(a)+f’(a)\cdot (x-a)+\frac{f’’(a)}{2!}\cdot (x-a)^2+\dots
  \end{align}
  $$

• Derivatives of $\ln (x)$ are given as: $\ln’(x)=x^{-1}$, $\ln^{‘’}(x)=(-1)\cdot x^{-2}$, $\ln^{(3)}=(-1)\cdot (-2)\cdot x^{-3}$. By deduction, we have: $\ln^{(n)}(x)=(-1)^{n-1}\cdot (n-1)!\cdot x^{-n}$.

• The Taylor expansion of $\ln(x)$ at $x=1$ is:

  $$
  \begin{align}
  \ln(x) &= \ln(1)+\sum_{n=1}^{\infty} \frac{\ln^{n}(1)}{n!}\cdot (x-1)^n\&=\sum_{n=1}^{\infty}(-1)^{n-1}\cdot {1\over n}\cdot (x-1)^n\
  &=(x-1) -{(x-1)^2\over 2}+{(x-1)^3\over 3}-\dots+{(-1)^{n-1}\over n}\cdot (x-1)^n
  \end{align}
  $$

• Applying this expansion to the last term:

  $$
  \begin{align}
  \log_q\left ({1\over 1-p}\right)&=-{\ln (1-p) \over \ln q}\
  &=-{1\over \ln q}\cdot [(-p)-\frac{(-p)^2}{2}+\dots]\
  &\approx {1\over \ln q}\cdot p
  \end{align}
  $$

• This shows that $\lim_{p\to 0}(1-p)\cdot \log_q\left ({1\over 1-p}\right)\approx p/\ln (q)=O(p)$

---

Now, we can use them to simplify our expression for GV and Hamming bounds, both involving the the volume of the q-ary Hamming ball. The strategy is to take log base $q$ of the following approximation in terms of the $\delta$:

$$
\text{Vol}_q(\delta n, n)\approx q^{n\cdot H_q(\delta)}
$$

We can replace the pesky term $\log_q \text{Vol}_q(\delta n,n)$ with $n\cdot H_q(\delta)$.

Hamming Bound:

For any family $\mathcal{C}$ of the q-ary codes, we have $$ R(\mathcal{C})\le 1 - H_q(\delta{\mathcal{(C)}}/2) $$

GV Bound:

GV Bound:

Let $q\ge 2$. For any $0\le \delta\le 1- \frac{1}{q}$, and for any $0< \epsilon \le 1 - H_q(\delta)$, there exists a q-ary family of codes $\mathcal{C}$ with $\delta(\mathcal{C})\ge \delta$ and $$ R(\mathcal{C})\ge 1 - H_q(\delta)-\epsilon $$

Trade-off Between Rate and Distance

Now, it’s easier to compare these two bounds:

The following plot the trade-off for $q=2$ in terms of only the rate $R$ and the relative distance $\delta$, without considering $n, k, d$.

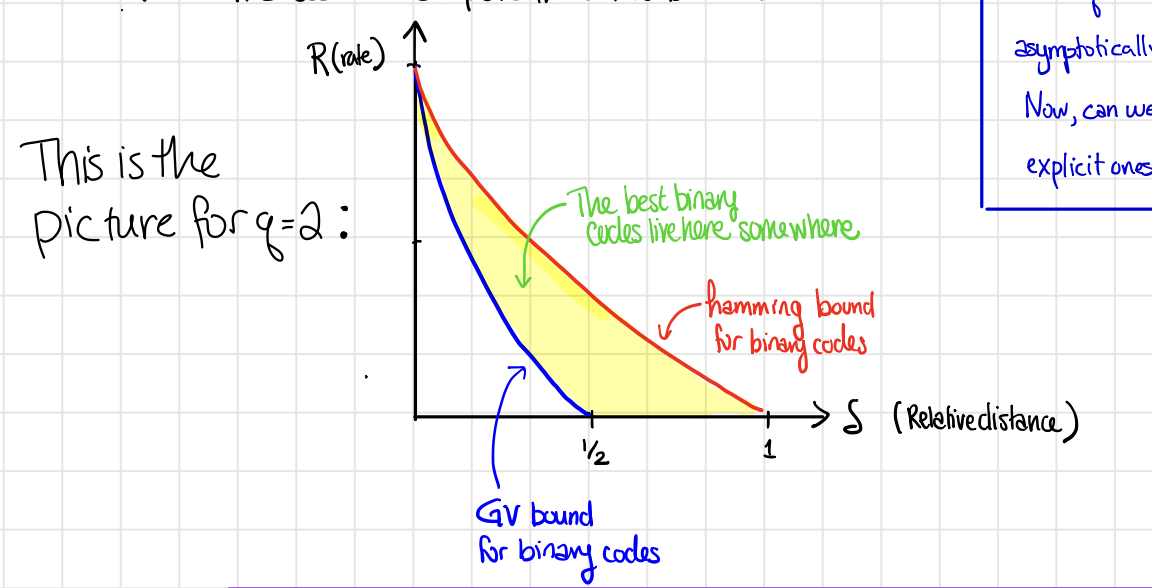
• The red line represents the Hamming bound for binary codes.
  Notably, no point above the Hamming bound is achievable by any binary codes.
• The blue line represents the GV bound for binary codes.
  Notably, any point below the GV bound is achievable by some codes.
• The yellow region is an area of uncertainty.
• We would like to push the GV bound as much up as possible while at the same time try and push down the Hamming bound as much as possible.

Note that the GV bound answers our earlier question:

There do exist asymptotic good codes!

But, can we find some explicit ones with efficient algorithms?

Regarding the yellow uncertain region, there are several other interesting questions:

• Are there family of codes that beat the GV bound?
  The answer is both yes and no.
  • Answer 1: Yes. For $q=49$, “Algebraic Geometry Codes” beat the GV bound.
  • Answer 2: For binary codes, we don’t know.
    This remains an OPEN QUESTION! The GV bound (which is relatively straighforward to prove) is the best-known possibility of result we have for binary codes.
• Can we find explicit constructions of families of codes that meet the GV bound?
  Recall that our proof for GV bound is non-constructive; it uses the probabilistic method to show the existence of a random linear codes with decent rates. However, we are looking for explicit descriptions or efficient algorithms to construct such codes.
  • Answer 1: Yes, for large alphabet. (We’ll see soon)
  • Answer 2: For binary codes, recent work [Ta-Shma 2017] gives something close in a very particular parameter regime…but in general, it’s still an OPEN QUESTION!