「机器学习-李宏毅」:Error
这篇文章叙述了进行regression时,where dose the error come from?
这篇文章除了解释了error为什么来自bias和variance,还给出了当error产生时应该怎么办?如何让模型在实践应用中也能表现地和测试时几乎一样的好?
Error
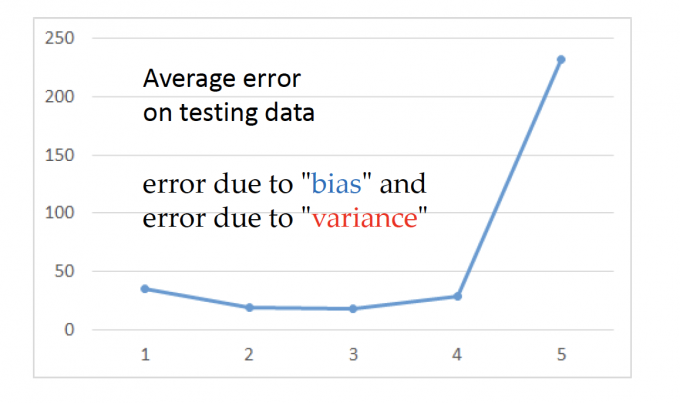
在中的2.4节,我们比较了不同的Model。下图为不同Model下,testing data error的变化。
可以发现,随着模型越来越复杂,testing data的error变小一些后,爆炸增大。
越复杂的模型在testing data上不一定能得到好的performance。
所以,where dose the error come from?
:bias and variance
Bias and Variance of Estimator
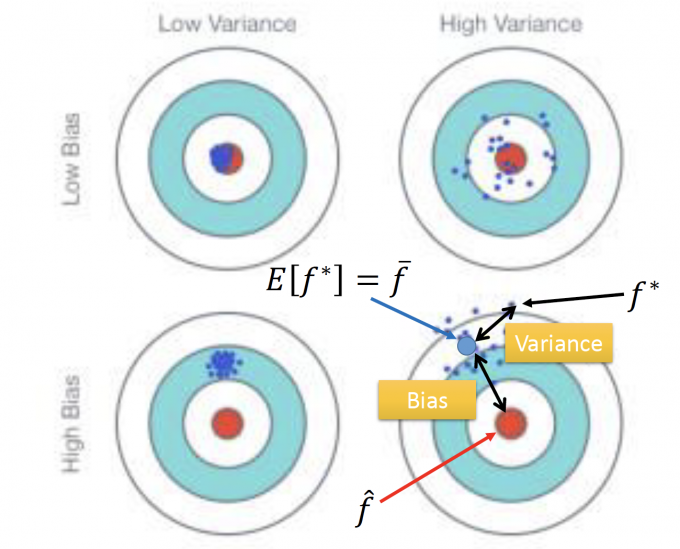
用打靶作比,如果你的准心,没有对准靶心,那打出的很多发子弹的中心应该离靶心有一段距离,这就是bias。
但把准心对准靶心,你也不一定能打中靶心,可能会有风速等一系列原因,让子弹落在靶心周围,这就是variance。
上图中,可以直观体现出bias 和 variance的影响。
概率论中 :
一个通过样本值得到了估计量,有三个评判准则:无偏性、有效性和相和性。
这里的无偏性的偏也就是bias。
概率论中定义:设 $\hat{\theta}(X_1,X_2,…,X_n)$ 是未知参数 $\theta$ 的估计量,若 $E(\hat{\theta})=\theta$ ,则称 $\hat{\theta}$ 是 $\theta$ 的无偏估计。
变量 $x$ ,假设他的期望是 $\mu$ ,他的方差是 $\sigma^2$.
对于样本: $x^1,x^2,…,x^N$ ,估计他的期望和方差。
概率论的知识: $m=\frac{1}{N} \sum_{n} x^{n} \quad s^{2}=\frac{1}{N} \sum_{n}\left(x^{n}-m\right)^{2}$
$E(m)=\mu$ ,所以用 $m$ 是 $\mu$ 的无偏估计。(unbiased)
但是 $E\left[s^{2}\right]=\frac{N-1}{N} \sigma^{2} \quad \neq \sigma^{2}$ ,所以这样的估计是有偏差的。(biased)
因此统计学中用样本估算总体方差都进行了修正。
而在机器学习中,Bias和Variance通常与模型相关。
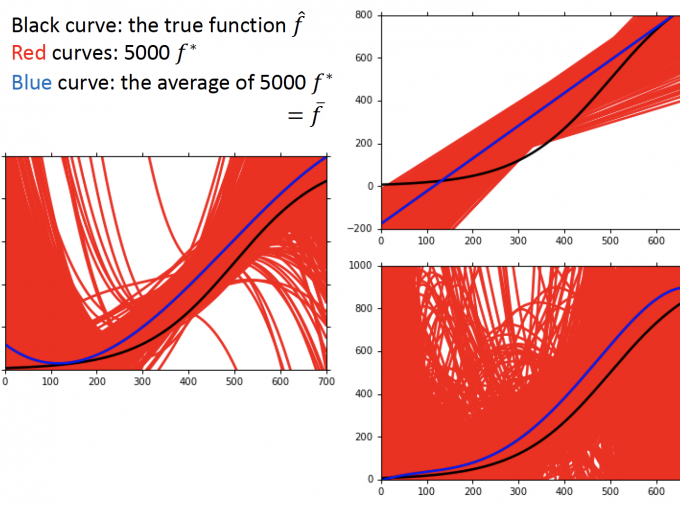
上图中,假设黑色的线是 true function,红色的线是训练得到的函数,蓝色的线是,训练函数的平均函数。
可见,随着函数模型越来越复杂,bias在变小,但variance也在增大。
右下角图中,红色的线接近铺满了,variance已经很大了,模型过拟合了。
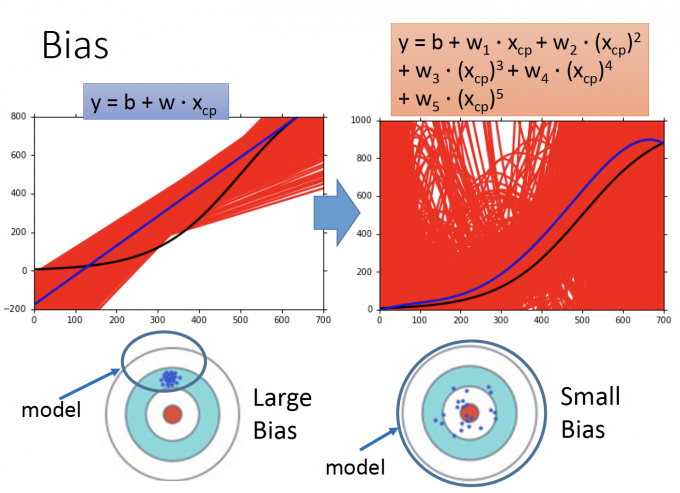
对机器学习中模型对bias影响的直观解释
左图的model简单,右图的model复杂。
简单的model,包含的函数集较小,可能集合圈根本没有包括target(true function),因此在这个model下,无论怎么训练,得到的函数都有 large bias。
而右图中,因为函数非常复杂,所以大概率包含了target,因此训练出的函数可能variacne很大,但有 small bias。
what to do with large bias/variance
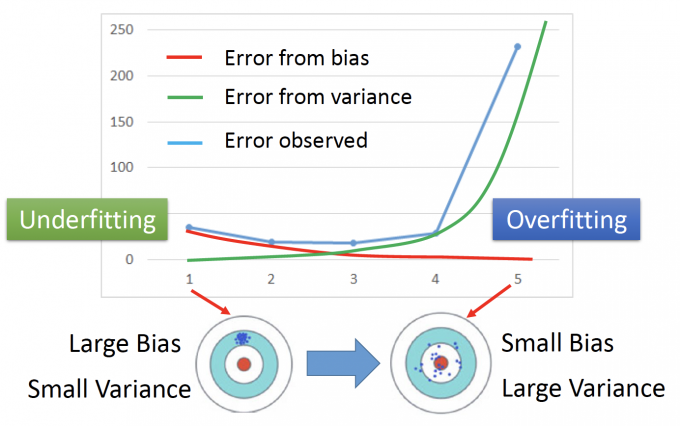
上图中,红色的线表示bias的误差,绿色的线表示variance的误差,蓝色的线表示观测的误差。
当模型过于简单时:来自bias的误差会较大,来自vaiance的误差较小,也就是 Large Bias Small Variance
当模型过雨复杂时:来自bias的误差会较小,来自variance的误差会很大,也就是 Small Bias Large Variance
2 case :
- Underfitting :If your model cannot even fit the training examples, then you have large bias.
- Overfitting : If you can fit the traning data, but large error on testing data , then you probably have large variance.
With Large Bias
For bias, redesign your model.
- Add more features as input.
- A more complex model.
考虑更多的feature;使用稍微复杂些的模型。
With Large Variance
- More data
- Regularization (在这篇2.5.2文章中有叙述什么是regularization)
Model Selection
- There is usually a trade-off beween bias and variance.
- Select a model that balances two kinds of error to minimize total error.
选择模型需要在bias和variance中平衡,尽量使得总error最小。
What you should NOT do:
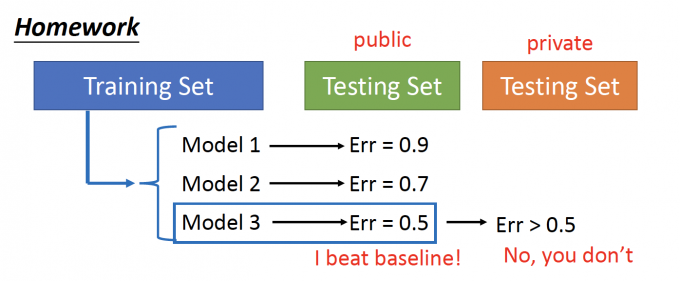
以上,描述的是这样的一个情形:在traning data中,得到了三个自认不错的模型,kaggle的公开的testing data测试,分别得到三个模型的error,认为第三个模型最好!
但是,当把kaggle用private的testing data 进行测试时,error肯定是大于0.5的,最好的model也不一定是第三个。
同理,当把我们训练出的model拿来实际应用时,可能会发现情况很糟,并且,这个model可能选的是测试中最好的,但在应用中并不是最好的。
Cross Validation
什么是Cross Validation(交叉验证)?
在机器学习中,就是下图过程:
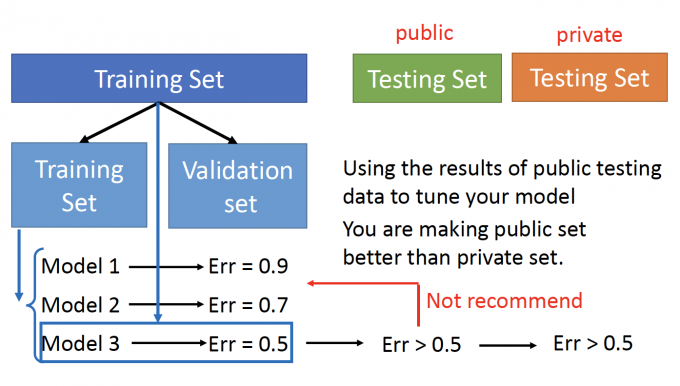
把Traning Set 分成两个部分:Training Set和Validation Set。
在Training Set部分选出模型。
用Validation Set来判断哪个模型好:计算模型在Validate Set的error。
再用模型预测Testing Set(public),得到的error一定是比Validation Set中大的。
Not recommend :
Not用public testing data的误差结果去调整你的模型。
这样会让模型在public的performance比private的好。
但模型在private testing data的performance才是我们真正关注的。
那么当模型预测private testing set时(投入应用时),能尽最大可能的保证模型和在预测public testing data相近。
N-fold Cross Validation
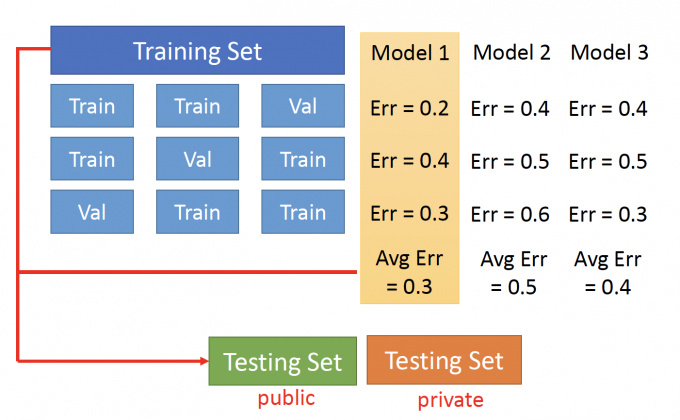
N-fold Cross Validation(N-折交叉验证)的过程如下:
- 把Training Set 分为3(3-fold)份,每一次拿其中一份当Validation Set,另外两份当作Training Set。
- 每一次用Train Set来训练。得到了三个Model。
- 要判断哪一个Model好?
- 每一个Model都计算出不同Validation Set的error。
- 得到一个Average Error。
- 最后选这个average error最小的model。
- 最后应用在public traning set,来评估模型应用在private training set的performance。
「机器学习-李宏毅」:Error