「机器学习-李宏毅」:Classification-Probabilistic Generative Model
Classification 有Generative Model和Discriminative Model。
这篇文章主要讲述了用生成模型来做分类的原理及过程。
What is Classification?
分类是什么呢?分类可以应用到哪些场景呢?
Credit Scoring【贷款评估】
Input: income, savings, profession, age, past financial history ……
Output: accept or refuse
Medical Diagnosis【医疗诊断】
Input: current symptoms, age, gender, past medical history ……
Output: which kind of diseases
Handwritten character recognition【手写数字辨别】
- Input:
- Output:金
- Input:
Face recognition 【人脸识别】
- Input: image of a face
- output: person
Classification:Example Application
【图】
如上图,Pokemon又来啦! Pokemon有很多属性,比如皮卡丘是电属性,杰尼龟是水属性之类。
关于Pokemon的Classification:Predict the “type” of Pokemon based on the information
Input:Information of Pokemon (数值化)
Output:the type
Training Data: ID在前400的Pokemon

Testing Data: ID在400后的Pokemon
Classification as Regression?
1. 简化问题,只考虑二分类:Class 1 , Class2。
如果把分类问题当作回归问题,把类别数值化。
在Training中: Class 1 means the target is 1; Class 2 means the target is -1.
在Testing中:如果Regression的函数值接近1,说明是class 1;如果函数值接近-1,说明是class 2.
Regression:输入信息只考虑两个特征。
Model:$y=w_1x_1+w_2x_2+b$
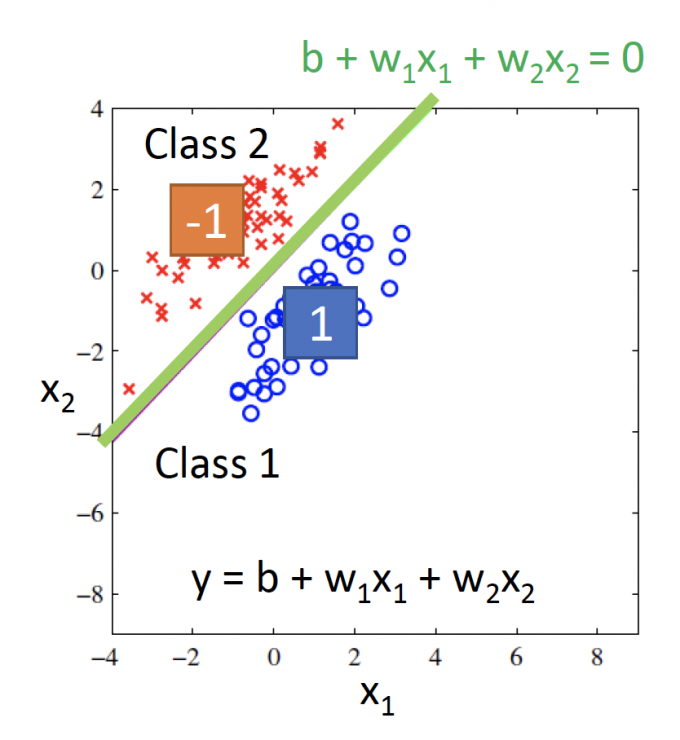
当Training data的分布如上图所示时,得到的(最优函数)分界线感觉很合理。
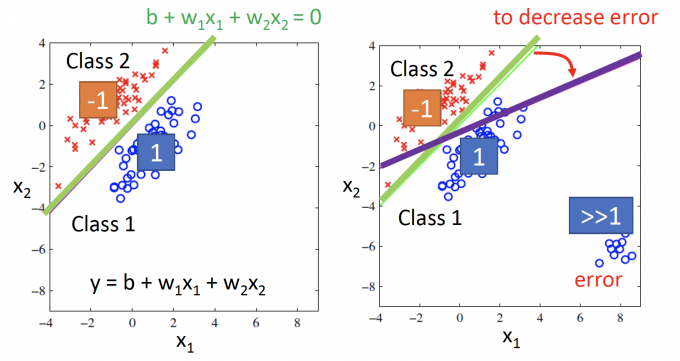
但当Training data在右下角也有分布时(如右图),训练中为了减少error,训练得到的分界线会变成紫色的那一条。
所以,如果用Regression来做Classification:Penalize to the examples that are “too correct” .[1]
训练中会因为惩罚一些“过于正确”(即和我们假定的target离太远)的example,得到的最优函数反而have bad performance.
2. 此外,如果用Regression来考虑多分类。
Multiple class: Class 1 means the target is 1; Class 2 means the target is 2; Class 3 means the target is 3……
如果用上面这种假设,可以认为Class 3和Class 2 的关系更近,和Class 1的关系更远一些。但实际中,可能这些类别have no relation。
Classification: Ideal Alternatives
在上面,我们假设二元分类每一个类别都有一个target,结果不尽人意。
如果将模型改为下图形式,也可以解决分类问题。(挖坑)[2]

Generative Model(生成模型)
Estimate the Probabilities
用概率的知识来考虑分类这个问题,如下图所示,有两个两个类别,C1和C2。
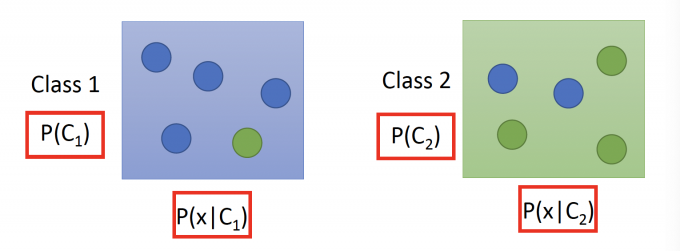
在Testing中,如果任给一个x,属于C1的概率是(贝叶斯公式)
$$ P\left(C_{1} | x\right)=\frac{P\left(x | C_{1}\right) P\left(C_{1}\right)}{P\left(x | C_{1}\right) P\left(C_{1}\right)+P\left(x | C_{2}\right) P\left(C_{2}\right)} $$所以在Training应该知道这些的概率: $P(C_1),P(x|C_1),P(C_2),P(x|C_2)$
先验概率P(C1)和P(C2)很容易得知。
而似然P(x|C1)和P(x|C2)的概率应该如何得知呢?
如果能假设:类别是C1中的变量x服从某种分布,如高斯分布等,即可以得到任意P(x|C1)的值。
所以Generative Model:是对examples假设一个分布模型,在training中调节分布模型的参数,使得examples出现的概率最大。(极大似然的思想)
Prior Probabilities(先验概率)
先只考虑Water和Normal两个类别。
先验概率:即通过过去资料分析得到的概率。
在Pokemon的例子中,Training Data是ID<400的水属性和一般属性的Pokemon信息。
Training Data:79 Water,61 Normal。
得到的先验概率 P(C1)=79/(79+61)=0.56, P(C2)=61/(79+61)=0.44。
Probability from Class
先只考虑Defense和SP Defense这两个feature。
如果不考虑生成分布模型,在testing中直接计算P(x|Water)的概率,如下图右下角的那只龟龟,在training data中没有出现过,那值为0吗?显然不对。
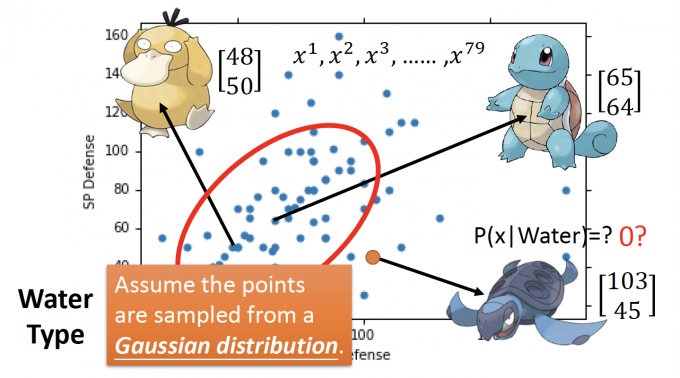
假设:上图中water type的examples是从Gaussian distribution(高斯分布)中取样出来的。
因此在training中通过training data得到最优的Gaussian distribution的参数,计算样本中没有出现过的P(x|Water)也就迎刃而解了。
Gaussian Distribution
多维的高斯分布(高斯分布就是正态分布啦)的联合概率密度:
$$ f_{\mu, \Sigma}(x)=\frac{1}{(2 \pi)^{D / 2}} \frac{1}{|\Sigma|^{1 / 2}} \exp \left\{-\frac{1}{2}(x-\mu)^{T} \Sigma^{-1}(x-\mu)\right\} $$D: 维数
$\mu$ : mean
$\Sigma$ :covariance matrix(协方差矩阵)
协方差: $ cov(X,Y)=E[[X-E(X)][Y-E(Y)]]=E(XY)-E(X)E(Y)$
具体协方差性质,查阅概率论课本吧。
x: vector,n维随机变量
高斯分布的性质只和 $\mu$ 和 $\Sigma$ 有关。
$\Sigma$ 一定时,$\mu$ 不同,如下图:
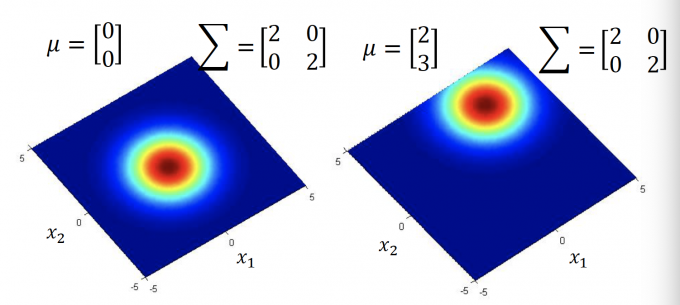
$\mu$ 一定, $\Sigma$ 不同时,如下图:
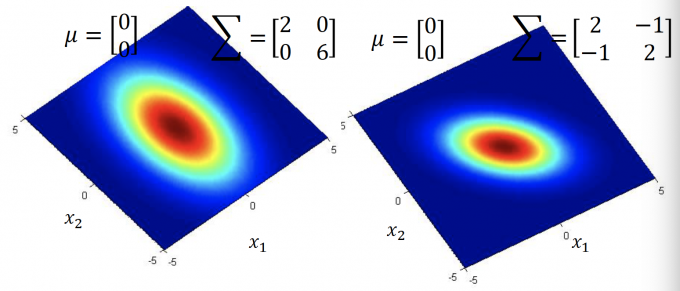
Maximum Likelihood(极大似然)
样本分布如下图所示,假设这些样本是从Gaussian distribution中取样,那如何在训练中得到高斯分布的 $\mu$ 和 $\Sigma$ 呢?
极大似然估计。
考虑Water,有79个样本,估计函数 $L(\mu, \Sigma)=f_{\mu, \Sigma}\left(x^{1}\right) f_{\mu, \Sigma}\left(x^{2}\right) f_{\mu, \Sigma}\left(x^{3}\right) \ldots \ldots f_{\mu, \Sigma}\left(x^{79}\right)$
极大似然估计,即找到 $f_{\mu, \Sigma}(x)=\frac{1}{(2 \pi)^{D / 2}} \frac{1}{|\Sigma|^{1 / 2}} \exp \left\{-\frac{1}{2}(x-\mu)^{T} \Sigma^{-1}(x-\mu)\right\}$ 中的 $\mu$ 和$\Sigma$ 使得估计函数最大(使得取出这些样本的概率最大化)。
$\mu^{*}, \Sigma^{*}=\arg \max _{\mu, \Sigma} L(\mu, \Sigma)$
求导计算(过于复杂,但也不是不能做是吧)
背公式[3]
$\mu^{*}=\frac{1}{79} \sum_{n=1}^{79} x^{n} \qquad \Sigma^{*}=\frac{1}{79} \sum_{n=1}^{79}\left(x^{n}-\mu^{*}\right)\left(x^{n}-\mu^{*}\right)^{T}$
得到Water和Normal的高斯分布,如下图:
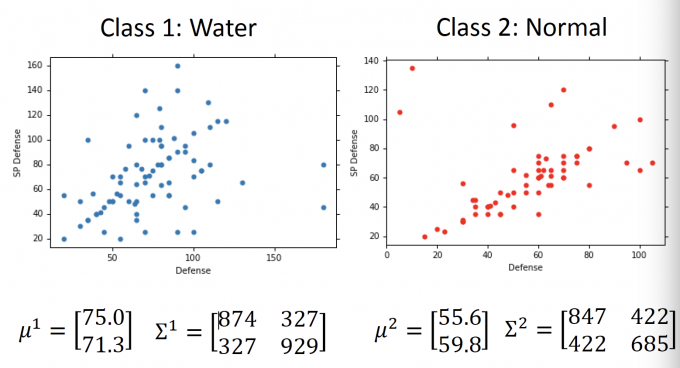
Do Classification: different $\Sigma$
Testing
Testing: $P\left(C_{1} | x\right)=\frac{P\left(x | C_{1}\right) P\left(C_{1}\right)}{P\left(x | C_{1}\right) P\left(C_{1}\right)+P\left(x | C_{2}\right) P\left(C_{2}\right)}$
P(x|C1)由训练得出的Water的高斯分布计算出,P(x|C2)由Normal的高斯分布计算出。(如下图,过于难打)
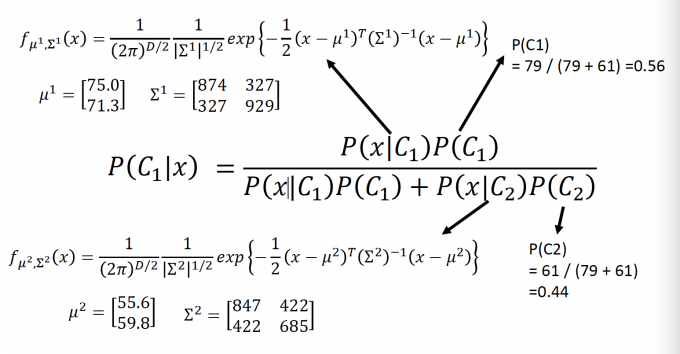
如果P(C1|x)>0.5,说明x 属于Water(Class 1)。
Results
如果只考虑两个feature(Defense和SP Defense),下图是testing data的样本图,蓝色属于Water,红色属于Normal。
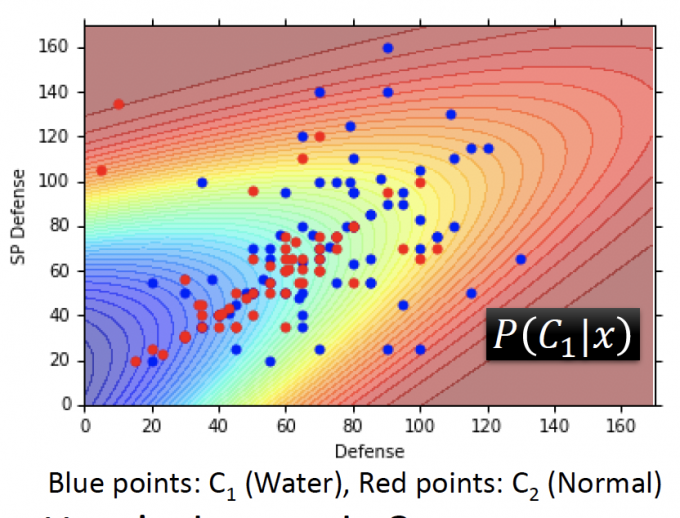
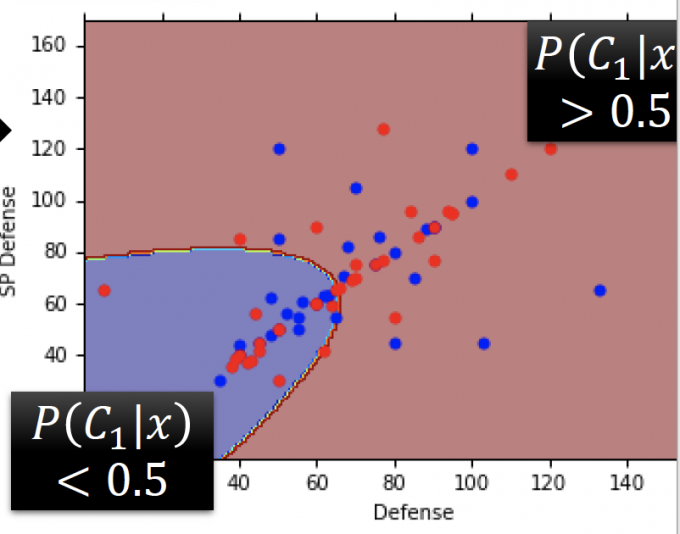
用训练得出的模型,Testing Data: 47% accuracy。(结果如下图)
如果考虑全部features(7个),重新训练出的模型,结果:Testing Data:54% accuracy。(结果如下图)
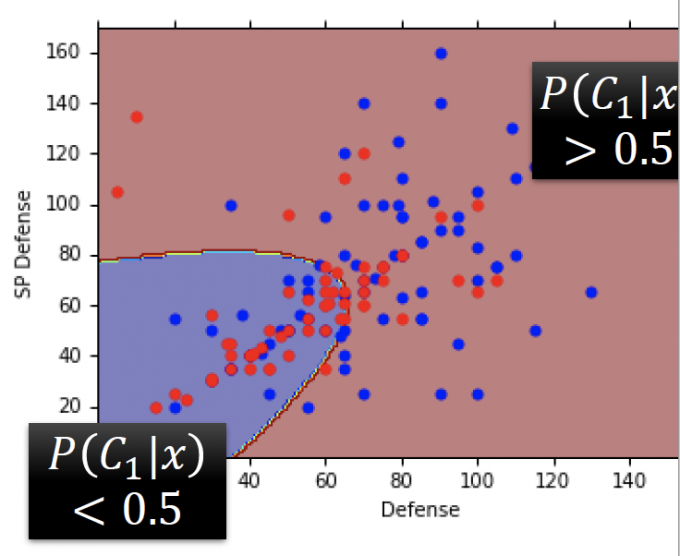
结果并不好。参数过多,模型过于复杂,有些过拟合了。
Modifying Model:same $\Sigma$
模型中的参数有两个的Gaussian Distribution中的 $\mu^* $ 和 $\Sigma^*$ ,其中协方差矩阵的大小等于feature的平方,所以让不同的class share 同一个 $\Sigma$ ,以此来减少参数,简化模型。
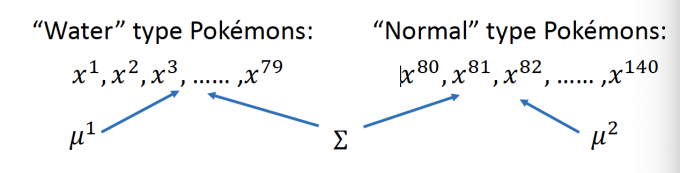
极大似然估计的估计函数:
$$ L\left(\mu^{1}, \mu^{2}, \Sigma\right)=f_{\mu^{1}, \Sigma}\left(x^{1}\right) f_{\mu^{1}, \Sigma}\left(x^{2}\right) \cdots f_{\mu^{1}, \Sigma}\left(x^{79}\right)\times f_{\mu^{2}, \Sigma}\left(x^{80}\right) f_{\mu^{2}, \Sigma}\left(x^{81}\right) \cdots f_{\mu^{2}, \Sigma}\left(x^{140}\right) $$公式推导:[3]
$\mu$ 的公式不变。
$\Sigma=\frac{79}{140} \Sigma^{1}+\frac{61}{140} \Sigma^{2}$ ,即是原 $\Sigma^1\ \Sigma^2$的加权平均。Results
当只考虑两个features,用同样的协方差参数,结果如下图:
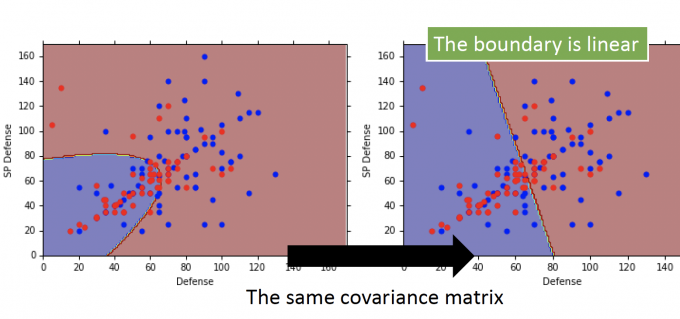
可以发现,用了同样的协方差矩阵参数后,边界变成了线性的,所以这也是一个线性模型。
再考虑7个features,用同样的协方差矩阵参数,模型也是线性模型,但由于在高维空间,人无法直接画出其boundary,这也是机器学习的魅力所在,能解决一些人无法解决的问题。
结果:从之前的54% accuracy增加到 73% accurancy.
结果明显变好了。
Summary
Three Steps:
Function Set(Model):

Goodness of a function:
The mean µ and convariance $\Sigma$ that maximizing the likelihood(the probability of generating data)
Find the best function:easy(公式)
Appendix
为什么要选择Gaussian Distribution
You can always use the distribution you like.
可以选择你喜欢的任意分布,t分布,开方分布等。
(老师说:如果我选择其他分布,你也会问这个问题,h h h)
Naive Bayes Classifier
If you assume all the dimensions are independent, then you are using Naive Bayes Classifier.
如果假设features之间互相独立, $P\left(x | C_{1}\right)=P\left(x_{1} | C_{1}\right) P\left(x_{2} | C_{1}\right) \quad \ldots \ldots \quad P\left(x_{k} | C_{1}\right) $ 。
xi是x第i维度的feature。
对于每一个 P(xi|C1),可以假设其服从一维高斯分布。如果是binary features(即feature取值只有两个),也可以假设它服从Bernoulli distribution(贝努利分布)。
Posterior Probability(后验概率)
Posterior Probability后验概率,即使用贝叶斯公式,已知结果,寻找最优可能导致它发生的原因。
对 $P\left(C_{1} | x\right)=\frac{P\left(x | C_{1}\right) P\left(C_{1}\right)}{P\left(x | C_{1}\right) P\left(C_{1}\right)+P\left(x | C_{2}\right) P\left(C_{2}\right)}$ 进行处理。
得到:
$$ \begin{equation} \begin{aligned} P\left(C_{1} | x\right)&=\frac{P\left(x | C_{1}\right) P\left(C_{1}\right)}{P\left(x | C_{1}\right) P\left(C_{1}\right)+P\left(x | C_{2}\right) P\left(C_{2}\right)}\\ &=\frac{1}{1+\frac{P\left(x | C_{2}\right) P\left(C_{2}\right)}{P\left(x | C_{1}\right) P\left(C_{1}\right)}}\\&=\frac{1}{1+\exp (-z)} =\sigma(z) \qquad(z=\ln \frac{P\left(x | C_{1}\right) P\left(C_{1}\right)}{P\left(x | C_{2}\right) P\left(C_{2}\right)} \end{aligned} \end{equation} $$Worning of Math
- $z=\ln \frac{P\left(x | C_{1}\right) P\left(C_{1}\right)}{P\left(x | C_{2}\right) P\left(C_{2}\right)}=\ln \frac{P\left(x | C_{1}\right)}{P\left(x | C_{2}\right)}+\ln \frac{P\left(C_{1}\right)}{P\left(C_{2}\right)}$
- $\ln \frac{P\left(C_{1}\right)}{P\left(C_{2}\right)}=\frac{\frac{N_{1}}{N_{1}+N_{2}}}{\frac{N_{2}}{N_{1}+N_{2}}}=\frac{N_{1}}{N_{2}}$
- $P\left(x | C_{1}\right)=\frac{1}{(2 \pi)^{D / 2}} \frac{1}{|\Sigma 1|^{1 / 2}} \exp \left\{-\frac{1}{2}\left(x-\mu^{1}\right)^{T}\left(\Sigma^{1}\right)^{-1}\left(x-\mu^{1}\right)\right\}$
- $P\left(x | C_{2}\right)=\frac{1}{(2 \pi)^{D / 2}} \frac{1}{\left|\Sigma^{2}\right| 1 / 2} \exp \left\{-\frac{1}{2}\left(x-\mu^{2}\right)^{T}\left(\Sigma^{2}\right)^{-1}\left(x-\mu^{2}\right)\right\}$
- $\ln \frac{\left|\Sigma^{2}\right|^{1 / 2}}{\left|\Sigma^{1}\right|^{1 / 2}}-\frac{1}{2}\left[\left(x-\mu^{1}\right)^{T}\left(\Sigma^{1}\right)^{-1}\left(x-\mu^{1}\right)-\left(x-\mu^{2}\right)^{T}\left(\Sigma^{2}\right)^{-1}\left(x-\mu^{2}\right)\right]$
- $\left(x-\mu^{1}\right)^{T}\left(\Sigma^{1}\right)^{-1}\left(x-\mu^{1}\right)=x^{T}\left(\Sigma^{1}\right)^{-1} x-2\left(\mu^{1}\right)^{T}\left(\Sigma^{1}\right)^{-1} x+\left(\mu^{1}\right)^{T}\left(\Sigma^{1}\right)^{-1} \mu^{1}$
- $\left(x-\mu^{2}\right)^{T}\left(\Sigma^{2}\right)^{-1}\left(x-\mu^{2}\right)=x^{T}\left(\Sigma^{2}\right)^{-1} x-2\left(\mu^{2}\right)^{T}\left(\Sigma^{2}\right)^{-1} x+\left(\mu^{2}\right)^{T}\left(\Sigma^{2}\right)^{-1} \mu^{2}$
- $\begin{aligned} z=& \ln \frac{\left|\Sigma^{2}\right|^{1 / 2}}{\left|\Sigma^{1}\right|^{1 / 2}}-\frac{1}{2} x^{T}\left(\Sigma^{1}\right)^{-1} x+\left(\mu^{1}\right)^{T}\left(\Sigma^{1}\right)^{-1} x-\frac{1}{2}\left(\mu^{1}\right)^{T}\left(\Sigma^{1}\right)^{-1} \mu^{1} \\ &+\frac{1}{2} x^{T}\left(\Sigma^{2}\right)^{-1} x-\left(\mu^{2}\right)^{T}\left(\Sigma^{2}\right)^{-1} x+\frac{1}{2}\left(\mu^{2}\right)^{T}\left(\Sigma^{2}\right)^{-1} \mu^{2}+\ln \frac{N_{1}}{N_{2}} \end{aligned}$
简化模型后, $\Sigma^1=\Sigma^2=\Sigma$ :
$$ z=\left(\mu^{1}-\mu^{2}\right)^{T} \Sigma^{-1} x-\frac{1}{2}\left(\mu^{1}\right)^{T} \Sigma^{-1} \mu^{1}+\frac{1}{2}\left(\mu^{2}\right)^{T} \Sigma^{-1} \mu^{2}+\ln \frac{N_{1}}{N_{2}} $$令 $w^T=\left(\mu^{1}-\mu^{2}\right)^{T} \Sigma^{-1} \qquad b=-\frac{1}{2}\left(\mu^{1}\right)^{T} \Sigma^{-1} \mu^{1}+\frac{1}{2}\left(\mu^{2}\right)^{T} \Sigma^{-1} \mu^{2}+\ln \frac{N_{1}}{N_{2}}$
当简化模型后,z是线性的,这也是为什么在之前的结果中边界是线性的原因。
最后模型变成这样: $P\left(C_{1} | x\right)=\sigma(w \cdot x+b)$ .
在生成模型中,我们先估计出 $\mu_1\ \mu_2\ N_1\ N_2\ \Sigma$ 的值,也就得到了 $w\ b$ 的值。
那,我们能不能跳过 $\mu_1\ \mu_2\ N_1\ N_2\ \Sigma$ ,直接估计 $w\ b$ 呢?
在下一篇博客[4]中会继续Classification。
Reference
Classification as Regression: Bishop, P186.
挖坑:Classification:Perceptron,SVM.
Maximum likelihood solution:Bishop chapter4.2.2
「机器学习-李宏毅」:Classification-Probabilistic Generative Model

