「机器学习-李宏毅」:Classification-Logistic Regression
在上篇文章中,讲解了怎么用Generative Model做分类问题。
这篇文章中,讲解了做Classification的另一种Discriminative的方式,也就是Logistic Regression。
文章主要有两部分:
第一部分讲解了Logistic Regression的三个步骤。
第二个部分讲解了multi-class多分类的三个步骤,以及softmax是如何操作的。
Logistic Regression
Step1: Function Set
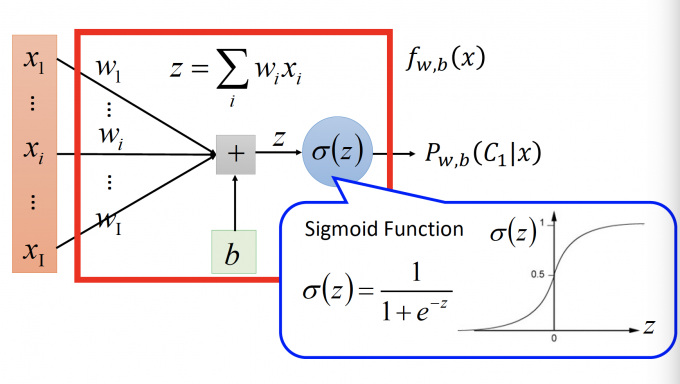
在Post not found: Classification 上一篇文章末尾,我们得出 $P_{w, b}\left(C_{1} | x\right)=\sigma(w\cdot x+b)$ 的形式,想跳过找 $\mu_1,\mu_2,\Sigma$ 的过程,直接找 $w,b$ 。
因此Function Set: $f_{w, b}(x)=P_{w, b}\left(C_{1} | x\right)$ 。值大于0.5,则属于C1类,否则属于C2类。
Step2: Goodness of a Function
使用极大似然的思想(在前一篇机率模型/生成模型中有讲)
估计函数是 :$L(w, b)=f_{w, b}\left(x^{1}\right) f_{w, b}\left(x^{2}\right)\left(1-f_{w, b}\left(x^{3}\right)\right) \cdots f_{w, b}\left(x^{N}\right)$
目标: $ w^{*}, b^{*}=\arg \max _{w, b} L(w, b)$
由于在之前的Regression中,我们都是找极小值点,为了方便处理,将估计函数转换为如下形式的损失函数:
$$ \begin{equation} \begin{aligned} -\ln L(w, b)&=-(\ln f_{w, b}\left(x^{1}\right)+\ln f_{w, b}\left(x^{2}\right)+\ln \left(1-f_{w, b}\left(x^{3}\right)\right) \cdots ) \\ Loss&=\sum_{n}-\left[\hat{y}^{n} \ln f_{w, b}\left(x^{n}\right)+\left(1-\hat{y}^{n}\right) \ln \left(1-f_{w, b}\left(x^{n}\right)\right)\right] \end{aligned} \end{equation} $$目标 : $w^{*}, b^{*}=\arg \min _{w, b} L(w, b)$
Cross entropy(交叉熵)
关于熵、交叉熵、相对熵(KL散度)的理解:强烈安利
上式中的 $\left[\hat{y}^{n} \ln f_{w, b}\left(x^{n}\right)+\left(1-\hat{y}^{n}\right) \ln \left(1-f_{w, b}\left(x^{n}\right)\right)\right]$ 其实是两个Bernoulli distribution的交叉熵。
交叉熵是什么? 简单来说,交叉熵是评估两个distribution 有多接近。所以当这两个Bernoulli 分布的交叉熵为0时,表明这两个分布一模一样。
对于 $\hat{y}^{n} \ln f_{w, b}\left(x^{n}\right)+\left(1-\hat{y}^{n}\right) \ln \left(1-f_{w, b}\left(x^{n}\right)\right)$ :
Distribution p: p(x = 1) = $\hat{y}^n$ ; p( x = 0 ) = 1 - $\hat{y}^n$
Distribution q: q(x = 1 ) = $f(x^n)$ ; q(x = 0 ) = 1 - $f(x^n)$
交叉熵 $H(p,q)=-\Sigma_xp(x)\ln(q(x))$
p是真实的分布,q是预测的分布。
因此,这个损失函数的表达式其实也是输出分布和target分布的交叉熵,即:
$L(f)=\sum_{n} C\left(f\left(x^{n}\right), \hat{y}^{n}\right)$
( $C\left(f\left(x^{n}\right), \hat{y}^{n}\right)=-\left[\hat{y}^{n} \ln f\left(x^{n}\right)+\left(1-\hat{y}^{n}\right) \ln \left(1-f\left(x^{n}\right)\right)\right]$ )
和Linear Regression不同,为什么Logistic Regression不用square error,而要使用cross entropy。
在1.4小节会给出解释。
Step3: Find the best function
在第三步,同样使用Gradient来寻找最优函数。
推导过程:
$\left.\frac{-\ln L(w, b)}{\partial w_{i}}=\sum_{n}-\left[\hat{y}^{n} \frac{\ln f_{w, b}\left(x^{n}\right)}{\partial w_{i}}+\left(1-\hat{y}^{n}\right) \frac{\ln \left(1-f_{w, b}\left(x^{n}\right)\right.}{\partial w_{i}}\right)\right]$
$\frac{\partial \ln f_{w, b}(x)}{\partial w_{i}}=\frac{\operatorname{\partial\ln} f_{w, b}(x)}{\partial z} \frac{\partial z}{\partial w_{i}}$
- $\frac{\partial \ln \sigma(z)}{\partial z}=\frac{1}{\sigma(z)} \frac{\partial \sigma(z)}{\partial z}=\frac{1}{\sigma(z)} \sigma(z)(1-\sigma(z))$
- $\frac{\partial z}{\partial w_{i}}=x_{i}$
$\frac{\partial \ln \left(1-f_{w, b}(x)\right)}{\partial w_{i}}=\frac{\operatorname{\partial\ln}\left(1-f_{w, b}(x)\right)}{\partial z} \frac{\partial z}{\partial w_{i}}$
- $\frac{\partial \ln (1-\sigma(z))}{\partial z}=-\frac{1}{1-\sigma(z)} \frac{\partial \sigma(z)}{\partial z}=-\frac{1}{1-\partial(z)} \sigma(z)(1-\sigma(z))$
- $\frac{\partial z}{\partial w_{i}}=x_{i}$
$\frac{\partial \sigma(z)}{\partial z}=\sigma(z)\cdot(1-\sigma(z))$
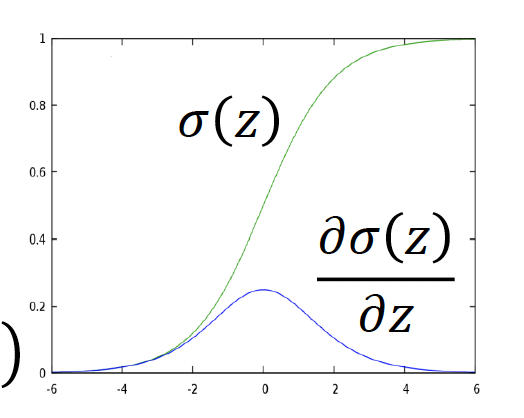
注:$f_{w, b}(x)=\sigma(z)$ ; $z=w \cdot x+b=\sum_{i} w_{i} x_{i}+b$
- $$ \begin{equation} \begin{aligned} \frac{-\ln L(w, b)}{\partial w_{i}}&=\sum_{n}-\left[\hat{y}^{n}\left(1-f_{w, b}\left(x^{n}\right)\right) x_{i}^{n}-\left(1-\hat{y}^{n}\right) f_{w, b}\left(x^{n}\right) x_{i}^{n}\right] \\&=\sum_{n}-\left(\hat{y}^{n}-f_{w, b}\left(x^{n}\right)\right) x_{i}^{n} \end{aligned} \end{equation} $$
因此Logistic Regression的损失函数的导数和Linear Regression的一样。
迭代更新: $w_{i} \leftarrow w_{i}-\eta \sum_{n}-\left(\hat{y}^{n}-f_{w, b}\left(x^{n}\right)\right) x_{i}^{n}$
与Linear Regression 的对比
如图所示。

If : Logistic + Square Error
前面一小节我们提到,在Logistic Regression中使用cross entropy判别一个函数的好坏,那为什么不使用square error来judge the goodness?
如果使用 Square Error的方法,步骤如下:
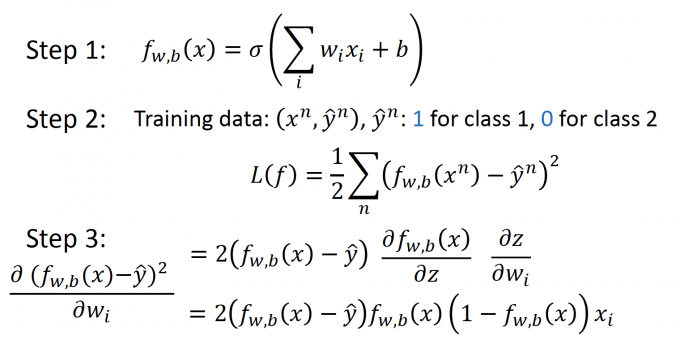
来看Step 3: 损失函数的导数是 $2\left(f_{w, b}(x)-\hat{y}\right) f_{w, b}(x)\left(1-f_{w, b}(x)\right) x_{i}$
考虑 $\hat{y}^n=1$ (即我们的target是1):
- 如果 $f_{w,b}(x^n)=1$ , 即预测值接近 target, 算出来的 $\partial{L}/\partial{w_i}=0$ 是期望的。
- 如果 $f_{w,b}(x^n)=0$ , 即预测值原理 target, 算出来的 $\partial{L}/\partial{w_i}=0$ 是不期望的。
同理,当考虑 $\hat{y}^n=0$ 情况时,也是如此。
更直观的看:
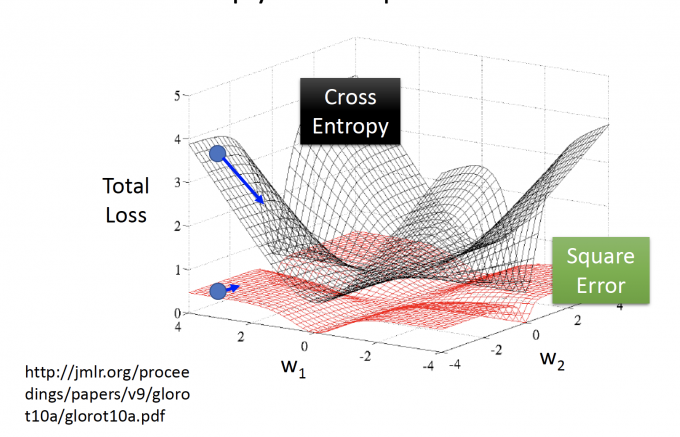
上图中,画出了两种损失函数的平面,中心的最低点是我们的target。
但在Square Error中,远离target的蓝色点,也处在很平坦的位置,其导数小,参数的更新会很慢。
因此在Cross Entropy中,离target越远,其导数更大,更新更快。
所以Cross Entropy的效果比Square Error更快,效果更好。
Discriminative V.S. Generative
这篇文章中的Logistic Regression是Discriminative Model。
上篇文章中Classification是Generative Model。有什么区别呢?

上图中,Generative Model做了假设(脑补),假设它是 Gaussian Distribution,假设它是Bernoulli Distribution。然后去找这些分布的参数,在求出 $w,b$。
而在Discriminative Model中,没有做任何假设,直接找 $w,b$ 参数。
所以,这两种Model经过training找出来的参数一样吗?
答案是不一样的。
The same model(function set), but different function is selected by the same training data.
在上篇Pokemon的例子中,比较两种方法的结果差异。
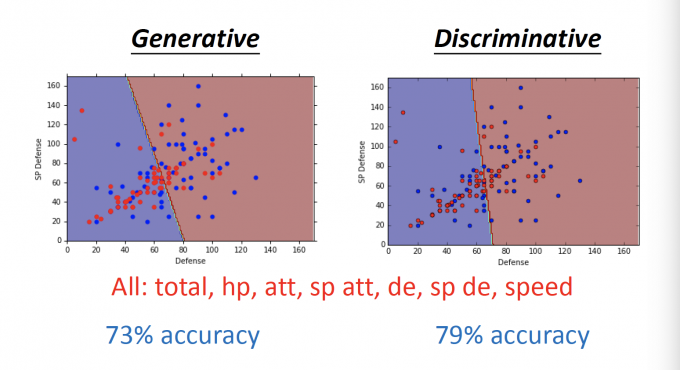
可见,在Pokemon的例子总,Discriminative的效果比Generative的效果好一些。
但是Generative Model就不好吗?
Benefit of generative model
With the assumption of probability distribution, less training data is needed.
【训练生成模型所需数据更少】
With the assumption of probability distribution, more robust to the noise.
【生成模型对noise data更兼容】
Priors and class-dependent probabilities can be estimated from different sources.
【生成模型中的 先验概率Priors 和 基于类别的分布概率不同】
比如,做语音辨识系统,整个系统是generative的。
因为Prior(某一句话的概率)并不需要从data中知道,可以直接在网络上爬虫统计。
而class-dependent probabilities(这段语音是这句话的概率)需要data进行训练才能得知。
Multi-class classification
softmax
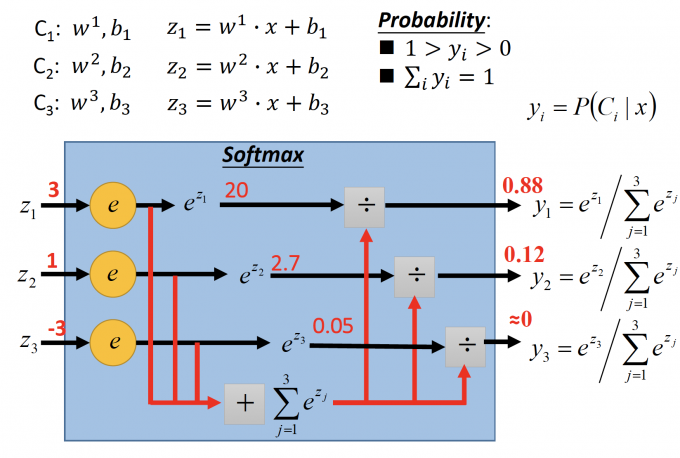
假设有三个类别:C1、C2、C3 。模型已经得到,参数分别是 w、b。
对于输入x, 判断x属于哪一个类别。
- 通过每个类别的 w、b求出 $z^i=w^i\cdot x+b_i$
Softmax的步骤:
- exponential:每个z值得到 $=e^z$ .
- sum:将指数化后的值加起来$=\Sigma_{j=1}^3e^{z_j}$
- output: 每个类别的输出 $y_i=e^{z_1}/\Sigma_{j=1}^3e^{z_j}$ ,即x属于类别i的概率。
求出的 $1>y_i>0$ 且 $\Sigma_iy_i=1$ 。
通过Softmax,得到 $y_i=P(C_i|x)$ 。
Steps
(手写笔记,略倾斜,原来不切一切还不知道自己歪的这么厉害 泪)
Step 1:
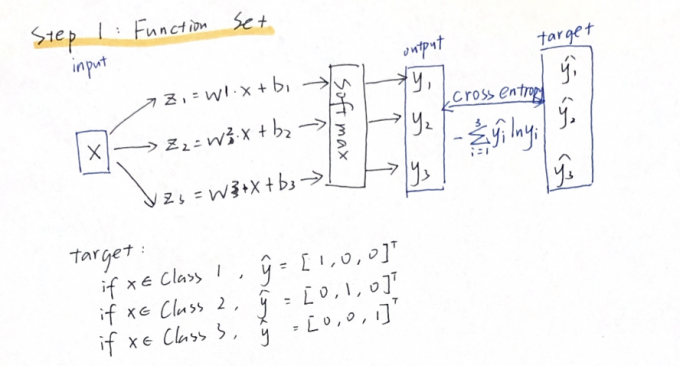
Step 2:
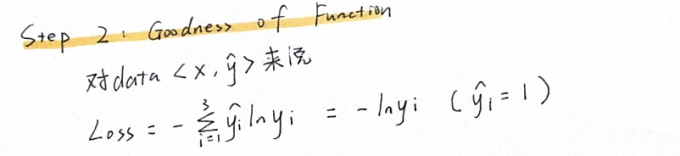
Step 3:

使用Stochastic Gradient(即每个样本更新一次)的话:
data: [x, $\hat{y}$ ] , $\hat{y}_i=1$
更新 $w^j$ :
$j=i$ :
$w^j \leftarrow w^j-\eta\cdot (y_i-1)\cdot x$
$j\neq i$ :
$w^j \leftarrow w^j-\eta\cdot y_i\cdot x$
(下次一定,笔记写直一点!)
更为规范的推导见[1]
Limitation of Logistic Regression
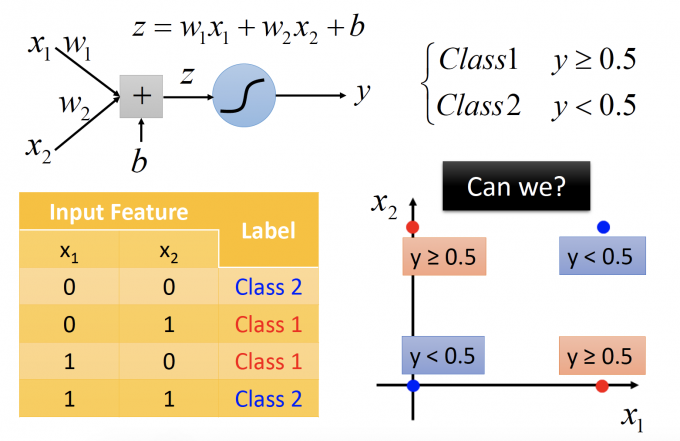
对于如上情况,Logistic Regression并不能进行分类,因为他的boundary 应该是线性的。
Feature Transforming
如果对feature做转换后,就可以用Logistic Regression处理。
重定义feature, $x_1’$ :定义为到[0,0]的距离, $x_2’$ :定义为到[1,1]的距离。
于是图变成下图,即可用Logistic Regression进行分类。
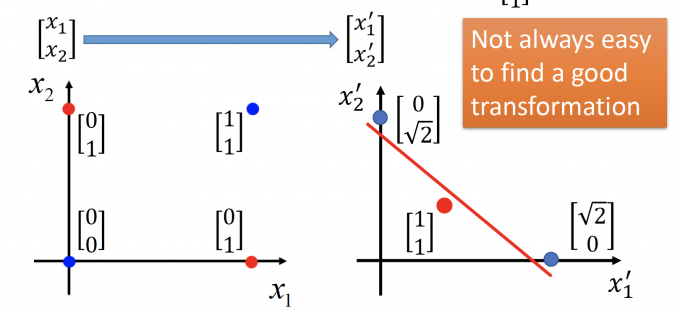
但这样的做法,就不像人工智能了,因为Feature Transformation需要人来设计,而且较难设计。
Cascading logistic regression models
另一种做法是,将logistic regression连接起来。
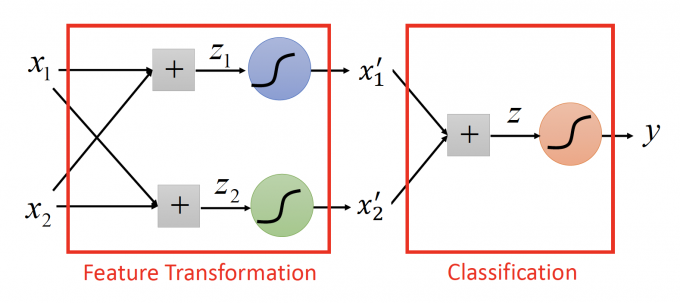
上图中,左边部分的两个logistic regression就相当于在做Feature Transformation,右边部分相当于在做Classification。
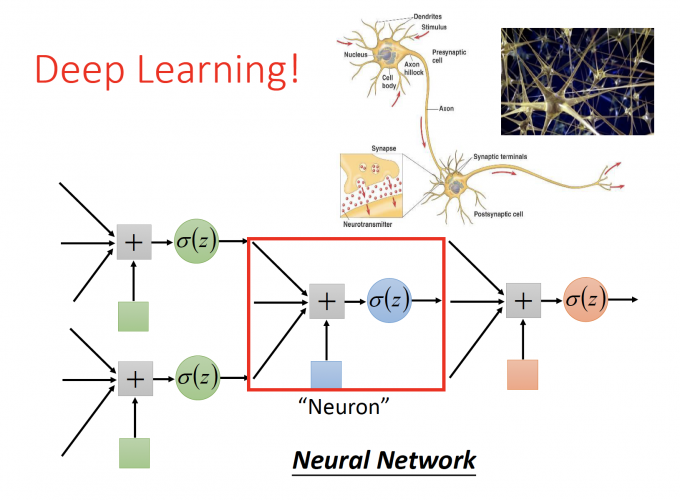
而通过这种形式,将多个model连接起来,也就是大热的Neural Network。
Reference
Multi-class Classification推导:Bishop,P209-210
关于Entropy, Cross Entropy, KL-Divergence的理解:强烈安利:https://www.youtube.com/watch?v=ErfnhcEV1O8
「机器学习-李宏毅」:Classification-Logistic Regression

