「机器学习-李宏毅」：Backpropagation
这篇文章中，讲解了Deep Learning中使用的一种高效Gradient Descent的算法：BackPropagation。
BackPropagation通过正向传播和反向传播两个阶段，最后能一起算出损失函数对每一个参数的gradient。
Gradient Descent
在Neural Network中，参数的更新也是通过Gradient Descent。
但是当Neural Network层数很深，结构很复杂的时候，会有millions of parapmeters。
Backpropagation：To compute the gradient efficiently.
Chain Rule
BP中需要用到的数学知识：微积分中的链式法则。
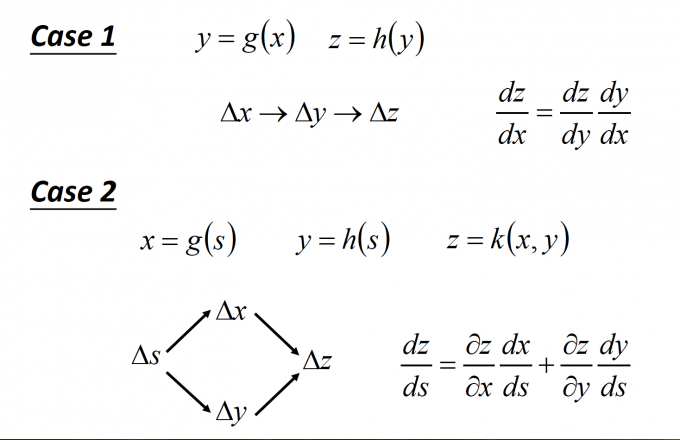
Backpropagation
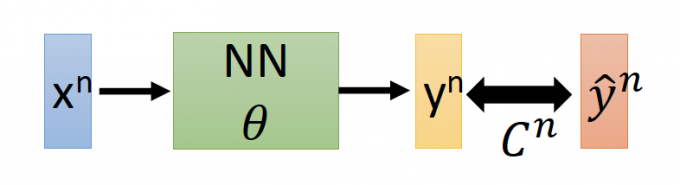
在NN中，定义损失函数 $L(\theta)=\sum_{n=1}^{N} C^{n}(\theta)$
（$\theta$ 代指NN中所有的weight 和bias，$C$ 为Cross-entropy）
对某一参数的gradient为 $\frac{\partial L(\theta)}{\partial w}=\sum_{n=1}^{N} \frac{\partial C^{n}(\theta)}{\partial w}$
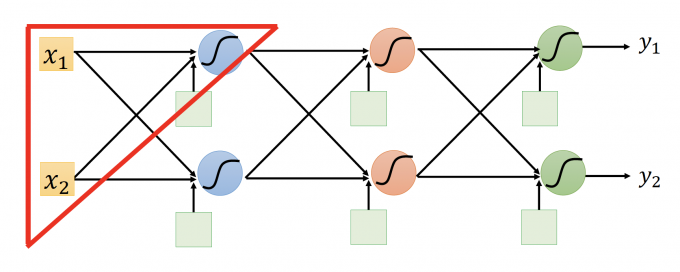
在上图NN中，我们先只研究红框部分，即是以下结构：
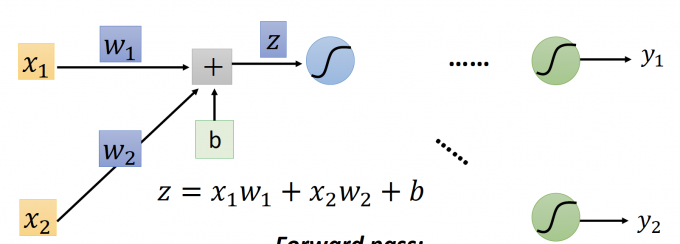
z：每个activation function的输入。
根据链式法则， $\frac{\partial C}{\partial w}= \frac{\partial z}{\partial w} \frac{\partial C}{\partial z}$ .
要计算每个参数的 $\frac{\partial C}{\partial w}$ ，分为两部分。
- Forward pass: compute $\frac{\partial z}{\partial w} $ for all parameters.
- Backward pass: compute $\frac{\partial C}{\partial z} $ for all activation function inputs z.
BP：Forward pass
Compute $\frac{\partial z}{\partial w} $ for all parameters.
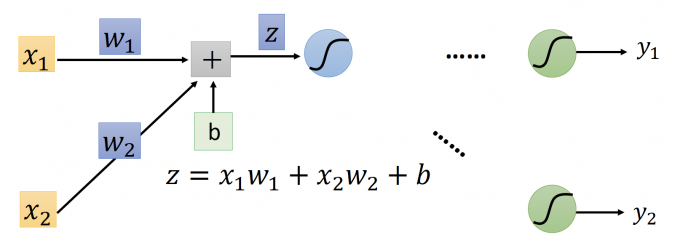
还是只看上图这一部分，可以轻易得出： $\partial{z}/\partial{w_1}=x_1\qquad \partial{z}/\partial{w_2}=x_2$
得到结论： $\frac{\partial z}{\partial w} $ 等于 the value of the input connected by the weight.
【$\frac{\partial z}{\partial w} $ 等于 连接w的输入的值】
那么，如何计算出NN中全部的 $\frac{\partial z}{\partial w} $ ？
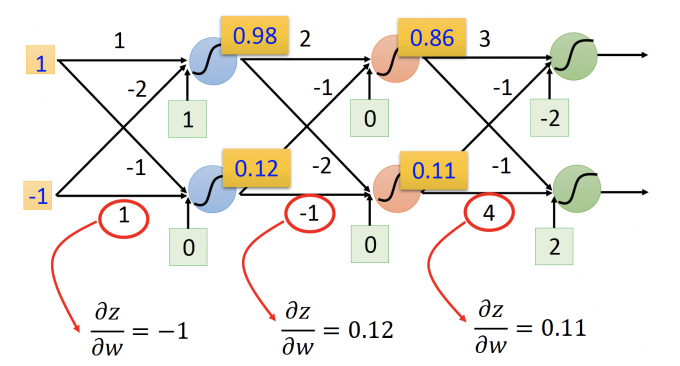
：Forward pass.
用当前参数（w,b)
从hidden layer的第一层开始，计算出第一层的输出，即第二层的输入。
依次相前计算，计算出每一层的输出，即下一层的输入，即输入所连接权重的 $\frac{\partial z}{\partial w}$ 。
BP：Backward pass
Compute $\frac{\partial C}{\partial z} $ for all activation function inputs z.
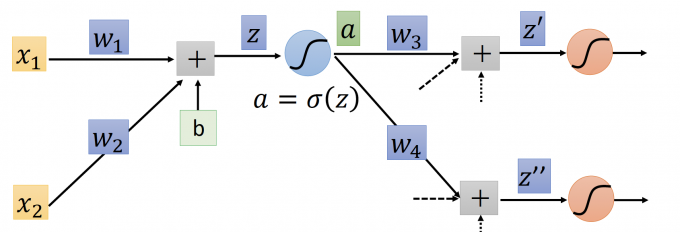
z：activation function的 input
a：activation function的 output
这里的activation function 是 sigmod函数 $a=\sigma(z)=\frac{1}{1+e^{-z}}$
要求 $\frac{\partial C}{\partial z}$ ， 再根据链式法则： $\frac{\partial C}{\partial z}=\frac{\partial a}{\partial z}\frac{\partial C}{\partial a}$
求 $\frac{\partial{a}}{\partial{z}}$ : $\frac{\partial{a}}{\partial{z}}=\sigma'(z)=\sigma(z)(1-\sigma(z))$ （是其他activation function 也能轻易求出）
求 $\frac{\partial C}{\partial a}$ ：根据链式法则： $\frac{\partial C}{\partial a}=\frac{\partial z^{\prime}}{\partial a} \frac{\partial C}{\partial z^{\prime}}+\frac{\partial z^{\prime \prime}}{\partial a} \frac{\partial C}{\partial z^{\prime \prime}}$
- $\frac{\partial z^{\prime}}{\partial a} =w_3$ ， $\frac{\partial z^{\prime\prime}}{\partial a} =w_4$
- $\frac{\partial C}{\partial z^{\prime}}$ 和 $\frac{\partial C}{\partial z^{\prime\prime}}$ ？假设，已经通过某种方法算出这个值。
- $\frac{\partial C}{\partial z}=\sigma^{\prime}(z)\left[w_{3} \frac{\partial C}{\partial z^{\prime}}+w_{4} \frac{\partial C}{\partial z^{\prime \prime}}\right]$
这个式子，可以画成一个反向传播的NN，见下图。
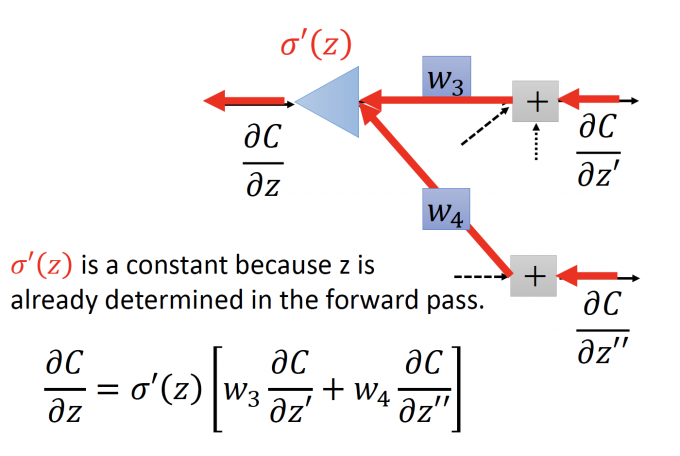$\frac{\partial C}{\partial z^{\prime}},\frac{\partial C}{\partial z^{\prime\prime}}$ 是这个neuron的输入， $w_3,w_4$ 仍然是 neuron的 weight（无bias）。
$\sigma’(z)$ 是一个常数，因为在forward pass中每一个activation的输入已经被算出来了。
和forward pass中的NN的区别是，forward 中是一个activation function，输入z作用于这个函数；
而在 backward pass中，这更像一个放缩器，将他的输入变小，即乘上一个 $\sigma’(z)$ 。
问题还是如何计算 $\frac{\partial C}{\partial z}=\sigma^{\prime}(z)\left[w_{3} \frac{\partial C}{\partial z^{\prime}}+w_{4} \frac{\partial C}{\partial z^{\prime \prime}}\right]$ ？
分为两种情况讨论， $z’,z’’$ 是否为输出层的输入？
Output Layer：
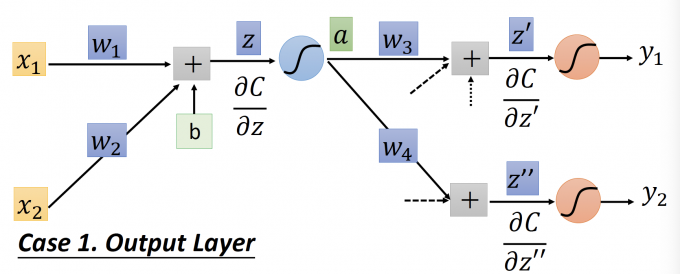
z’,z’’：activation function的输入。
y1,y2：actiavtion function（也是NN）的输出。
C：NN输出和target的cross entropy。
根据链式法则： $\frac{\partial C}{\partial z^{\prime}}=\frac{\partial y_{1}}{\partial z^{\prime}} \frac{\partial C}{\partial y_{1}} \quad \frac{\partial C}{\partial z^{\prime \prime}}=\frac{\partial y_{2}}{\partial z^{\prime \prime}} \frac{\partial C}{\partial y_{2}}$
所以，已知activation function（simod或者其他），可以轻易求出 $\frac{\partial y_{1}}{\partial z^{\prime}}(=\sigma'(z'))$ 和 $\frac{\partial y_{2}}{\partial z^{\prime\prime}}(=\sigma''(z''))$ 。
所以，已知损失函数，也可以轻易求出 $\frac{\partial C}{\partial y_1}$ 和 $\frac{\partial C}{\partial y_2}$ 。（ $C\left(y, \hat{y}\right)=-\left[\hat{y} \ln y+\left(1-\hat{y}\right) \ln \left(1-y\right)\right]$ )
所以，可以直接求出 $\frac{\partial C}{\partial z}=\sigma^{\prime}(z)\left[w_{3} \frac{\partial C}{\partial z^{\prime}}+w_{4} \frac{\partial C}{\partial z^{\prime \prime}}\right]$ 。
Not Output Layer:
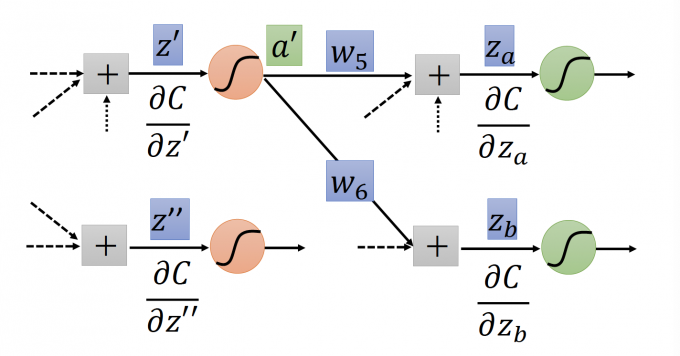
上图中，如果我们要计算 $\frac{\partial C}{\partial z’}$ ，必须要已知下一层的 $\frac{\partial C}{\partial z_a}$ ，然后一直递归下去，直到到达最后的输出层，也就是上面一种情况，可以直接计算出，再递归回来，计算当前层的 $\frac{\partial C}{\partial z’}$ 。
但是，这样计算每个参数的 $\frac{\partial{C}}{\partial{z}}$ 都要一直递归到输出层，效率显然太低了。
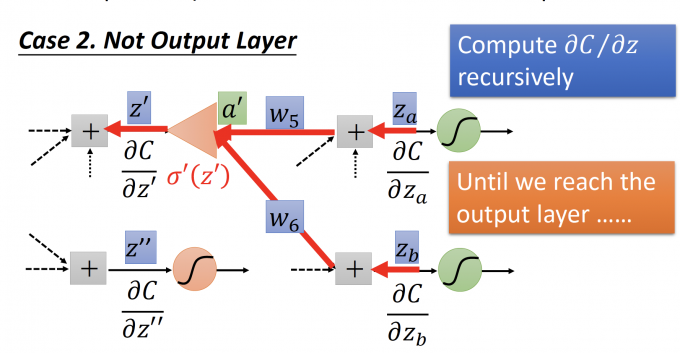
计算方法如上图：
当我们已知输出层的 $\frac{\partial{C}}{\partial{z'}},\frac{\partial{C}}{\partial{z''}}$ 时，再通过上面的步骤3（且的确算出了 $\frac{\partial{C}}{\partial{z'}},\frac{\partial{C}}{\partial{z''}}$ ），画成反向的NN，计算$\frac{\partial{C}}{\partial{z}}$.
再依次反向传播计算出每一个neuron的输出z （也是正向传播neuron的输入）的 $\frac{\partial{C}}{\partial{z}}$ .
Backforward pass 的做法：
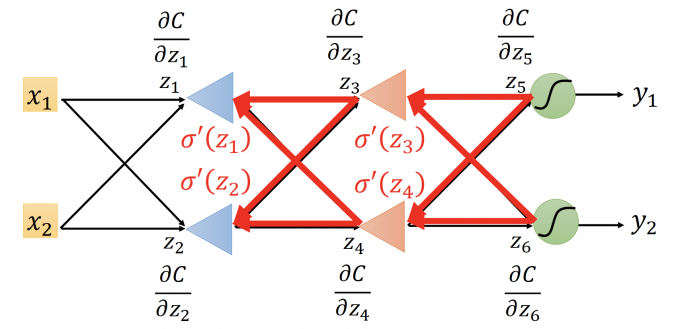
- 先计算出输出层的 $\frac{\partial{C}}{\partial{z}}$ （也就是上图的 $\frac{\partial{C}}{\partial{z_5}}$ 和 $\frac{\partial{C}}{\partial{z_6}}$ ）
- 用反向传播的NN，向后依次计算出每一层每一个neuron的 $\frac{\partial{C}}{\partial{z}}$ 。
Summary
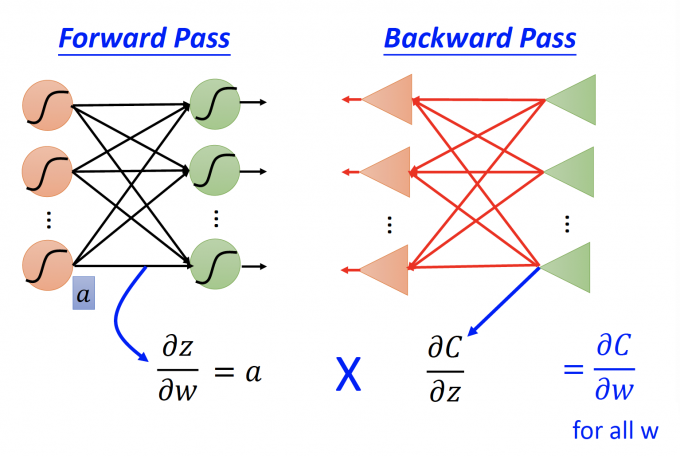
公式： $\frac{\partial z}{\partial w} \frac{\partial C}{\partial z}=\frac{\partial C}{\partial w}$
在正向传播NN中，z是neuron的activation function的输入。
在反向传播NN中，z是neuron的放缩器的输出。
通过Forward Pass计算出正向传播NN的每一个neuron的 $\frac{\partial z}{\partial w}$ ，等于该层neuron的输入。
通过Backward Pass计算出反向传播NN的每一个neuron的 $\frac{\partial C}{\partial z}$ 。
然后，通过相乘，计算出每个参数的 $\frac{\partial C}{\partial w}$。
Reference
「机器学习-李宏毅」：Backpropagation
