「Cryptography-Boneh」:Block Cipher 2
作为BlockCipher的第二篇文章。
第一部分介绍了块密码中的抽象概念PRF和PRP的安全定义。
第二部分介绍了两个概念,一个是抵抗one-time key的语义安全,另一个是抵抗many-time key(CPA)的语义安全。
在one-time key中,每条消息都使用新的密钥,类似于流密码中的OTP。介绍了不能抵抗CPA的ECB模式,还阐述了能抵抗CPA的det. CTR模式。
在many-time key中,同一条密钥可以用于加密多条消息,攻击者可以轻易具备CPA能力,文中说明了如果确定性的加密算法,则不能抵抗CPA,而random IV或者unique nonce的方式则可以抵抗CPA。
PRPs and PRFs
在前文中,有提到PRP和PRF的直觉性的定义。现在我们来看他们的安全定义。
PRF:
如下图定义这样一个游戏,有挑战者和攻击者,挑战者有两个实验EXP(b),$b=0,1$。

在EXP(0)中,挑战者随机选择一个密钥K,即确定了一个伪随机函数 $f \leftarrow \mathrm{F(k, ·)}$ ;而在EXP(1)中,挑战者随机选择了一个函数 $f\leftarrow \mathrm{Funs[X, Y]} $ 。
攻击者会向挑战者发出许多输入询问 $x_1,x_2,…,x_q$ ,挑战者对于攻击者发出的询问,会随机选择 $b=0,1$ ,用 $f(x_1),f(x_2), …,f(x_q)$ 响应。
攻击者对于收到的回复,他会输出 $b’$ ,表示攻击者视角下,他认为该输出是用伪随机函数计算的(b=0),还是用随机函数计算的(b=1);定义实验的输出为EXP(b)=b’ 。
因此安全定义如下,攻击者区分输出是伪随机函数计算的还是随机函数计算的优势是neg。
Def(PRF): F is a secure PRF if for all “efficient” A:
$$
\operatorname{Adv}_{\mathrm{PRF}}[\mathrm{A}, \mathrm{F}]:=\mid \operatorname{Pr}[\operatorname{EXP}(0)=1]-\operatorname{Pr}[\operatorname{EXP}(1)=1] \quad \text{is neg.}
$$
PRP:
同理,对PRP来说,定义的游戏如下:

同理,PRP的安全定义为,攻击者区分是伪随机置换计算的还是随机置换计算的优势为neg。
Def(PRP): E is a secure PRP if for all “efficient” A:
$$
\operatorname{Adv}_{\mathrm{PRP}}[\mathrm{A}, \mathrm{E}]:=\mid \operatorname{Pr}[\operatorname{EXP}(0)=1]-\operatorname{Pr}[\operatorname{EXP}(1)=1] \quad \text{is neg.}
$$
例题:
Let X = {0,1}. Perms[X] contains two functions.
Consider the following PRP:
key space K={0,1}, PRP defined as:$\mathrm{E(k,x)=x\oplus k}$
Is this a secure PRP?
答案:Yes
当X = {0,1}下,随机置换如下:
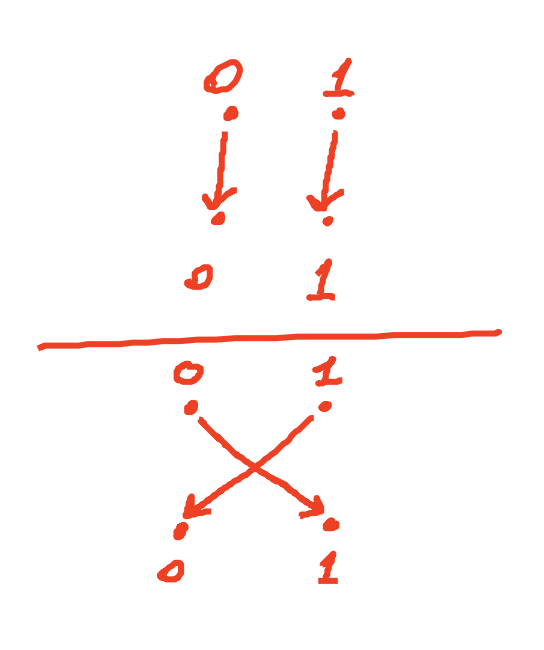
而选择K的分布和选择随机置换的分布相同,所以攻击者不能区分。
而如果问是否是secure PRF,答案则是:No。
攻击者可以定义这样一个统计算法,如果f(0)=f(1)则输出1,否则输出0。
则攻击者有 $\operatorname{Adv}_{\mathrm{PRF}}[\mathrm{A}, \mathrm{E}]:=|0-1/2|=1/2$ 的优势攻击成功。
现实中常见安全PRPs,有3DES, AES等,比如AES-128的置换是:$\mathrm{K\times X\rightarrow X}$ where $\mathrm{K=X={0,1}^{128}}$ 。
如果对AES的安全性定义的更具体,则是所有 $2^{80}$ 的算法A对AES攻击的优势 $\mathrm{Adv_{PRP}[A,AES]}<2^{-40}$ .
PRF Switching Lemma
Any Secure PRP is also a secure PRF, if |X| is sufficiently large.
【对于任意的安全PRP,当定义域 $X$ 足够大时,它也是安全PRF,所以AES也是安全的PRF。】
证明如下:
Lemma: Let E be a PRP over (K, X). Then for any q-query adversay A:
$$
|\mathrm{Adv_{PRF}[A,E]-\mathrm{Adv_{PRP}[A, E]}}|<\mathrm{q^2/2|X|}
$$
该引理的结果是,当 |X|很大时,$\mathrm{q^2/2|X|}$ 是neg.,因此左部分也是neg.。
而当E是安全PRP时,$\mathrm{Adv_{PRP}[A, E]}$ 是neg.,因此 $\mathrm{Adv_{PRF}[A,E]}$ 也是neg.,所以E也是安全的PRF。
证毕。
One Time Key
使用块密码有很多种方式,而我们的目的就是希望能从安全的PRP构建安全的加密方式。
本小节主要阐述one-time keys的方式,即每条消息都使用新的密钥,所以攻击者只能得到这一条有关该密钥的密文,即一次一密的唯密文攻击能力,但攻击者的攻击目标是希望能从密文中得到关于明文的信息,即破坏语义安全。
one-time key:
- Adversary’s power: Adv sees only one ciphertext (one-time key)
- Adversary’s goal: Learn info about PT from CT (semantic security)
在使用AES的ECB(Electronic Code Book)方式,当消息中的不同块 $\mathrm{m_1=m_2}$ 时,$\mathrm{c_1=c_2}$ ,攻击者能从密文中得到一些他不应该得到的信息。
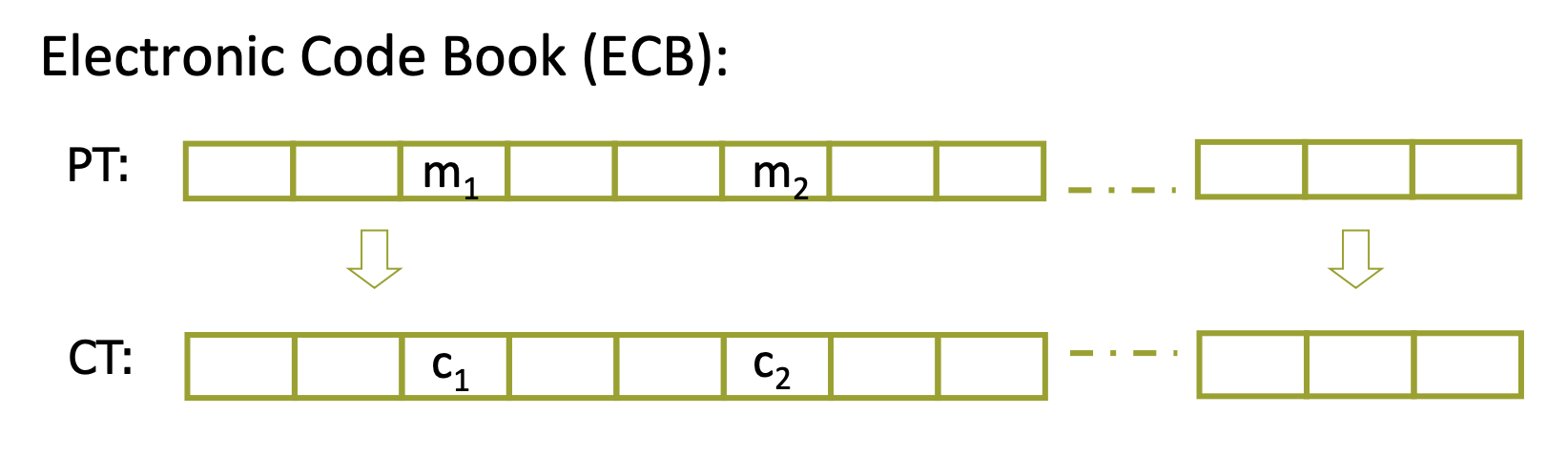
比如用ECB的方式加密图片,可以看到加密后的图片也是可见的:
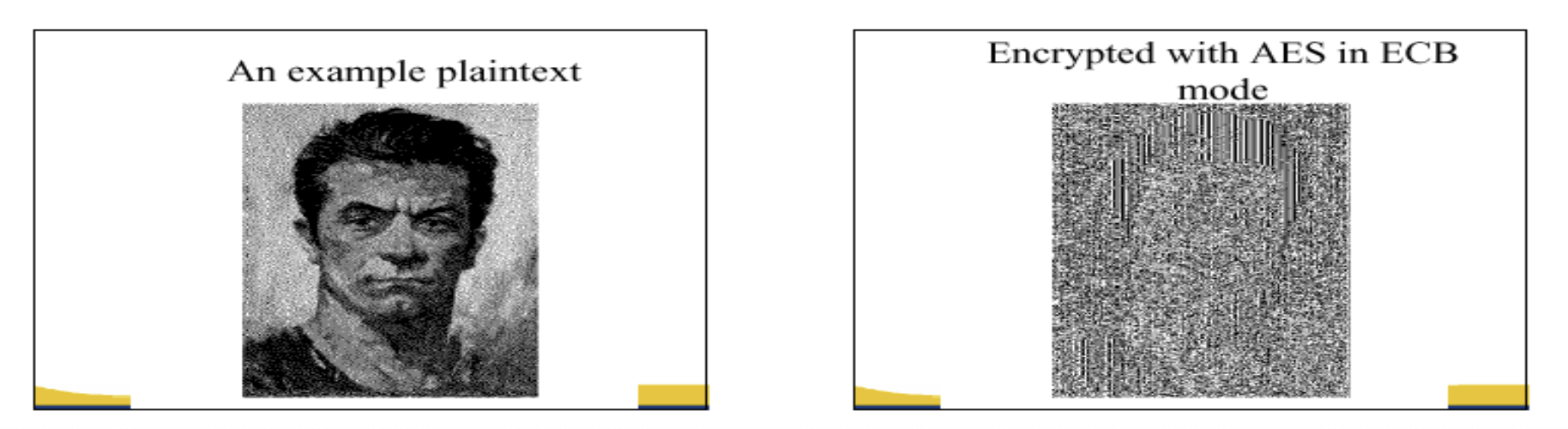
Semantic Security(one-time key)
这里的one-time key方式对于攻击者来说,就是攻击者只能看到一条与密钥相关的密文。
定义如下两个实验,挑战者随机选择一个密钥,以此确定用于加密的伪随机置换,攻击者发送任意两个消息 $\mathrm{m_0, m_1}$ ,长度相同。

在EXP(0)中,挑战者对 $\mathrm{m_0}$ 加密;而在EXP(1)中,挑战者对 $\mathrm{m_1}$ 加密。
攻击者收到挑战者响应的密文,通过一定的算法来判断该密文是对 $\mathrm{m_0}$ 加密的,还是对 $\mathrm{m_1}$ 加密的。
如果one-time key方式是语义安全的,则:
$$
\mathrm{Adv_{SS}[A,OTP]=|Pr[EXP(0)=1]-Pr[EXP(1)=1]} \quad \text{should be “neg”.}
$$
而我们上文提到的ECB,就不是语义安全的。
因为一条消息实则有许多块,而这些块中如果有相同的明文,则对应的密文相同。
攻击者可以利用这一点来区分 $\mathrm{m_0,m_1}$ :

攻击者可以用算法判断密文块是否相等来判断是对哪一条消息加密的。
该场景下, 攻击者攻击成功的优势为: $\mathrm{Adv_{SS}[A,ECB]}=|0-1|=1$ 。
Det. CTR
这里介绍一种从PRF构造的安全流密码:确定的计数器模式(Deterministic counter mode)
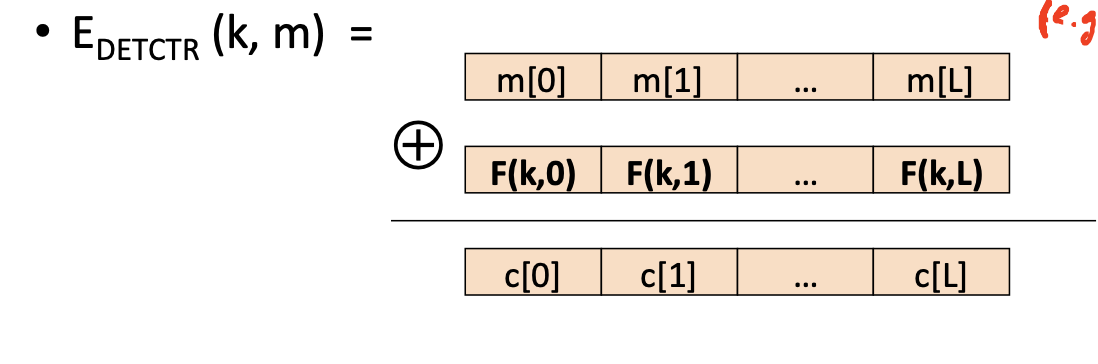
证明该种模式的安全性:
Theorem:
For any L>0, if F is a secure PRF over (K,X,X) then $\mathrm{E_{DETCTR}}$ is sem. sec. cipher over $\mathrm{(K,X^L,X^L)}$ .
In particular, for any eff. adversary A attacking $\mathrm{E_{DETCTR}}$ there exists an eff. PRF adversary B s.t.:
$$
\mathrm{Adv_{SS}[A,E_{DETCTR}]=2\cdot Adv_{PRF}[B,F]}
$$
该定理告诉我们,如果F是一个(K,X,X)上安全的PRF,那么 $\mathrm{E_{DETCTR}}$ 就是 $\mathrm{(K,X^L,X^L)}$ 上满足语义安全的密码(L是消息块数)。
此外,对于任意的有效攻击者A攻击 $\mathrm{E_{DETCTR}}$ 密码,都存在一个有效的PRF攻击者B攻击 $\mathrm{E_{DETCTR}}$ 底层的PRF,他们各自攻击的优势满足: $\mathrm{Adv_{SS}[A,E_{DETCTR}]=2\cdot Adv_{PRF}[B,F]}$ 。
当PRF是安全的PRF时,即 $\mathrm{Adv_{PRF}[B,F]}$ is negligible。因此,$\mathrm{Adv_{SS}[A,E_{DETCTR}]}$ 也必须是negligible的。
也可以通过下图直观的证明:
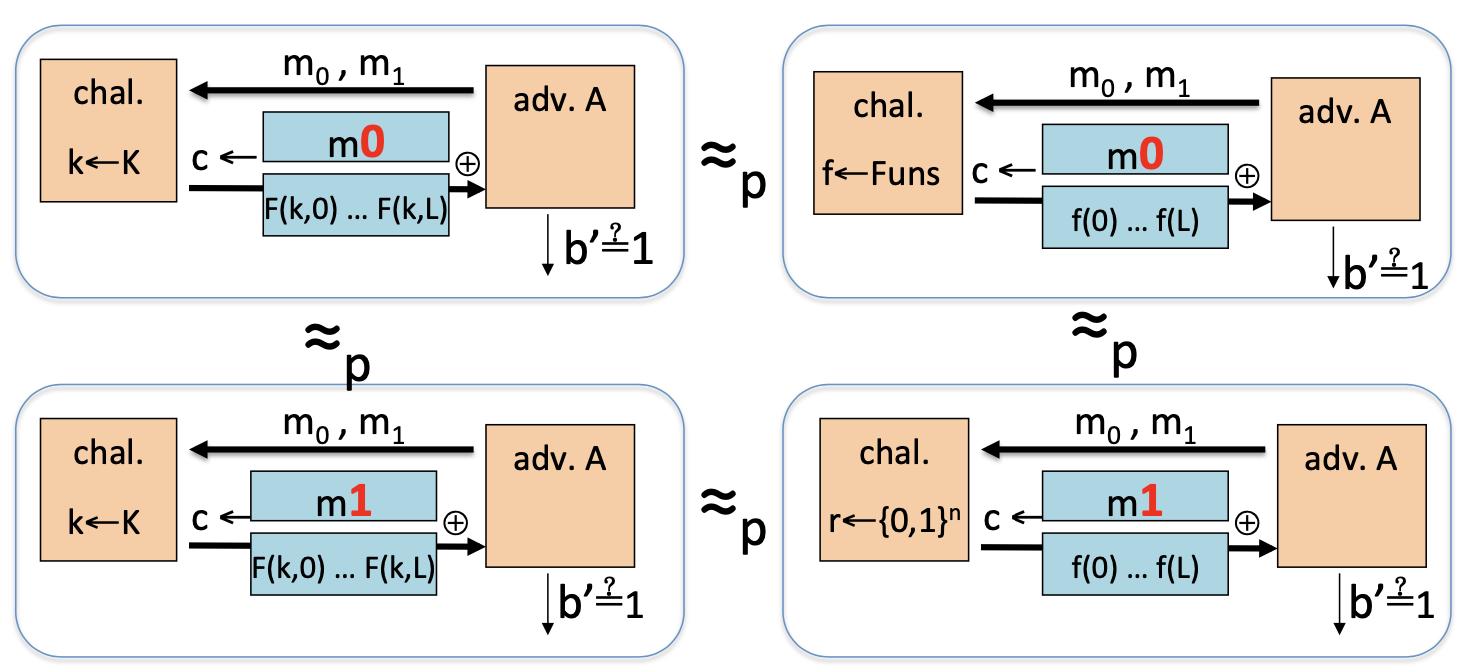
Many-time Key
块密码的另一种使用方式是many-time key方式,常用于文件系统,比如用同样的AES密钥加密许多文件;他也是IPsec的加密方式,相同的AES密钥用于加密许多IP包。
many-time key的方式是说,同一条密钥用于加密多条消息,在这种情况下,攻击者有选择明文攻击的能力,可以获得他任意选择明文消息对应的密文。而攻击者的目标同样是破坏语义安全。
many-time key:
- Adversary’s power: chosen-palintext attack(CPA): can obtain the encryption of arbitrary message of his choice.
- Adversary’s goal: break semantic security.
Semantic Security(many-time key)
挑战者随机选择密钥,以此确定加密解密密码。因为是many-time key的加密方式,攻击者可以发送多组消息:$\mathrm{m_{i,0},m_{i,1}}$ 。定义如下两个实验,对于攻击者发出的每一个询问中,在EXP(0)中,挑战者加密 $\mathrm{m_{i,0}}$ ,在EXP(1)中,挑战者加密 $\mathrm{m_{i,1}}$ 。攻击者对于收到的密文,来判断该密文是对 $\mathrm{m_{i,0},m_{i,1}}$ 那条消息加密的。

当攻击者想要指定明文 $\mathrm{m}$ 的密文时,攻击者可以向挑战者发出询问,询问中 $\mathrm{m_{j,0}=m_{j,1}=m}$ 。因此在many-time key的加密方式下,攻击者拥有选择明文攻击的能力。
定义many-time key 的语义安全:
Def: E is sem. sec. under CPA if for all “efficient” A:
$$
\mathrm{Adv_{CPA}[A,E]=|Pr[EXP(0)=1]-EXP(1)=1|}\quad \text{is neg.}
$$
CPA Security
如果 $\mathrm{E(k,m)}$ 对消息 $\mathrm{m}$ 总是输出相同的密文 $\mathrm{m}$ ,那该密码就不是语义安全的。
攻击过程如下图,攻击者在第一个询问发送 $\mathrm{m_0,m_0}$ ,得到 $\mathrm{m_0}$ 的密文,在第二询问中发送 $\mathrm{m_0,m_1}$ 。攻击者可以通过算法 A(output 0 if $\mathrm{c=c_0}$) 破坏其语义安全。

在现实生活中,这样确定的加密算法(deterministic encryption)都不能达到语义安全,比如一个攻击者可以通过两个加密文件的内容是相同的,来判断这两份文件时相同的。
所以,对于many-time key的加密方式来说,如果给定相同的密文消息,加密算法必须输出不同的密文,才能保证语义安全。
Solution 1: randomized encryption
第一种解决方案是 $\mathrm{E(k,m)}$ 是一个随机算法(randomized algorithm):
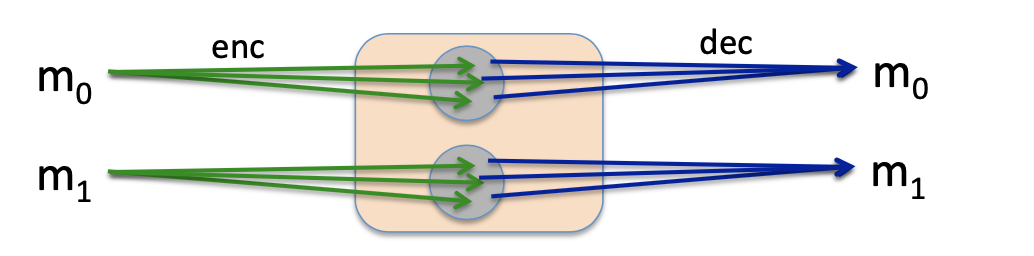
随机算法的好处是,每次加密相同的消息都能得到不同的密文。
但这样的性质需要满足,密文消息的长度比明文消息的长度长,即 CT-size = PT-size + #random bits
例如这样的加密算法:$\mathrm{F:K\times R \rightarrow M}$ 是一个安全的PRF,$\mathrm{E(k,m)=[r\stackrel{R}\longrightarrow, \text{output}(r, F(k,r)\oplus m)]}$ 就是一个在CPA攻击下语义安全的加密算法。(不过需要保证R的空间足够大,以此保证r不会重复)
Solution 2: nonce-based Encryption
第二种解决方案是基于nonce的加密算法。对于每一条消息nonce n都应该是不同的,即 $\mathrm{(k,n)}$ 不会重复。
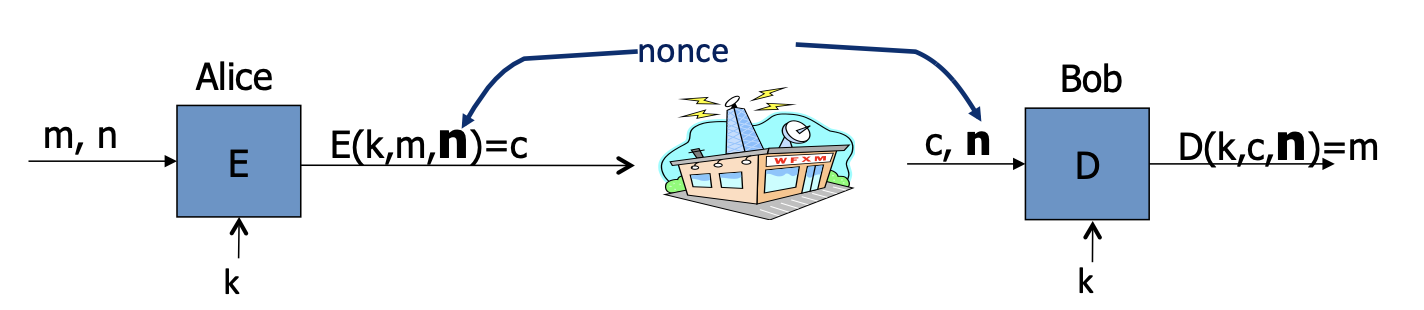
nonce可以是一个计数器(counter),也可以是一个随机值(random nonce)。
当nonce是攻击者选择时(每个询问的nonce都是不同的),系统保证语义安全的定义:
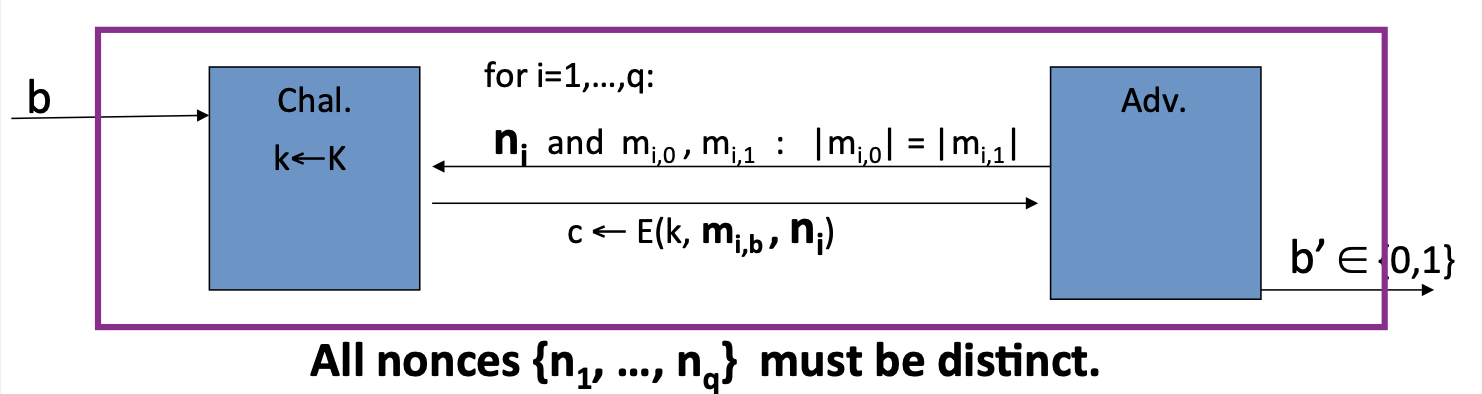
Def : nonce-based E is sem. sec. under CPA if for all “efficient” A:
$$
\mathrm{Adv_{nCPA}=|Pr[EXP(0)=1]-Pr[EXP(1)=1]|}\quad \text{is neg.}
$$
CBC
一种many-time key方式的块密码是CBC(Cipher Block Chaining)。
CBC with random IV
Let $\mathrm{(E,D)}$ be a PRP.
$\mathrm{E_{CBC}(k,m)}$ : choose random $\mathrm{IV\in X}$ and do:
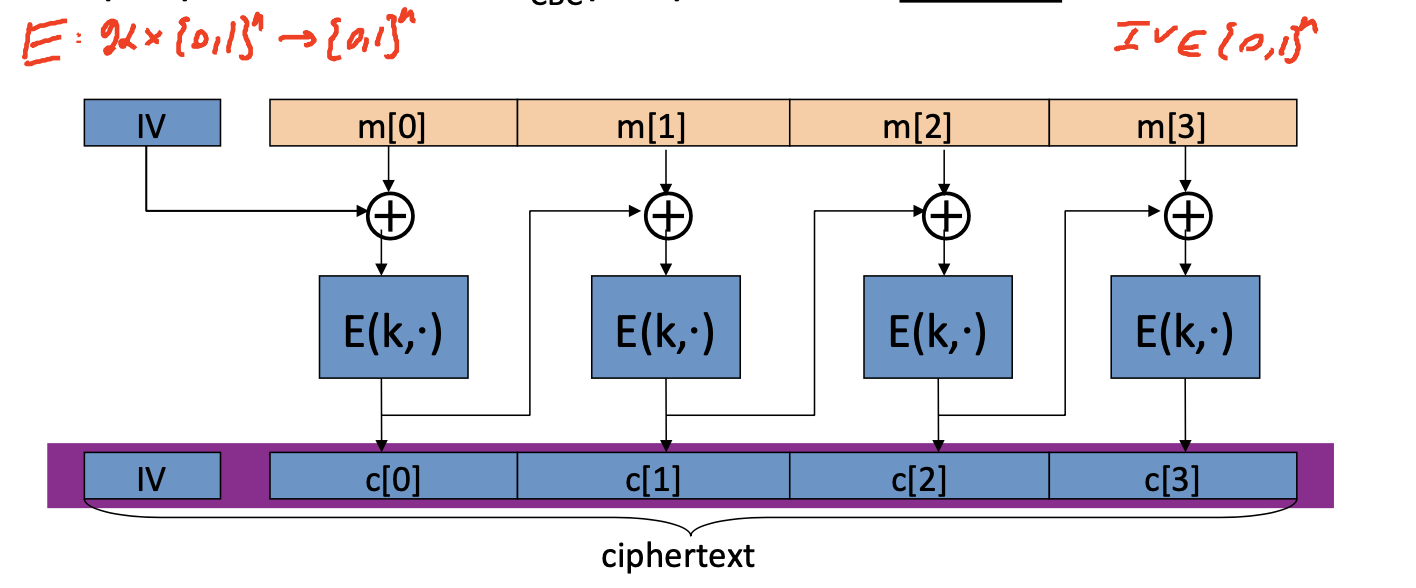
IV是随机的,因此要把IV的值放在密文中一起发送给解密方。
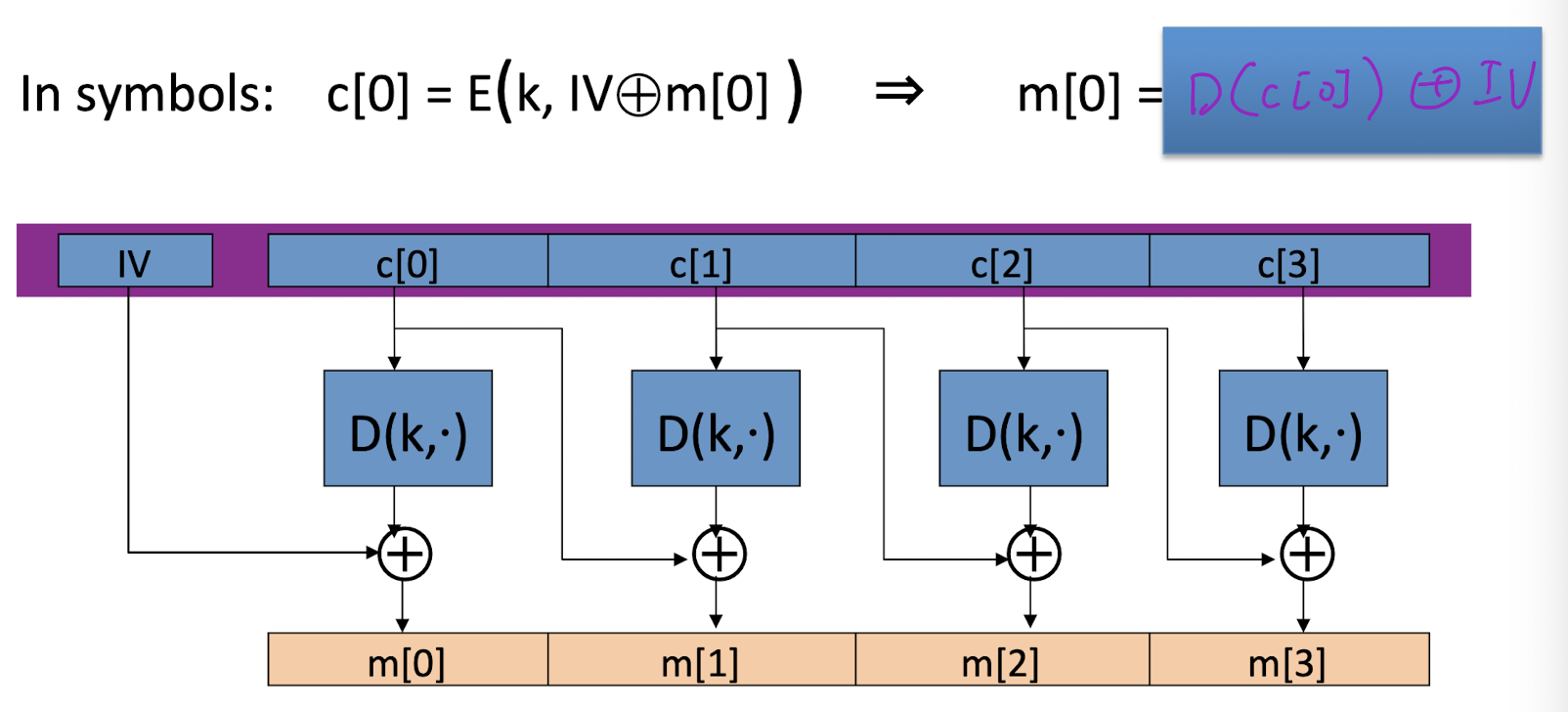
解密的电路如下:
CBC: CPA Analysis
定理:对于任意块 L>0(L就是每个消息能具备的最大块数),如果E在(K,X)上是一个安全的PRP,那么在CPA攻击下 $\mathrm{E_{CBC}} $ $\mathrm{=(K,X^L,X^{L+1})}$ 就是一个具备语义安全的密码。如果有一个攻击 $\mathrm{E_{CBC}}$ 的攻击者A,发起q个询问(q就是最大消息数),那么存在一个攻击其 PRP的攻击者B,满足:
$$
\mathrm{Adv_{CPA}[A,E_{CBC}]\le2\cdot Adv_{PRP}[B,E] +2q^2L^2/|X|}
$$
CBC Theorem:
For any L>0, if E is a secure PRP over (K,X) then $\mathrm{E_{CBC}} $ is a sem. sec. under CPA over $\mathrm{(K,X^L,X^{L+1})}$ .
In particular, for a q-query adversary A attacking $\mathrm{E_{CBC}} $ , there exists a PRP adversary B s.t.:
$$
\mathrm{Adv_{CPA}[A,E_{CBC}]\le2\cdot Adv_{PRP}[B,E] +2q^2L^2/|X|}
$$
q = # messages encrypted with k, L = length of max message
PRP是安全的,$\mathrm{ Adv_{PRP}[B,E]}$ 是neg.,因此只有当 $\mathrm{q^2L^2<<|X|}$ 时,CBC才是安全的。
Example:
假设我们希望 $\mathrm{Adv_{CPA}[A,E_{CBC}]}\le1/2^{32}$ ,即需要满足 $\mathrm{2q^2L^2/|X|\le1/2^{32}}$ :
对于AES来说,$\mathrm{|X|=2^{128}}$ ,所以 $\mathrm{qL\lt 2^{48}}$ 。
因此,在 $2^{48}$ 个AES块后,必须改变密钥。
而对于DES来说,$\mathrm{|X|=2^{64}}$ ,所以 $\mathrm{qL\lt 2^{16}}$ 。
Warning: an attack on CBC with random IV
当攻击者可以预测IV时,CBC就不再具备CPA-secure了。
假设攻击者对于给定的密文$\mathrm{c\leftarrow E_{CBC}(k,m)}$可以预测下一条消息的IV。
比如在SSL/TLS1.1中的一个bug:第i-1条报文的最后一个密文块就是第i条报文的IV。
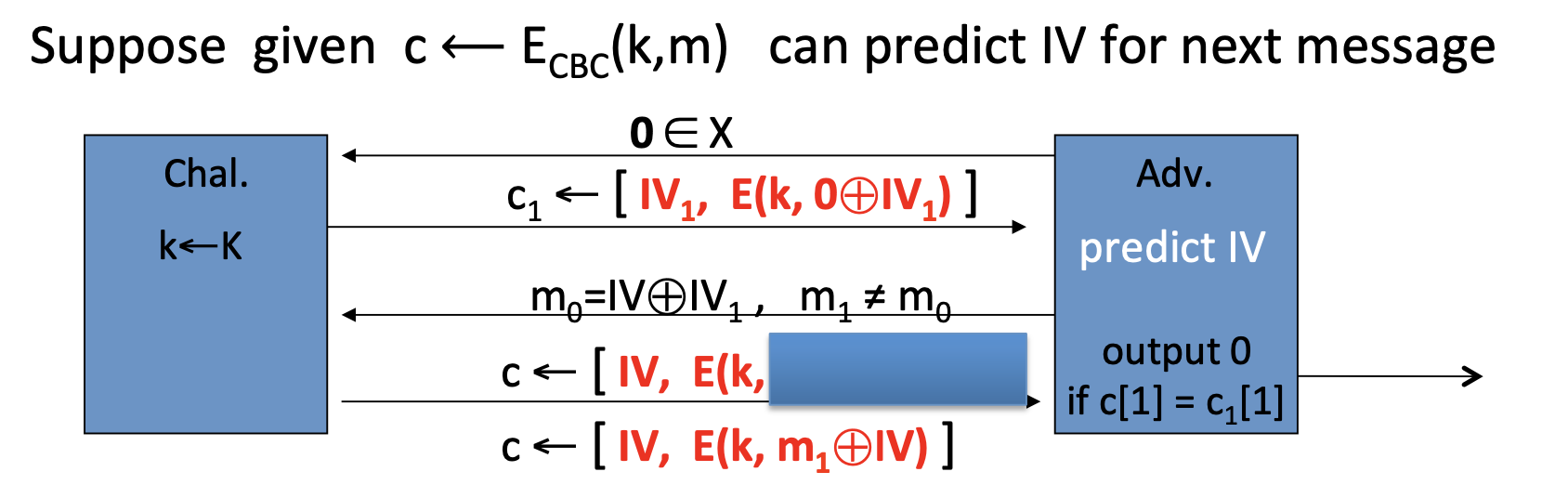
CPA attack:
- 第一次询问
- 攻击者发送两条消息 $\mathrm{m_0=m_1=0}\in \mathrm{X}$
- 挑战者用 $\mathrm{c_1=[IV_1, E(k,0\oplus IV_1)]}$ 响应
- 攻击者通过密文预测下一条消息的IV
- 第二次询问
- 攻击者发送两条消息 $\mathrm{m_0=IV\oplus IV_1,m_1\ne m_0}$
- 挑战者的密文 $\mathrm{c=[IV,E(k,IV_1)]\quad or \quad c=[IV,E(k, m_1\oplus IV)]}$
- 攻击者的统计算法 A: output 0 if $\mathrm{c[1]=c_1[1]}$
所以IV必须是随机的。
nonce-based CBC
CBC的另一种使用方式是基于unique nonce。
在这种方式中,密钥由一组密钥对组成 key = (k, k1),k1是用来加密nonce的。
unique nonce的含义是,nonce可以不是随机的,但对于每一条消息,(key, nonce)对都必须是不同的。
所以,对于用户提供的非随机nonce,必须经过加密。
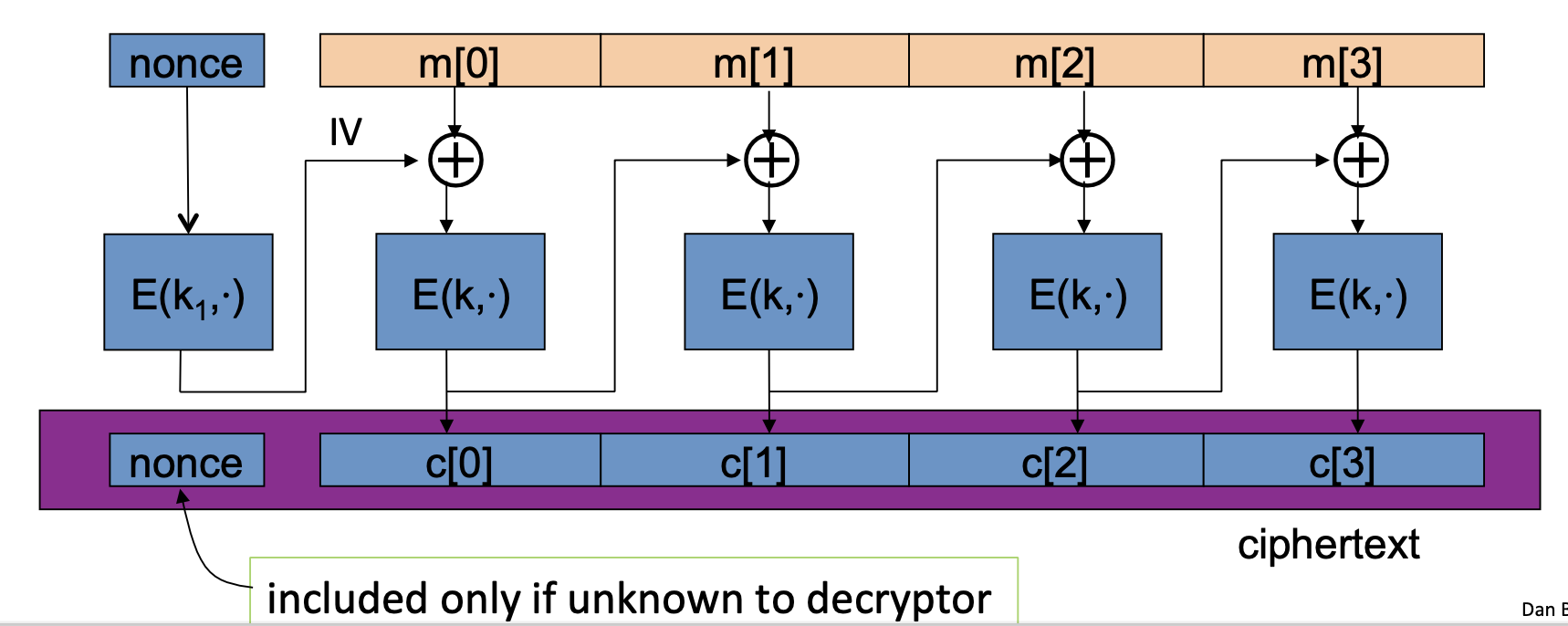
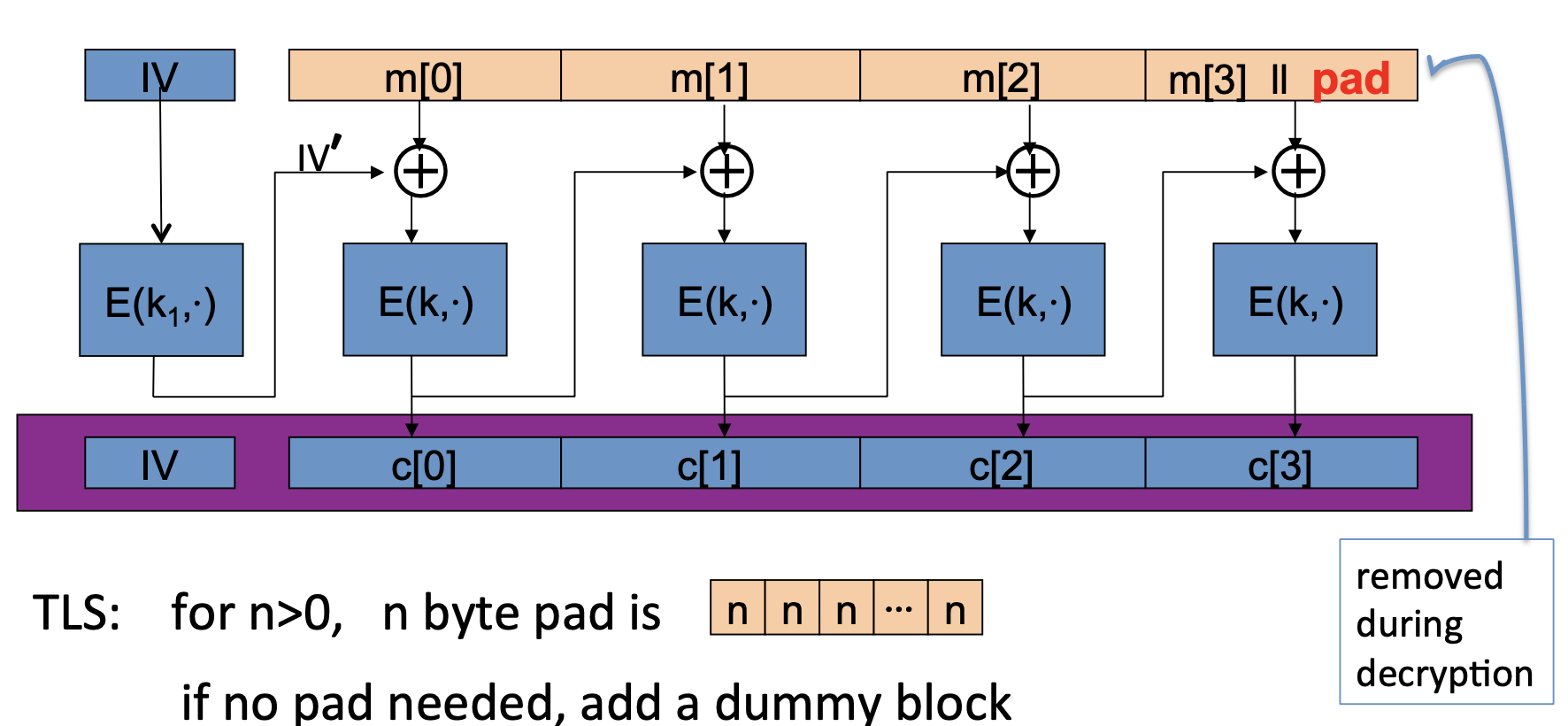
在这种方式中,一个非常重要但步骤就是使用 k1来加密nonce。
如果把nonce当作IV使用(忘掉k1加密nonce的步骤),CBC就没有CPA-secure。
如果k1=k,CBC也没有CPA-secure(IV=0的模式)。
A CBC technicality: padding
对于消息长度未能达到块的整数倍,需要padding技术进行填充消息。

在TLS中的填充方法是,对于需要填充n(n>0)个bytes的消息块,n-byte pad中的每个字节都是n。
如果不需要填充,就需要添加一个dummy block,该块中的每个字节都是16。
CTR
另一种方式是CTR。
rand ctr-mode
Let F be a secure PRF.
$\mathrm{E_{CBC}(k,m)}$ : choose random $\mathrm{IV\in X}$ and do:

CTR模式的最大优点是可以并行计算。
其次,因为CTR的加密其实是流密码的形式,所以只需要要求F是一个安全的PRF,不需要其可逆。
nonce ctr-mode
为例保证F(k,x)只会使用一次,对每条消息选择一个64 bits的nonce,同时使用一个64 bits的counter。

CTR: CPA analysis
CTR Theorem:
For any L>0, if F is a secure PRF over (K, X, X) then $\mathrm{E_{CTR}} $ is a sem. sec. under CPA over $\mathrm{(K,X^L,X^{L+1})}$ .
In particular, for a q-query adversary A attacking $\mathrm{E_{CTR}} $ , there exists a PRF adversary B s.t.:
$$
\mathrm{Adv_{CPA}[A,E_{CTR}]\le2\cdot Adv_{PRF}[B,F] +2q^2L/|X|}
$$
q = # messages encrypted with k, L = length of max message
CTR-mode中,只有当 $\mathrm{q^2L}<<|X|$ ,才具备CPA-secure,比CBC好。
Example:
假设我们希望 $\mathrm{Adv_{CPA}[A,E_{CTR}]}\le1/2^{32}$ ,即需要满足 $\mathrm{2q^2L/|X|\le1/2^{32}}$ :
对于AES来说,$\mathrm{|X|=2^{128}}$ ,所以 $\mathrm{qL^{1/2}\lt 2^{48}}$ 。
因此,在 $2^{32}$ 条消息后(每条消息有 $2^{32}$个 AES块),必须改变密钥。
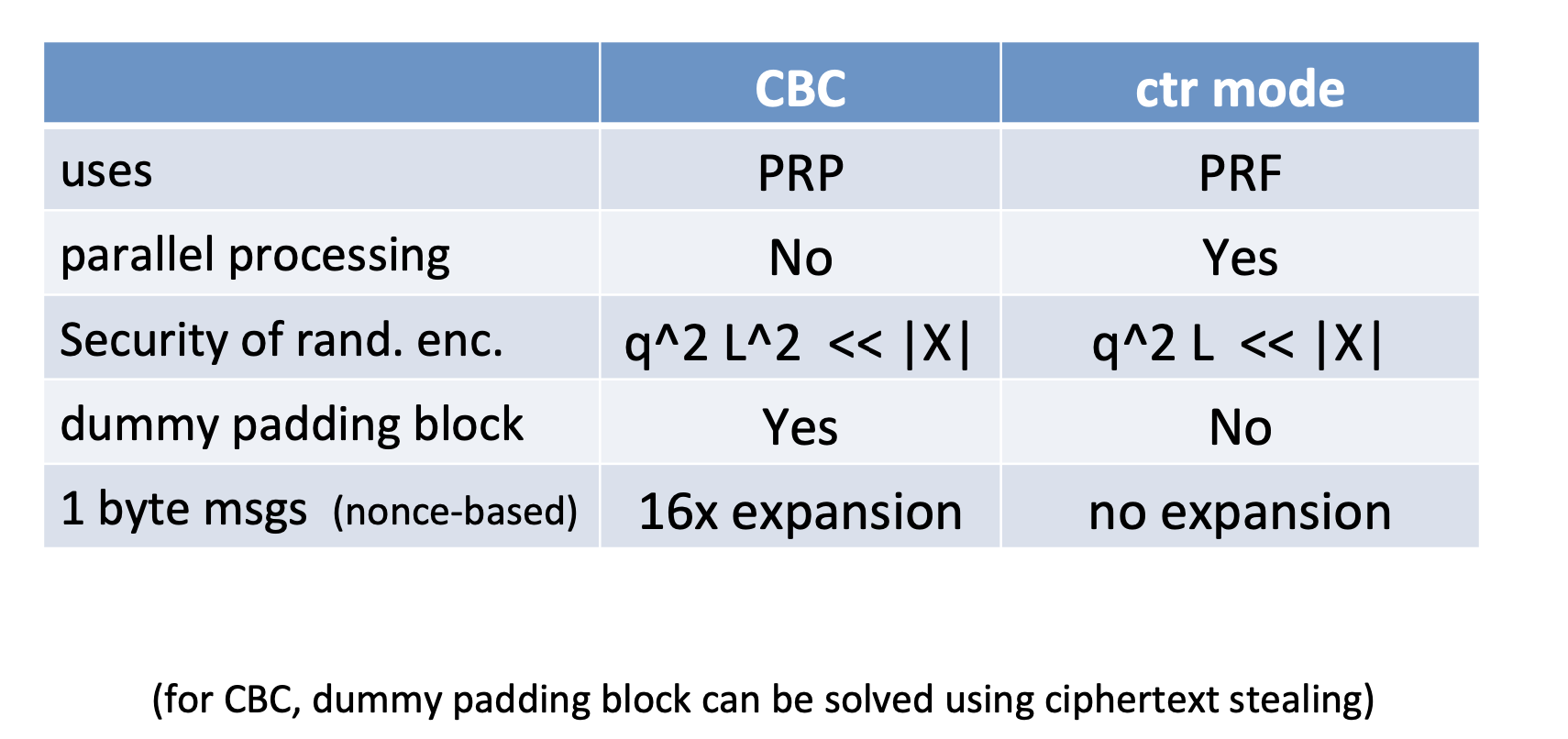
CTR v.s. CBC
「Cryptography-Boneh」:Block Cipher 2

