「MPC-Mike Rosulek 」:Advanced Techniques and Optimizations for Garbled Circuits
本系列是总结Mike Rosulek教授在上海期智研究院的密码学学术讲座。
这是Mike教授的第二个分享:Advanced Techniques and Optimizations for Garbled Circuits
Roadmap
- Optimizations: How did garbled boolean circuits get so small?
- New frontiers: How to garble arithmetic circuits?
在这篇文章中,会介绍在garble boolean circuits时的优化技术:包括point-and-permute, row-reduction, free-XOR和half gates。此外,这篇文章还会介绍如何garble arithmetic circuits。
Optimizing garbled circuits
在上一篇文章中,介绍了garbled circuits的核心思想:
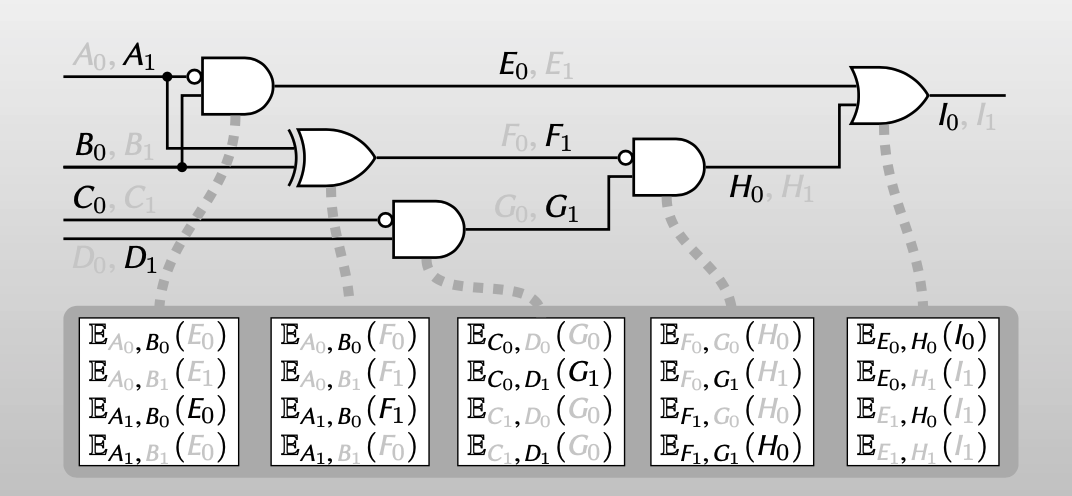
Given garbled gate + one wire label per input wire:
- can learn only one output label (authenticity)
- cannot learn truth value of labels (privacy)
garbled circuits的计算性能和速度主要取决于他的大小(ciphertext的数量),但现实中garbled circuits的计算是非常快的。
因为现有的garbled boolean circuits使用了一些优化技术,使得garbled gate的ciphertext表示数量大幅下降。
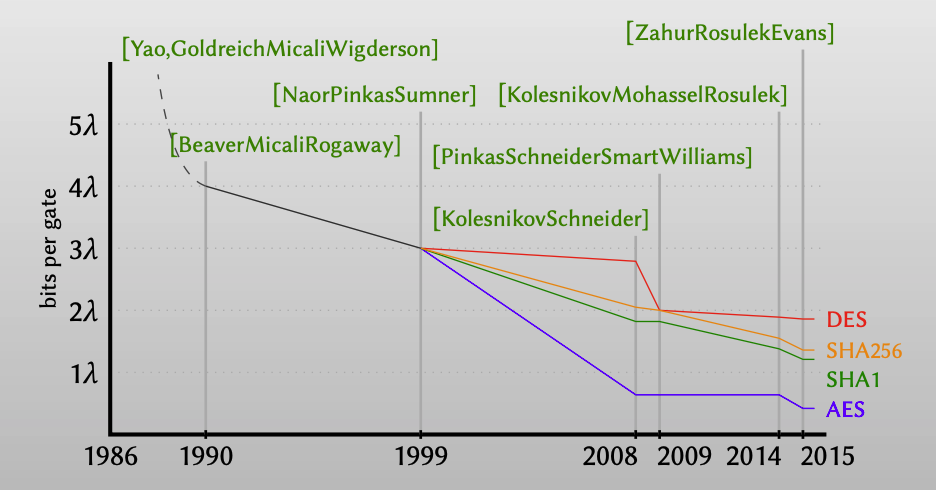
Ciphertext expansion
在介绍这些优化技术之前,我们先来分析Yao’s protocol中garbled circuits的大小。
每个boolean gate的wire有两种输入(0或者1),对每个输入都随机选择一个label,再用对应的label(密钥)对输出加密,得到下图的garbled gates(ciphertext)。
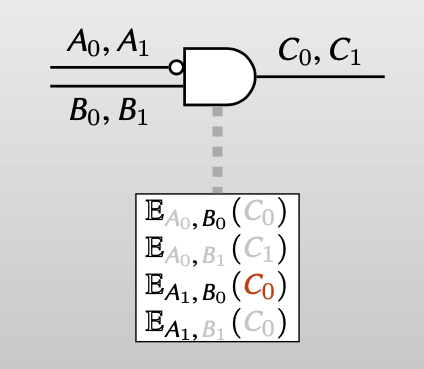
但是这样的排列方式会泄漏语意信息,因此需要打乱ciphertext的顺序。
而evaluator在evaluate时,只能用得到的labels一个一个尝试性解密。
为了让evaluator在解密时能清楚知道解密出的label是正确的,就需要使用带有ciphertext expansion的加密方案。(比如在加密时,如果label是4位的,可以通过在label前加4个前导0)这样得到的garbled gate的ciphertext长度是原label长度的一倍。
Point-and-permute
首先介绍的是Point-and-permute技术:
Assign color bits red & blue to wire labels.
Association between (red, blue ) <-> (True, Flase) is random for each wire.
【color bits 可以看作是一个bit mask,或者说是一个1-bit one-time pad。在为每一个wire的labels分配color bits时,是随机分配的:随机选择一个bit r (0或者1),对于wire a,label的color bits的计算是 $a\oplus r$ 。】
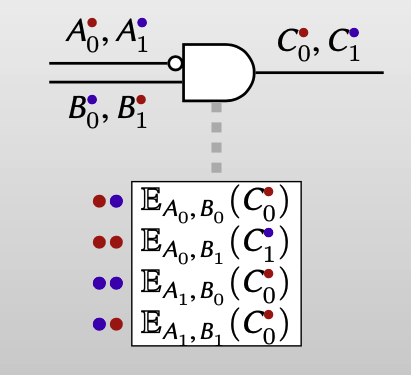
A wire label reveals its own color(e.g. as last bit)
【可以在label后再附加一个bit作为color bit,来表示该wire label的颜色】
Order the 4 ciphertexts canonically, by color of keys.
【然后对表示garbled gate的4个ciphertexts按照指定的颜色组合排序】
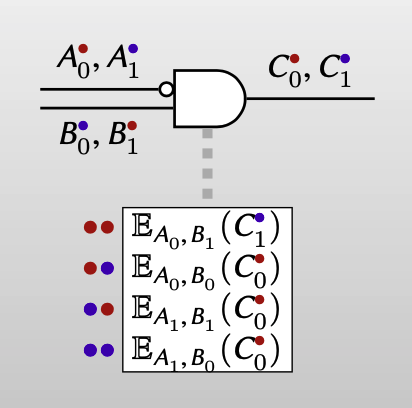
Evaluate by decrypting ciphertext indexed by your colors
【这样evaluator在evaluate混淆电路时,就可以通过已知labels的颜色组合索引出正确的密文,再进行解密,不再需要对每一个密文进行尝试性解密。】
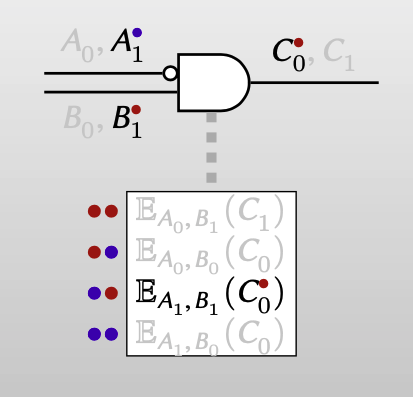
通过Point-and-permute技术,evaluator在评估电路时不再需要对每个密文尝试性解密,garbler在混淆电路时也不再需要做ciphertext expansion。
同时,该技术支持简单的one-time pad加密,即 $\mathbb{E}_{A, B}(C)=H(A, B)\oplus C$ ,$H$ 可以是任意的一种加密方式,比如AES。
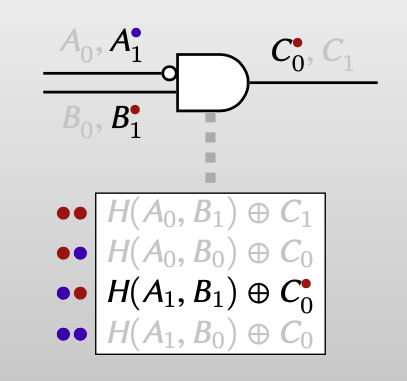
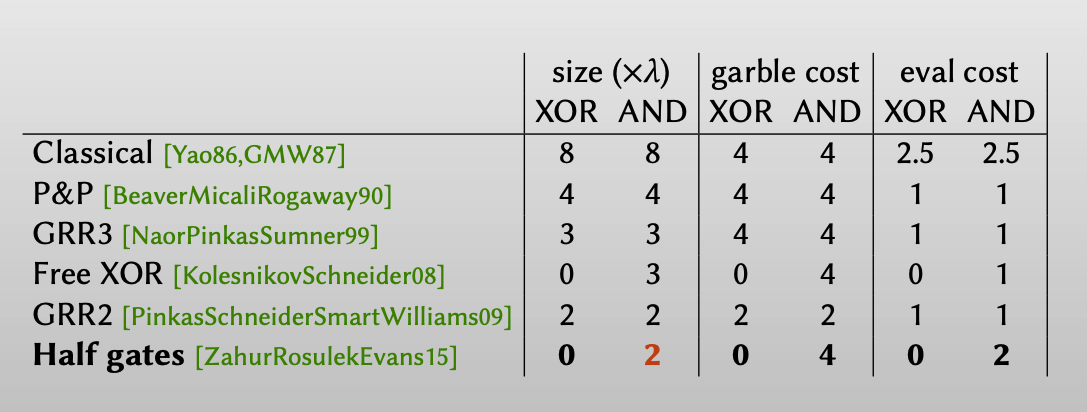
我们将Point-and-permute与Yao’s protocol进行比较:

- 假定单个label大小是 $\lambda$ ,garbled circuits的大小表示为ciphertexts的大小 。garble cost的值代表garbler加密时的开销,eval cost的值表示evaluator解密时的开销。
- 对于Yao的方案,因为有ciphertext expansion,所以garbled circuits的大小为 $8\lambda$ 。对每个garbled gate,都需要生成4个ciphertexts。而evaluator在评估电路时,每个ciphertext都有 1/4的概率是正确的,所以开销为 $2.5 = 1\times 1/4 + 2 \times 1/4 + 3\times 1/4 + 4\times 1/4$ .
- 对于Point-and-permute的方案,不需要ciphertext expansion,所以garbled circuits的大小为 $4\lambda$ 。在evaluator评估电路时,可以通过labels的颜色组合来索引密文,因此只需要1的开销。
Garbled Row Reduction
Row Reduction[NaorPinkasSumner99] 是在Point-and-permute方案上进一步优化:
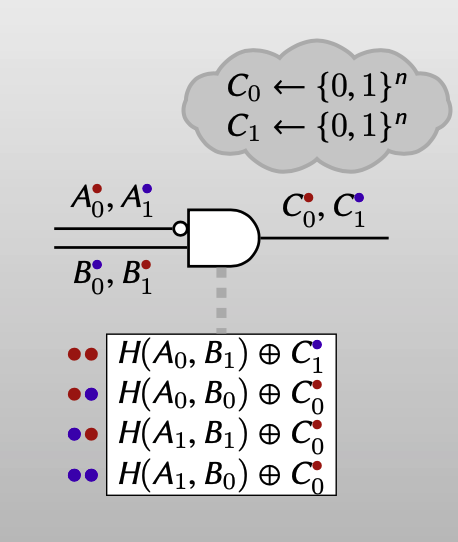
相较于Point-and-permute方案中的随机生成输出wire的labels,Row Reduction方案在输出wire的labels生成中,使用了一个trick:label $C_0$ 随机生成,而label $C_1$ 是一个能让P&P方案中的第一个ciphertext为 $0^n$ ,即 $C_1 = H(A_0, B_1)$ 。虽然$C_1 = H(A_0, B_1)$ ,但对除garbler以外的人来说,$C_1$ 和random bits是不可区分的,即 $C_1$ 看起来和随机生成的label一样。

对garbler来说,每个garbled gate就可以只用3个ciphertexts表示。
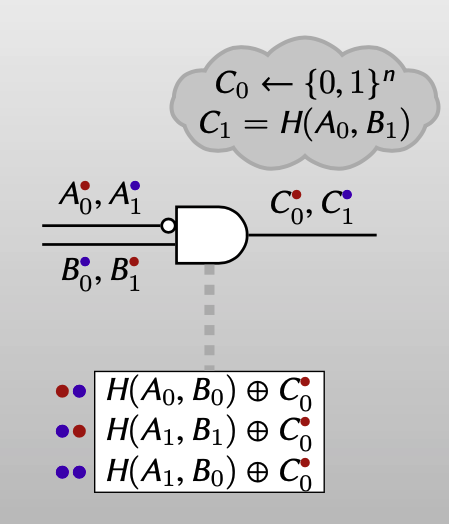
但对evaluator来说,他只需要把 $0^n$ 加上,重构为4个ciphertexts,后面的操作和P&P方案相同。
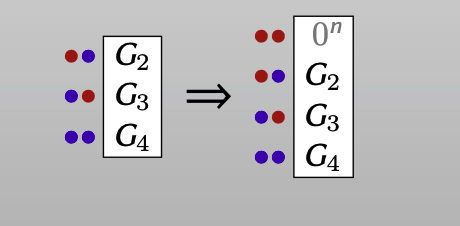
同样的,我们把Row Reduction的方案和前两种方案进行比较:

GRR3方案相对于P&P方案,可以将garbled circuits的数量从4降为3。
Free XOR
Free XOR[KolesnikovSchneider08] 是对异或门的优化技术。
Define offset of a wire ≡ XOR of its two labels
【Free XOR对wire定义了一种offset $\Delta$ ,该值其实等于两个labels的异或】
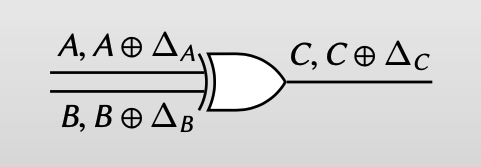
Choose all wires in circuit to have same (secret) offset ∆
【Free XOR方案中,对所有的wires都选择了一个相同的保密的offset】
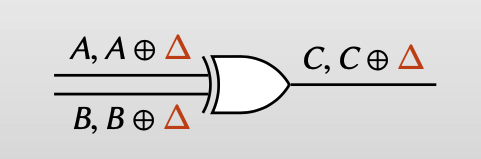
Choose false output = false input ⊕ false input
【相较于之前方案的随机生成output wire的label,Free XOR让output wire的false output = false input ⊕ false input】
【也就是令 $C = A \oplus B$ (A: false , B: false, C: false)】
Evaluate by xoring input wire labels (no crypto)
【如此定义output wire的label,output wire的label可以通过input wire的label直接计算出来,而不需要再对其加密解密】
【false xor false = false | $A \oplus B = C$ 】
【false xor true = true | $A \oplus B \oplus \Delta = C\oplus \Delta$ 】
【true xor false = true | $A \oplus \Delta \oplus B = C\oplus \Delta$ 】
【true xor true = false | $A \oplus \Delta \oplus B \oplus \Delta = C$ 】
同样,我们把XOR的方案和之前方案比较,由于XOR方案只适用于XOR gate,因此把XOR gate和AND gate分开:

Row reduction $\times$ 2
Row reduction $\times$ 2[GueronLindellNofPinkas15] 方案是对Row Reduction方案的进一步优化,Row Reduction方案对输出wire的label选择上:$C_0$ 随机生成,$C_1$ 的值是能让P&P方案第一个ciphertext 为 $0^n$ 的方案,即 $C_1 = H(A_0, B_1)$ (式子只是针对下图的样例)。
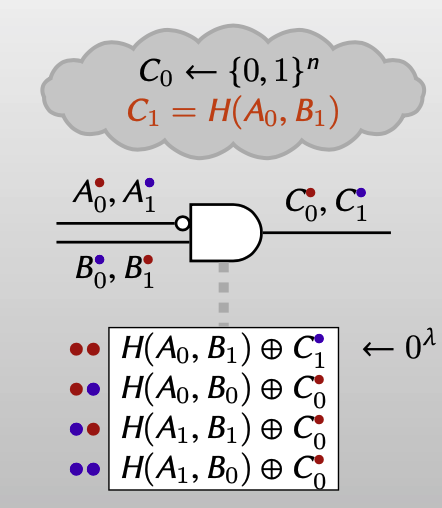
而Row reduction $\times$ 2方案规定label $C_0 = H_{00}\oplus H_{11} \oplus H_{10}$ ,这样能让剩下三个ciphertext的XOR值为 $0^n$ ,同样的 $C_0$ 对除garbler之外的人来说和random bits不可区分。
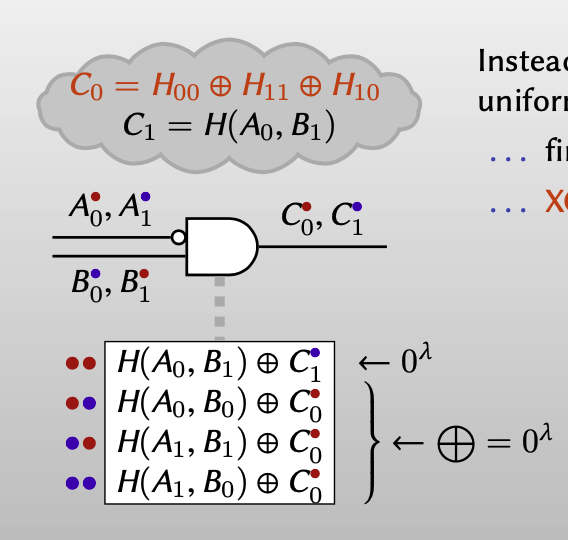
因此,对garbler来说,每一个garbled gate只需要用两个ciphertexts表示:
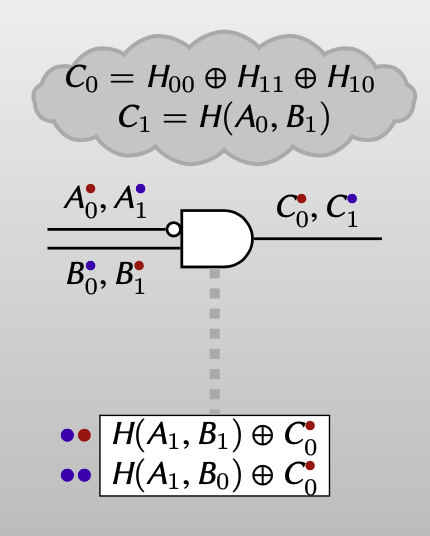
而对evaluator来说,他只需要用这两个ciphertexts重构出原本的garbled circuits即可:
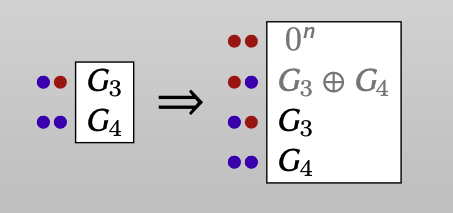
同样,把GRR2方案和其他方案比较,主要和P&P和GRR3方案比较,每个garbled gate都只需要用两个ciphertexts即可表示:
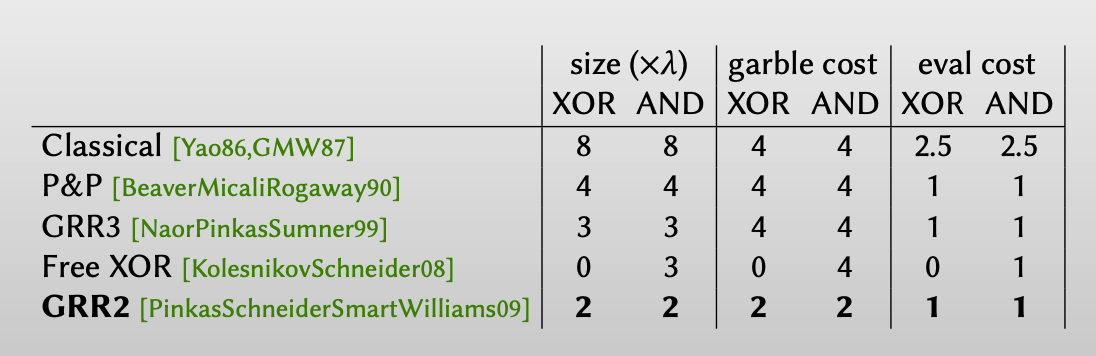
这里需要注意的是,Free XOR技术和GRR2技术是不可兼容的。因为在GRR2中,$C_0 = H_{00}\oplus H_{11} \oplus H_{10}$ ,$C_1 = H(A_0, B_1)$ ,无法保证 $C_0\oplus C_1=\Delta$ 。因此在一个电路中,那么使用Free-XOR方案,要么使用GRR2方案。
Half Gates
Half Gates 方案出自Samee Zahur, Mike Rosulek, David Evans的15年的文章:Two Halves Make a Whole: Reducing Data Transfer in Garbled Circuits using Half Gates. (Eurocrypt 2015)
这个方案garbled circuits的设计是借用了Free-XOR的部分设计:即所有的wire都选择了一个相同的offset。但output wire label $C$与input wire的label无关。
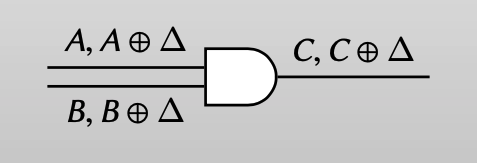
Garbler: half gate
如果garbler提前知道了input wire a的值:
$a = 0$
如果$a = 0$, 这个门就变成一个一元门: $b \rightarrow 0$
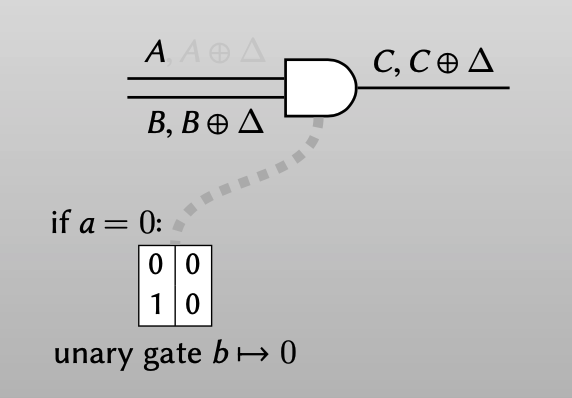
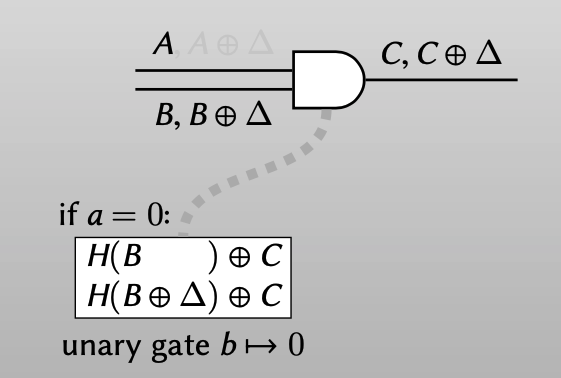
可以用2个ciphertexts来表示这个门,evaluator解密后都得到output wire 的label $C$。

$a = 1$
如果$a = 1$, 这个门就变成一个一元门:$b\rightarrow b$
同样可以用2个ciphertexts表示这个门,evaluator可以用label $B$解密得到output wire 的 label $C$,可以用 label$B\oplus \Delta$ 解密得到output wire 的label $C\oplus \Delta$ 。
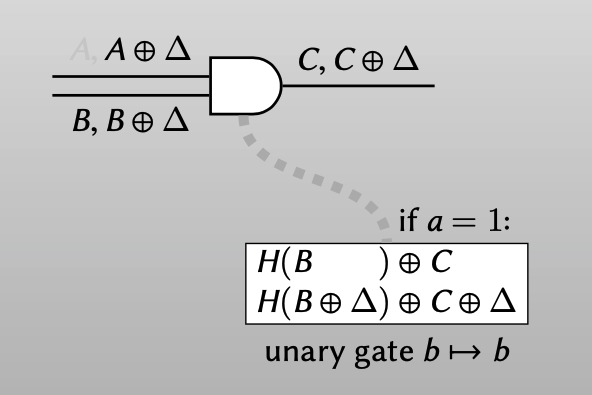
结合两种情况:
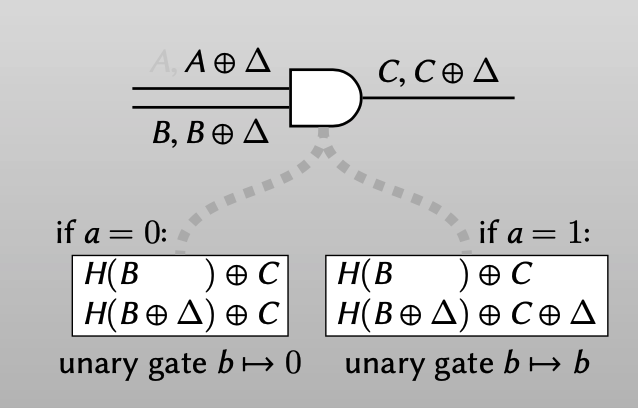
可以归纳为下式,garbler可以根据已知a的值来生成对应的ciphertexts,同样用point-and-permute的color bit的思想来重排列ciphertexts。
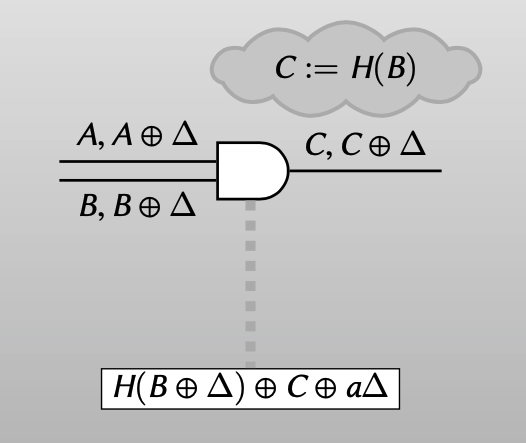
同样,也可以再用row reduction的技术来选择output wire的false label $C=H(B)$ ,使得第一个ciphertext为 $0^n$ ,这样对于garbler知道一个input wire真值的garbled half gate就可以用一个ciphertext来表示:
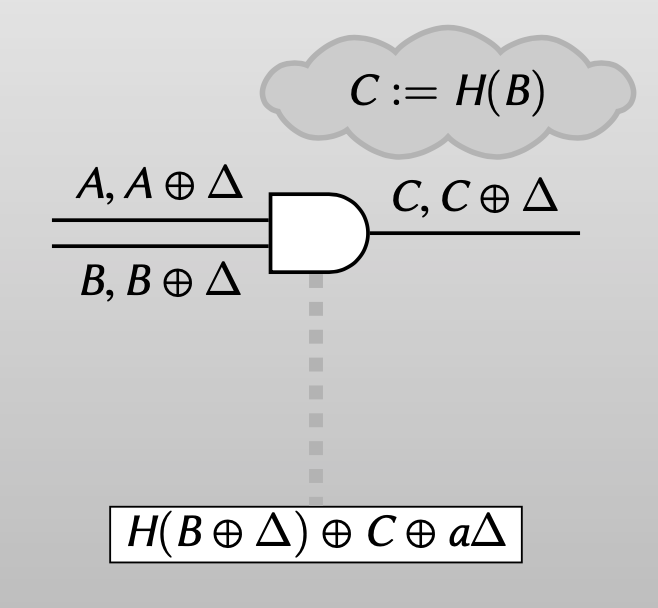
Evaluator: half gate
如果evaluator提前知道了input wire b的值,即知道label的对应真值:
Evaluator has B (knows label B is false): should obtain C (false)
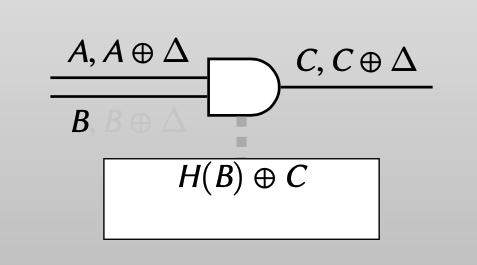
Evaluator has $B\oplus \Delta$ (knows label $B\oplus \Delta$ is true): should be able to transfer truth value from “a” wire to “c” wire.
【即如果evaluator知道wire b的label是true,那evaluate的结果的真值应该和wire a上label对应的真值相同(即使她不知道wire a上实际的真值是什么)】
Evaluator只要知道 $A\oplus C$ 的值,就可以实现 “transfer truth value from “a” wire to “c” wire.”
false($A$) -> false ($C$) : $A\oplus A \oplus C = C$
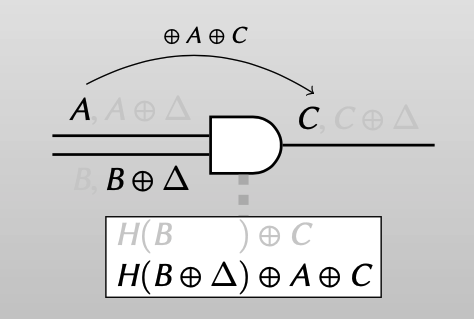
true($A\oplus \Delta$ )-> true ($C\oplus \Delta$ ): $A\oplus \Delta \oplus A \oplus C = C\oplus \Delta$
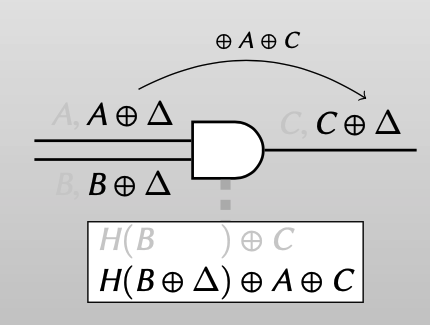
同样的,可以使用row reduction的技术,令false label $C = H(B)$ ,使得garbled circuits的第一个ciphertext为 $0^n$ ,这样对于evaluator知道一个input wire真值的garbled half gate就可以用一个ciphertext表示。
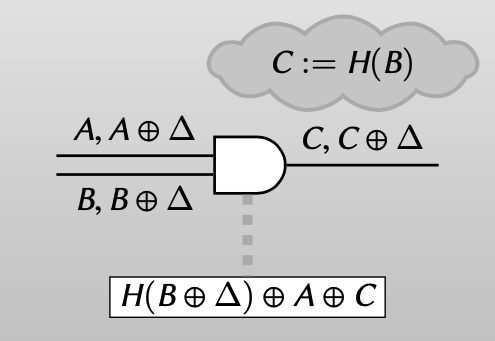
Two halves make a whole
对于在复杂电路中的AND门,他的input wire可能和双方输入都相关,因此garbler不知道某个input wire的真值到底是什么,evaluator更不知道。
如何才能将上文中的half gate应用到一般AND门上?
对于garbler来说,在garble AND gate时,即然不知道某个inpu wire的真值,那我们可以引入一个随机bit r(0或者1),该值其实就是在计算label的color bit时引入的,而bit $a\oplus r$ 就是label $A$ 的color bit。
- 对于garbler来说,garbler知道bit $r$的真值,true or false。
- 对于evaluator来说,他在evaluate这个AND gate时,他会得到wire a的label,虽然不知道这个label实际是对应着true还是false(即不知道 $a$ 的值),但是他知道这个label的color bit是什么(像P&P中提到的那样,可以把color bit放在label的最后一位),而这个color bit其实就是bit $a\oplus r$ 的真值,所以evaluator在evaluate时是知道 bit $a\oplus r$ 的真值的。
现在我们通过引入了 bit $r$ ,实现了half gate的两个假设,一个是让garbler知道AND gate其中一个的输入真值,一个是让evaluator知道AND gate其中一个的输入真值。
那如何通过 bit $r$ ,把一个一般AND gate转变为half gates 呢?
把 $a\wedge b$ 写成如下式:
$$
\begin{align}
a\wedge b &= (a\oplus r \oplus r)\wedge b \
&=[(a\oplus r)\wedge b]\oplus [r\wedge b]
\end{align}
$$
- 对于左边的 $[(a\oplus r)\wedge b]$ :evaluator知道 $a\oplus r$ 的真值,可以用上面提到的第二种half gate。
- 对于右边的 $[r\wedge b]$ : garbler知道 $r$ 的真值,可以用上面提到的第一种 half gate。
- 两个式子的xor运算:就可以使用Free-XOR 技术。
因此,总开销 = 2 “half gates” + “1 XOR gate” = 2 ciphertexts
同样的,把Half gates的方案和其他技术进行比较,AND gate的大小可以降为2,同时Half gates技术和Free-XOR技术是兼容的,因此在half gates方案中,XOR gate的开销为0.
Garbling arithmetic circuits
Generalized Free XOR
将Free XOR的思想迁移到 $\mathbb{Z}_m$ 上。
| Free XOR | Gerneralized Free XOR |
|---|---|
| Wire carries a truth value from ${0, 1}$ | Wire carries a truth value from $\mathbb{Z}_m$ |
| Wire labels are bit strings ${0, 1}^\lambda$ . | Wire labels are tuples $(\mathbb{Z}_m)^\lambda$. |
| Global wire-label-offset $\Delta\in{0, 1}^\lambda$ | Global wire-label-offset $\Delta\in(\mathbb{Z}_m)^\lambda$ |
| false wire labe lis $A$ ;true wire label is $A\oplus \Delta$ | Wire label encoding truth value $a\in \mathbb{Z}_m$ is $A+a\Delta$ |
| ⊕ is componentwise addition mod 2 | + is componentwise addition mod m |
Generalized Free XOR的核心就是:用wire label $A+a\Delta\in (\mathbb{Z}_m)^\lambda$ 来编码 $a\in \mathbb{Z}_m$ 。
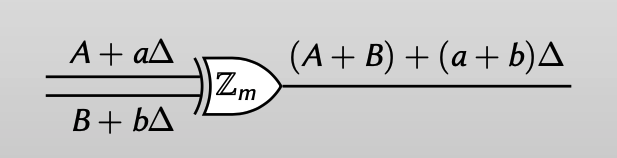
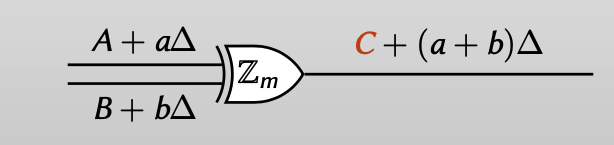
这样编码后,evaluator可以直接通过对label进行模 $m$ 的加法操作来完成evaluate:
Garbling unary gates
一元门 $\phi$ (unary gates): 只有一个input wire $\in \mathbb{Z}_m$, 一个output wire $\in \mathbb{Z}_l$,注意两个wire可以属于不同的有限域。
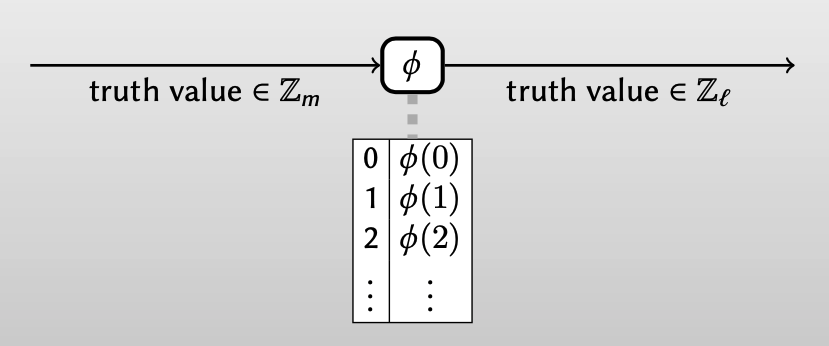
Generalized Free XOR除了可以混淆模 $m$的加法电路,还可以混淆一元门。
用input wire label $A+a\Delta_m\in (\mathbb{Z}_m)^\lambda$ 来编码 $a\in \mathbb{Z}_m$ ,用output wire label $C+a\Delta_l \in (\mathbb{Z}_l)^\lambda$ 来编码 $c\in \mathbb{Z}_l$ ,因为两个wire可以属于不同的有限域,所以注意是不同的offset $\Delta$ 。
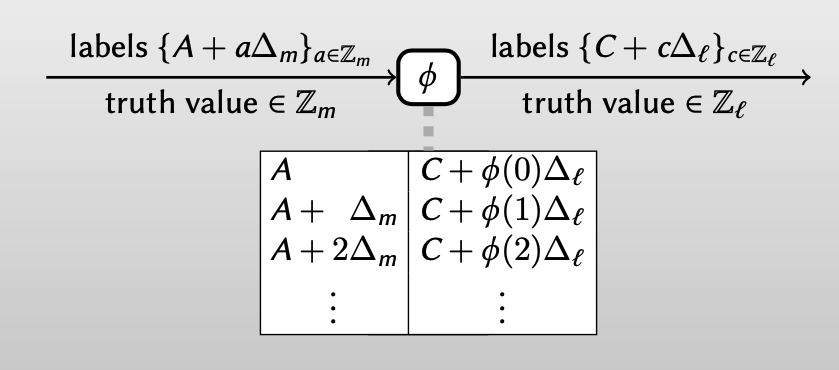
因此,使用generalized free XOR技术garble unary gates需要$m$个ciphertexts。

当然如果加上row reduction技术,只需要 $m-1$ 个ciphertexts。
因为作用在 $\mathbb{Z}_m$ 上,所以为了减少evaluator的开销,一般化point-and-permute技术, color bits $\in \mathbb{Z}_m$ 。
Generalized garbling tool
通过generalized free xor的思想,我们可以高效混淆有如下特征的电路:
- Each wire has a preferred modulus $\mathbb{Z}_m$
- Wire-label-offset $\Delta_m$ global to all $\mathbb{Z}_m$ -wires
- Addition gates: all wires touching gate have same modulus
- Garbling cost: free
- Mult-by-constant gates: input/output wires have same modulus
- Garbling cost: free
- Unary gates: $\mathbb{Z}_m$ input and $\mathbb{Z}_l$ output
- Garbling cost: $m-1$ ciphertexts
Arithmetic computations
为什么要引入arithmetic circuits,因为他往往会比传统布尔电路高效,以一个32-bit的数为例,使用half-gates技术来混淆一些常见运算,结果如下:

而如果使用上文提到的generalized garbling tool,加法操作和乘以常数操作的开销都降为0,而模 $m$ 乘法操作的开销为 $2m-2$ ciphetextes(讲座中没有详细讲解,方法是generalization of half-gates),同样以32-bit的数为例,和传统布尔电路技术对比:
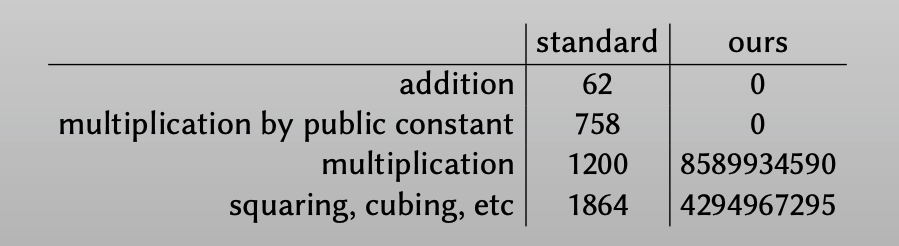
可见对于32-bit的乘法、开方操作,使用generalized garbling技术开销非常大,因为这是和 $m$ 相关的。
CRT form
而这个可以通过中国剩余定理(Chinese remainder theorem, CRT)来进行优化。
相较于之前在 $\mathbb{Z}_{32}=\mathbb{Z}_{4294967296}$ 进行算数运算,通过CRT可以在 $\mathbb{Z}_{2\cdot 3\cdot 5\cdot 7\cdot 11\cdots 29}=\mathbb{Z}_{6469693239}$ 下进行高效的乘法、开方操作。
通过把一个32-bit的数 $x$ 表示为 $(x\%2, x\%3,x\%5,\cdots,x\%29)$ ,对每个余数单独进行算数运算,最后通过中国剩余定理,即可求解出结果。
将使用CRT表示方法的系统与上述方法比较:

可见,用CRT的表示方法能大幅降低garbled circuits的开销。但是CRT的表示方法同样也带来了一些问题:
- Not so good:
- Converting from binary to CRT is not so good.
- Getting CRT valurs into the citcuit via OT is not so good.
- Kinda bad: (room for improvement)
- Comparing two CRT-encoded values
- Converting from CRT to binaty
- Integer division
- Modular reduction different than the CRT composite modulus (e.g., garbled RSA)
下面会主要介绍如何比较两个CRT表示方法的数字。
Comparing CRT values
下表是CRT的表示方法,可以看出CRT的表示方法不能直接对数字进行比较:
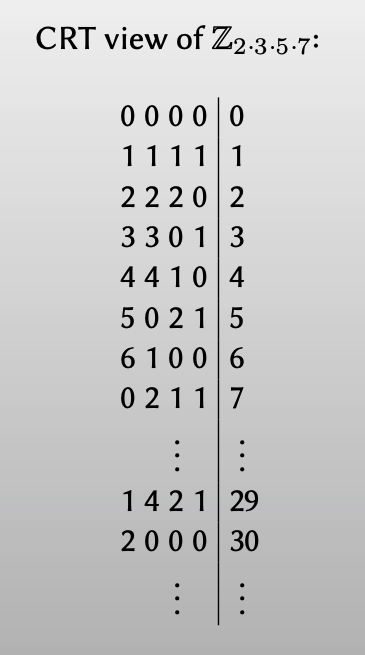
但如果将CRT转换为一种叫PMR (Primorial Mixed Radix)的表示方法,就可以直接对数字进行比较了:
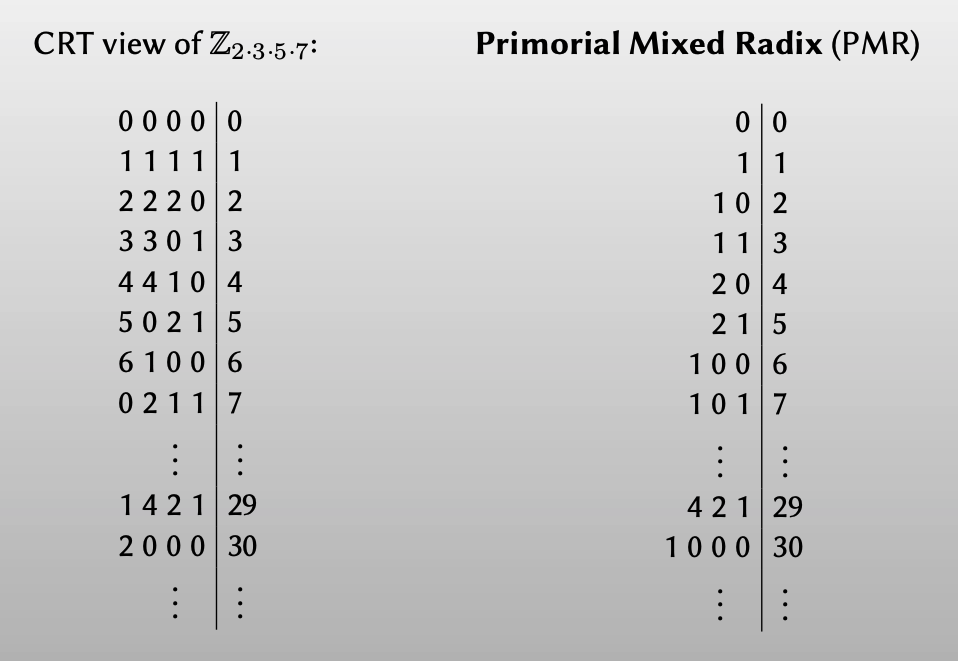
转换方法如下图所示:

要实现上述的转换方法,只需要实现 $(x\%p, x\%q)\mapsto \lfloor \frac{x}{p}\rfloor\%q$ 模块的garbled circuits。
实现该模块的具体步骤可以参考下图:

Subtract x%3 − x%5 (mod 7 is fine)【相减】
- “Project” x%3 and x%5 to $\mathbb{Z}_7$ wires
- Subtract mod 7 for free
Result has the same “constant segments” as what we want
Apply unary projection:【再做一个一元映射】

最后分析一下CRT表示方式的比较效率:
- $(x\%p, x\%q)\mapsto \lfloor \frac{x}{p}\rfloor\%q$ 模块大约需要 $2p+2q$ 的开销。
而将CRT转换为PMR:对于每一个质数对都需要上述模块。
对于k-bit: CRT比较 $O(k^3)$

「MPC-Mike Rosulek 」:Advanced Techniques and Optimizations for Garbled Circuits

