「Cryptography-MIT6875」: Lecture 1

In this series, I will learn MIT 6.875, Foundations of Cryptography, lectured by Vinod Vaikuntanathan.
Any corrections and advice are welcome. ^ - ^

Everything you’ve ever wanted is on the other side of fear.

Topics:

• Introduction to cryptography
• Secure Communication and Shannon’s definitions of perfect secrecy
• Perfect Indistinguishability definitions.
• The One-time pad construction
• Shannon’s lower bound.

Introduction

6.875 is about Crypto, not Cryptocurrencies.

6.875 is about foundations, including Digital Signatures, Zero-knowledge Proofs, Public-key Encryption, Homomorphic Encryption, Threshold Cryptography, Pseudorandomness and so on.

The Intellectual Origins

Claude E. Shannon

• The paper, “Communication Theory of Secrecy Systems”(1945), gave a way to define some terms in Secure Communication.
• The paper, “A mathematical Theory of Communication”(1948), founded Information Theory.

Alan M. Turing

• He was engaged on Cryptanalysis of Enigma Machine in 1938-39.
• The paper, “On Computable Numbers, with an Application to the Entscheidungsproblem”(1936), give birth to Computer Science.

Modern Cryptography

Modern Cryptography is a Practice to Theory and Back.

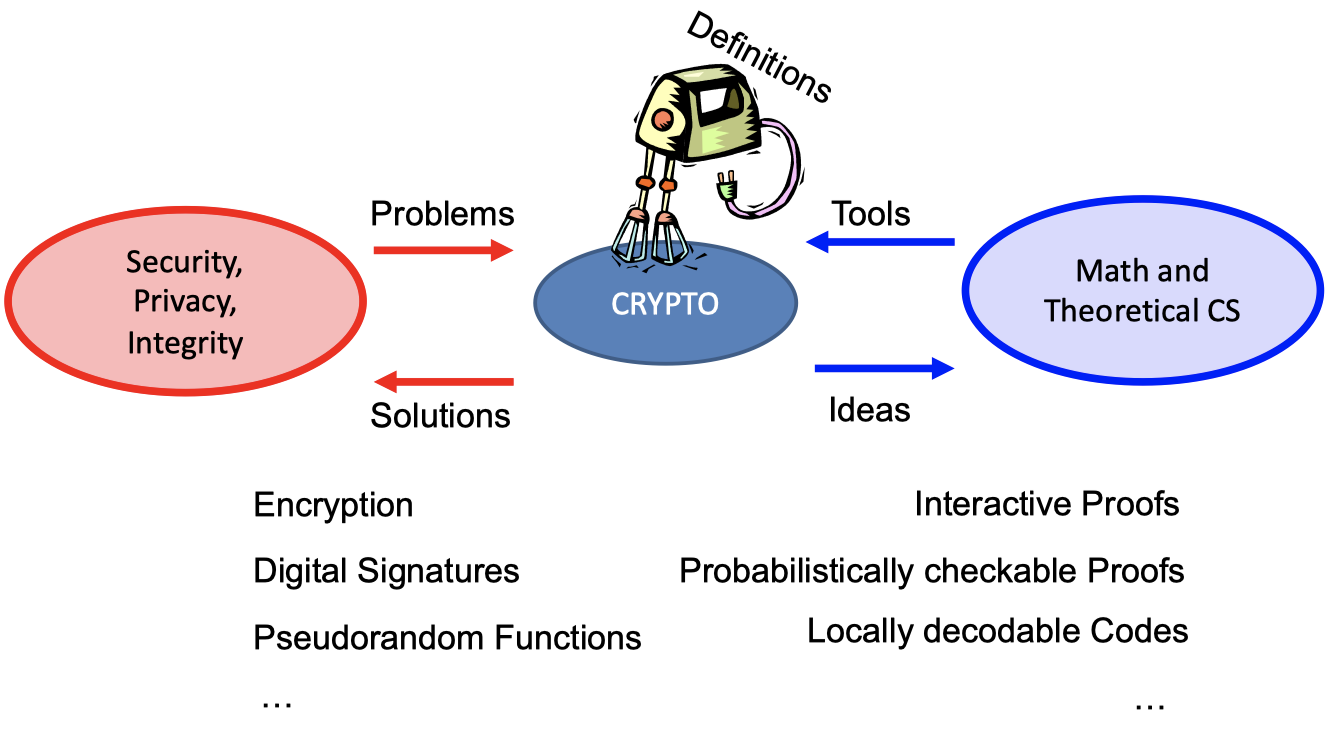
• The Definitions in CRYPTO are important.
• It solves the problems of Security, Privacy, Integrity(etc.) using Encryption, Digital Signatures, Pseudorandom Functions(etc.).
• It makes use of the ideas in Math and Theoretical CS to construct some tools, such as Interactive Proofs, Probabilistically checkable Proofs, Locally decodable Codes etc.

6.875 Themes

1. The Omnipresent, Worst-case, Adversary.

   1. The central idea is to model the adversary.
      What they know? What they can do? What their goals are?
   2. Definitions will be our friend.
      If you cannot define something, you cannot achieve it.
   3. A key takeaway from 6.875.
      Cryptographic(or, adversarial) thinking.
      【这门课最重要的是培养一种从攻击者角度的思考方式，如何才能抵抗哪些未知的攻击】

2. Computational Hardness will be our enabler.

   1. The central theme is to use cryptographic leash.
      Use computational hardness to “tame” the adversary.
      【计算难度将是有利的工具】

   2. Number theory is a classic source of hard problem.
      【数论是困难问题的经典来源】

      [G.H.Hardy, “A Mathematician’s Apology”]

      ”Both Gauss and lesser mathematicians may be justified in rejoicing that there is one such science [number theory] at any rate, whose very remoteness from ordinary human activities should keep it gentle and clean”
      【高斯和一些数学家都会认为应该保持数论的纯洁性，即使它远离一般的人类活动。】

      3. More recently, people get inspiration from geometry, coding theory, combinatorics.
         【现在，也会从几何学、编码理论、组合学中获得困难问题】

3. Security Proofs via Reductions.

   1. The proof usually comes in a from of reduction.
      【安全证明往往会规约为一种困难问题的求解】
      ” If there is an (efficient) adversary that breaks scheme A w.r.t definition D, then there is an (efficient) adversary that factors large number”
   2. The reductions in 6.875 will be probabilistic and significantly more involved than the NP-hardness reductions.
      【这门课所涉及的规约将是概率性的，比NP难度中的规约更复杂】

6.875 Topics

6.875 will cover these topics.

• Pseudorandomness
  【伪随机性】
• Secret-key Encryption and Authentication
  【对称加密和认证】
• Public-key Encryption and Digital Signatures
  【公钥加密和数字签名】
• Cryptographic Hashing
  【哈希】
• Zero-knowledge Proofs
  【零知识证明】
• Secure Multiparty Computation
  【安全多方计算】
• Private Information Retrieval
  【隐私信息检索】
• Homomorphic Encryption
  【同态加密】
• Advanced topics： Threshold Cryptography, Differential Privacy, …
  【前沿课题：门限密码，差分隐私等】

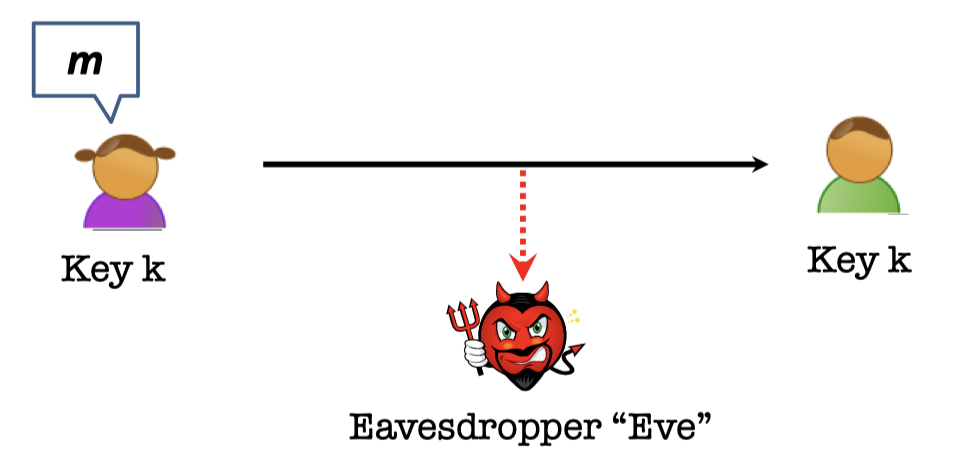
Secure Communication

The scenario in Secure Communication is that Alice wants to send a message M to Bob without revealing it to Eve.

It’s actually very difficult.

However, it can be achievable in such a setting which Alice and Bob meet beforehand to agree on a secret key k.

Symmetric-key Encryption

In order to achieve Symmetric-key Encryption, it is necessary to design three (possibly probabilistic) polynomial-time algorithm.

• Key Generation Algorithm Gen: $k\leftarrow \mathrm{Gen}(1^n)$
  It has to be probabilistic (or, random).
  n is the desired output length.w
• Encryption Algorithm Enc: $c\leftarrow \mathrm{Enc}(k,m)$
• Decryption Algorithm Dec: $m\leftarrow \mathrm{Dec}(k,c)$

The Worst-case Adversary

What dose the worst-case adversary looks like?

• It’s actually an arbitrary computationally unbounded algorithm EVE.
  【实际上是一个计算能力无限的任意算法】
• It knows Alice and Bob’s algorithms Gen, Enc and Dec but does not know the key nor their internal randomness.
  【算法公开，只有密钥是未知的】

Kerckhoff’s principle or Shannon’s maxim:
- Gen, Enc and Dec are public algorithms.
- The key is private.

• It can see the ciphertexts going through the channel.
  【能够看到信道里的密文】
  (but cannot modify them…)

Consequently, Security Definition actually defines what the adversary is trying to learn?

What dose the security definition looks like? (intuitive)
EVE should learning nothing about m from ciphertext c.

$$ \forall \mathrm{EVE}, \mathrm{Pr}[\mathrm{EVE(Dec}(k,c)=m)]\le \frac{1}{\mathcal{M}} $$

where k is generated by $k\leftarrow \mathrm{Gen}(1^n)$ and m is sampled in $m\leftarrow \mathcal{M}$ supposing $\mathcal{M}$ is probabilistic uniform distribution.

It’s important to note that $\mathcal{M}$ is an arbitrary distribution as a matter of fact. The only thing we can control is the distribution of k.
【M的分布实际上是任意的，但我们能控制k的分布】

Two Equiv. Def.s of Security

In this section, I will introduce two equivalent definitions of security, Shannon’s perfect Secrecy Definition and Perfect Indistinguishable Definition.

It will be easier to prove one of them in some cases.

Shannon’s Perfect Secrecy Def.

The main idea in Shannon’s perfect secrecy definition is the posteriori of attacker is equal to the priori of the attacker, i.e. A-posteriori= A-priori.

【香农安全定义的主要思想是，攻击者的后验概率等于先验概率，也就是说攻击者看到密文后获得的信息（后验）和看到密文前得到的信息（先验）是一样的】

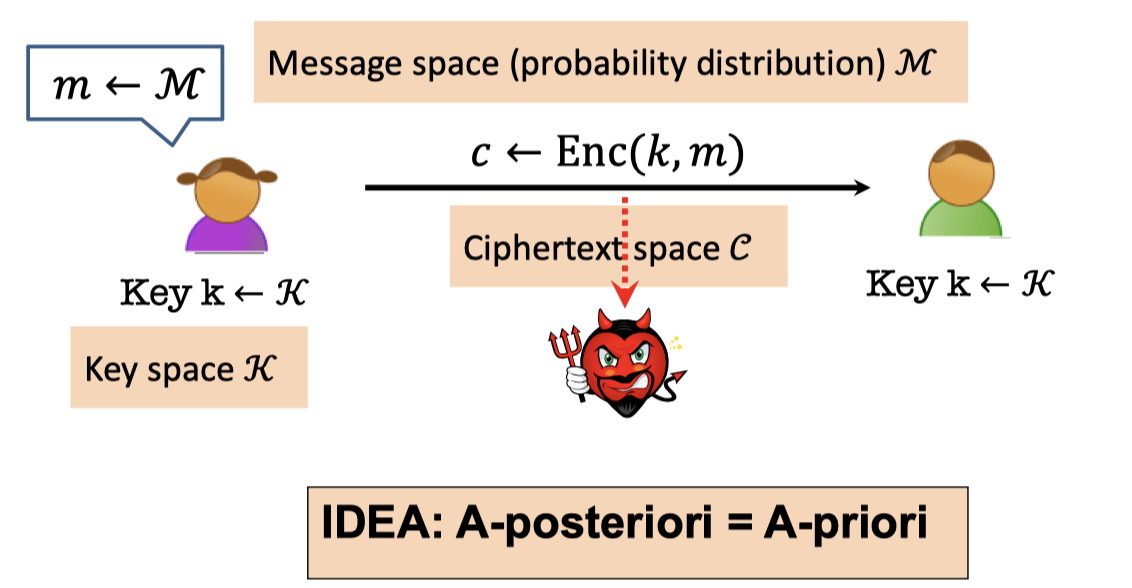
** Shannon’s Perfect Secrecy Definition: **

$$ \begin{array}{l}\forall\mathcal{M}, \forall m\in \operatorname{Supp}(\mathcal{M}),\forall c\in \operatorname{Supp}(\mathcal{C}) , \\ \qquad \qquad \qquad \operatorname{Pr}\left[\mathcal{M}=m \mid \operatorname{Enc}(\mathcal{K}, \mathcal{M})=c\right]=\operatorname{Pr}[\mathcal{M}=m]\end{array} $$

where $\mathcal{M,K,C}$ are variables in message space, key space and ciphertext space respectively.

There are two worlds, real world and ideal world.

• A-posteriori represents the real world.
  In real world, the attacker can see the ciphertext in the channel.
  So the probability that the attacker knows the message is m when the ciphertext c is known is $\operatorname{Pr}\left[\mathcal{M}=m \mid \operatorname{Enc}(\mathcal{K}, \mathcal{M})=c\right]$ .
• A-priori represents the ideal world.
  In ideal world, the attacker can only guess the message when the ciphertext is unknown. So the probability is $\operatorname{Pr}[\mathcal{M}=m]$ .

Perfect Indistinguishability Def.

Perfect indistinguishability is a formalizaton of a turing test.

There are two worlds, world 0 and world 1.

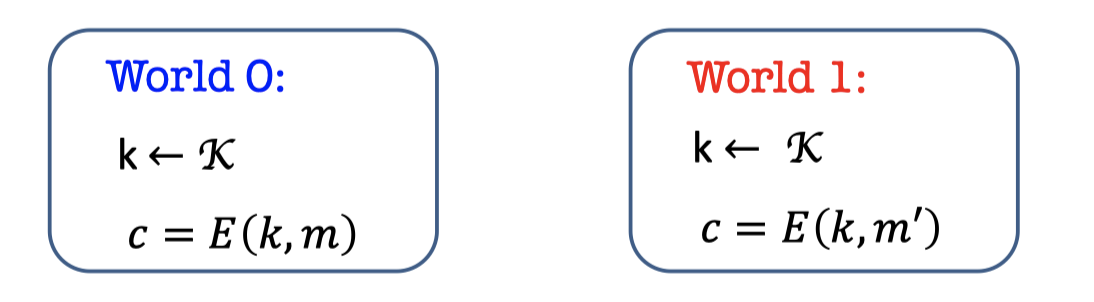
• The two worlds both sample the key $k$ from the key space $\mathcal{K}$, and the world 0 uses $k$ to encrypt $m$ while world 1 uses $k$ to encrypt $m’$.
• The attacker is a distinguisher that gets the $c$ and tries to guess which world she’s in.

【有两个世界，一个世界用随机密钥加密$m$，另一个用随机密钥加密$m’$，攻击者希望能根据密文区分她在哪一个世界】

** Perfect Indistinguishability Definition: **

$$ \begin{array}{l}\forall\mathcal{M}, \forall m,m'\in \operatorname{Supp}(\mathcal{M}),\forall c\in \operatorname{Supp}(\mathcal{C}) , \\ \qquad \qquad \qquad \operatorname{Pr}\left[\operatorname{Enc}(\mathcal{K}, m)=c\right]=\operatorname{Pr}\left[\operatorname{Enc}(\mathcal{K}, m')=c\right]\end{array} $$

where $\mathcal{M,K,C}$ are variables in message space, key space and ciphertext space respectively.

The Two Def.s are Equiv.

The two definitions are equivalent.

** Theorem: **

An encryption scheme (Gen, Enc, Dec) satisfies secrecy IFF it satisfies perfect indistinguishability.

The proof is simple use of Bayes’ Theorem.

Indistinguishability → Secrecy

Here we prove that if it satisfies perfect indistinguishability then it satisfies perfect secrecy.

We know indistinguishability(IND)

$$ \begin{array}{l}\forall\mathcal{M}, \forall m,m'\in \operatorname{Supp}(\mathcal{M}),\forall c\in \operatorname{Supp}(\mathcal{C}) , \\ \qquad \qquad \qquad \operatorname{Pr}\left[\operatorname{Enc}(\mathcal{K}, m)=c\right]=\operatorname{Pr}\left[\operatorname{Enc}(\mathcal{K}, m')=c\right]\end{array} $$

We want secrecy(SEC)

$$ \begin{array}{l}\forall\mathcal{M}, \forall m\in \operatorname{Supp}(\mathcal{M}),\forall c\in \operatorname{Supp}(\mathcal{C}) , \\ \qquad \qquad \qquad \operatorname{Pr}\left[\mathcal{M}=m \mid \operatorname{Enc}(\mathcal{K}, \mathcal{M})=c\right]=\operatorname{Pr}[\mathcal{M}=m]\end{array} $$

** Proof: **

1. Suppose tha the Probability is equal to $\alpha$ in IND.

2. There is a key observation.
   $\forall m \operatorname{Pr}[\operatorname{Enc}(\mathcal{K,M})=c]=\operatorname{Pr}[\operatorname{Enc}(\mathcal{K},m)=c]$

   The key and the message are both random in left while the message is fixed in right.
   Proof:

   1. $\operatorname{Pr}[\operatorname{Enc}(\mathcal{K,M})=c]$
   2. = $\sum\operatorname{Pr}[\operatorname{Enc}(\mathcal{K,M})=c\mid \mathcal{M}=m]; \operatorname{Pr}[\mathcal{M}=m]$
   3. = $\sum\operatorname{Pr}[\operatorname{Enc}(\mathcal{K},m)=c]; \operatorname{Pr}[\mathcal{M}=m]$
   4. = $\alpha \sum\operatorname{Pr}[\mathcal{M}=m]$
   5. = $\alpha$

3. We can use Bayes’ theorem and the key observation to deduce the SEC.

   1. $\operatorname{Pr}\left[\mathcal{M}=m \mid \operatorname{Enc}(\mathcal{K}, \mathcal{M})=c\right]$
   2. = $\frac{\operatorname{Pr}\left[\operatorname{Enc}(\mathcal{K}, \mathcal{M})=c\mid \mathcal{M}=m \right] \operatorname{Pr}[\mathcal{M}=m]}{\operatorname{Pr}\left[ \operatorname{Enc}(\mathcal{K}, \mathcal{M})=c\right]}$ (Bayes)
   3. = $\frac{\operatorname{Pr}\left[\operatorname{Enc}(\mathcal{K}, m)=c \right] \operatorname{Pr}[\mathcal{M}=m]}{\operatorname{Pr}\left[ \operatorname{Enc}(\mathcal{K}, \mathcal{M})=c\right]}$
   4. = $\frac{\alpha \operatorname{Pr}[\mathcal{M}=m]}{\alpha}$ （key observation)
   5. = $\operatorname{Pr}[\mathcal{M}=m]$

Secrecy → Indistinguishability

Here we prove that if it satisfies perfect secrecy then it satisfies perfect indistinguishability.

We know secrecy(SEC)

$$
\begin{array}{l}\forall\mathcal{M}, \forall m\in \operatorname{Supp}(\mathcal{M}),\forall c\in \operatorname{Supp}(\mathcal{C}) , \ \qquad \qquad \qquad \operatorname{Pr}\left[\mathcal{M}=m \mid \operatorname{Enc}(\mathcal{K}, \mathcal{M})=c\right]=\operatorname{Pr}[\mathcal{M}=m]\end{array}
$$

We want indistinguishability(IND)

$$
\begin{array}{l}\forall\mathcal{M}, \forall m,m’\in \operatorname{Supp}(\mathcal{M}),\forall c\in \operatorname{Supp}(\mathcal{C}) , \ \qquad \qquad \qquad \operatorname{Pr}\left[\operatorname{Enc}(\mathcal{K}, m)=c\right]=\operatorname{Pr}\left[\operatorname{Enc}(\mathcal{K}, m’)=c\right]\end{array}
$$

** Proof: **

1. Just prove the above key observation.
   1. $\operatorname{Pr}\left[\operatorname{Enc}(\mathcal{K}, m)=c\right]$
   2. = $\operatorname{Pr}\left[\operatorname{Enc}(\mathcal{K}, \mathcal{M})=c\mid \mathcal{M}=m \right]$
   3. = $\frac{\operatorname{Pr}\left[ \mathcal{M}=m\mid\operatorname{Enc}(\mathcal{K}, \mathcal{M})=c \right]\operatorname{Pr}[\operatorname{Enc}(\mathcal{K}, \mathcal{M})=c ]}{\operatorname{Pr}[\mathcal{M}=m]}$ (Bayes)
   4. From SEC, we know:$\operatorname{Pr}\left[\mathcal{M}=m \mid \operatorname{Enc}(\mathcal{K}, \mathcal{M})=c\right]=\operatorname{Pr}[\mathcal{M}=m]$
   5. = $\operatorname{Pr}[\operatorname{Enc}(\mathcal{K}, \mathcal{M})=c ]$
   6. = $\operatorname{Pr}[\operatorname{Enc}(\mathcal{K}, m’)=c ]$

One-time Pad

Perfect Secrecy is achievable using one-time pad.

Perfect Secrecy is Achievable

The One-time Pad Construction:

• Gen: choose an n-bit string k at random, i.e. $k\leftarrow {0,1}^n$
• Enc(k,m), where M is an n-bit message: Output $c=m\oplus k$
• Dec(k, c): Output $m=c\oplus k$

xor property:

1. uniformity
   X is a uniform variable and $Y$ is a random variable.
   Then $Z=X\oplus Y$ is a uniform variable.
2. randomness
   $X$ is a fixed value and $Y$ is a random variable.
   The $Z=X\oplus Y$ is a random variable.

Correctness can be easily verified. $c\oplus k=(m\oplus k)\oplus k=m$.

** Claim: **

One-time Pad achieves Perfect Indistinguishability (and therefore perfect secrecy)

** Proof: **

It requires that for any $m,m’$, $c\in{0,1}^n$,
$\operatorname{Pr}[\operatorname{Enc}(\mathcal{K},m)=c]=\operatorname{Pr}[\operatorname{Enc}(\mathcal{K},m’)=c]$

1. $\operatorname{Pr}[\operatorname{Enc}(\mathcal{K},m)=c]$
   1. = $\operatorname{Pr}[\mathcal{K}\oplus m=c]$
   2. = $\operatorname{Pr}[\mathcal{K}= m\oplus c]$
   3. = $1/2^n$
2. $\operatorname{Pr}[\operatorname{Enc}(\mathcal{K},m’)=c]$
   1. = $\operatorname{Pr}[\mathcal{K}\oplus m’=c]$
   2. = $\operatorname{Pr}[\mathcal{K}= m’\oplus c]$
   3. = $1/2^n$
3. QED.

Reusing a One-time Pad?

Is it secure when we reuse a one-time Pad?

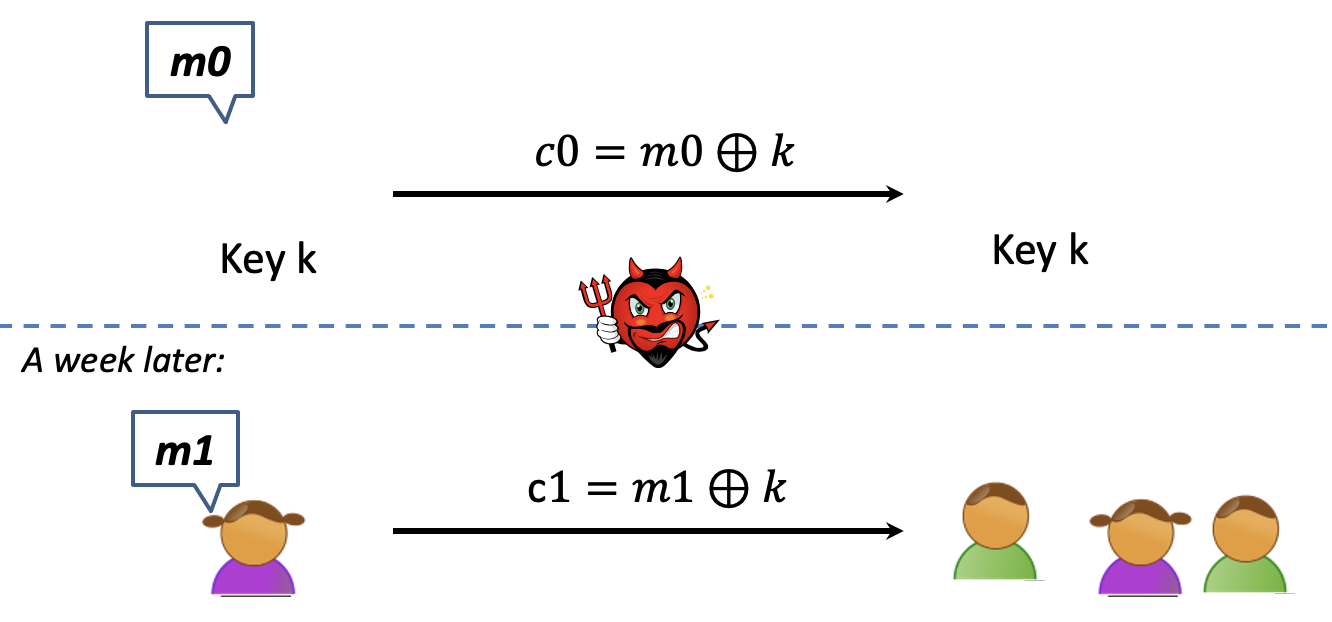
The answer is absolutely no.

** Claim: **

One-time Pad does not achieve Perfect Indistinguishability (and therefore not perfect secrecy).

** Proof: **

It requires that for all pairs $(m_0,m_1),(m_0’,m_1’),(c_0,c_1)\in{0,1}^{2n}$,$\operatorname{Pr}[\operatorname{Enc}(k, m _0)=c_0 \text { and } \operatorname{Enc}(k, m_1)=c_1]=\operatorname{Pr}[\operatorname{Enc}(k, m _0’)=c_0 \text { and } \operatorname{Enc}(k, m_1’)=c_1]$

1. We want to pick $(m_0,m_1),(m_0’,m_1’),(c_0,c_1)\in{0,1}^{2n}$ which makes the left of the equation not equal to the right.
2. Pick $m_0=m_1=m,m_0’\ne m_1’$ and $c_0=c_1=c$
   1. The left side
      1. $\operatorname{Pr}[\operatorname{Enc}(k, m _0)=c_0 \text { and } \operatorname{Enc}(k, m_1)=c_1]$
      2. = $\operatorname{Pr}[\operatorname{Enc}(k, m )=c]$
      3. = $1/2^n$
   2. The right side
      1. $\operatorname{Pr}[\operatorname{Enc}(k, m _0’)=c_0 \text { and } \operatorname{Enc}(k, m_1’)=c_1]$
      2. = 0
3. QED.

A Serious Limitation

Perfect secrecy has its price.

A serious limitation of perfect secrecy is that the key space must be greater than or equal to the message space.

** Theorem: **

For any perfectly secure encryption scheme, $\mathcal{|K|\ge|M|}$.

** Proof(by picture): **

Assume for contradiction that $\mathcal{|K|<|M|}$.

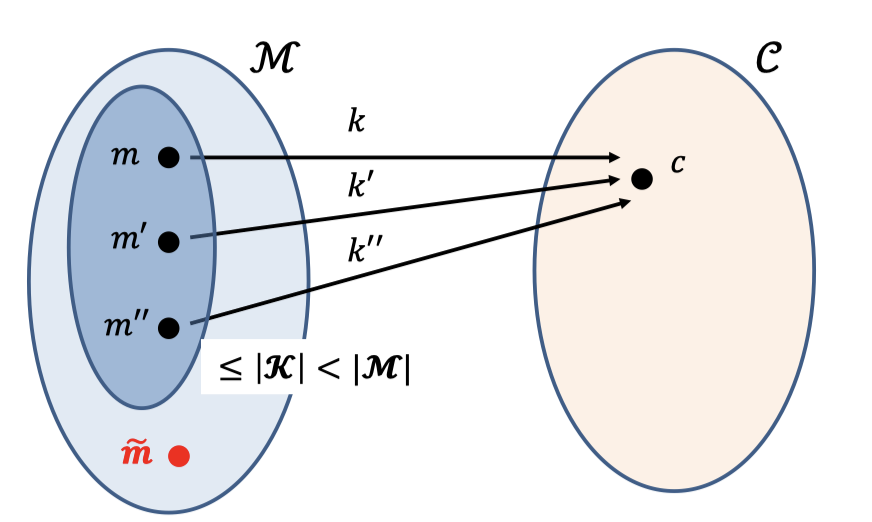
• If we pick any $c\in \mathcal{C}$, there are at most $|\mathcal{K}|$ possible messages using distinct keys.
  Suppose the possible message space is the bluer part in the left ellipse which the size is at most $|\mathcal{K}|$ and less than $\mathcal{|M|}$ .
• Choose the message $m$ inside the bluer part. $m$ is the possible message.So the probability is $\operatorname{Pr}[\operatorname{Enc}(\mathcal{K},m)=c]>0$.
• Choose the message $\tilde{m}$ outside the bluer part. $\tilde{m}$ can’t be the possible message. So the probability is $\operatorname{Pr}[\operatorname{Enc}(\mathcal{K},\tilde{m})=c]=0$
• There is a contradiction.

Solution

So, what are we to do?

The solution is to RELAX the definition.

The adversary we mentioned above is an arbitrary computationally unbounded algorithm EVE.

Now, we relax the adversary to an arbitrary computationally bounded algorithm.