「机器学习-李宏毅」：HW2-Binary Income Predicting

   机器学习-李宏毅 34 minutes read (About 5066 words) 0 visits

这篇文章中，手刻实现了「机器学习-李宏毅」的HW2-Binary Income Prediction的作业。分别用Logistic Regression和Generative Model实现。
包括对数据集的处理，训练模型，可视化，预测等。
有关HW2的相关数据、源代码、预测结果等，欢迎光临小透明的GitHub

Task introduction and Dataset

Kaggle competition: link

Task: Binary Classification

Predict whether the income of an individual exceeds $50000 or not ?

*Dataset: * Census-Income (KDD) Dataset

(Remove unnecessary attributes and balance the ratio between positively and negatively labeled data)

Feature Format

  • train.csv, test_no_label.csv【都是没有处理过的数据，可作为数据参考和优化参考】

    • text-based raw data

    • unnecessary attributes removed, positive/negative ratio balanced.

  • X_train, Y_train, X_test【已经处理过的数据，可以直接使用】

    • discrete features in train.csv => one-hot encoding in X_train (education, martial state…)

    • continuous features in train.csv => remain the same in X_train (age, capital losses…).

    • X_train, X_test : each row contains one 510-dim feature represents a sample.

    • Y_train: label = 0 means “<= 50K” 、 label = 1 means “ >50K ”

注：数据集超大，用notepad查看比较舒服；调试时，也可以先调试小一点的数据集。

Logistic Regression

Logistic Regression 原理部分见这篇博客。

Prepare data

本文直接使用X_train Y_train X_test 已经处理好的数据集。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# prepare data
X_train_fpath = './data/X_train'
Y_train_fpath = './data/Y_Train'
X_test_fpath = './data/X_test'
output_fpath = './logistic_output/output_logistic.csv'
fpath = './logistic_output/logistic'

X_train = np.genfromtxt(X_train_fpath, delimiter=',')
Y_train = np.genfromtxt(Y_train_fpath, delimiter=',')
X_test = np.genfromtxt(X_test_fpath, delimiter=',')

X_train = X_train[1:, 1:]
Y_train = Y_train[1:, 1:]
X_test = X_test[1:, 1:]


统计一下数据集：

1
2
3
4
5
6
7
8
9
10
11
12
train_size = X_train.shape[0]
dev_size = X_dev.shape[0]
test_size = X_test.shape[0]
data_dim = X_train.shape[1]

with open(fpath, 'w') as f:
    f.write('In logistic model:\n')
    f.write('Size of Training set: {}\n'.format(train_size))
    f.write('Size of development set: {}\n'.format(dev_size))
    f.write('Size of test set: {}\n'.format(test_size))
    f.write('Dimension of data: {}\n'.format(data_dim))

结果如下：

1
2
3
4
5
In logistic model:
Size of Training set: 48830
Size of development set: 5426
Size of test set: 27622
Dimension of data: 510

normalize

normalize data.

对于train data，计算出每个feature的mean和std，保存下来用来normalize test data。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def _normalization(X, train=True, X_mean=None, X_std=None):
    # This function normalize columns of X.
    # Output:
    #       X: normalized data
    #       X_mean, X_std
    if train:
        X_mean = np.mean(X, axis=0)
        X_std = np.std(X, axis=0)
    for j in range(X.shape[1]):
        X[:, j] = (X[:, j] - X_mean[j]) / (X_std[j] + 1e-8)  # avoid X_std==0
    return X, X_mean, X_std
    
# Normalize train_data and test_data
X_train, X_mean, X_std = _normalization(X_train, train=True)
X_test, _, _ = _normalization(X_test, train=False, X_mean=X_mean, X_std=X_std)

Development set split

在logistic regression中使用的gradient，没有closed-form解，所以在train set中划出一部分作为development set 优化参数。

1
2
3
4
5
6
7
8
def _train_dev_split(X, Y, dev_ratio=0.25):
    # This function splits data into training set and development set.
    train_size = int(X.shape[0] * (1 - dev_ratio))
    return X[:train_size], Y[:train_size], X[train_size:], Y[train_size:]

# Split data into train data and development data
dev_ratio = 0.1
X_train, Y_train, X_dev, Y_dev = _train_dev_split(X_train, Y_train, dev_ratio=dev_ratio)

Useful function

_shuffle(X, Y)

本文使用mini-batch gradient。

所以在每次epoch时，以相同顺序同时打乱X_train,Y_train数组，再mini-batch。

1
2
3
4
5
6
7
8
np.random.seed(0)

def _shuffle(X, Y):
    # This function shuffles two two list/array, X and Y, together.
    randomize = np.arange(len(X))
    np.random.shuffle(randomize)
    return X[randomize], Y[randomize]

_sigmod(z)

计算 $\frac{1}{1+e^{-z}}$ ，注意：防止溢出，给函数返回值规定上界和下界。

1
2
3
4
5
def _sigmod(z):
    # Sigmod function can be used to compute probability
    # To avoid overflow
    return np.clip(1/(1.0 + np.exp(-z)), 1e-8, 1-(1e-8))

_f(X, w, b)

是sigmod函数的输入，linear part。

  • 输入：
    • X：shape = [size, data_dimension]
    • w：weight vector, shape = [data_dimension, 1]
    • b: bias, scalar
  • 输出：
    • 属于Class 1的概率（Label=0，即收入小于$50k的概率）
1
2
3
4
5
6
7
8
9
10
def _f(X, w, b):
    # This function is the linear part of sigmod function
    # Arguments:
    #   X: input data, shape = [size, data_dimension]
    #   w: weight vector, shape = [data_dimension, 1]
    #   b: bias, scalar
    # Output:
    #   predict probabilities
    return _sigmod(np.dot(X, w) + b)

_predict(X, w, b)

预测Label=0？（0或者1，不是概率）

1
2
3
4
def _predict(X, w, b):
    # This function returns a truth value prediction for each row of X belonging to class1(label=0)
    return np.around(_f(X, w, b)).astype(np.int)

_accuracy(Y_pred, Y_label)

计算预测出的结果（0或者1）和真实结果的正确率。

这里使用 $1-\overline{error}$ 来表示正确率。

1
2
3
4
5
6
def _accuracy(Y_pred, Y_label):
    # This function calculates prediction accuracy
    # Y_pred: 0 or 1
    acc = 1 - np.mean(np.abs(Y_pred - Y_label))
    return acc

_cross_entropy_loss(y_pred, Y_label)

计算预测出的概率（是sigmod的函数输出）和真实结果的交叉熵。

计算公式为： $\sum_n {C(y_{pred},Y_{label})}=-\sum[Y_{label}\ln{y_{pred}}+(1-Y_{label})\ln(1-{y_{pred}})]$ 

1
2
3
4
5
6
7
8
9
def _cross_entropy_loss(y_pred, Y_label):
    # This function calculates the cross entropy of Y_pred and Y_label
    #
    # Argument:
    #          y_pred: predictions, float vector
    #          Y_label: truth labels, bool vector
    cross_entropy = - np.dot(Y_label.T, np.log(y_pred)) - np.dot((1 - Y_label).T, np.log(1 - y_pred))
    return cross_entropy[0][0]

_gradient(X, Y_label, w, b)

和Regression的最小二乘一样。（严谨的说，最多一个系数不同）

1
2
3
4
5
6
7
8
def _gradient(X, Y_label, w, b):
    # This function calculates the gradient of cross entropy
    # X, Y_label, shape = [batch_size, ]
    y_pred = _f(X, w, b)
    pred_error = Y_label - y_pred
    w_grad = - np.dot(X.T, pred_error)
    b_grad = - np.sum(pred_error)
    return w_grad, float(b_grad)

Training (Adagrad)

初始化一些参数。

这里特别注意 :

由于adagrad的参数更新是 $w \longleftarrow w-\eta \frac{gradient}{ \sqrt{gradsum}}$ .

防止除0，初始化gradsum的值为一个较小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
# training by logistic model

# Initial weights and bias
w = np.zeros((data_dim, 1))
b = np.float(0.)
w_grad_sum = np.full((data_dim, 1), 1e-8)  # avoid divided by zeros
b_grad_sum = np.float(1e-8)

# Some parameters for training
epoch = 20
batch_size = 2**3
learning_rate = 0.2

Adagrad

Aagrad具体原理见这篇博客的1.2节。

迭代更新时，每次epoch计算一次loss和accuracy，以便可视化更新过程，调整参数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# Keep the loss and accuracy history at every epoch for plotting
train_loss = []
dev_loss = []
train_acc = []
dev_acc = []

# Iterative training
for it in range(epoch):
    # Random shuffle at every epoch
    X_train, Y_train = _shuffle(X_train, Y_train)

    # Mini-batch training
    for id in range(int(np.floor(train_size / batch_size))):
        X = X_train[id*batch_size: (id+1)*batch_size]
        Y = Y_train[id*batch_size: (id+1)*batch_size]

        # calculate gradient
        w_grad, b_grad = _gradient(X, Y, w, b)

        # adagrad gradient update
        w_grad_sum = w_grad_sum + w_grad**2
        b_grad_sum = b_grad_sum + b_grad**2
        w_ada = np.sqrt(w_grad_sum)
        b_ada = np.sqrt(b_grad_sum)
        w = w - learning_rate * w_grad / np.sqrt(w_grad_sum)
        b = b - learning_rate * b_grad / np.sqrt(b_grad_sum)

    # compute loss and accuracy of training set and development set at every epoch
    y_train_pred = _f(X_train, w, b)
    Y_train_pred = np.around(y_train_pred)
    train_loss.append(_cross_entropy_loss(y_train_pred, Y_train)/train_size)
    train_acc.append(_accuracy(Y_train_pred, Y_train))

    y_dev_pred = _f(X_dev, w, b)
    Y_dev_pred = np.around(y_dev_pred)
    dev_loss.append(_cross_entropy_loss(y_dev_pred, Y_dev)/dev_size)
    dev_acc.append(_accuracy(y_dev_pred, Y_dev))

Loss & accuracy

输出最后一次迭代的loss和accuracy。

结果如下：

1
2
3
4
Training loss: 0.2933570286596322
Training accuracy: 0.8839238173254147
Development loss: 0.31029505347634456
Development accuracy: 0.8336166253549906

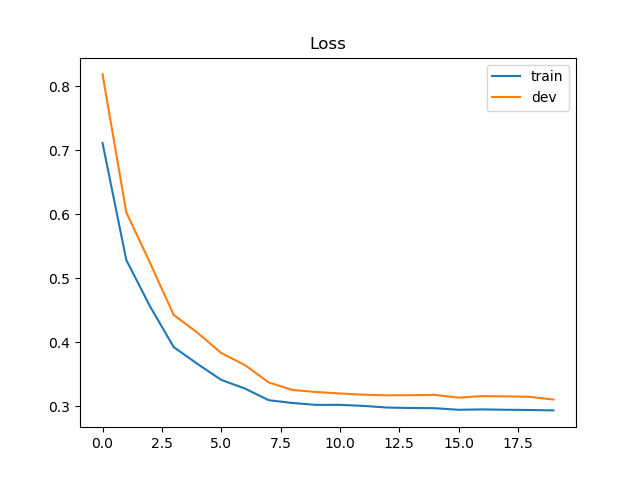
画出loss 和 accuracy的更新过程：

loss：

JPCjx0.png

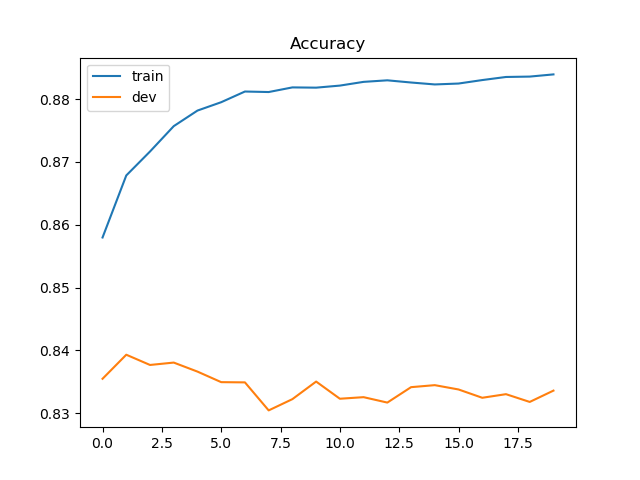
accuracy：

JPCxMV.png

由于Feature数量较大，将权重影响最大的feature输出看看：

1
2
3
4
5
6
7
8
9
10
Other Rel <18 spouse of subfamily RP: [7.11323764]
 Grandchild <18 ever marr not in subfamily: [6.8321061]
 Child <18 ever marr RP of subfamily: [6.77322397]
 Other Rel <18 ever marr RP of subfamily: [6.76688406]
 Other Rel <18 never married RP of subfamily: [6.37488958]
 Child <18 spouse of subfamily RP: [5.97717831]
 United-States: [5.53932651]
 Grandchild 18+ spouse of subfamily RP: [5.42948497]
 United-States: [5.41543809]
 Mexico: [4.79920763]

Code

完整数据集、代码等，欢迎光临小透明GitHub 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
#################
# Data:2020-04-05
# Author: Fred Lau
# ML-Lee: HW2 : Binary Classification
###########################################################
import numpy as np
import csv
import sys
import matplotlib.pyplot as plt

##########################################################
# prepare data
X_train_fpath = './data/X_train'
Y_train_fpath = './data/Y_Train'
X_test_fpath = './data/X_test'
output_fpath = './logistic_output/output_logistic.csv'
fpath = './logistic_output/logistic'

X_train = np.genfromtxt(X_train_fpath, delimiter=',')
Y_train = np.genfromtxt(Y_train_fpath, delimiter=',')
X_test = np.genfromtxt(X_test_fpath, delimiter=',')

X_train = X_train[1:, 1:]
Y_train = Y_train[1:, 1:]
X_test = X_test[1:, 1:]


def _normalization(X, train=True, X_mean=None, X_std=None):
    # This function normalize columns of X.
    # Output:
    #       X: normalized data
    #       X_mean, X_std
    if train:
        X_mean = np.mean(X, axis=0)
        X_std = np.std(X, axis=0)
    for j in range(X.shape[1]):
        X[:, j] = (X[:, j] - X_mean[j]) / (X_std[j] + 1e-8)  # avoid X_std==0
    return X, X_mean, X_std


def _train_dev_split(X, Y, dev_ratio=0.25):
    # This function splits data into training set and development set.
    train_size = int(X.shape[0] * (1 - dev_ratio))
    return X[:train_size], Y[:train_size], X[train_size:], Y[train_size:]


# Normalize train_data and test_data
X_train, X_mean, X_std = _normalization(X_train, train=True)
X_test, _, _ = _normalization(X_test, train=False, X_mean=X_mean, X_std=X_std)

# Split data into train data and development data
dev_ratio = 0.1
X_train, Y_train, X_dev, Y_dev = _train_dev_split(X_train, Y_train, dev_ratio=dev_ratio)

train_size = X_train.shape[0]
dev_size = X_dev.shape[0]
test_size = X_test.shape[0]
data_dim = X_train.shape[1]

with open(fpath, 'w') as f:
    f.write('In logistic model:\n')
    f.write('Size of Training set: {}\n'.format(train_size))
    f.write('Size of development set: {}\n'.format(dev_size))
    f.write('Size of test set: {}\n'.format(test_size))
    f.write('Dimension of data: {}\n'.format(data_dim))


np.random.seed(0)

###############################################################
# useful function

def _shuffle(X, Y):
    # This function shuffles two two list/array, X and Y, together.
    randomize = np.arange(len(X))
    np.random.shuffle(randomize)
    return X[randomize], Y[randomize]

def _sigmod(z):
    # Sigmod function can be used to calculate probability
    # To avoid overflow
    return np.clip(1 / (1.0 + np.exp(-z)), 1e-8, 1 - (1e-8))


def _f(X, w, b):
    # This is the logistic function, parameterized by w and b
    #
    # Arguments:
    #   X: input data, shape = [batch_size, data_dimension]
    #   w: weight vector, shape = [data_dimension, 1]
    #   b: bias, scalar
    # Output:
    #       predict probability of each row of X being positively labeled, shape = [batch_size, 1]
    return _sigmod(np.dot(X, w) + b)


def _predict(X, w, b):
    # This fucntion returns a truth value prediction for each row of X by logistic regression
    return np.around(_f(X, w, b)).astype(np.int)


def _accuracy(Y_pred, Y_label):
    # This function calculates prediction accuracy
    # Y_pred: 0 or 1
    acc = 1 - np.mean(np.abs(Y_pred - Y_label))
    return acc


def _cross_entropy_loss(y_pred, Y_label):
    # This function calculates the cross entropy of Y_pred and Y_label
    #
    # Argument:
    #          y_pred: predictions, float vector
    #          Y_label: truth labels, bool vector
    cross_entropy = - np.dot(Y_label.T, np.log(y_pred)) - np.dot((1 - Y_label).T, np.log(1 - y_pred))
    return cross_entropy[0][0]


def _gradient(X, Y_label, w, b):
    # This function calculates the gradient of cross entropy
    # X, Y_label, shape = [batch_size, ]
    y_pred = _f(X, w, b)
    pred_error = Y_label - y_pred
    w_grad = - np.dot(X.T, pred_error)
    b_grad = - np.sum(pred_error)
    return w_grad, float(b_grad)


#######################################
# training by logistic model

# Initial weights and bias
w = np.zeros((data_dim, 1))
b = np.float(0.)
w_grad_sum = np.full((data_dim, 1), 1e-8)  # avoid divided by zeros
b_grad_sum = np.float(1e-8)

# Some parameters for training
epoch = 20
batch_size = 2**3
learning_rate = 0.2

# Keep the loss and accuracy history at every epoch for plotting
train_loss = []
dev_loss = []
train_acc = []
dev_acc = []

# Iterative training
for it in range(epoch):
    # Random shuffle at every epoch
    X_train, Y_train = _shuffle(X_train, Y_train)

    # Mini-batch training
    for id in range(int(np.floor(train_size / batch_size))):
        X = X_train[id*batch_size: (id+1)*batch_size]
        Y = Y_train[id*batch_size: (id+1)*batch_size]

        # calculate gradient
        w_grad, b_grad = _gradient(X, Y, w, b)

        # adagrad gradient update
        w_grad_sum = w_grad_sum + w_grad**2
        b_grad_sum = b_grad_sum + b_grad**2
        w_ada = np.sqrt(w_grad_sum)
        b_ada = np.sqrt(b_grad_sum)
        w = w - learning_rate * w_grad / np.sqrt(w_grad_sum)
        b = b - learning_rate * b_grad / np.sqrt(b_grad_sum)

    # compute loss and accuracy of training set and development set at every epoch
    y_train_pred = _f(X_train, w, b)
    Y_train_pred = np.around(y_train_pred)
    train_loss.append(_cross_entropy_loss(y_train_pred, Y_train)/train_size)
    train_acc.append(_accuracy(Y_train_pred, Y_train))

    y_dev_pred = _f(X_dev, w, b)
    Y_dev_pred = np.around(y_dev_pred)
    dev_loss.append(_cross_entropy_loss(y_dev_pred, Y_dev)/dev_size)
    dev_acc.append(_accuracy(y_dev_pred, Y_dev))

with open(fpath, 'a') as f:
    f.write('Training loss: {}\n'.format(train_loss[-1]))
    f.write('Training accuracy: {}\n'.format(train_acc[-1]))
    f.write('Development loss: {}\n'.format(dev_loss[-1]))
    f.write('Development accuracy: {}\n'.format(dev_acc[-1]))

###################
# Plotting Loss and accuracy curve
# Loss curve
plt.plot(train_loss, label='train')
plt.plot(dev_loss, label='dev')
plt.title('Loss')
plt.legend()
plt.savefig('./logistic_output/loss.png')
plt.show()

plt.plot(train_acc, label='train')
plt.plot(dev_acc, label='dev')
plt.title('Accuracy')
plt.legend()
plt.savefig('./logistic_output/acc.png')
plt.show()

#################################
# Predict
predictions = _predict(X_test, w, b)
with open(output_fpath, 'w') as f:
    f.write('id, label\n')
    for id, label in enumerate(predictions):
        f.write('{}, {}\n'.format(id, label[0]))

###############################
# Output the weights and bias
ind = (np.argsort(np.abs(w), axis=0)[::-1]).reshape(1, -1)

with open(X_test_fpath) as f:
    content = f.readline().strip('\n').split(',')
content = content[1:]

with open(fpath, 'a') as f:
    for i in ind[0, 0: 10]:
       f.write('{}: {}\n'.format(content[i], w[i]))

Generative Model

Generative Model 原理部分见 这篇博客

Prepare data

这部分和Logistic regression一样。

只是，因为generative model有closed-form solution，不需要划分development set。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# Prepare data
X_train_fpath = './data/X_train'
Y_train_fpath = './data/Y_train'
X_test_fpath = './data/X_test'
output_fpath = './generative_output/output_{}.csv'
fpath = './generative_output/generative'

X_train = np.genfromtxt(X_train_fpath, delimiter=',')
Y_train = np.genfromtxt(Y_train_fpath, delimiter=',')
X_test = np.genfromtxt(X_test_fpath, delimiter=',')

X_train = X_train[1:, 1:]
Y_train = Y_train[1:, 1:]
X_test = X_test[1:, 1:]

def _normalization(X, train=True, X_mean=None, X_std=None):
    # This function normalize columns of X
    # Output:
    #       X: normalized data
    #       X_mean, X_std
    if train:
        X_mean = np.mean(X, axis=0)
        X_std = np.std(X, axis=0)
    for j in range(X.shape[1]):
       X[:, j] = (X[:, j] - X_mean[j]) / (X_std[j] + 1e-8)  # avoid X_std==0
    return X, X_mean, X_std

# Normalize train_data and test_data
X_train, X_mean, X_std = _normalization(X_train, train=True)
X_test, _, _ = _normalization(X_test, train=False, X_mean=X_mean, X_std=X_std)

train_size = X_train.shape[0]
test_size = X_test.shape[0]
data_dim = X_train.shape[1]

with open(fpath, 'w') as f:
    f.write('In generative model:\n')
    f.write('Size of training data: {}\n'.format(train_size))
    f.write('Size of test set: {}\n'.format(test_size))
    f.write('Dimension of data: {}\n\n'.format(data_dim))

Useful functions

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Useful functions
def _sigmod(z):
    # Sigmod function can be used to compute probability
    # To avoid overflow
    return np.clip(1/(1.0 + np.exp(-z)), 1e-8, 1-(1e-8))

def _f(X, w, b):
    # This function is the linear part of sigmod function
    # Arguments:
    #   X: input data, shape = [size, data_dimension]
    #   w: weight vector, shape = [data_dimension, 1]
    #   b: bias, scalar
    # Output:
    #   predict probabilities
    return _sigmod(np.dot(X, w) + b)

def _predict(X, w, b):
    # This function returns a truth value prediction for each row of X belonging to class1(label=0)
    return np.around(_f(X, w, b)).astype(np.int)

def _accuracy(Y_pred, Y_label):
    # This function computes prediction accuracy
    # Y_pred: 0 or 1
    acc = 1 - np.mean(np.abs(Y_pred - Y_label))
    return acc

Training

公式再推导

计算公式：

$$ \begin{equation}\begin{aligned}P\left(C_{1} | x\right)&=\frac{P\left(x | C_{1}\right) P\left(C_{1}\right)}{P\left(x | C_{1}\right) P\left(C_{1}\right)+P\left(x | C_{2}\right) P\left(C_{2}\right)}\\&=\frac{1}{1+\frac{P\left(x | C_{2}\right) P\left(C_{2}\right)}{P\left(x | C_{1}\right) P\left(C_{1}\right)}}\\&=\frac{1}{1+\exp (-z)} =\sigma(z)\qquad(z=\ln \frac{P\left(x | C_{1}\right) P\left(C_{1}\right)}{P\left(x | C_{2}\right) P\left(C_{2}\right)}\end{aligned}\end{equation} $$

计算z的过程：

  1. 首先计算Prior Probability。
  2. 假设模型是Gaussian的，算出 $\mu_1,\mu_2 ,\Sigma$ 的closed-form solution 。
  3. 根据 $\mu_1,\mu_2,\Sigma$ 计算出 $w,b$ 。

  1. 计算Prior Probability。

    程序中用list comprehension处理较简单。

    1
    2
    3
    4
    # compute in-class mean
    X_train_0 = np.array([x for x, y in zip(X_train, Y_train) if y == 0])
    X_train_1 = np.array([x for x, y in zip(X_train, Y_train) if y == 1])

  2. 计算 $\mu_1,\mu_2 ,\Sigma$ （Gaussian）

    $\mu_0=\frac{1}{C0} \sum_{n=1}^{C0} x^{n} $ (Label=0)

    $\mu_1=\frac{1}{C1} \sum_{n=1}^{C1} x^{n} $ (Label=0)

    $\Sigma_0=\frac{1}{C0} \sum_{n=1}^{C0}\left(x^{n}-\mu^{}\right)^{T}\left(x^{n}-\mu^{}\right)$ (注意 ：这里的 $x^n,\mu$ 都是行向量，注意转置的位置）

    $\Sigma_1=\frac{1}{C1} \sum_{n=1}^{C1}\left(x^{n}-\mu^{}\right)^{T}\left(x^{n}-\mu^{}\right)$

    $\Sigma=(C0 \times\Sigma_0+C1\times\Sigma_1)/(C0+C1)$ (shared covariance) 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    mean_0 = np.mean(X_train_0, axis=0)
    mean_1 = np.mean(X_train_1, axis=0)

    # compute in-class covariance
    cov_0 = np.zeros(shape=(data_dim, data_dim))
    cov_1 = np.zeros(shape=(data_dim, data_dim))

    for x in X_train_0:
        # (D,1)@(1,D) np.matmul(np.transpose([x]), x)
        cov_0 += np.matmul(np.transpose([x - mean_0]), [x - mean_0]) / X_train_0.shape[0]
    for x in X_train_1:
        cov_1 += np.dot(np.transpose([x - mean_1]), [x - mean_1]) / X_train_1.shape[0]

    # shared covariance
    cov = (cov_0 * X_train_0.shape[0] + cov_1 * X_train_1.shape[0]) / (X_train.shape[0])

  1. 计算 $w,b$

    在 这篇博客中的第2小节中的公式推导中， $x^n,\mu$ 都是列向量，公式如下：

    $$ z=\left(\mu^{1}-\mu^{2}\right)^{T} \Sigma^{-1} x-\frac{1}{2}\left(\mu^{1}\right)^{T} \Sigma^{-1} \mu^{1}+\frac{1}{2}\left(\mu^{2}\right)^{T} \Sigma^{-1} \mu^{2}+\ln \frac{N_{1}}{N_{2}} $$ $w^T=\left(\mu^{1}-\mu^{2}\right)^{T} \Sigma^{-1} \qquad b=-\frac{1}{2}\left(\mu^{1}\right)^{T} \Sigma^{-1} \mu^{1}+\frac{1}{2}\left(\mu^{2}\right)^{T} \Sigma^{-1} \mu^{2}+\ln \frac{N_{1}}{N_{2}}$

    但是 ，一般我们在处理的数据集，$x^n,\mu$ 都是行向量。推导过程相同，公式如下：

    （主要注意转置和矩阵乘积顺序）

    $$ z=x\cdot \Sigma^{-1}\left(\mu^{1}-\mu^{2}\right)^{T} -\frac{1}{2} \mu^{1}\Sigma^{-1}\left(\mu^{1}\right)^{T}+\frac{1}{2}\mu^{2}\Sigma^{-1} \left(\mu^{2}\right)^{T} +\ln \frac{N_{1}}{N_{2}} $$ $w=\Sigma^{-1}\left(\mu^{1}-\mu^{2}\right)^{T} \qquad b=-\frac{1}{2} \mu^{1}\Sigma^{-1}\left(\mu^{1}\right)^{T}+\frac{1}{2}\mu^{2}\Sigma^{-1} \left(\mu^{2}\right)^{T} +\ln \frac{N_{1}}{N_{2}}$

但是，协方差矩阵的逆怎么求呢？

numpy中有直接求逆矩阵的方法(np.linalg.inv)，但当该矩阵是nearly singular，是奇异矩阵时，就会报错。

而我们的协方差矩阵（510*510）很大，很难保证他不是奇异矩阵。

于是，有一个 牛逼 强大的数学方法，叫SVD(singular value decomposition, 奇异值分解) 。

原理步骤我……还没有完全搞清楚QAQ（先挖个坑）[1]

利用SVD，可以将任何一个矩阵（即使是奇异矩阵），分界成 $A=u s v^T$ 的形式：其中u,v都是标准正交矩阵，s是对角矩阵。（numpy.linalg.svd方法实现了SVD）

可以利用SVD求矩阵的伪逆

  • $A=u s v^T$
    • u,v是标准正交矩阵，其逆矩阵等于其转置矩阵
    • s是对角矩阵，其”逆矩阵“（注意s矩阵的对角也可能有0元素） 将非0元素取倒数即可。
  • $A^{-1}=v s^{-1} u$

计算 $w,b$ 的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# compute weights and bias
# Since covariance matrix may be nearly singular, np.linalg.in() may give a large numerical error.
# Via SVD decomposition, one can get matrix inverse efficiently and  accurately.
# cov = u@s@vh
# cov_inv = dot(vh.T * 1 / s, u.T)
u, s, vh = np.linalg.svd(cov, full_matrices=False)
s_inv = s  # s_inv avoid <1e-8
for i in range(s.shape[0]):
    if s[i] < (1e-8):
        break
    s_inv[i] = 1./s[i]
cov_inv = np.matmul(vh.T * s_inv, u.T)

w = np.matmul(cov_inv, np.transpose([mean_0 - mean_1]))
b = (-0.5) * np.dot(mean_0, np.matmul(cov_inv, mean_0.T)) + (0.5) * np.dot(mean_1, np.matmul(cov_inv, mean_1.T)) + np.log(float(X_train_0.shape[0]) / X_train_1.shape[0])

Accuracy

accuracy结果：

1
Training accuracy: 0.8756450899439694

也将权重较大的feature输出看看：

1
2
3
4
5
6
7
8
9
10
age: [-0.51867291]
 Masters degree(MA MS MEng MEd MSW MBA): [-0.49912643]
 Spouse of householder: [0.49786805]
weeks worked in year: [-0.44710924]
 Spouse of householder: [-0.43305697]
capital gains: [-0.42608727]
dividends from stocks: [-0.41994666]
 Doctorate degree(PhD EdD): [-0.39310961]
num persons worked for employer: [-0.37345994]
 Prof school degree (MD DDS DVM LLB JD): [-0.35594107]

Code

具体数据集和代码，欢迎光临小透明GitHub 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134

import numpy as np

np.random.seed(0)
##############################################
# Prepare data
X_train_fpath = './data/X_train'
Y_train_fpath = './data/Y_train'
X_test_fpath = './data/X_test'
output_fpath = './generative_output/output_{}.csv'
fpath = './generative_output/generative'

X_train = np.genfromtxt(X_train_fpath, delimiter=',')
Y_train = np.genfromtxt(Y_train_fpath, delimiter=',')
X_test = np.genfromtxt(X_test_fpath, delimiter=',')

X_train = X_train[1:, 1:]
Y_train = Y_train[1:, 1:]
X_test = X_test[1:, 1:]

def _normalization(X, train=True, X_mean=None, X_std=None):
    # This function normalize columns of X
    # Output:
    #       X: normalized data
    #       X_mean, X_std
    if train:
        X_mean = np.mean(X, axis=0)
        X_std = np.std(X, axis=0)
    for j in range(X.shape[1]):
       X[:, j] = (X[:, j] - X_mean[j]) / (X_std[j] + 1e-8)  # avoid X_std==0
    return X, X_mean, X_std

# Normalize train_data and test_data
X_train, X_mean, X_std = _normalization(X_train, train=True)
X_test, _, _ = _normalization(X_test, train=False, X_mean=X_mean, X_std=X_std)

train_size = X_train.shape[0]
test_size = X_test.shape[0]
data_dim = X_train.shape[1]

with open(fpath, 'w') as f:
    f.write('In generative model:\n')
    f.write('Size of training data: {}\n'.format(train_size))
    f.write('Size of test set: {}\n'.format(test_size))
    f.write('Dimension of data: {}\n\n'.format(data_dim))

########################
# Useful functions
def _sigmod(z):
    # Sigmod function can be used to compute probability
    # To avoid overflow
    return np.clip(1/(1.0 + np.exp(-z)), 1e-8, 1-(1e-8))

def _f(X, w, b):
    # This function is the linear part of sigmod function
    # Arguments:
    #   X: input data, shape = [size, data_dimension]
    #   w: weight vector, shape = [data_dimension, 1]
    #   b: bias, scalar
    # Output:
    #   predict probabilities
    return _sigmod(np.dot(X, w) + b)

def _predict(X, w, b):
    # This function returns a truth value prediction for each row of X belonging to class1(label=0)
    return np.around(_f(X, w, b)).astype(np.int)

def _accuracy(Y_pred, Y_label):
    # This function computes prediction accuracy
    # Y_pred: 0 or 1
    acc = 1 - np.mean(np.abs(Y_pred - Y_label))
    return acc

#######################
# Generative Model: closed-form solution, can be computed directly

# compute in-class mean
X_train_0 = np.array([x for x, y in zip(X_train, Y_train) if y == 0])
X_train_1 = np.array([x for x, y in zip(X_train, Y_train) if y == 1])

mean_0 = np.mean(X_train_0, axis=0)
mean_1 = np.mean(X_train_1, axis=0)

# compute in-class covariance
cov_0 = np.zeros(shape=(data_dim, data_dim))
cov_1 = np.zeros(shape=(data_dim, data_dim))

for x in X_train_0:
    # (D,1)@(1,D) np.matmul(np.transpose([x]), x)
    cov_0 += np.matmul(np.transpose([x - mean_0]), [x - mean_0]) / X_train_0.shape[0]
for x in X_train_1:
    cov_1 += np.dot(np.transpose([x - mean_1]), [x - mean_1]) / X_train_1.shape[0]

# shared covariance
cov = (cov_0 * X_train_0.shape[0] + cov_1 * X_train_1.shape[0]) / (X_train.shape[0])

# compute weights and bias
# Since covariance matrix may be nearly singular, np.linalg.in() may give a large numerical error.
# Via SVD decomposition, one can get matrix inverse efficiently and  accurately.
# cov = u@s@vh
# cov_inv = dot(vh.T * 1 / s, u.T)
u, s, vh = np.linalg.svd(cov, full_matrices=False)
s_inv = s  # s_inv avoid <1e-8
for i in range(s.shape[0]):
    if s[i] < (1e-8):
        break
    s_inv[i] = 1./s[i]
cov_inv = np.matmul(vh.T * s_inv, u.T)

w = np.matmul(cov_inv, np.transpose([mean_0 - mean_1]))
b = (-0.5) * np.dot(mean_0, np.matmul(cov_inv, mean_0.T)) + (0.5) * np.dot(mean_1, np.matmul(cov_inv, mean_1.T)) + np.log(float(X_train_0.shape[0]) / X_train_1.shape[0])

# compute accuracy on training set
Y_train_pred = 1 - _predict(X_train, w, b)
with open(fpath, 'a') as f:
    f.write('\nTraining accuracy: {}\n'.format(_accuracy(Y_train_pred, Y_train)))

# Predict
predictions = 1 - _predict(X_test, w, b)
with open(output_fpath.format('generative'), 'w') as f:
    f.write('id, label\n')
    for i, label in enumerate(predictions):
        f.write('{}, {}\n'.format(i, label))

# Output the most significant weight
with open(X_test_fpath) as f:
    content = f.readline().strip('\n').split(',')
content = content[1:]

ind = np.argsort(np.abs(np.concatenate(w)))[::-1]
with open(fpath, 'a')as f:
    for i in ind[0:10]:
        f.write('{}: {}\n'.format(content[i], w[i]))

Reference

  1. SVD原理，待补充

「机器学习-李宏毅」：HW2-Binary Income Predicting

https://f7ed.com/2020/04/15/ml-lee-hw2/

Author

f7ed

Posted on

2020-04-15

Updated on

2020-07-03

Licensed under

CC BY-NC-SA 4.0

 

Like this article? Support the author with

Comments

Email me
×