「机器学习-李宏毅」:Unsupervised-PCA
这篇文章详细讲解了无监督学习(Unsupervised learning)的PCA(主成分分析法)。
文章开篇从聚类(Clustering)引出Distributed Represention,其中粗略阐述了聚类中K-means和HAC(层次聚类)的思想。
文章的后半部分具体阐述了PCA的数学细节,PCA的去相关性性质,PCA的另一种解释角度(component的角度),PCA的不足等。
Unsupervised Learning
无监督学习分为两种:
Dimension Reduction:化繁为简。
function 只有input,能将高维、复杂的输入,抽象为低维的输出。
如下图,能将3D的折叠图像,抽象为一个2D的表示(把他摊开)。
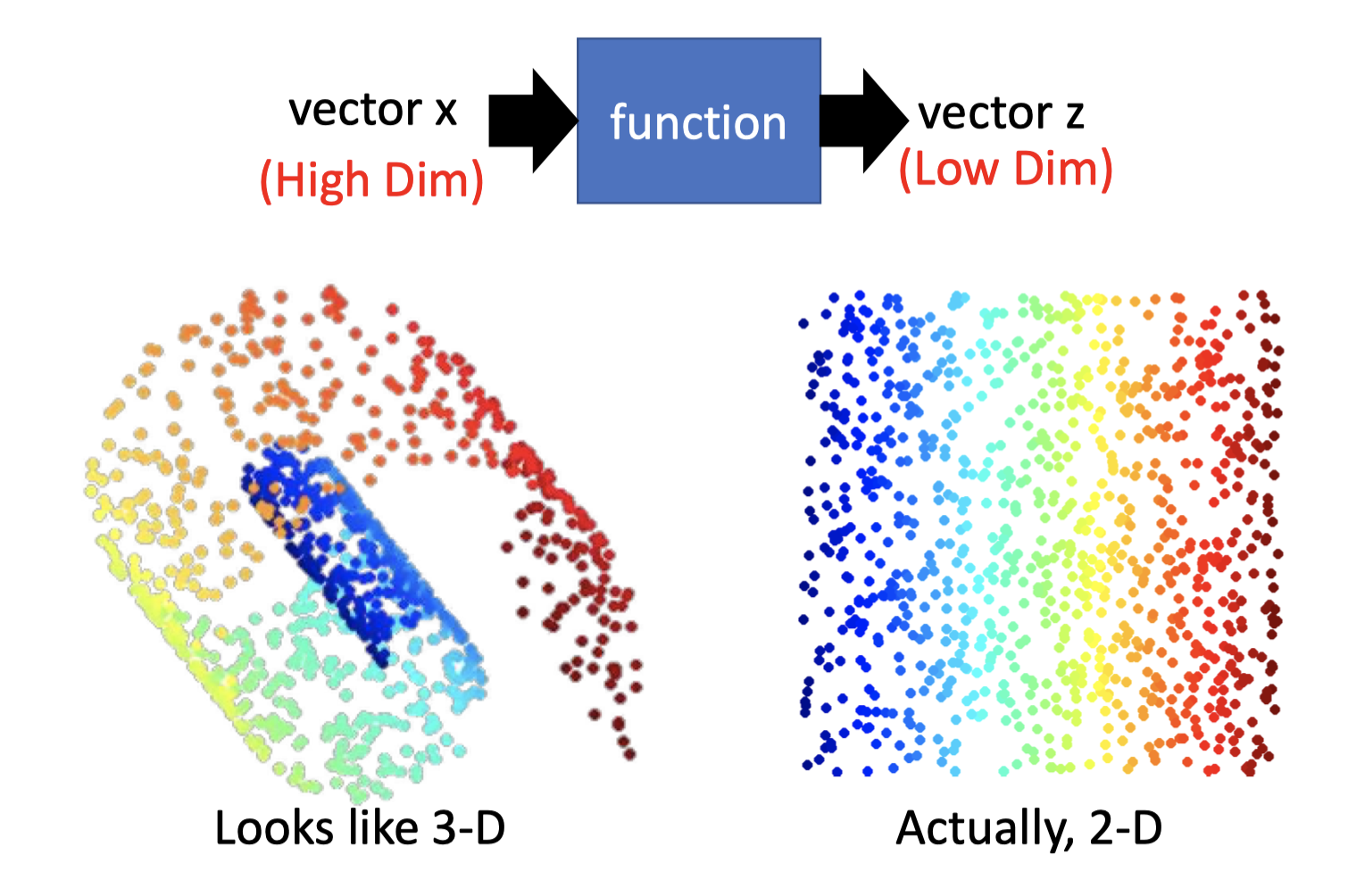
Generation:无中生有。
function 只有output。
(后面的博客会提及)
Dimension Reduction
此前,在semi-supervised learning的最后,提及过better presentation的思想,Dimension Reduction 其实就是这样的思想:去芜存菁,化繁为简。
比如,在MNIST中,一个数字的表示是28*28维度的向量(图如左),但大多28 *28维度的向量(图为右)都不是数字。

因此,在表达下图一众“3”的图像中,根本不需要28*28维的向量表示,1-D即可表示一张图(图片的旋转角度)。28 * 28的图像表示就像左边中老者的头发,1-D的表示就像老者的头,是对头发运动轨迹一种更简单的表达。
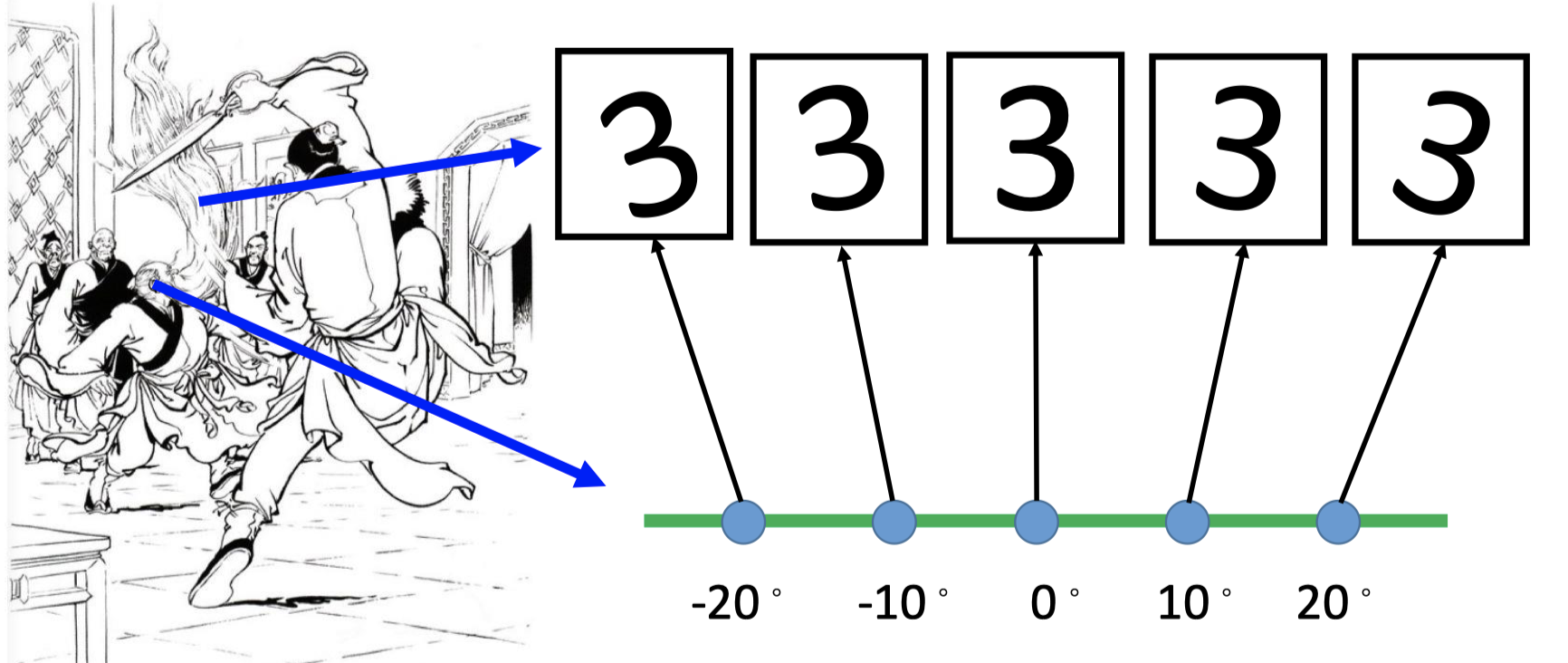
Clustering
在将Dimension Reduction之前,先将一种经典的无监督学习——clustering.
clustering也是一种降维的表达,将复杂的向量空间抽象为简单的类别,用某一个类别来表示该数据点。
这里主要讲述cluster的主要思想,算法细节可参考其他资料 。(待补充)
K-means
K-means的做法是:
Clustering $X=\left\{x^{1}, \cdots, x^{n}, \cdots, x^{N}\right\}$ into K clusters.
把所有data分为K个类,K的确定是empirical的,需要自己确定
Initialize cluster center $c^i, i=1,2,…,K$ .(K random $x^n$ from $X$)
初始化K个类的中心数据点,建议从training set $X$ 中随机选K 个点作为初始点。
不建议直接在向量空间中随机初始化K个中心点,因为很可能随机的中心点不属于任何一个cluster。
Repeat:根据中心点标记所属类,再更新新的中心点,重复直收敛。
For all $x^n$ in $X$ : 标记所属类。
$$ b_{i}^{n}\left\{\begin{array}{ll}1 & x^{n} \text { is most "close" to } c^{i} \\ 0 & \text { Otherwise }\end{array}\right. $$Updating all $c^i$ : $c^{i}=\sum_{x^{n}} b_{i}^{n} x^{n} / \sum_{x^{n}} b_{i}^{n}$ (计算该类中心点)
HAC:Hierarchical Agglomerative Clustering(HAC)
另一种clustering的方法是层次聚类(Hierarchical Clustering),这里介绍Agglomerative(自下而上)的策略。
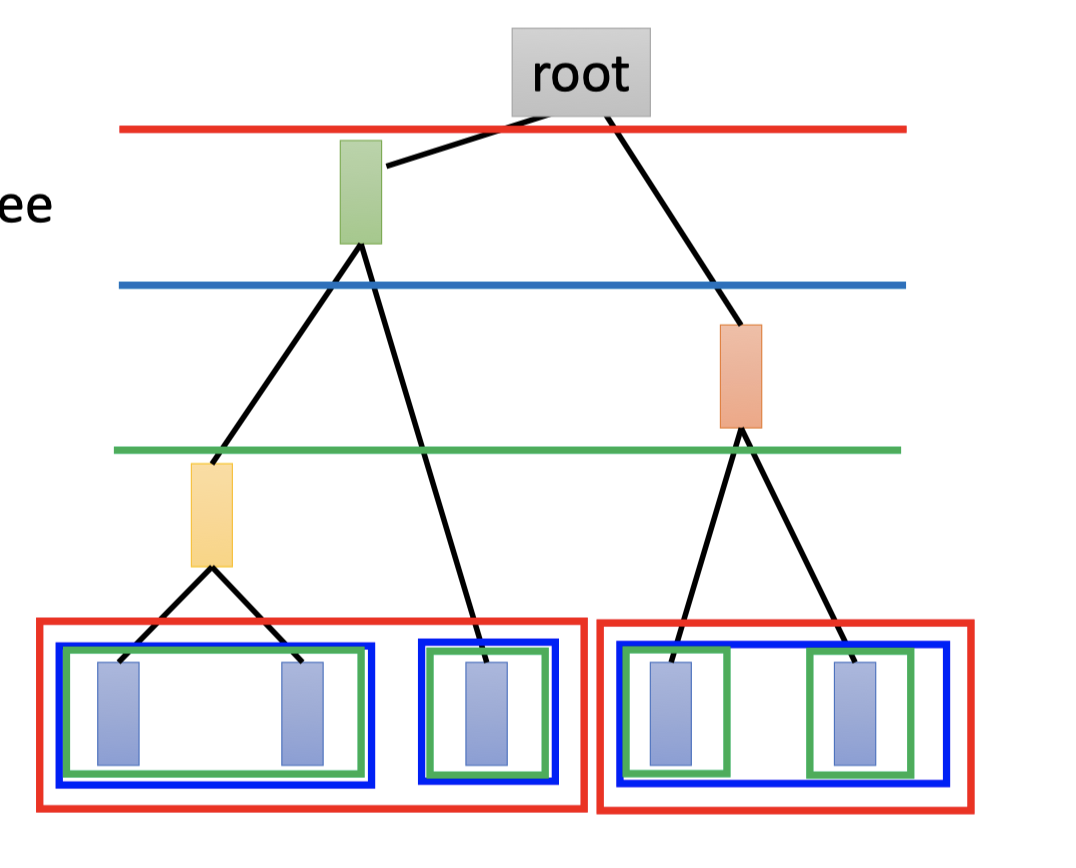
Build a tree.
- 如上图中,计算当前两两数据点(点或组合)的相似度(欧几里得距离或其他)。
- 选出最相近的两个合为一组(即连接在同一父子结点上,如最左边的两个)
- 重复1-2直至最后合为root。
该树中,越早分支的点集合,说明越不像。
Pick a threshold.
选一个阈值,即从哪个地方开始划开,比如选上图中红色的线作为阈值,那么点集分为两个cluseter,蓝色、绿色同理。
HAC和K-means相比,HAC不直接决定cluster的数目,而是通过决定threshold的值间接决定cluster的数目。
Distributed Representation
Cluster:an object must belong to one cluster.
在做聚类时,一个数据点必须标注为某一具体类别。这往往会丢失很多信息,比如一个人可能是70%的外向,30%的内敛,如果做clustering,就将这个人直接归为外向,这样的表示过于粗糙。
因此仍用vector来表示这个人,如下图。
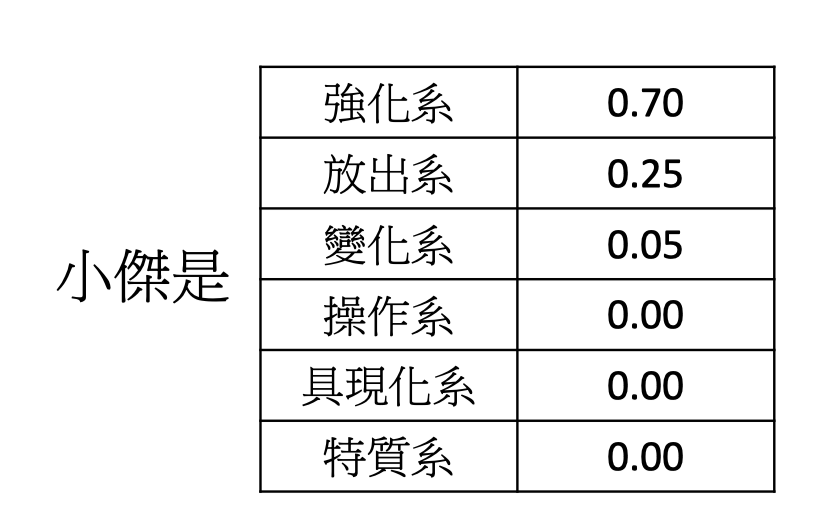
Distributed Representation(也叫Dimension Reduction)就是:一个高维的vector通过function,得到一个低维的vector。
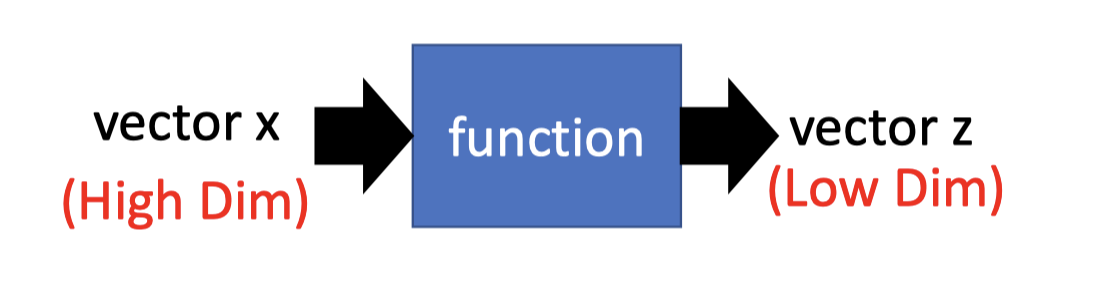
Distributed的方法有常见的两种:
Feature selection:
如下图数据点的分布,可以直接选择feature $x_2$ .
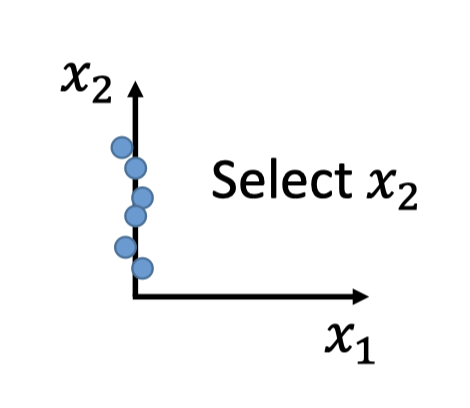
但这种方法往往只能处理2-D的情况,对于下图这种3-D情况往往不好做特征选择。
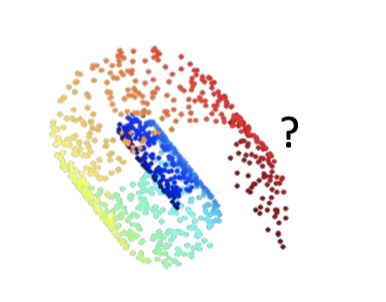
Principle component analysis(PCA)
另一种方法就是著名的PCA,主成分分析法。
PCA中,这个function就是一个简单的linear function($W$),通过 $z=Wx$ ,将高维的 $x$ 转化为低维的 $z$ .
PCA:Principle Component Analysis
PCA的参考资料见Bishop, Chapter12.
PCA就是要找 $z=Wx$ 中的 $W$ .
Main Idea
Reduce 1-D
如果将dimension reduce to 1-D,那么可以得出 $z_1 = w^1\cdot x$ .
$w^1$ 是vector,$x$ 是vector,做内积。
如下图,内积即投影,将所有的点 $x$ 投影到 $w^1$ 方向上,然后得到对应的 $z_1$ 值。
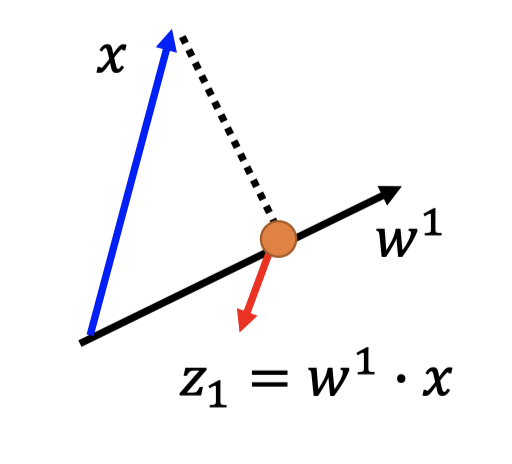
而对于得到的一系列 $z_1$ 值,我们希望 $z_1$ 的variance越大越好。
因为 $z_1$ 的分布越大,用 $z_1$ 来刻画数据,才能更好的区分数据点。
如下图,如果 $w^1$ 的方向是small variance的方向,那么这些点会集中在一起,而large variance方向,$z_1$ 能更好的刻画数据。
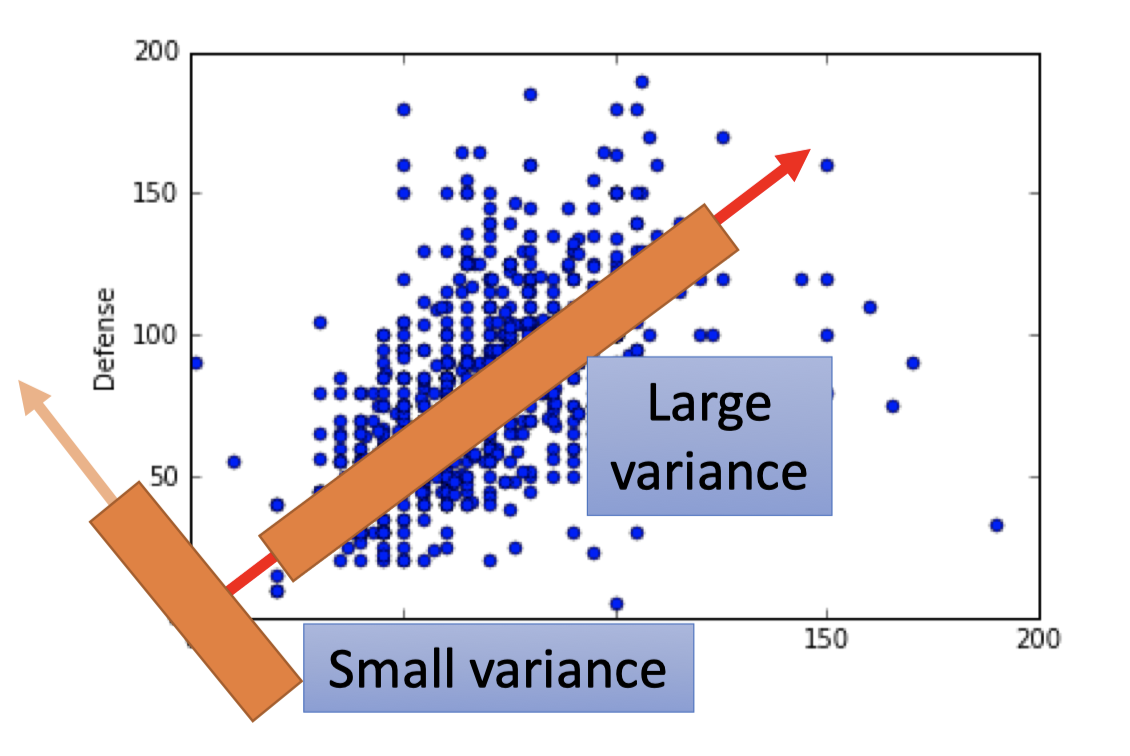
$z_1$ 的数学表达是: $ \operatorname{Var}\left(z_{1}\right)=\frac{1}{N} \sum_{z_{1}}\left(z_{1}-\overline{z_{1}}\right)^{2} \quad \left\|w^{1}\right\|_{2}=1$ (后文解释为什么要 $w^1$ 的长度为1)
Reduce 2-D
同理,如果将dimension reduce to 2-D .
$z=Wx$ 即
$$ \left\{ \begin{array}{11}z_1=w^1\cdot x \\ z_2=w^2 \cdot x \end{array} \right. ,\quad W=\begin{bmatrix}(w^1)^T \\ (w^2)^T \end{bmatrix} $$将所有点 $x$ 投影到 $w^1$ 方向,得到对应的 $z_1$ ,且让 $z_1$ 的分布尽可能的大:
$$ \operatorname{Var}\left(z_{1}\right)=\frac{1}{N} \sum_{z_{1}}\left(z_{1}-\overline{z_{1}}\right)^{2} ,\quad \left\|w^{1}\right\|_{2}=1 $$将所有点投影到 $w^2$ 方向,得到对应的 $z_2$ ,同样让 $z_2$ 的分布也尽可能大,再加一个约束条件,让 $w^2$ 和 $w^1$ 正交(后文会具体解释为什么)
$$ \operatorname{Var}\left(z_{2}\right)=\frac{1}{N} \sum_{z_{2}}\left(z_{2}-\overline{z_{2}}\right)^{2} ,\quad \left\|w^{2}\right\|_{2}=1 ,\quad w^1\cdot w^2=0 $$因此矩阵 $W$ 是Orthogonal matrix (正交矩阵)。
Detail[Warning of Math
想跳过math部分的,可以直接看Conclusion。
1-D中:
Goal:find $w^1$ to maximum $(w^1)^T S w^1$ s.t.$(w^1)^Tw^1=1$
结论:$w^1$ 就是协方差矩阵 $S$ 最大特征值 $\lambda_1 $ 对应的特征向量。 s.t.$(w^1)^Tw^1=1$
2-D中:
Goal:find $w^2$ to maximum $(w^2)^TSw^2 $ s.t. $(w^2)^Tw^2=1, (w^2)^Tw^1=0$
结论:$w^2$ 就是协方差矩阵$S$ 第二大特征值 $\lambda_2 $ 对应的特征向量。 s.t.$(w^2)^Tw^2=1$
k-D中:
结论:$w$ 就是协方差矩阵 $S$ 前 $k$ 大的特征值对应的特征向量。s.t. $W$ 是正交矩阵。
1-D
Goal:Find $w^1$ to maximum the variance of $z_1$ .
- $\operatorname{Var}\left(z_{1}\right)=\frac{1}{N} \sum_{z_{1}}\left(z_{1}-\overline{z_{1}}\right)^{2}$
- $z_1=w^1\cdot x ,\quad \overline{z_{1}}=\frac{1}{N} \sum_{z_{1}}=\frac{1}{N} \sum w^{1} \cdot x=w^{1} \cdot \frac{1}{N} \sum x=w^{1} \cdot \bar{x}$
- $\operatorname{Var}\left(z_{1}\right)=\frac{1}{N} \sum_{z_{1}}\left(z_{1}-\overline{z_{1}}\right)^{2}=(w^1)^T\operatorname{Cov}(x)w^1$
- $=\frac{1}{N} \sum_{x}\left(w^{1} \cdot x-w^{1} \cdot \bar{x}\right)^{2} $
- $=\frac{1}{N} \sum\left(w^{1} \cdot(x-\bar{x})\right)^{2}$
$a,b$ 是vector:
$(a\cdot b)^2=(a^Tb)^2=a^Tba^Tb$$a^Tb$ 是scalar:
$(a\cdot b)^2 = (a^Tb)^2=a^Tba^Tb =a^Tb(a^Tb)^T=a^Tbb^Ta$
- $=\frac{1}{N} \sum\left(w^{1}\right)^{T}(x-\bar{x})(x-\bar{x})^{T} w^{1}$
- $ = \left(w^{1}\right)^{T}\sum\frac{1}{N}(x-\bar{x})(x-\bar{x})^{T} \ w^{1}$
- $=(w^1)^T\operatorname{Cov}(x)w^1$
令 $S=\operatorname{Cov}(x)$
之前遗留的两个问题:
- $\left|w^1\right|_2=1$ ?
- $w^1\cdot w^2=1$ ?
现在来看第一个问题,为什么要 $\left|w^1\right|_2=1$ ?
现在的目标,变成了 maximum $(w^1)^T S w^1$ ,如果不限制 $\left|w^1\right|_2$ ,让 $\left|w^1\right|_2$ 无穷大,那么 $(w^1)^T S w^1$ 的值也会无穷大,问题无解了。
Goal:maximum $(w^1)^T S w^1$ s.t. $(w^1)^Tw^1=1$
Lagrange multiplier[挖坑] 求解多元变量在有限制条件下的驻点。
构造拉格朗日函数: $g\left(w^{1}\right)=\left(w^{1}\right)^{T} S w^{1}-\alpha\left(\left(w^{1}\right)^{T} w^{1}-1\right)$ ,$\alpha\neq 0$ 为拉格朗日乘数
- $\nabla_{w^1}g=0$ 的值为驻点(会单独写一篇博客来讲拉格朗日乘数)
- $\frac{\partial g}{\partial \alpha}=0$ 为限制函数
对矩阵微分:详情见wiki
scalar-by-vector(scalar对vector微分)

$S$ 是对称矩阵,不是 $w^1$ 的函数,结果用 $w^1$ 表达:$2Sw^1-2\alpha w^1=0$
maximum: $(w^1)^T S w^1=\alpha (w^1)^Tw^1=\alpha$
*Goal:find $w^1$to maximum $\alpha$ *
$\alpha$ 满足等式:$Sw^1=\alpha w^1$
$\alpha$ 是 $S$ 的特征向量,$w^1$ 是 $S$ 对应于特征值 $\alpha$ 的特征向量。
- 关于特征值和特征向量的知识参考:参考下面线代知识
$w^1$ is the eigenvector(特征向量) of the covarivance matrix S corresponding to the largest eigenvalue $\lambda_1$ .
结论:$w^1$ 就是协方差矩阵最大特征值对应的特征向量。
梦回线代QWQ(自己线代学的太差啦 啊这!
特征向量,特征值定义:
$A$ 是n阶方阵,如果存在数 $\lambda$ 和n维非零向量 $\alpha$ ,满足 $A\alpha=\lambda \alpha$ ,
则称 $\lambda$ 为方阵 $A$ 的一个特征值,$\alpha$ 为方阵 $A$ 对应于特征值 $\lambda$ 的一个特征向量。
求解特征向量和特征值:
$A\alpha -\lambda \alpha=(A-\lambda I)\alpha=0$
齐次方程有非零解的充要条件是特征方程 $det(A-\lambda I)=0$ (行列式为0)
- 根据特征方程先求解出 $\lambda$ 的所有值。
- 再根将 $\lambda$ 代入齐次方程,求解齐次方程的解 $\alpha$ ,即为对应 $\lambda$ 的特征向量。
2-D
Goal:find $w^2$ to maximum $(w^2)^TSw^2 $ s.t. $(w^2)^Tw^2=1, (w^2)^Tw^1=0$
- 构造拉格朗日函数: $g\left(w^{2}\right)=\left(w^{2}\right)^{T} S w^{2}-\alpha\left(\left(w^{2}\right)^{T} w^{2}-1\right)-\beta\left(\left(w^{2}\right)^{T} w^{1}-0\right)$
- 对 $w^2$ 求微分,所求点满足等式: $S w^{2}-\alpha w^{2}-\beta w^{1}=0$
- 左乘 $(w^1) ^T$: $(w^1)^TSw^2-\alpha (w^1)^Tw^2-\beta(w^1)^Tw^1=0$
- 已有: $(w^1)^Tw^2=0, (w^1)^Tw^1=1$
- 证明:$ (w^1)^TSw^2=0$
- $\because (w^1)^TSw^2$ 是scalar
- $\therefore (w^1)^TSw^2=((w^1)^TSw^2)^T=(w^2)^TS^Tw^1$
- $\because S^T=S$ (协方差矩阵是对称矩阵)
- $\because Sw^1=\lambda_1 w^1$
- $\therefore (w^1)^TSw^2=(w^2)^TSw^1=\lambda_1(w^2)^Tw^1=0$
- $(w^1)^TSw^2-\alpha (w^1)^Tw^2-\beta(w^1)^Tw^1=0-\alpha\cdot 0-\beta \cdot 1=0$
- $\therefore \beta=0$
- $w^2$ 满足等式:$S w^{2}-\alpha w^{2}=0$
- 和1-D的情况相同:find $w^2$ maximum $(w^2)^TSw^2$
- $(w^2)^TSw^2=\alpha$
- $w^2$ is the eigenvector(特征向量) of the covarivance matrix S corresponding to the largest eigenvalue $\lambda_2$ .
- OVER!
Conclusion
最后解决之前的Q2:$(w^1)^Tw^2=0$ ?
先说明一下$S$ 的性质:
是对称矩阵,对应不同特征值对应的特征向量都是正交的。
(参考1,2)
也是半正定矩阵,其特征值都是非负的。
(参考4,5,6)
其次关于 $W$ 的性质 $ W=\begin{bmatrix}(w^1)^T \\ (w^2)^T \\ ...\end{bmatrix}$ ,易得 $W$ 是orthogonal matrix(正交矩阵)。
所以这是一个约束条件,能让PCA的最优化问题转化为求其特征值的问题。
(具体见下一小节:PCA-decorrelation)
其次 $z=Wx$ ,也因为 $W$ 的正交性质,让 $z$ 的各维度(特征)decorrelation,去掉相关性,降维后的特征相互独立,方便后面generative model的假设。
$S=Cov(x)$ 为实对称矩阵。
实对称矩阵的性质:$A$ 是一个实对称矩阵,对于于 $A$ 的不同特征值的特征向量彼此正交。
正交矩阵的性质:$W^TW=WW^T=I$
$Var(z)=(w^1)^T S w^1\geq 0$ ,方差一定大于等于0 。
半正定矩阵的定义:
实对称矩阵 $A$ ,对任意非零实向量 $X$ ,如果二次型 $f(X)=X^TAX\geq0$ ,
则有实对称矩阵 $A$ 是半正定矩阵。
半正定矩阵的性质:半正定矩阵的特征值都是非负的。
1-D中:
Goal:find $w^1$ to maximum $(w^1)^T S w^1$ s.t.$(w^1)^Tw^1=1$
结论:$w^1$ 就是协方差矩阵 $S$ 最大特征值 $\lambda_1 $ 对应的特征向量。 s.t.$(w^1)^Tw^1=1$
2-D中:
Goal:find $w^2$ to maximum $(w^2)^TSw^2 $ s.t. $(w^2)^Tw^2=1, (w^2)^Tw^1=0$
结论:$w^2$ 就是协方差矩阵$S$ 第二大特征值 $\lambda_2 $ 对应的特征向量。 s.t.$(w^2)^Tw^2=1$
k-D中:
结论:$w$ 就是协方差矩阵 $S$ 前 $k$ 大的特征值对应的特征向量。s.t. $W$ 是正交矩阵。
PCA-decorrelation
$z=Wx$
通过PCA找到的 $W$ ,$x$ 得到新的presentation $z$ ,如下图。
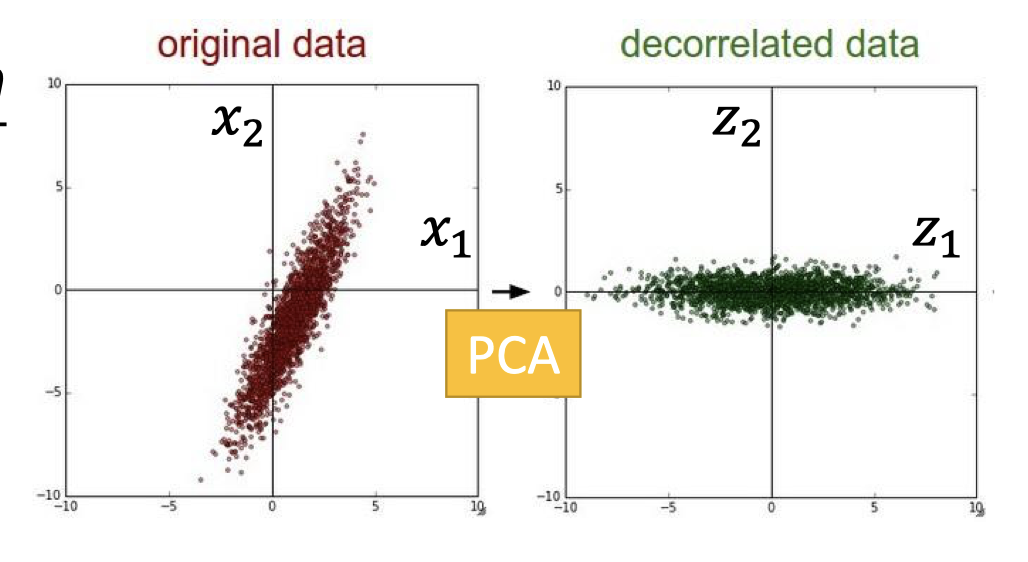
可见,经过PCA后,original data变为decorrelated data,各维度(feature)是去相关性的,即各维度是独立的,方便generative model的假设(比如Gaussian distribution).
$z$ 是docorrelated,即 $Cov(z)=D$ 是diagonal matrix(对角矩阵)
证明:$Cov(z)=D$ is diagonal matrix
- $W=\begin{bmatrix}(w^1)^T \\ (w^2)^T \\ ...\end{bmatrix}$ ,$S=\operatorname{Cov}(x)$
- $\operatorname{Cov}(z)=\frac{1}{N} \sum(z-\bar{z})(z-\bar{z})^{T}=W S W^{T}$
- $=W S\left[\begin{array}{lll}w^{1} & \cdots & w^{K}\end{array}\right]=W\left[\begin{array}{lll}S{w}^{1} & \cdots & S w^{K}\end{array}\right]$
- $=W\left[\lambda_{1} w^{1} \quad \cdots \quad \lambda_{K} w^{K}\right]=\left[\lambda_{1} W w^{1} \quad \cdots \quad \lambda_{K} W w^{K}\right]$ ($\lambda$ is scalar)
- $=\left[\begin{array}{lll}\lambda_{1} e_{1} & \cdots & \lambda_{K} e_{K}\end{array}\right]=D$ ($W$ is orthogonal matrix)
PCA-Another Point of View
Main Idea: Component
PCA看作是一些basic component的组成,如下图,手写数字都是一些基本笔画组成的,记做 $\{u^1,u^2,u^3,...\}$

因此,下图的”7”的组成为 $\{u^1,u^3,u^5\}$
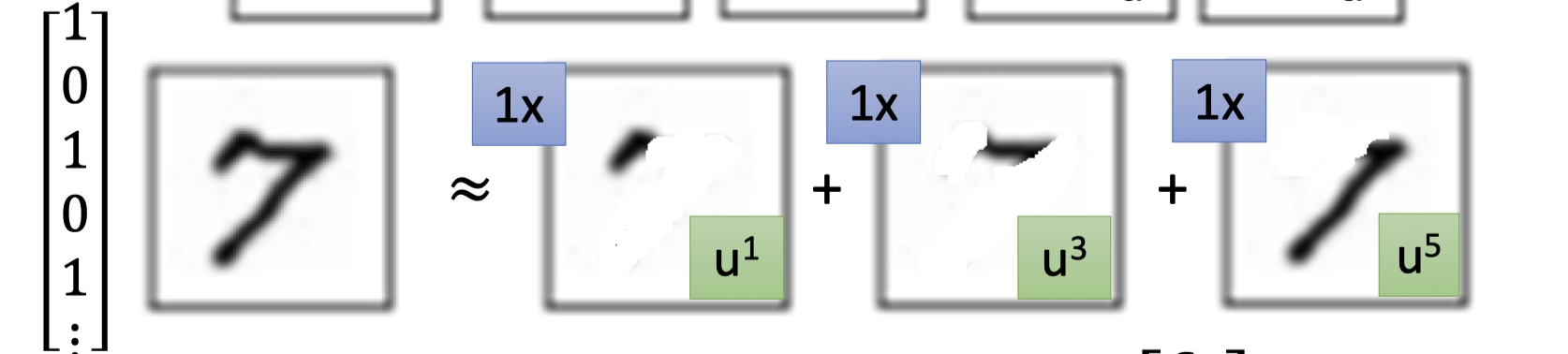
所以原28*28 vector $x$ 表示的图像能近似表示为:
$$ x \approx c_{1} u^{1}+c_{2} u^{2}+\cdots+c_{K} u^{K}+\bar{x} $$其中 $\{u^1,u^2,u^3,...\}$ 是compoment的vector表示, $\{c^1,c^2,c^3,...\}$ 是component的系数,$\bar{x}$ 是所有images的平均值。
因此 $\begin{bmatrix}c_1 \\c_2 \\... \\ c_k \end{bmatrix}$ 也能表示一个数字图像。
现在问题是找到这些component $\{u^1,u^2,u^3,...\}$ , 再得到 他的线形表出 $\begin{bmatrix}c_1 \\c_2 \\... \\ c_k \end{bmatrix}$ 就是我们想得到的better presentation.
Detail
要满足:$x \approx c_{1} u^{1}+c_{2} u^{2}+\cdots+c_{K} u^{K}+\bar{x}$
即,$x -\bar{x}\approx c_{1} u^{1}+c_{2} u^{2}+\cdots+c_{K} u^{K}$ ,等式两边的误差要尽量小。
问题变成:找 $\{u^1,u^2,u^3,...\}$ minimize the reconstruction error = $\|(x-\bar{x})-\hat{x}\|_2$ .
损失函数: $L=\min _{\left\{u^{1}, \ldots, u^{K}\right\}} \sum\left\|(x-\bar{x})-\left(\sum_{k=1}^{K} c_{k} u^{k}\right)\right\|_{2}$
而求解PCA的过程就是在minimize损失函数 $L$ ,PCA中求解出的 $\{w^1,w^2,...,w^K\}$ 就是这里的component $\{u^1,u^2,...,u^K\}$ .(Proof 见Bisho, Chapter 12.1.2)
*Goal: minimize the reconstruction error = $\|(x-\bar{x})-\hat{x}\|_2$ *
$x -\bar{x}\approx c_{1} u^{1}+c_{2} u^{2}+\cdots+c_{K} u^{K}$
每个sample: $\left\{ \begin{matrix} x^{1}-\bar{x} \approx c_{1}^{1} u^{1}+c_{2}^{1} u^{2}+\cdots \\ x^{2}-\bar{x} \approx c_{1}^{2} u^{1}+c_{2}^{2} u^{2}+\cdots \\x^{3}-\bar{x} \approx c_{1}^{3} u^{1}+c_{2}^{3} u^{2}+\cdots \\ ...\end{matrix} \right.$
下图中 $X=x-\bar{x}$ 矩阵的第一列都和上面的 $x^1-\bar{x}$ 对应:
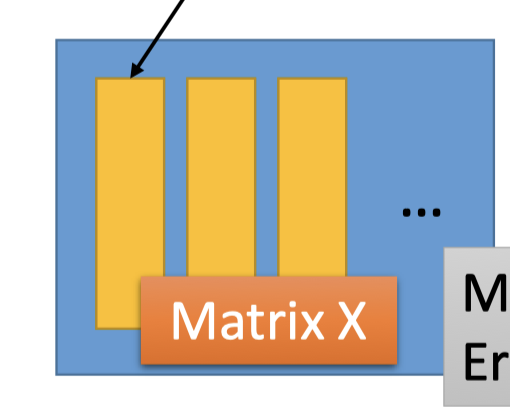
而上面的 $c_{1}^{1} u^{1}+c_{2}^{1} u^{2}+\cdots$ 和下图的component矩阵乘系数矩阵的第一列对应:
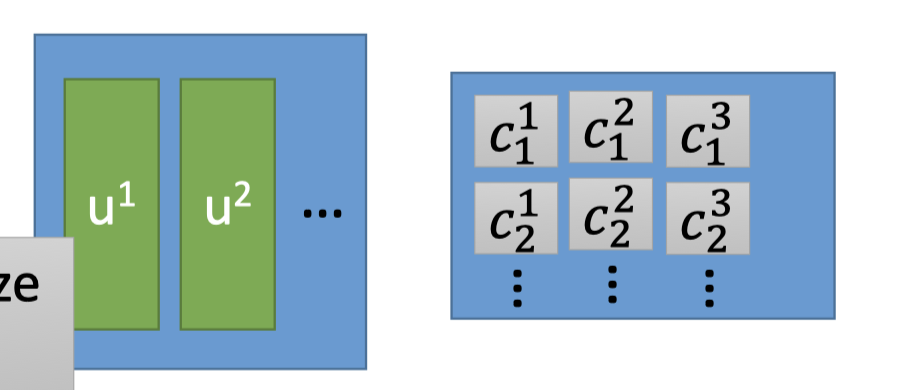
因此,是要让下图矩阵的结果 minimize error:
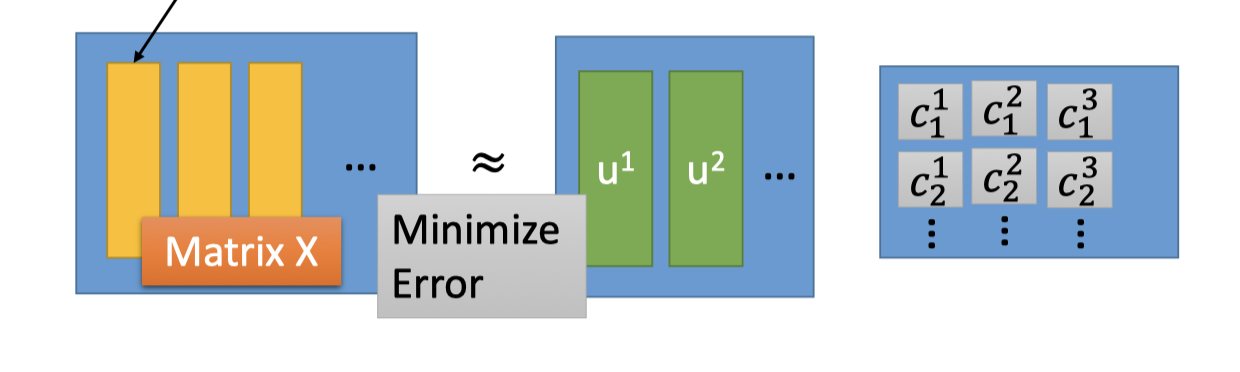
如何求解: SVD矩阵分解-其实就是最大近似分解(挖坑)
SVD能将一个任意的矩阵,分解为下面三个矩阵的乘积。
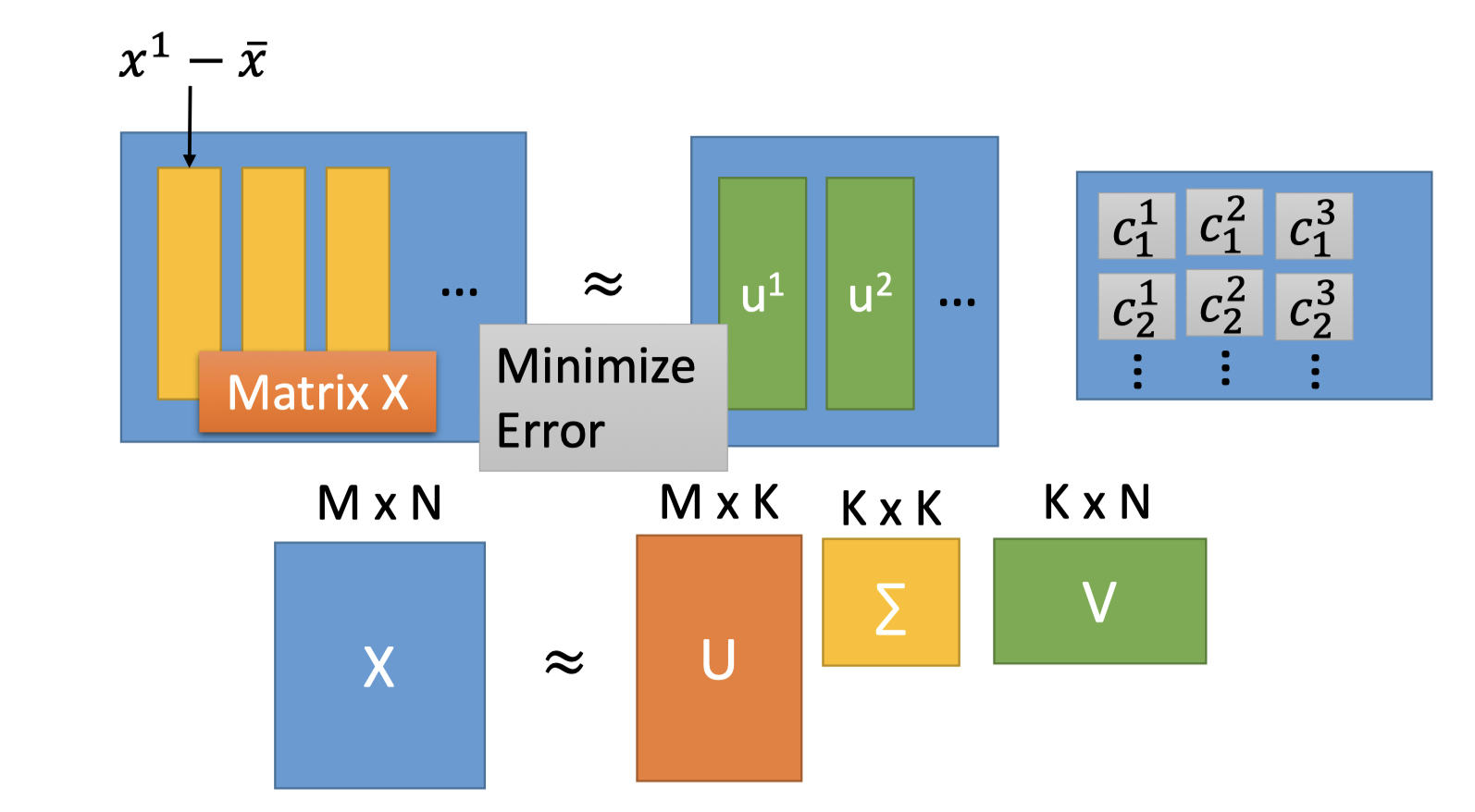
$X = U\Sigma V$
- $U,V$ 都是orthogonal matrix,$\Sigma$ 是diagonal matrix。
- 组成$U$ (M*K) 的K个列向量是 $XX^T$ 矩阵的前K大特征值对应的特征向量。
- 组成 $V$ (K*N)的K个行向量是 $X^TX$ 矩阵的前K大特征值对应的特征向量。
- $XX^T$ 和 $X^TX$ 的特征值相同
- $\Sigma$ 的对角值 $\sigma_i=\sqrt{\lambda_i}$
解:$U$ 矩阵作为 component矩阵, $\Sigma V$ 乘在一起作为系数矩阵。
$U=\{u^1,u^2,u^3,...\}$ 矩阵是$XX^T$ 的特征向量组成正交矩阵。
而PCA的解 $W^T=\{w^1,w^2,...,w^K\}$ 也是特征向量组成的正交矩阵。
所以和PCA的关系:$U$ 矩阵是 $XX^T=Cov(x)$ 的特征向量,所以$U$ 矩阵就是PCA的解。
PCA-NN:Autoencoder
上文说到求解PCA的解 $\{w^1,w^2,...,w^K\}$ 就是在最小化restruction error $x -\bar{x}\approx \sum_{k=1}^K c_kw^k$ .
两者的联系就是PCA的解 $\{w^1,w^2,...,w^K\}$ 就是component $\{u^1,u^2,u^3,...\}$ ,且PCA的表示是 $z$ 对应这里的 $c_k$ (第k个image的表示).
PCA视角: $z=c_k=(x-\bar{x})\cdot w^k$
PCA looks like a neural network with one hidden layer(linear activation function)。
把PCA视角看作一个NN,如下图,其hidden layer的激活函数是一个简单的线性激活函数。
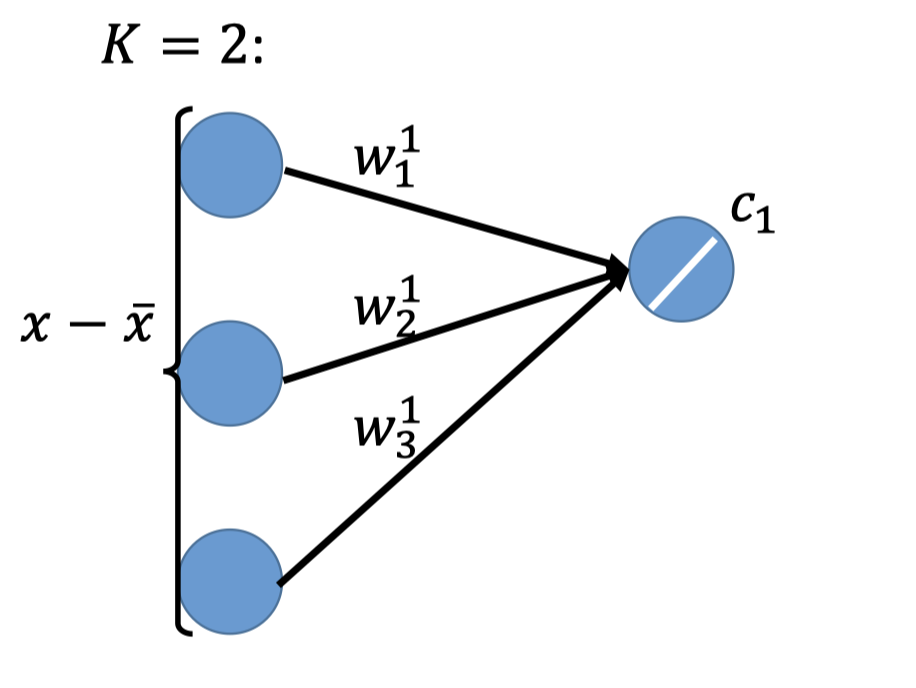
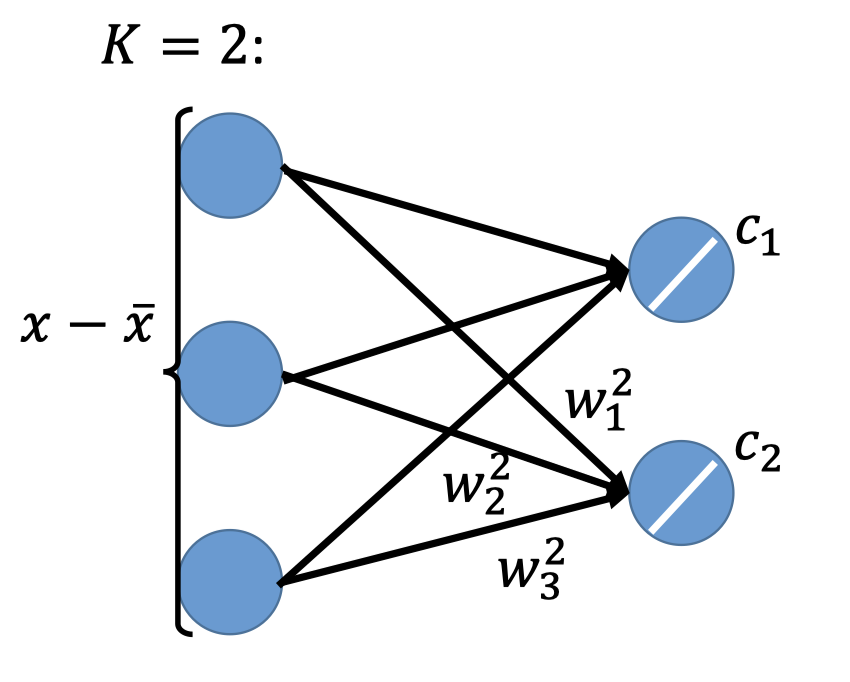
再看component视角: $\hat{x}=\sum_{k=1}^K c_kw^k\approx x-\bar{x}$
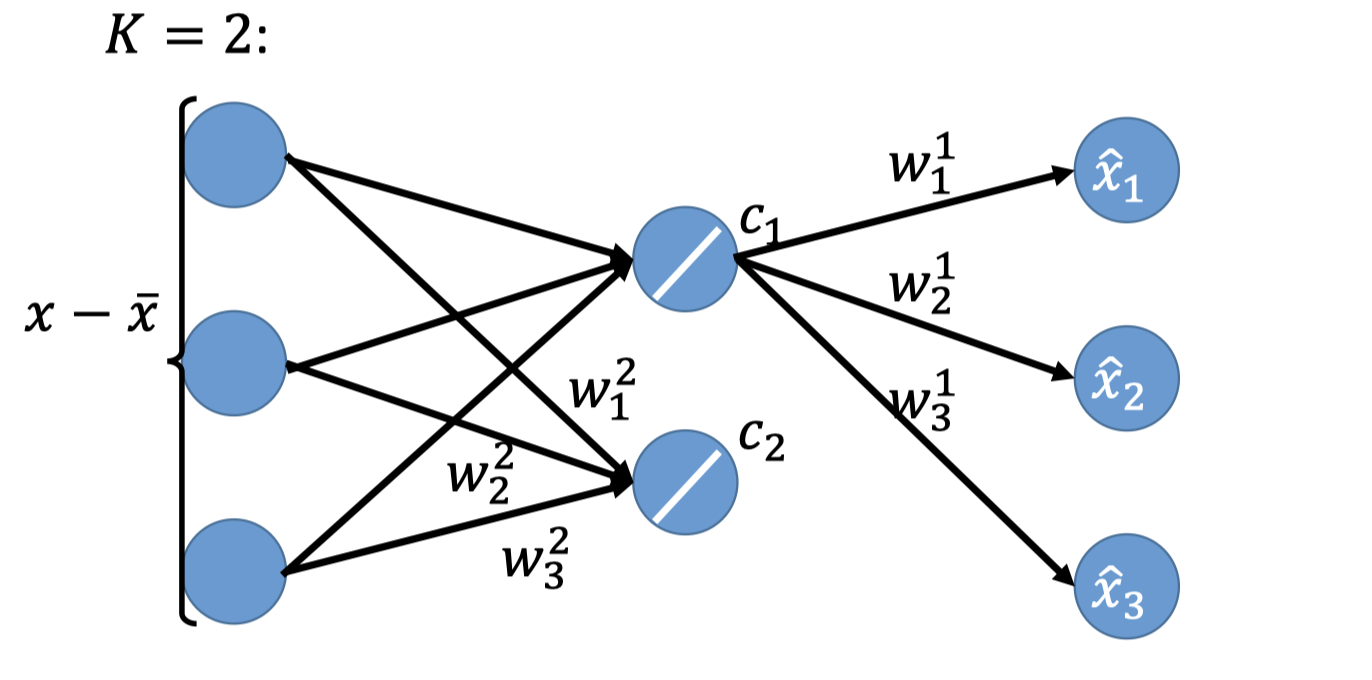
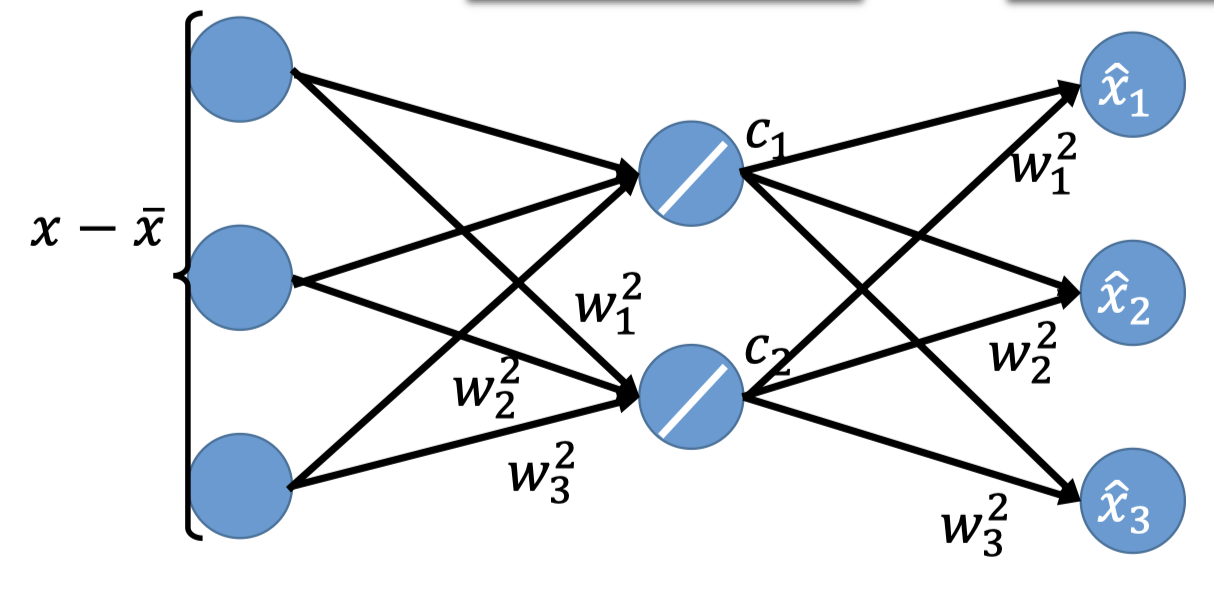
PCA就构成了下面的NN,hidden layer可以是deep,这就是autoencoder(后面的博客会再详细讲)。
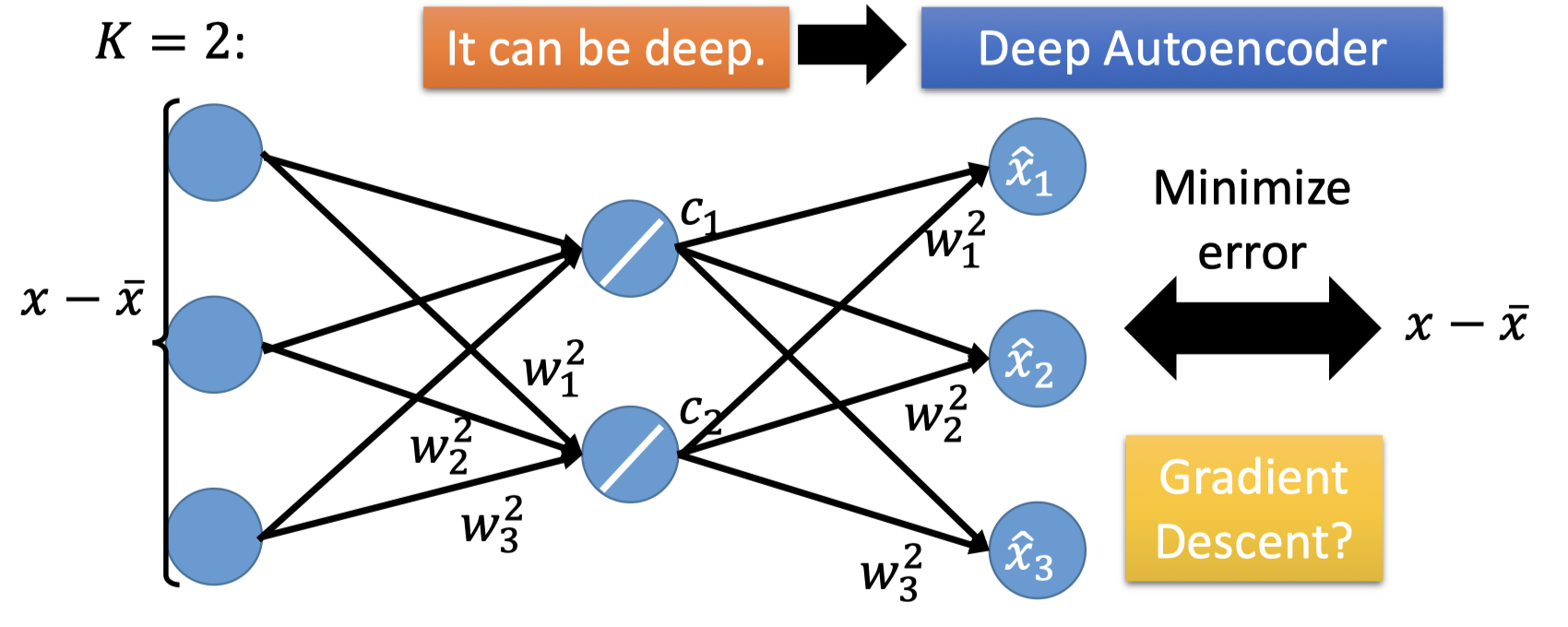
用Gradient Descent对输入输出做minimize error,hidden layer的输出 $c$ 就是我们想要的编码(降维后的编码)。
Q:用PCA求出的结果和用Gradient Descent训练NN的结果一样吗?
A:当然不一样,PCA的 $w$ 都是正交的,而NN的结果是gradient descent迭代出来的,并且该结果还会于初值有关。
Q:有了PCA,为什么还要用NN呢?
A:因为PCA只能处理linear的情况,对前文那种高维的非线形的无法处理,而NN可以是deep的,能较好处理非线形的情况。
tips: how many components?
比如在对Pokemon进行PCA时,有六个features,如何确定principle component的数目?
往往在实际操作中,会对每个component计算一个ratio,如图中的公式:

因为每一个component对应一个eigenvector,每个eigenvector对应一个eigenvalue,而这个eigenvalue的值代表了在这个component的维度的variance有多大,越大当然能更好的表示。
因此计算eigenvalue的ratio,来找出分布较大的component作为主成分。
More About PCA
如果对MNIST做PCA分析,结果如下图,会发现下面eigen-digits这些并不像数字的某个组成部分:

同样,对face做PCA分析,结果下图:
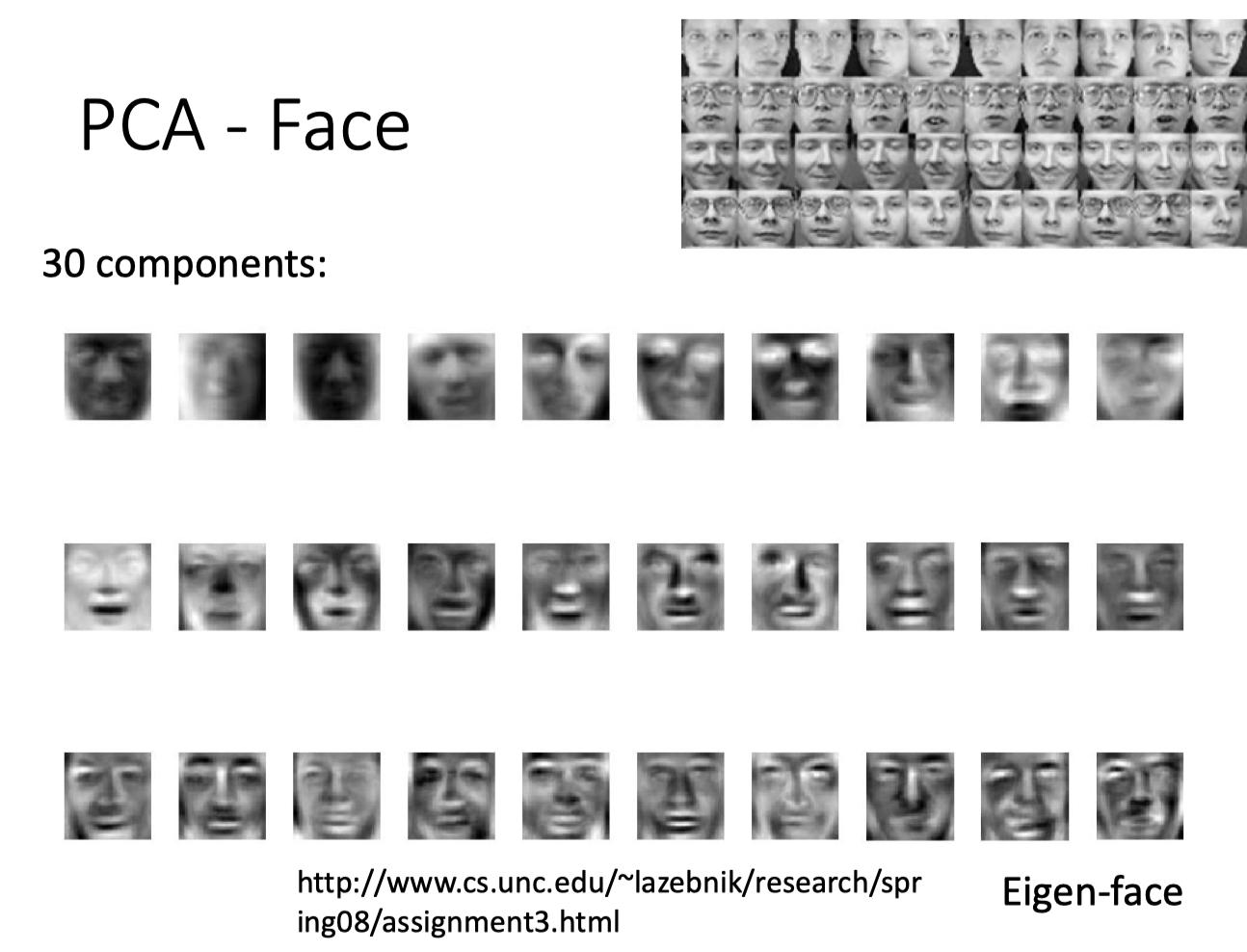
为什么呢?
在MNIST中,一张image的表示如下图:
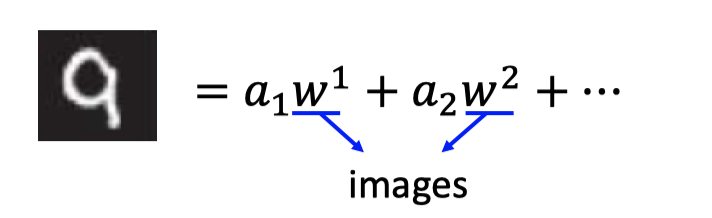
其中,$\alpha$ 可以是任意实数,那么就有正有负,所以PCA的解包含了一些真正component的adding up and subtracting,所以MNIST的解不像这些数字的一部分。
如果想得到的解看起来像真正的component,可以规定图像只能是加,即 $\alpha$ 都是非负的。
- Non-negative matrix factorization(NMF)
- Forcing $\alpha$ be non-negative: additive combination
- Forcing $w$ be non-negative: components more like “parts of digits”
Weakness of PCA
PCA是unsupervised,因此可能不能区分本来是两个类别的东西。
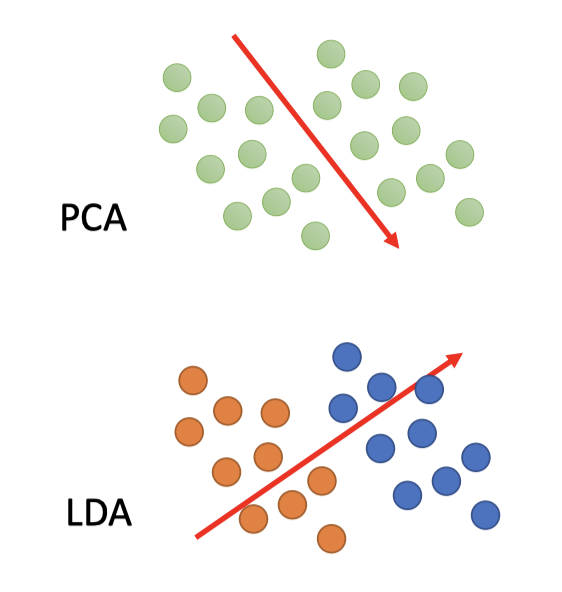
如图,PCA的结果可能是上图的维度方向,但如果引入labeled data,更好的表达应该按照下图LDA的维度方向。
- LDA (Linear Discriminant Analysis) 是一种supervised的分析方法。
PCA是Linear的,前文已经提及过,除了可以用NN的方式也有很多其他的non-linear的解法。
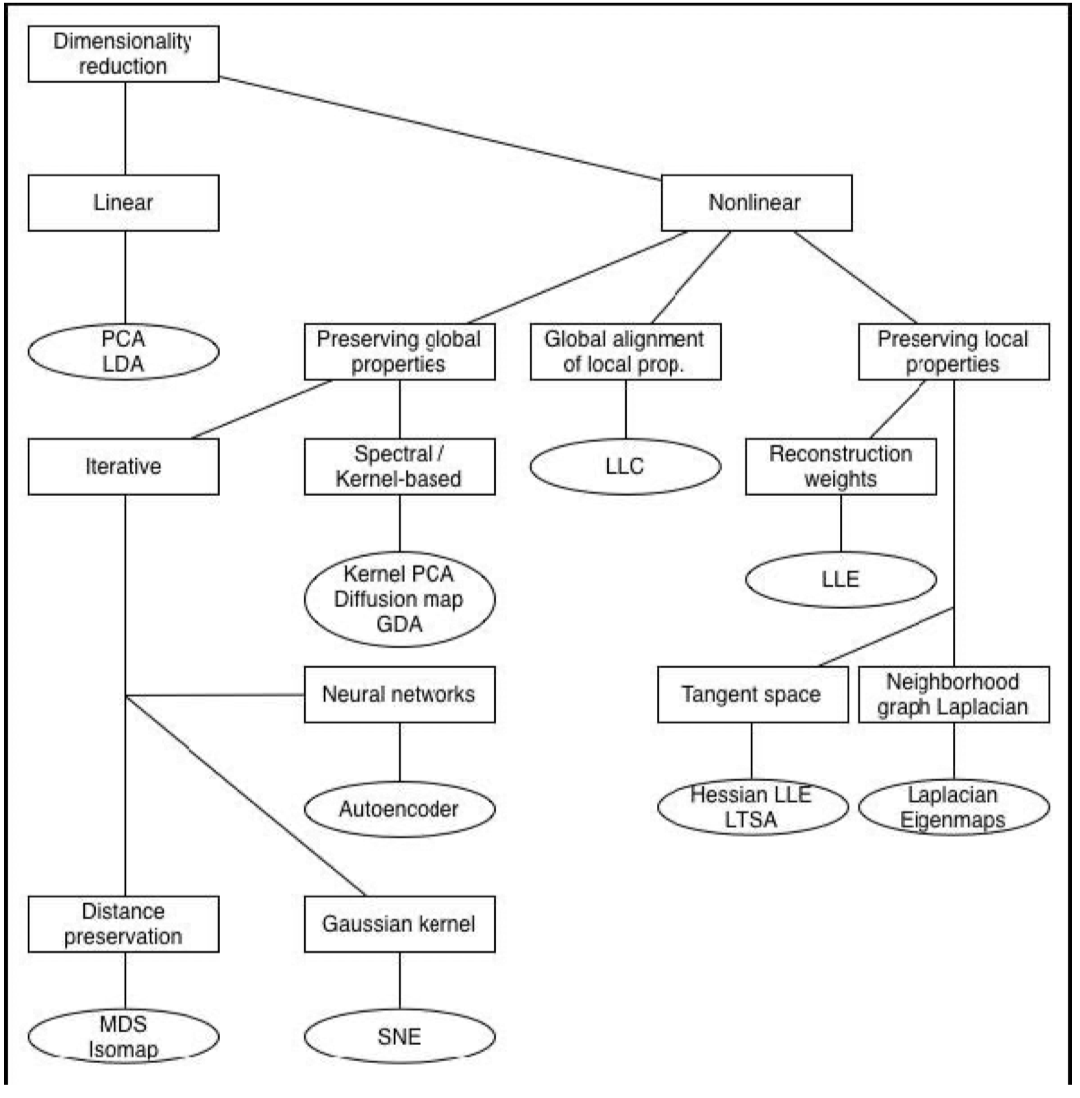
Reference
HAC的算法细节待补充完善:https://zhuanlan.zhihu.com/p/34168766
PCA: Bishop, Chapter12.
线代知识:特征值、特征向量、实对称矩阵等:
拉格朗日乘数:Bishop, Appendix E
矩阵微分:https://en.wikipedia.org/wiki/Matrix_calculus#Derivatives_with_vectors
Proof-PCA的过程就是在minimize损失函数 $L$ :Bisho, Chapter 12.1.2
SVD:
NMF:Non-negative matrix factorization
LDA:Linear Discriminant Analysis
「机器学习-李宏毅」:Unsupervised-PCA

