「Cryptography-Boneh」:Collision Resistance
上一节介绍了基于PRFs的MAC构造和基于随机的MAC:

本节我们将介绍抗碰撞的MAC(MACs from collision resistance)。
第一部分介绍了什么是抗碰撞 (Collision Resistance),以及基于C.R.的MAC的安全性。
第二部分介绍了生日悖论,如何用生日攻击寻找2-way collision 和3-way collision.
第三部分介绍了Merkle-Damgarg范式(如果压缩函数h是C.R.,那么构造出的哈希函数H就是C.R.)以及如何构建C.R.的压缩函数(Davies-Meyer压缩函数).
最后一部分介绍了HMAC (Hash MAC)和一种针对MAC验证的timing attack and defense.
Collision Resistance
Let H: M →T be a hash function (|M|>>|T|)
【H是一个哈希函数】
A collision for H is a pair $\mathrm{m_0,m_1\in M}$ such that:
$$ \mathrm{H(m_0)=H(m_1)\quad and\quad m_0\ne m_1} $$【哈希碰撞是指,存在两个不同的消息,其哈希函数的值相等。】
A function is collision resistant if for all (explicit) “eff” algs. A:
$$ \operatorname{Adv}_{\mathrm{CR}}[\mathrm{A}, \mathrm{H}]=\operatorname{Pr}[\text { A outputs collision for } \mathrm{H}] \quad \text{is "neg."} $$【如果对于所有多项式时间算法,输出哈希函数H的碰撞的概率是可忽略的,就说明哈希函数H是抗碰撞的(collision resistant),比如SHA-256就是一个抗碰撞的哈希函数。】
MACs from C.R.
如何从抗碰撞的哈希函数构建MACs?
Let I = (S,V) be a MAC for short messages over (K,M,T) (e.g. AES)
Let $\mathrm{H}: \mathrm{M}^{\mathrm{big}} \rightarrow \mathrm{M}$
Def: $\mathrm{I}^{\mathrm{big}}=\left(\mathrm{S}^{\mathrm{big}}, \mathrm{V}^{\mathrm{big}}\right)$ over $\left(\mathrm{K}, \mathrm{M}^{\mathrm{big}}, \mathrm{T}\right)$ as:
$$
\begin{align}
\mathrm{S}^{\mathrm{big}(k, m)}=&\mathrm{S}(k, \mathrm{H}(m)) \ \mathrm{V}^{\mathrm{big}}(k, m, t)=&\mathrm{V}(k, \mathrm{H}(m), t)
\end{align}
$$
【I是一个针对短消息的MAC算法,H是一个哈希函数,能将极大的消息映射到较短的消息空间上。】
Thm :
If I is a secure MAC and H is collision resistant then $\mathrm{I^{big}}$ is a secure MAC.
【如果I是一个secure MAC,并且H是抗碰撞的,$\mathrm{I^{big}}$ 就是一个secure MAC】
其中,Collision resistence 是满足安全的必要条件:
假设攻击者可以找到一个碰撞:$\mathrm{m_0\ne m_1\quad s.t. H(m_0)=H(m_1)}$
那么,$\mathrm{I^{big}}$ 在1-chosen msg 攻击下就是不安全的:
- 攻击者请求得到tag: $\mathrm{t} \longleftarrow \mathrm{S}\left(\mathrm{k}, \mathrm{m}_{0}\right)$
- 伪造pair $\mathrm{(m_1,t)}$ 作为输出
Generic birthday attack
Generic attack on C.R. functions
$\mathrm{H}: \mathrm{M} \rightarrow{0,1}^{\mathrm{n}}$ 是一个哈希函数.$\left(|M| \gg 2^{n}\right)$
一般的攻击算法可以在 $\mathcal{O}(2^{n/2})$ 时间内找到一对哈希碰撞:
- 在M中随机选择 $2^{n/2}$ 不同的消息:$\mathrm{m_1,\dots,m_{2^{n/2} } }$
- for i = 1, …, $2^{n/2}$ ,计算出其对应的哈希值: $\mathrm{t}_{\mathrm{i}}=\mathrm{H}\left(\mathrm{m}_{\mathrm{i}}\right) \quad \in\{0,1\}^{\mathrm{n}}$
- 查看这其中是否有碰撞(即满足 $\mathrm{t_i=t_j}$ ),如果没有,返回第一步。
(只需要进行很少迭代,就可以找到碰撞)
The birthday paradox
为什么上述算法有效?
生日悖论告诉我们,如果 $r_{1}, \ldots, r_{n} \in{1, \ldots, B}$ 是独立同分布的变量(均匀分布是最坏的情况),当 $n=1.2 \times B^{1 / 2}$ 时,存在碰撞 $r_i=r_j(i\ne j)$ 的概率大于等于1/2。
Let $r_{1}, \ldots, r_{n} \in{1, \ldots, B}$ be indep. identically distributed integers.
Thm : when $n=1.2 \times B^{1 / 2}$ then $\operatorname{Pr}\left[\exists \mathrm{i} \neq \mathrm{j}: \mathrm{r}_{\mathrm{i}}=\mathrm{r}_{\mathrm{j}}\right] \geq 1 / 2$ .
Proof: (for uniform indep. $r_{1}, \ldots, r_{n} $)
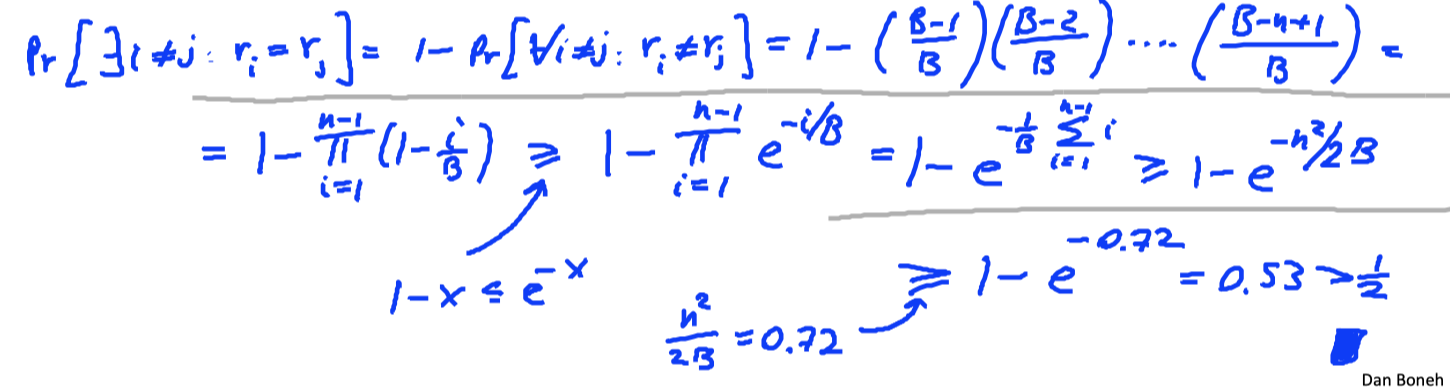
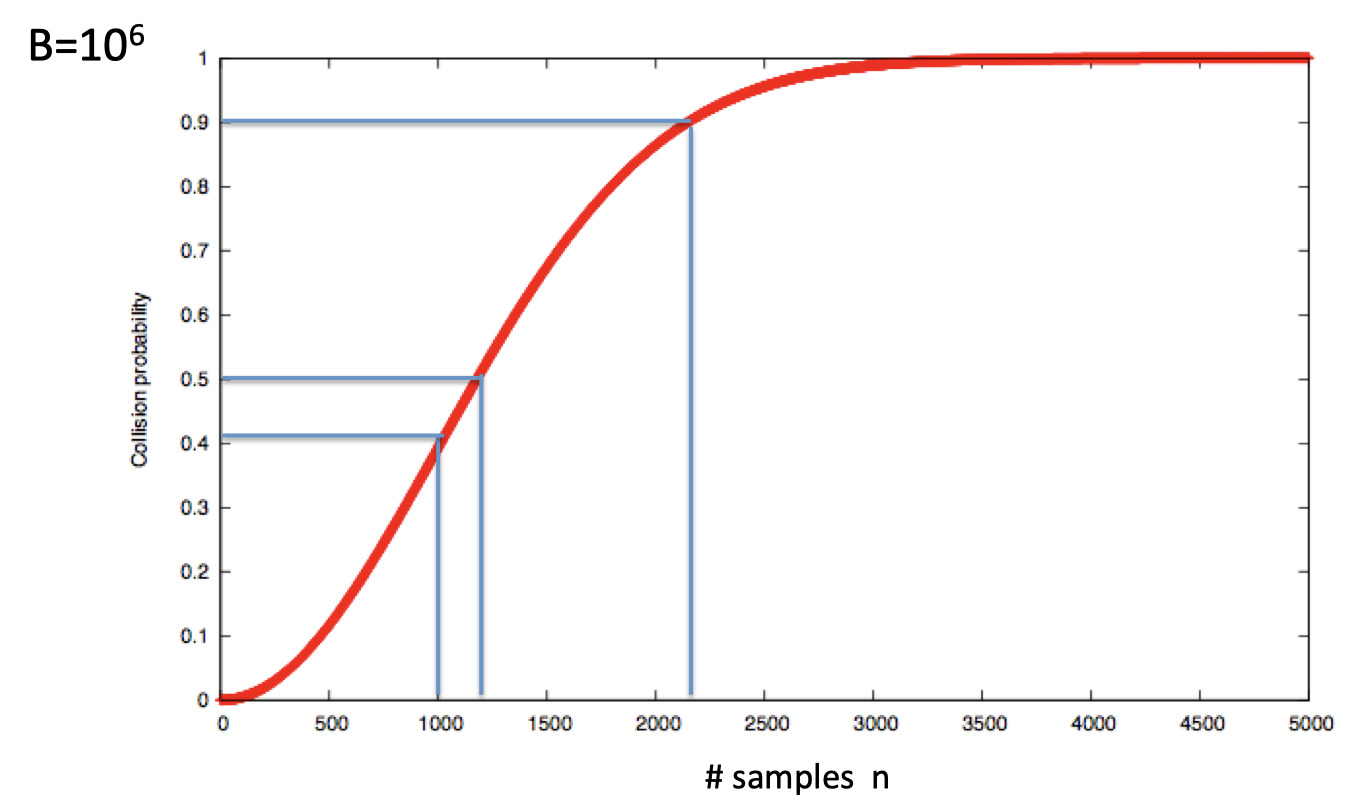
取样数n和碰撞概率的关系如图:
因此上述的攻击算法只需要迭代两次,就能以极大的概率找到碰撞。其时间、空间复杂度都为 $\mathcal{O}(2^{n/2})$
Sample C.R. hash functions
抗碰撞哈希函数的比较:

因此SHA-1的digest size太小,可以很容易的找到碰撞,所以不推荐使用。
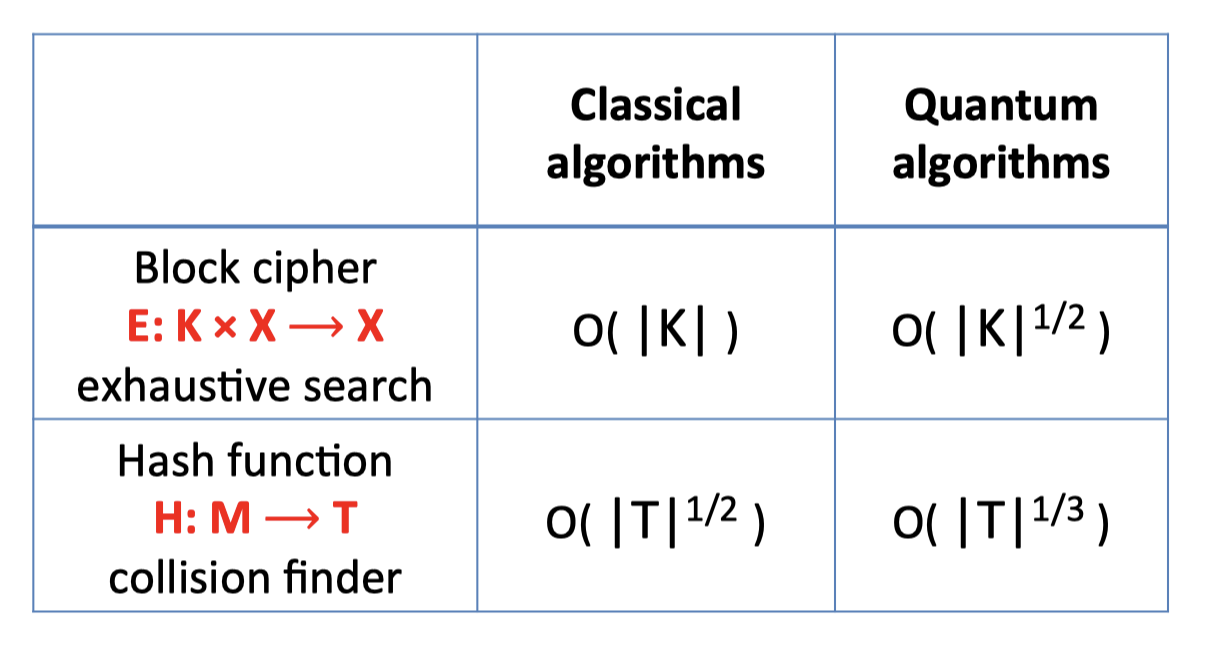
不管量子计算机能大幅降低寻找碰撞的时间:
Three way collision
简化考虑two-way collision:
哈希函数 $\mathrm{H}: \mathrm{M} \rightarrow \mathrm{T\quad(|T|=t)} $ ,应该随机取样$n$个不同的数字,才能以极大的概率找到碰撞满足 $H(y)=H(x)$ .
- n个不同的数字中,有 $n\times(n-1)$ 个pair$(x, y)$ .
- 而对于任意值$H(x)$,$y$满足 $H(y)=H(x)$ 的概率为 $1/t$ .
- 因此应该满足: $n^2=t$
即只需要取样 $\mathcal{O}(|T|^{1/2})$ 个值,即可找到碰撞。
同理,考虑three-way collision:
哈希函数 $\mathrm{H}: \mathrm{M} \rightarrow \mathrm{T\quad(|T|=t)} $ ,应该随机取样$n$个不同的数字,才能以极大的概率找到碰撞满足 $H(x)=H(y)=H(z)$ .
- n个不同的数字中,有 $\frac{n\times(n-1)\times(n-2)}{3!}$ 个pair $(x,y,z)$ .
- 而对于任意值H(x),y和z满足 $H(y)=H(z)=H(x)$ 的概率为 $1/t^2$
- 因此应该满足:$n^3/6 = t^2$
所以只需要取样 $\mathcal{O}(|T|^{2/3})$ 个值,即可找到碰撞。
The Merkle-Damgard Paradigm
The MD iterated construction
通过压缩函数(compression function) $\mathrm{h: T \times X \rightarrow T}$ ,我们可以得到哈希函数 $\mathrm{H}: X^{\leq L} \longrightarrow T$ .
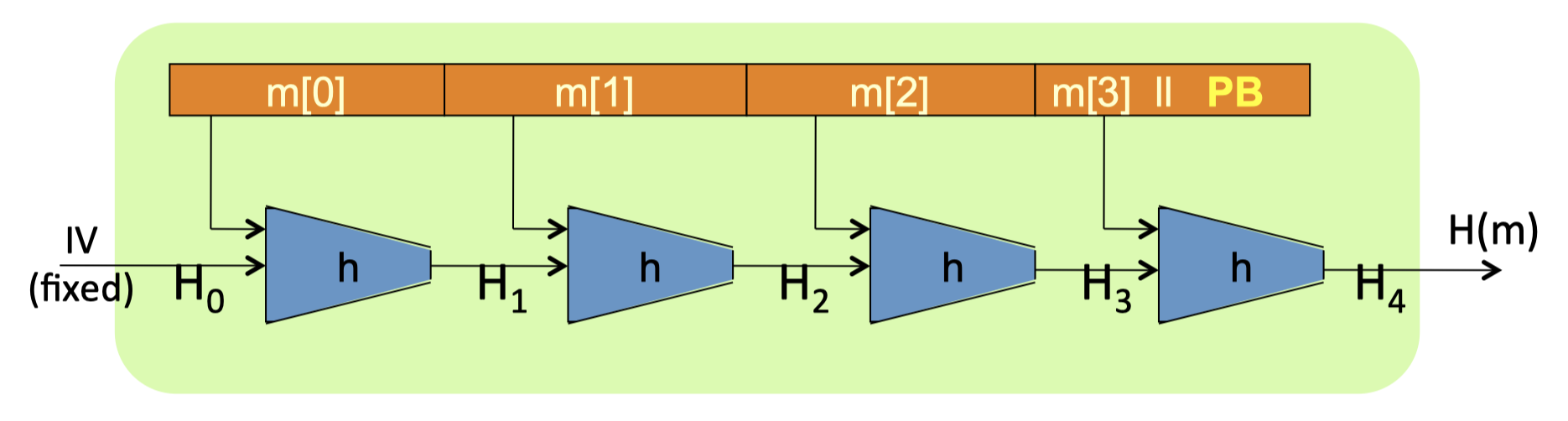
$\mathrm{H_i}:$ chaining variables
$\mathrm{PB}:$ padding block (If no space for PB add another block).

MD collision resistance
上述构造是抗哈希的。
Thm: If h is collision resistant then so is H.
【如果压缩函数h是抗哈希的,那么构造出的哈希函数也是抗哈希的】
Proof: collision on H $\Rightarrow$ collision on h
【通过反证法证明,如果能找到H的碰撞,那么也能找到h压缩函数的碰撞】
假设 $\mathrm{H(M)=H(M’)}$ ,我们可以尝试构造出h的碰撞。
【1】只需要最后一块满足:$\mathrm{h\left(H_{t}, M_{t} | P B\right)=H_{t+1}=H_{r+1}^{\prime}=h\left(H_{r}^{\prime}, M_{r}^{\prime} | P B^{\prime}\right)}$ .
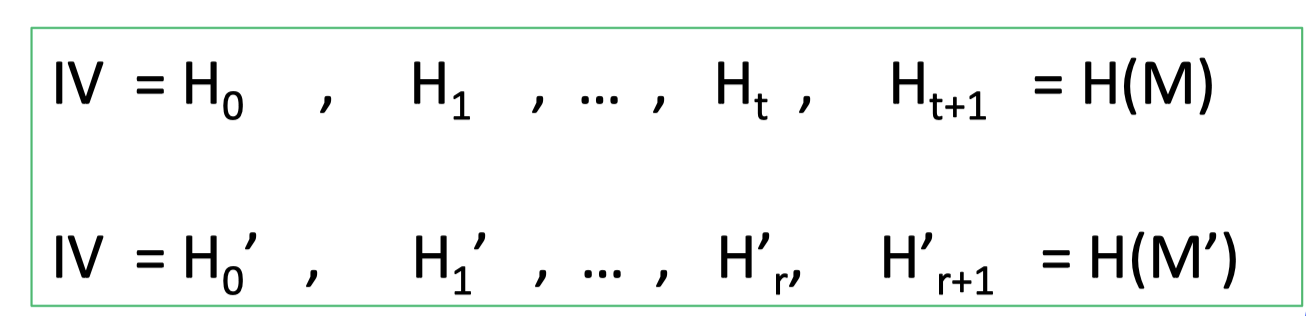
【1】如果h函数的参数不完全相同,那么就找到了h的碰撞
即 $\mathrm{H_t\ne H_r’}$ or $ \mathrm{M_t\ne M_r’}$ or $\mathrm{PB\ne PB’}$ .【2】否则:如果 $\mathrm{H_t= H_r’}$ and $ \mathrm{M_t= M_r’}$ and $\mathrm{PB= PB’}$ (可以得出 $t=r$ )
满足式子:$\mathrm{h\left(H_{t-1}, M_{t-1} \right)=H_{t}=H_{t}^{\prime}=h\left(H_{t-1}^{\prime}, M_{t-1}^{\prime} \right)}$ .【2】同样的,如果h函数的参数不完全相同,就找到了一个h的碰撞:
即 $\mathrm{H_{t-1}\ne H_{t-1}’}$ or $ \mathrm{M_{t-1}\ne M_{t-1}’}$ .
【*】因此通过迭代的方式,到最后:
- 要么找到h压缩函数的碰撞
- 要么 $\forall i: M_i=M_i’ \Rightarrow M=M’$ ,但这就不满足是H哈希函数的碰撞了。
- 因此,如果能找到H哈希函数的碰撞,就一定能找到h压缩函数的碰撞。
所以,在MD结构中,如果想要构建抗碰撞的哈希函数,就需要先保证压缩函数是抗碰撞的。
Constructing Compression Functions
根据上文MD的定理:如果压缩函数h是抗碰撞的,那么H哈希函数也是抗碰撞的。
因此,本节的目标就是如何构建压缩函数 $\mathrm{h: T \times X \rightarrow T}$
Comp. func. from a block cipher
我们可以从块密码中构建压缩函数。
block cipher: $\mathrm{E}: \mathrm{K} \times{0,1}^{\mathrm{n}} \longrightarrow{0,1}^{\mathrm{n}}$
Davies-Meyer compression function: $\mathrm{h(H, m)=E(m, H) \oplus H}$
【把消息块m作为密钥】
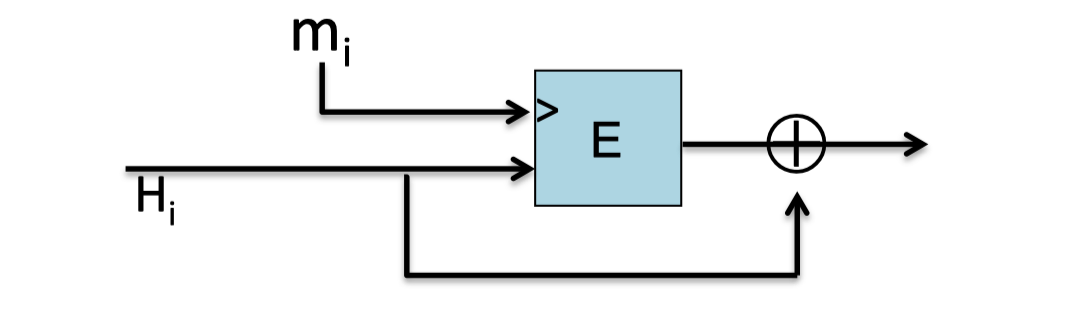
Thm: Suppose E is an ideal cipher (collection of |K| random perms.)
Finding a collision $\mathrm{h(H,m)=h(H’,m’)}$ takes $\mathcal{O}(2^{n/2})$ evaluations of (E, D).
【如果E是一个理想的密码,即每一个密钥都对应一个随机置换,那么通过生日攻击,找到一个碰撞需要 $\mathcal{O}(2^{n/2})$ 次(E, D)的计算。】
如果DM压缩函数是 $\mathrm{h(H, m)=E(m, H)}$ ,函数h就不抗碰撞。
其他通过块密码构建的压缩函数:
简化 $\mathrm{E}:{0,1}^{\mathrm{n}} \times{0,1}^{\mathrm{n}} \rightarrow{0,1}^{\mathrm{n}}$
Miyaguchi-Preneel:
- $\mathrm{h(H, m)=E(m, H) \oplus H \oplus m}$ (Whirlpool)
- $\mathrm{h(H, m)=E(H \oplus m, m) \oplus m}$
- and so on.
同样的,对于这样的变体 $\mathrm{h}(\mathrm{H}, \mathrm{m})=\mathrm{E}(\mathrm{m}, \mathrm{H}) \oplus \mathrm{m}$ 是不安全的。
Case study: SHA-256
SHA-256哈希函数的组成要件:
- Merkle-Damgard function
- Davies-Meyer compression function
- Block cipher: SHACAL-2
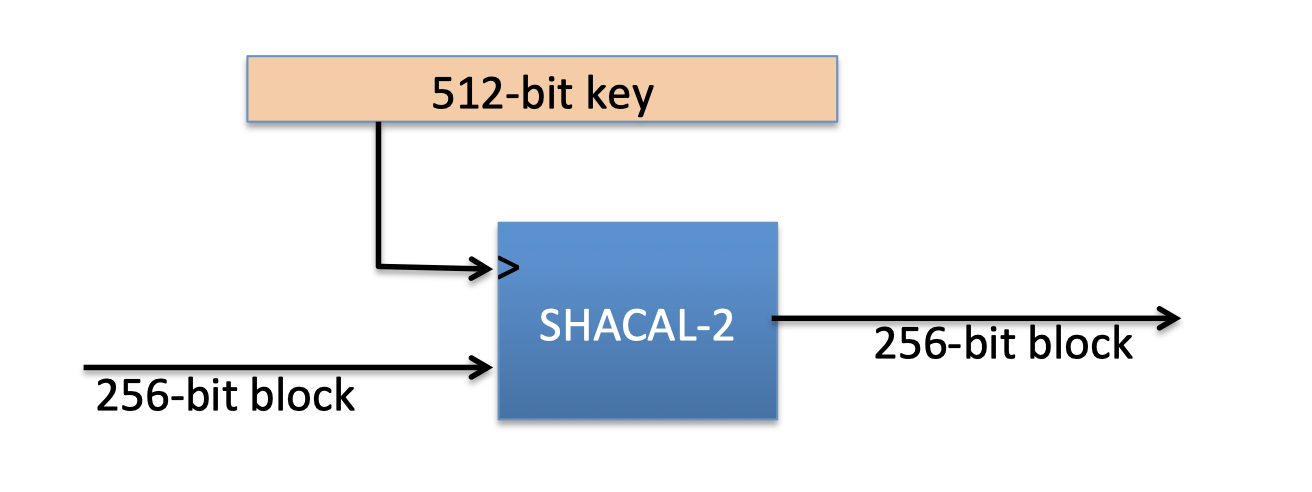
其中512-bit的key是从msg block中截取的,256-bit block是chaining variable.
Provable compression functions
还有一种可证明的压缩函数,即如果你能找到该压缩函数的碰撞,必须解决困难问题。
对于任意 $\mathrm{m}, \mathrm{h} \in{0, \ldots, \mathrm{p}-1}$ ,定义压缩函数 $\mathrm{h(H, m)=u^{H} \cdot v^{m} \quad(\bmod p)}$ .
Fact: finding collision for h(.,.) is as hard as solving “discrete‐log” modulo p.
Problem: slow.
HMAC
通过上述Merkle-Damgard的构造,如果压缩函数h是抗碰撞的,H哈希函数也是抗碰撞的。

那么,我们能否直接使用该哈希函数H(·)构造MAC?
$\mathrm{\mathrm{H}: X^{\leq L} \longrightarrow T}$ a C.R. Merkle-Damgard Hash Function
Attempt: $\mathrm{s(k, m)=H(k | m)}$
这样是不安全的,类似上篇文章中提到的NMAC,如果没有最后一步加密,就是不安全的。
通过Extension Attack ,对给定哈希值 $\mathrm{H(k| m)}$ ,可以计算出任意 $\mathrm{H(k| m|w)}$ .
HMAC: Hash MAC
因此,通过哈希函数构造MAC的标准方法是HMAC(Hash MAC),H是哈希函数,通过不同的哈希函数,该MAC值也有不同的输出长度。比如用SHA-256作为哈希函数,MAC的输出就是256比特。
HMAC可以将任意哈希函数作为黑盒,因此HMAC广泛应用于互联网中的协议。
HMAC:
$$
\mathrm{S}(\mathrm{k}, \mathrm{m})=\mathrm{H}(\mathrm{k} \oplus \mathrm{opad} | \mathrm{H}(\mathrm{k} \oplus \mathrm{ipad} | \mathrm{m}))
$$
(opad: outer pad, 512-bit)
(ipad: inner pad, 512-bit)
HMAC的结构和基于PRF的NMAC结构很像:
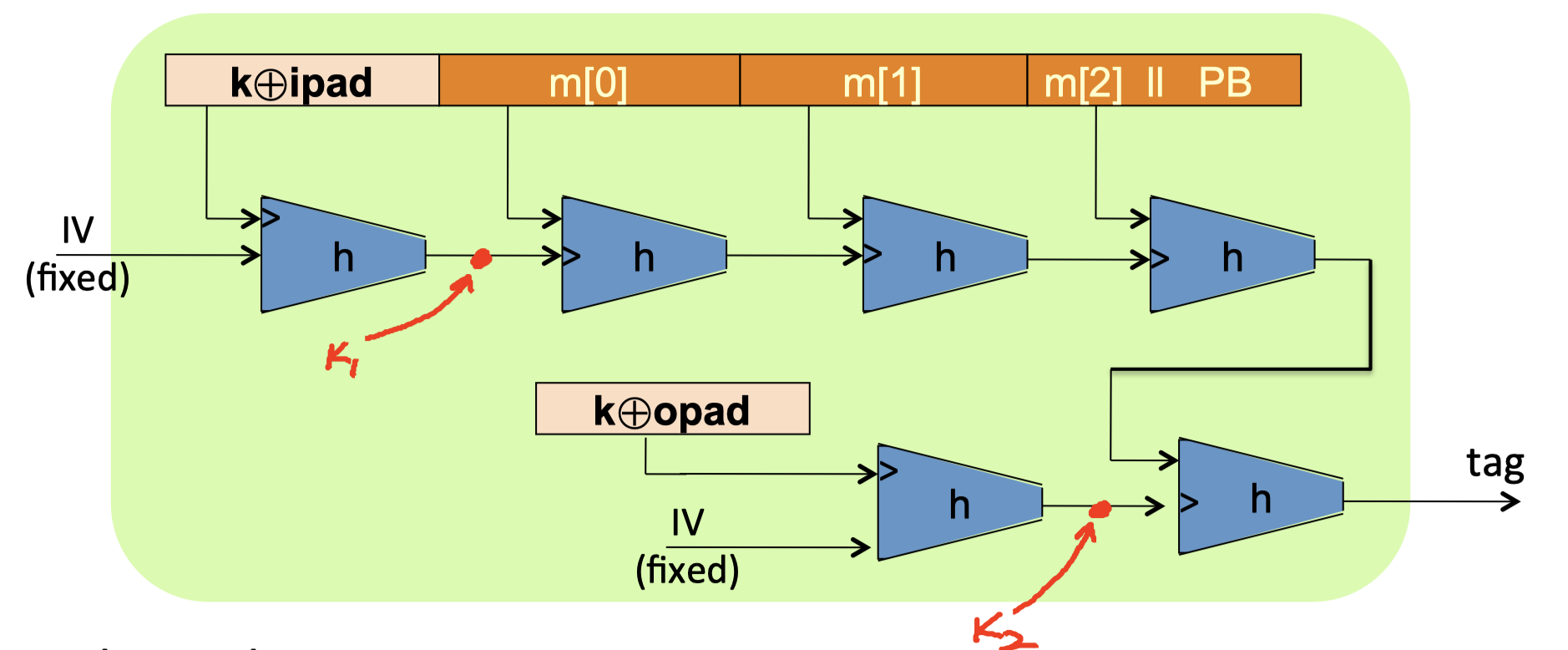
- $\mathrm{h(IV,k\oplus ipad)}$ : 是NMAC的 $\mathrm{k_1}$ .
- $\mathrm{h(IV,k\oplus opad)}$ : 是NMAC的 $\mathrm{k_2}$ .
- 主要的不同点在于,HMAC中的两个密钥 $\mathrm{k_1,k_2}$ 是相关的。
Timing Attacks on MAC Verification
有一种针对MAC验证的时间攻击。
比如在Keyczar crypto library中,验证MAC的函数简化为:

Problem: ‘==’在python中的实现是按字节对比 (byte-by-byte comparison)。
因此,如果对比出了第一个不相等的字节,就会返回false.
Timing Attack
Timing attack: 对目标消息m计算tag

- 向服务器随机请求一个随机tag,记录下验证时间。
- 遍历随机tag的第一个字节,发送给服务器。当验证时间比第一步中的时间略长时,停止,即找到了第一个字节的值。
- 重复tag的所有字节,直到找到最终有效的tag。
保护方法的核心就是:让所有字符串的比较时间都相同。
Defense 1
第一种是要比较完所有字节。

但囿于编译器的优化等因素,这很难实现。
Defense 2
第二种则是通过再次MAC来比较两个字符是否相同。
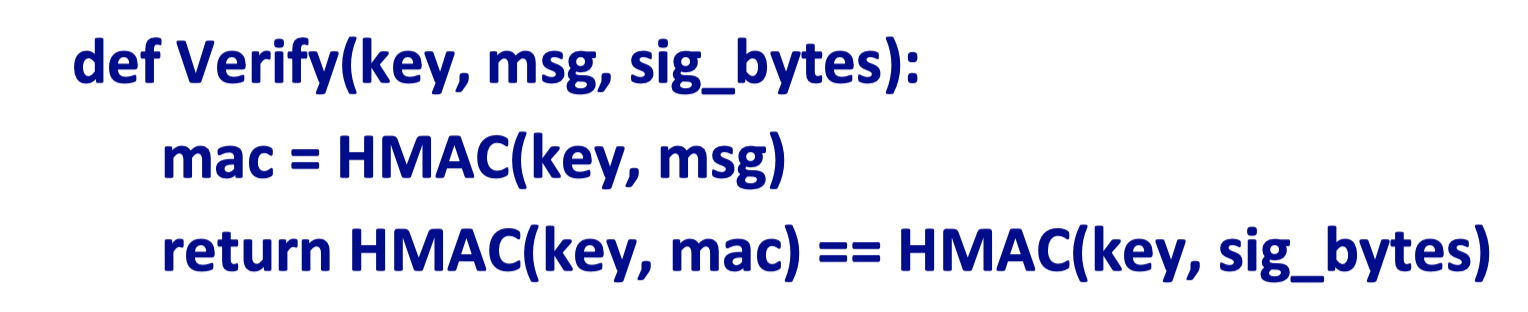
由此可见,密码算法的实现也会让算法变得不安全。
Boneh: Don’t implement crypto yourself!
「Cryptography-Boneh」:Collision Resistance

