「Cryptography-MIT6875」: Lecture 16

In this series, I will learn MIT 6.875, Foundations of Cryptography, lectured by Vinod Vaikuntanathan.
Any corrections and advice are welcome. ^ - ^

Topics Covered:

• IP for Quadratic Non-Residuosity
• Non-interactive ZK
  • NIZK in The Common Random String(CRS) Model
  • Construction in CRS Model: Blum-Feldman-Micali’88 (quadratic residuosity)
  • NIZK for QNR
  • NIZK for 3SAT
• Proofs vs. Argument

At the end of last blog, we said that Non-Interactive Zero-Knowledge (NIZK) is achievable in random oracle model.

Today, we move to the NIZK in the common random string model.

The Power of Interactive Proofs

Before proceeding to NIZK, let’s focus on the power of Interaction Proofs(IP).

Is IP more powerful than NP ?

We have been using interaction to get zero knowledge proofs for NP.

Indeed, interaction is necessary.

But, never mind zero knowledge for a moment.

Can you prove more stuff with interactive proofs than with traditional (i.e. NP) proofs ?

The thing to point is that we know there is NP proof for quadratic residues, i.e. proof = the square root, but there is no NP proof for quadratic non-residues.

In Lecture 14, we gave interactive proofs for quadratic residuosity.

Indeed, we can also give an (honest-verifier perfect ZK) interactive for quadratic non-residuosity.

IP for QNR

The prover wants to convince the verifier that the $y$ is a quadratic non-residuosity.

The interactive protocol is as shown below.

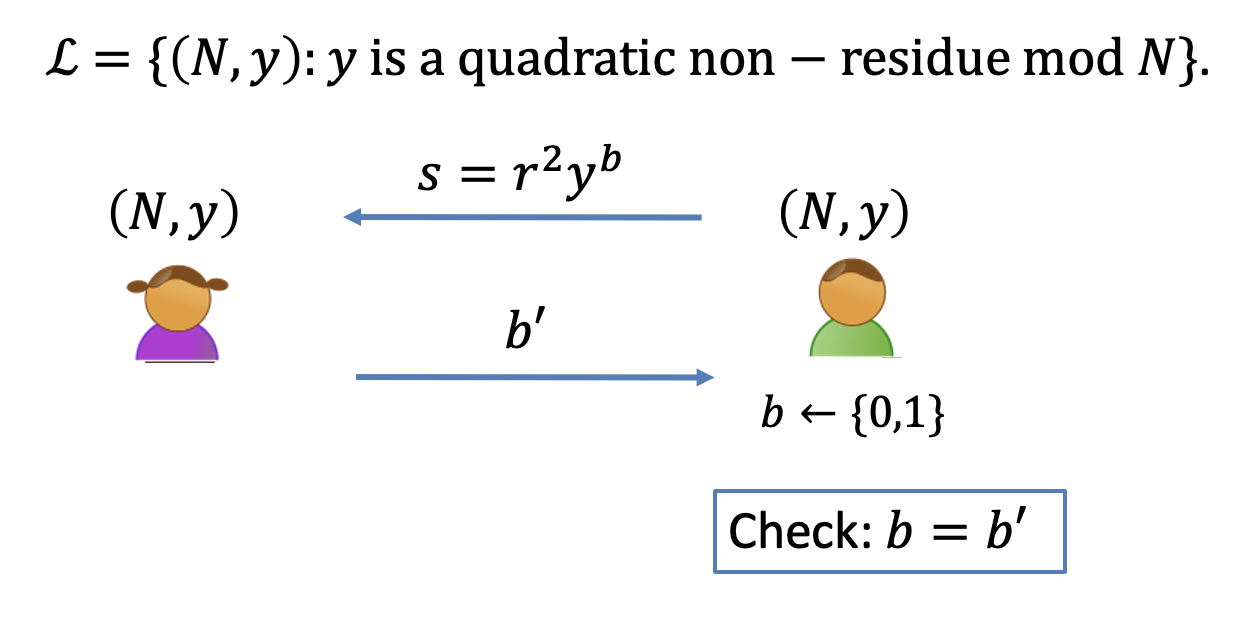
ZK Proof for Quadratic Non-residue:

• Verifier:
  1. pick a random $r$
  2. pick a random $b\gets{0,1}$
  3. send $s=r^2y^b$
• Prover:
  • guess $b’$
• Verifier Check: $b=b’$

The protocol is complete, sound and (honest-verifier perfect) zero-knowledge.

Completeness:

Recall that the completeness is the property of the protocol when the prover and the verifier are both honest.

If $y$ is non-square, the prover should be able to win.

The thing to point is that the prover knows $y$ is non-square, so maybe the she is unbounded or she knows the factorization of $N$ since there is no NP proof for QNR.

Hence, if $y$ is non-square, then the prover can tell $s$ is square or non-square to answer $b’$.

Soundness:

Recall that the soundness is the property of the protocol against malicious prover.

If $y$ is a square, then $r^2y^b$ is also a square.

Hence, the prover cannot cheat the verifier with probability better than $1/2$.

Then we can use sequential repetition or parallel repetition to reduce the soundness error.

Honest-Verifier Perfect Zero Knowledge:

Recall that the zero-knowledge is the property of the protocol against verifier.

The view of $V$ is $(r,b,b’)$, so the simulator can do exactly what $V$ dose.

The simulated view is $(r,b,b’=b)$ for a random $r$ and a random $b$.

---

Similarly, although there is no NP proof for graph non-isomorphism, there is an (honest-verifier perfect) interactive proof for graph non-isomorphism.

It turns out that IP can prove more stuff than NP.

Indeed, the IP = PSPACE >> NP.

PSPACE is the set of things that we can decide if we have polynomial memory to work with but potential exponential time.

It’s surprising that we can prove such a language, i.e. QNR, using interactive proofs.

IP = PSPACE >> NP[Lund-Fortnow-Karloof-Nisan’89, Shamir’90]

https://www.cs.princeton.edu/courses/archive/spring09/cos522/BabaiEmail.pdf

NIZK: The Common Random String Model

In last blog is introduced that we can achieve NIZK in the random oracle model.

In this section, we will introduce another way, the common random string model.

In this model, there is an angle coming up with random sequence of polynomial bits.

The angle could be the sunspots.

• Completeness: For every $G\in 3COL$, $V$ accepts $P$’s proof.

• Soundness: For every $G\notin3COL$ and any “proof” $\pi^\star$, $V(CRS,\pi^\star)$ accepts with probability $\le neg(n)$.

• Zero Knowledge: There is a PPT simulator such that for every $G\in 3COL$, $S$ simulates the view of the verifier $V$.

  $$
  S(G)\approx(CRS\gets D, \pi \gets P(G,\text{colors})
  $$

  • The view of verifier is $(CRS, \pi)$.
  • The simulator has to produce the simulated view without knowing the witness and the CRS. So the simulator has to fake potentially the common random and the proof.
  • If we sort of change the definition that the simulator gets a common random string and has to produce the view with a fixed CRS, then this definition is impossible to achieve.
    For the same reason that we prove the NIZK is impossible (Lecture 15), it dose not satisfy the soundness.

Similarly, the Common Reference String Model is that there is an angle coming up the random product of two primes, not a sequence of random bits. And it cannot be achieved by the sunspots.

Construct NIZK in the CRS Model

There are several constructions of NIZK in the CRS model.

1. Blum-Feldman-Micali’88 (quadratic residuosity)
2. Feige-Lapidot-Shamir’90 (factoring)
3. Groth-Ostrovsky-Sahai’06 (bilinear maps)
4. Canetti-Chen-Holmgren-Lombardi-Rothblum^2-Wichs’19 and Peikert-Shiehian’19 (learning with errors)

In this Lecture, we will introduce the first construction.

Blum-Feldman-Micali’88 (quadratic residuosity)

1. Review our number theory hammers & polish them.
2. Construct NIZK for a special NP language, namely quadratic non-residuosity.
3. Bootstrap to NIZK for 3SAT, an NP-complete language.

Quadratic Residuosity

More introduction is referred in Lecture 9

Let $N=pq$ be a product of two large primes.

Jacobi symbol ($Jac$) divides $\mathbb{Z}_N^*$ evenly unless $N$ is a perfect square.

• $Jac_{-1}$: non-squares
• $Jac_{+1}$: pseudo-squares

A surprising fact is Jacobi symbol $\left(\frac{x}{N}\right)=\left(\frac{x}{P}\right) \left(\frac{x}{Q}\right)$ is computable in poly. time without knowing $p$ and $q$. (using Law of Quadratic Reciprocity.[* 二次互反定理])

$x$ is square mod $N$ iff $x$ is square mod $p$ and square mod $q$, so we can even $Jac_{+1}$.

• $QR_N$: the set of squares mod $N$.
• $QNR_N$: the set of non-squares mod $N$. (but with Jacobi symbol $+1$)

Note: The following are new claims:

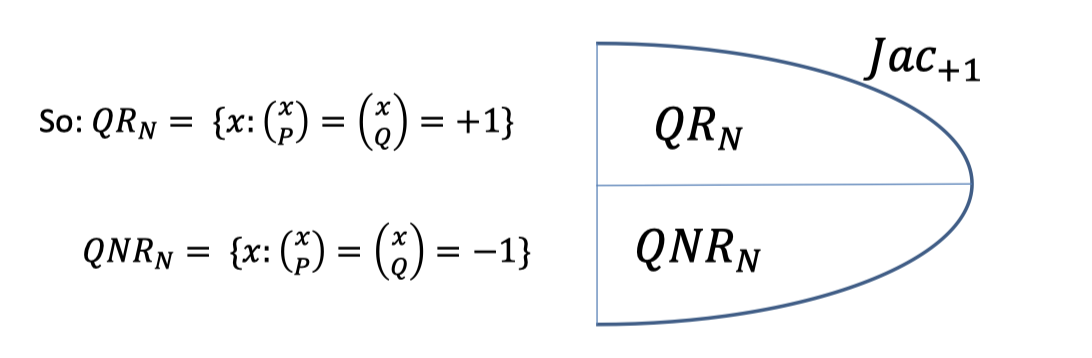
We call $N$ good if exactly half the elements of $\mathbb{Z}_N^*$ with Jacobi symbol $+1$ are squares.

Exactly half residues even iff $N=p^iq^j$ is odd, and $i,j\ge 1$, not both even.

If $N$ is good, there is an important property is if $y_1$ and $y_2$ are both in $QNR$, then their product $y_1y_2$ is in $QR$.

(This property will be used in the following NIZK for QNR)

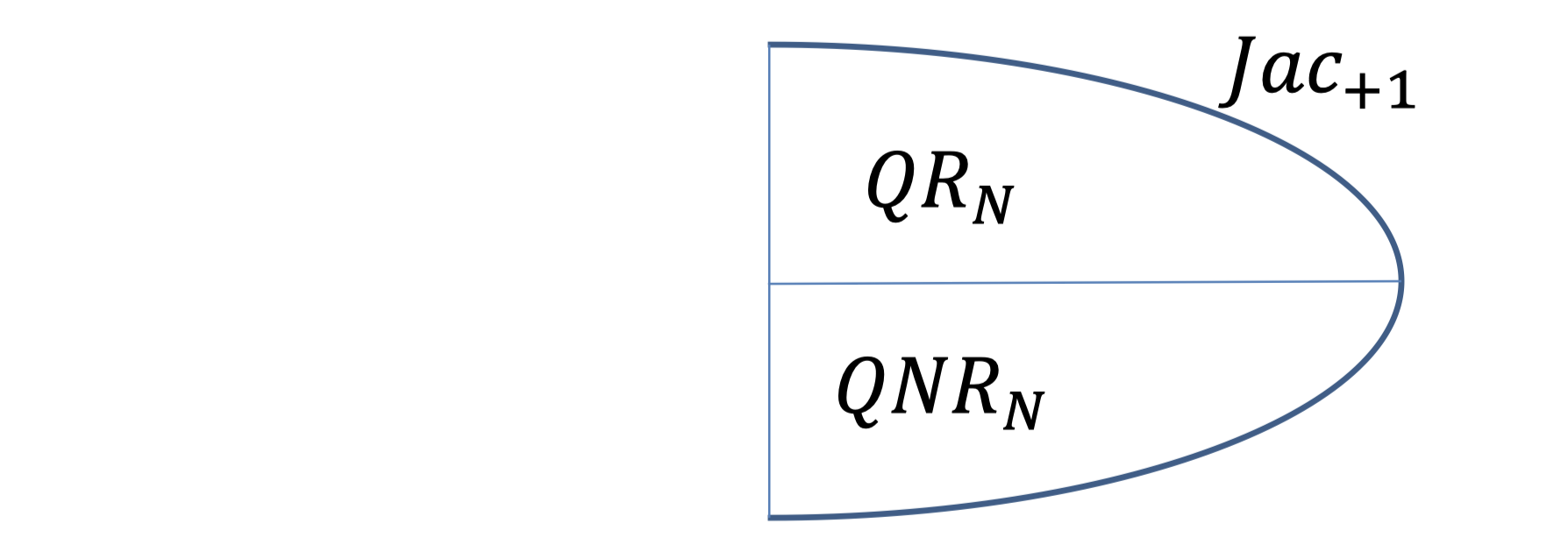
But if $N$ has three or more prime factors, the fraction of residues is smaller.

Analysis of $N=pqr$:

$x$ is square mod $N$ iff $x$ is square mod $p$, mod $q$ and mod $r$.

If $N=pqr$, the fraction of residues in $Jac_{+1}$ is $1/4$ as shown in table below.

Jac	(x/p)	(x/q)	(x/r)
1	1	1	1
1	1	-1	-1
1	-1	1	-1
1	-1	-1	1
-1	1	1	-1
-1	1	-1	1
-1	1	1	-1
-1	-1	-1	-1

Besides, the property, “ if $y_1$ and $y_2$ are both in $QNR$, then their product $y_1y_2$ is in $QR$”, is no longer satisfied.

---

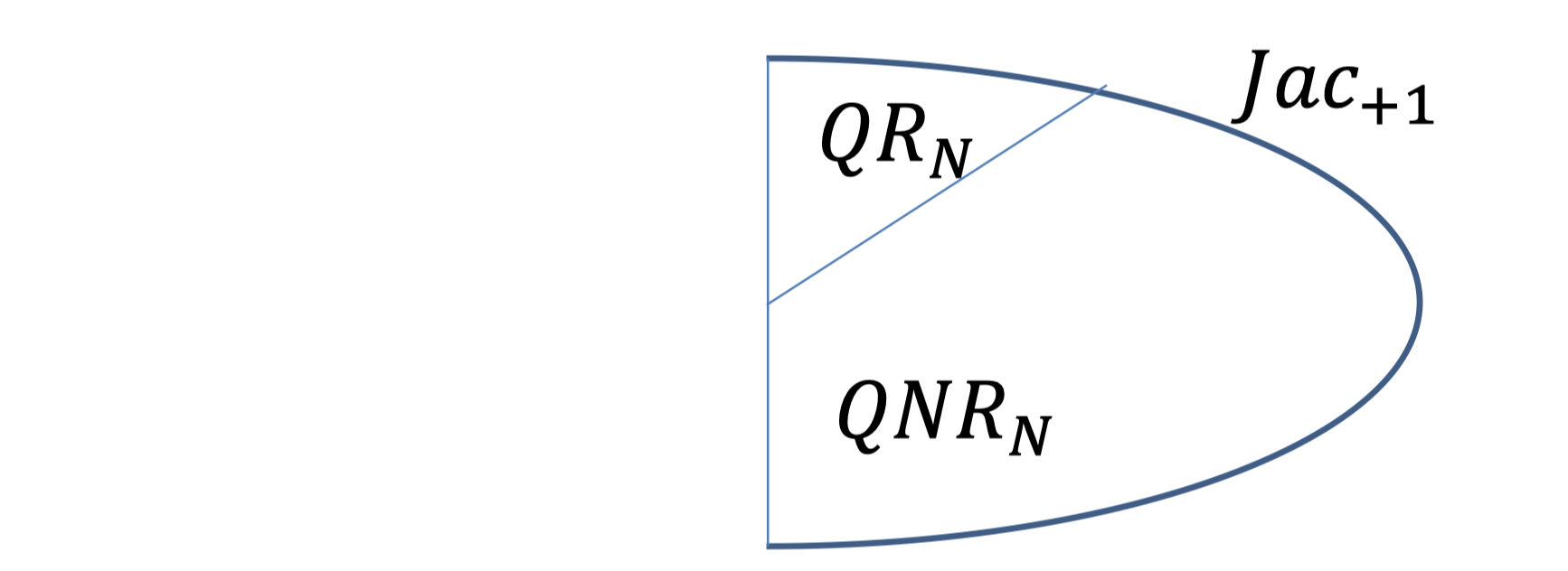
Quadratic Residuosity Assumption (QRA):

Let $N=pq$ be a product of two large primes.

No PPT algorithm can distinguish between a random element of $QR_N$ from a random element of $QNR_N$ given only $N$.

NIZK for QNR

Define the NP language GOOD with instance $(N,y)$ where

• $N$ is good; and
• $y\in QNR_N$ (that is, $y$ has Jacobi symbol $+1$ but is not a square mod $N$)

The non-interactive protocol is as follows.

The prover wants to convince the verifier that $(N,y)$ is good.

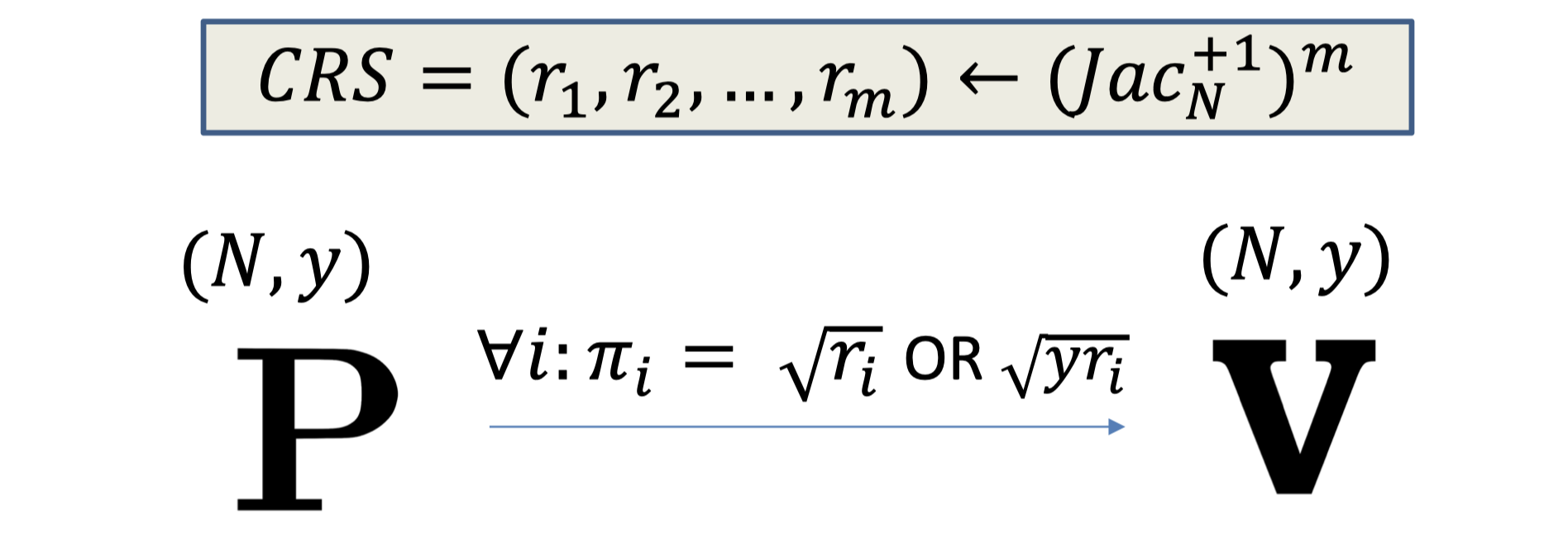
NIZK for QNR:

• $CRS = (r_1,r_2,\dots,r_m)$ where each $r_i$ is sampled from $Jac_N^{+1}$.
• The proof is $\forall i: \sqrt{r_i}$ or $\sqrt{yr_i}$
• The verifier check
  • $N$ is odd
  • $N$ is not a prime power
  • $N$ is not a perfect square
  • (Fact: If the preceding three passes, then at most half of $Jac_N^{+1}$ are squares.)
  • I received either a mod-$N$ square root of $r_i$ or $yr_i$.

Completeness:

If $N$ is good and $y\in QNR_N$, the prover can compute either $\sqrt{r_i}$ or $\sqrt{yr_i}$.

• The prover has a knowledge that $y$ is non-residuosity. So, maybe she is unbounded or knows the factorization of $N$.
• If $r_i\in QR_N$: the prover can compute $\sqrt{r_i}$.
• If $r_i\in QNR_N$: $yr_i$ is square by the property above so the prover can compute $\sqrt{yr_i}$.

Soundness:

What if $N$ has more than $2$ prime factors ?

No matter what $y$ is, for half the $r_i$ , both $r_i$ and $yr_i$ are not quadratic residues.

So the prover cannot compute either $\sqrt{r_i}$ or $\sqrt{yr_i}$ for half the $r_i$.

• Suppose $N=pqr$
• The fraction of quadratic residues in $Jac_{+1}$ is $1/4$.
• Besides, the property, “ if $y_1$ and $y_2$ are both in $QNR$, then their product $y_1y_2$ is in $QR$”, is no longer satisfied.

The thing to notice is that the proof only proves $N$ is good, not $N=pq$.

Perfect Zero Knowledge Simulator S:

First pick the proof $\pi_i$ to be random in $\mathbb{Z}_N^*$.

Then reverse-engineer the CRS, letting $r_i=\pi_i^2$ or $r_i=\pi_i^2/y$ randomly.

The distribution of simulated view is identical to the real view.

Warning:We define $CRS = (r_1,r_2,\dots,r_m)$ where each $r_i$ is sampled from $Jac_N^{+1}$.

The CRS depends on the instance $N$. Not good.
An alternative solution is

1. Let CRS be random numbers.
2. Interpret them as elements of $\mathbb{Z}_N^*$ and both the prover and the verifier filter out $Jac_N^{-1}$.

NIZK for 3SAT

From Wiki:

SAT:
In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula.
SAT is the first problem that was proven to be NP-complete.
This means that all problems in the complexity class NP, which includes a wide range of natural decision and optimization problems, are at most as difficult to solve as SAT.

3SAT:
Like the satisfiability problem for arbitrary formulas, determining the satisfiability of a formula in conjunctive normal form where each clause is limited to at most three literals is NP-complete also; this problem is called 3-SAT, 3CNFSAT, or 3-satisfiability.

Literal:
In mathematical logic, a literal is an atomic formula (atom) or its negation.

• Boolean Variables: $x_i$ can be either true(1) or false(0).
• A Literal is either $x_i$ or $\overline{x_i}$
• A Clause is a disjunction of literals.
  • A Clause is true if any one of the literals is true.
  • E.g. $x_1\vee x_2\vee \overline{x_5}$ is true as long as $(x_1,x_2,x_5)\ne(0,0,1)$
• A 3-SAT formula is a conjunction of many 3-clauses.
  • A 3-SAT formula $\Psi$ is satisfiable if there is an assignment of values to the variables $x_i$ that makes all its clauses true.
  • $\Psi=\left(x_{1} \vee x_{2} \vee \overline{x_{5}}\right) \wedge\left(x_{1} \vee x_{3} \vee x_{4}\right)\wedge\left(\overline{x_{2}} \vee x_{3} \vee \overline{x_{5}}\right)$

Cook-Levin Theorem:

It is NP-complete to decide whether a 3-SAT formula $\Psi$ is satisfiable.

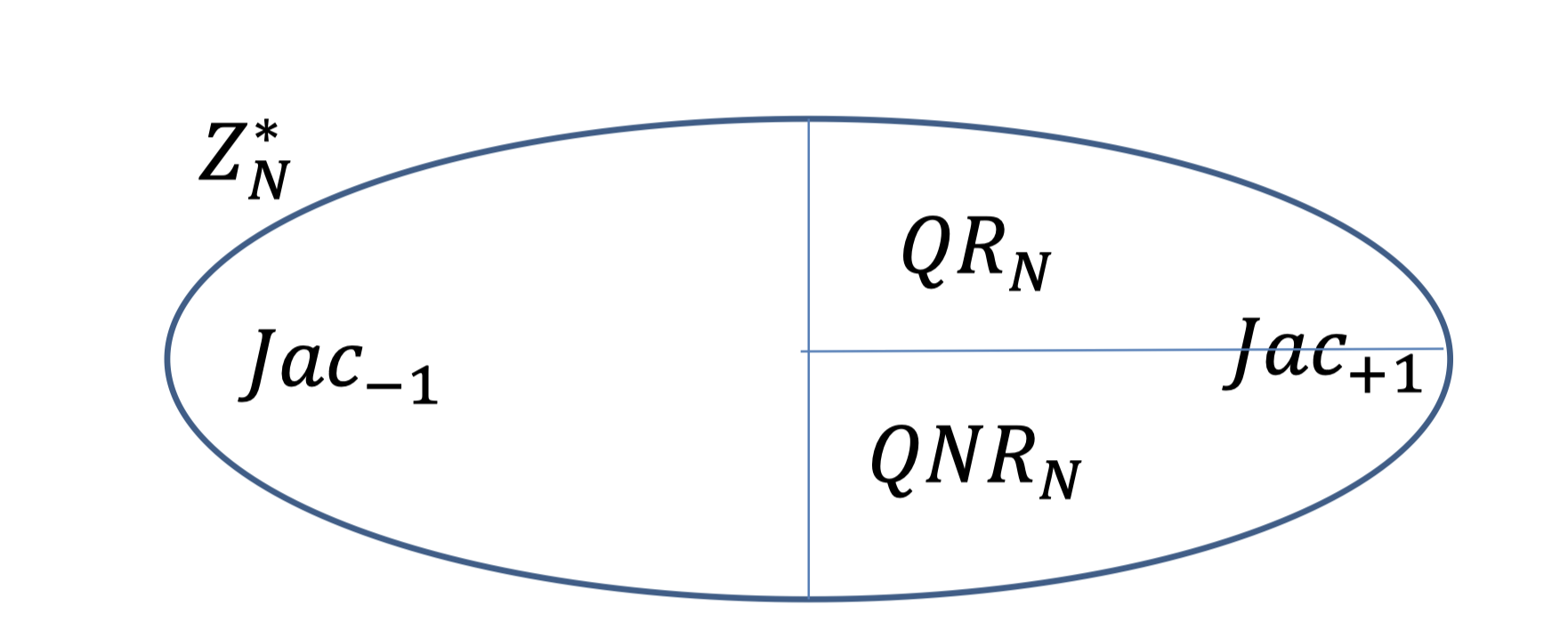
Recall NIZK for QNR.

We saw a way to show that a pair $(N,y)$ is GOOD. That is:

• the following is the picture of $\mathbb{Z}_N^*$ and
• for every $r\in Jac_{+1}$, either $r$ or $ry$ is a quadratic residue.

The prover wants to convince the verifier that $\Psi$ is satisfiable.

The input $\Psi=\left(x_{1} \vee x_{2} \vee \overline{x_{5}}\right) \wedge\left(x_{1} \vee x_{3} \vee x_{4}\right)\wedge\left(\overline{x_{2}} \vee x_{3} \vee \overline{x_{5}}\right)…$ with $n$ variables and $m$ clauses.

The non-interactive protocol is as follows.

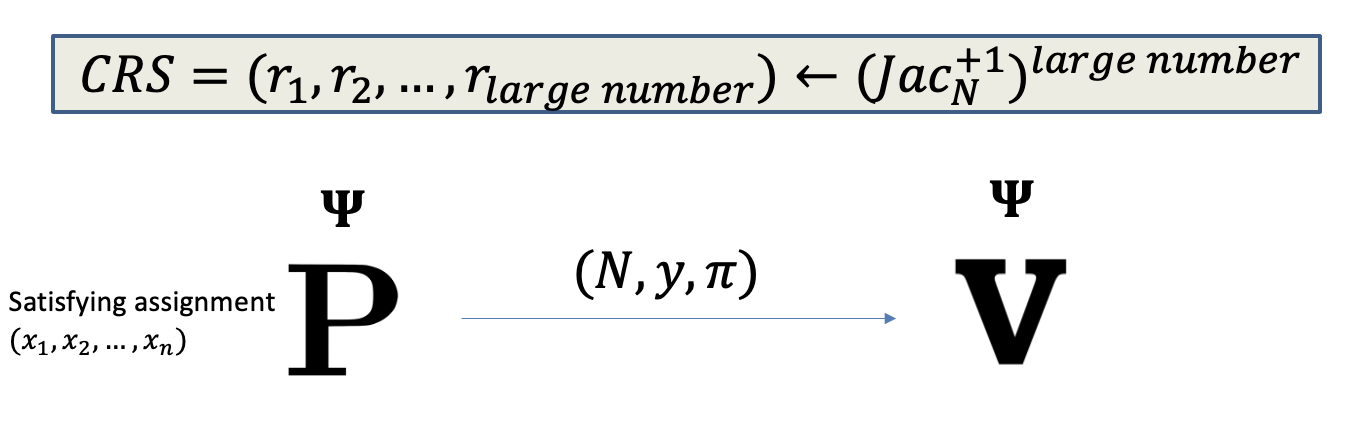
NIZK for 3SAT:

• $CRS=(r_1,r_2,…)$ where each $r_i$ is sampled from $Jac_N^{+1}$.
  Note: Similarly, we can Let CRS be random numbers and interpret them as elements of $\mathbb{Z}_N^*$, and both the prover and the verifier filter out $Jac_N^{-1}$.

1. Prover picks an $(N,y)$ and proves that it is GOOD. (as defined above)
2. Prover encodes the satisfying assignment and sends the encode variables $(y_1,\dots,y_n)$ to $V$.
   We should hide the values to achieve zero knowledge so the encoding is indeed a commitment.
   1. $y_i\gets QR_N$ if $x_i$ is false (encryption of $0$ is a residue)
   2. $y_i \gets QNR_N$ if $x_i$ is true (encryption of $1$ a non-residue)
   3. For the literal $x_i$,
      1. $Enc(x_i)=y_i$
      2. $Enc(\overline{x_i})=yy_i$
   4. exactly one of the $Enc(x_i)$ or $Enc(\overline{x_i})$ is a non-residue.
      1. A residue is indeed the encryption of 0(false)
      2. A non-residue is indeed the encryption of 1(true)
3. Prove that (encoded) assignment satisfies each clause.
   1. For each clause, say $x_1\vee x_2\vee \overline{x_5}$, we WANT to SHOW: $x_1$ OR $x_2$ OR $\overline{x_5}$ is true.
   2. Let $(a_1=y_1,b_1=y_2,c_1=yy_5)$ denote the encoded variables.
   3. So, each of them is either $y_i$ (if the literal is a var) or $yy_i$ (if the literal is a negated var).
   4. Now, we WANT to SHOW: $a_1$ OR $b_1$ OR $c_1$ is a non-residue.

A terrible way is to prove $a_1$ is non-residue or $b_1$ is non-residue.

If the prover convinces the verifier that $a_1$ is non-residue, $P$ indeed tells $V$ that $x_1$ is true(1).

Hence, we want to prove one of them is a non-residue without telling the verifier that which one is non-residue.

WANT to SHOW: $a_1$ OR $b_1$ OR $c_1$ is a non-residue

• Equivalently, the signature of $(a_1,b_1,c_1)$ is NOT (QR, QR, QR).

• A clever idea is to generate seven additional triples.

  
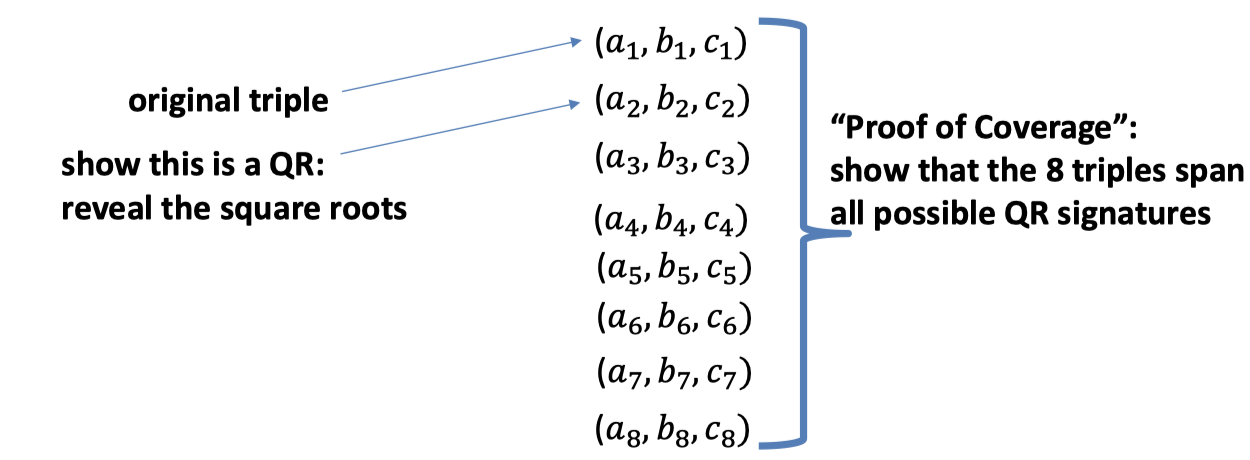
  • The original triple is $(a_1,b_1,c_1)$.
  • This 8 triples span all possible QR signatures.
  • There is one triple is (QR, QR, QR), e.g. the second triple, and reveal the square roots of this triple.
  • Then we can prove the origin triple is NOT (QR, QR, QR).

• Proof consists of two parts

  • Proof of Coverage : show that the 8 triples span all possible QR signatures.
    • For each of poly. many triples $(r,s,t)$ from CRS, show one of the 8 triples has the same signature.
    • That is, there is a triple $(a_i,b_i,c_i)$ s.t. $(ra_i,sb_i,tc_i)$ is (QR, QR, QR)
  • Show one triple (except the original triple) is (QR, QR, QR) and reveal the square roots.

Hence, the full proof is as follows.

1. Prover picks an $(N,y)$ and proves that it is GOOD.

2. Prover encodes the satisfying assignment and sends the encode variables $(y_1,\dots,y_n)$ to $V$.

3. Prove that (encoded) assignments satisfy each clause.

   For each clause, construct the proof $\rho$ = (7 additional triples, square root of the second triples, proof of coverage).

Completeness and Soundness can be inherited from NIZK for QNR.

Computational Zero Knowledge Simulator S:

Simulator picks $(N,y)$ where $y$ is a quadratic residue.

The following proof is my own deduction since the proof is omitted in the lecture.
Corrections and advice are welcome.

• Simulated view of $(N,y, \pi)$
  1. Pick the proof $\pi_i$ to be random in $\mathbb{Z}_N^*$.
  2. Reverse-engineer the CRS, letting $r_i=\pi_i^2$ or $r_i=\pi_i^2/y$ randomly.
  • Then $r_i=\pi_i^2$ and $r_i=\pi_i^2/y$ are both residues.
  • The distribution of simulated view is computationally indistinguishable to the real view.
• Simulated view of encoded assignments $(y_1,\dots, y_n)$
  • $y_i \gets QNR_N$ whether $x_i$ is true or false (encryptions are both non-residues)
    • $Enc(x_i)=y_i$ (encryption of $1$ is a non-residue)
    • $Enc(\overline{x_i})=yy_i$ (encryption of $0$ is a non-residue)
  • Encoding of ALL literals can be set to true.

Proofs vs. Argument

Before proceeding to the evolution of proofs, let’s discuss the difference between proofs and arguments.

The main difference is the definition in soundness.

In Lecture 14, we gave the definition of soundness in Proofs that nobody can convince you a false statement. We mentioned that the soundness holds agains unbounded provers.

Arguments is where the soundness holds against only computational bounded provers.

It’s actually weakening the notion of proof.

Why do we still introduce the the argument ?

1. It allows us to get perfect zero knowledge for all of NP.
   Recall perfect ZK proofs do not exist for NP-complete languages, unless the polynomial hierarchy collapses. It turns out that if we weaken the notion of proofs, then we can construct the perfect zero knowledge systems.
2. It allows us to get very short proof = succinct arguments or SNARGs.
   SNARKs : succinct arguments of knowledge.

The Evolution of Proofs

Proofs have been evolving over generations.

• CLASSIC Proofs (Complexity class: NP) Prover writes down a string (proof); And Verifier checks.
• INTERACTIVE Proofs (Complexity class: IP = PSPACE >> NP) Prover and verifier talk back and forth. In last blog, we introduced the zk proof for quadratic non-residue.
• PROBABILISTICALLY CHECKABLE Proofs (Complexity class: NEXP >> PSPACE) Non-interactive, but verifier only looks at 3 bits of proof.
• MULTIPROVER interactive proofs
• Proofs in the wild: ZCash