「Cryptography-MIT6875」: Lecture 8

In this series, I will learn MIT 6.875, Foundations of Cryptography, lectured by Vinod Vaikuntanathan.
Any corrections and advice are welcome. ^ - ^

Topics Covered:

• Public-key Encryption and Key exchange.
• Definitions: IND-Security (IND-CPA)
• Trapdoor permutations.

Key Agreement Problem

There is a remaining problem in secret-key encryption (or symmetric encryption), the Key Agreement Problem.

How did Alice and Bob get the same $sk$ to begin with ?

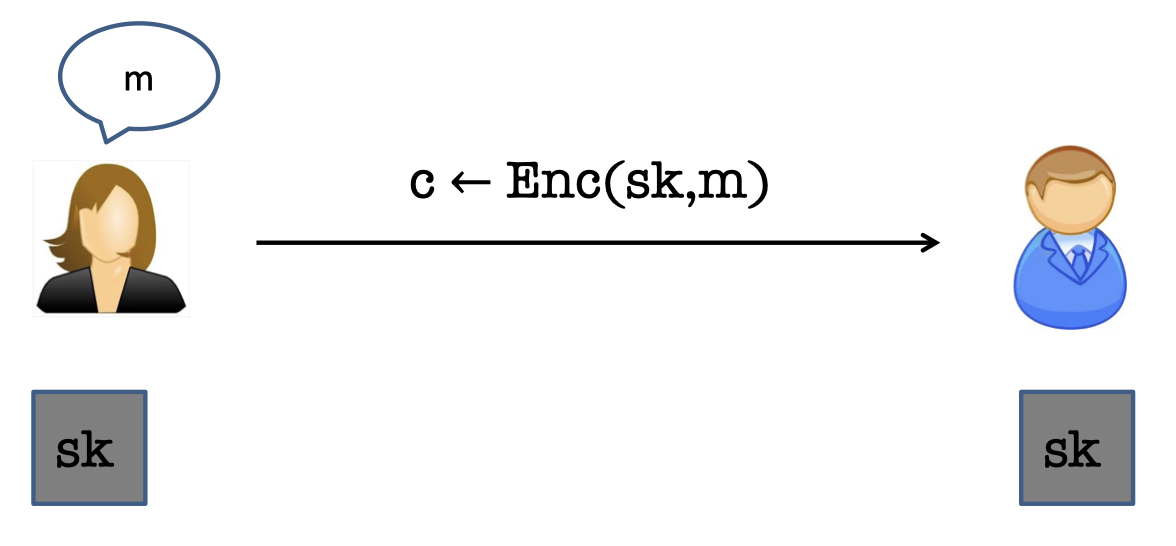
Can Alice and Bob, who never previously met, exchange messages securely ?

Merkle’s [1974]

The Merkle’s idea is based on one-way function.

Assume that $H:[n^2]\rightarrow [n^2]$ is an injective OWF. (or one-to-one).

Injective Function:

In mathematics, an injective function (also known as injection, or one-to-one function) is a function $f$ that maps distinct elements to distinct elements.

• That is, $f(x_1) = f(x_2)$ implies $x_1 = x_2$.

• Equivalently, $x_1\ne x_2$ implies $f(x_1) \ne f(x_2)$ in the equivalent contrapositive statement.

1. Alice picks $n$ random numbers $x_1,\dots,x_n$
2. Bob picks $n$ random numbers $y_1,\dots, y_n$

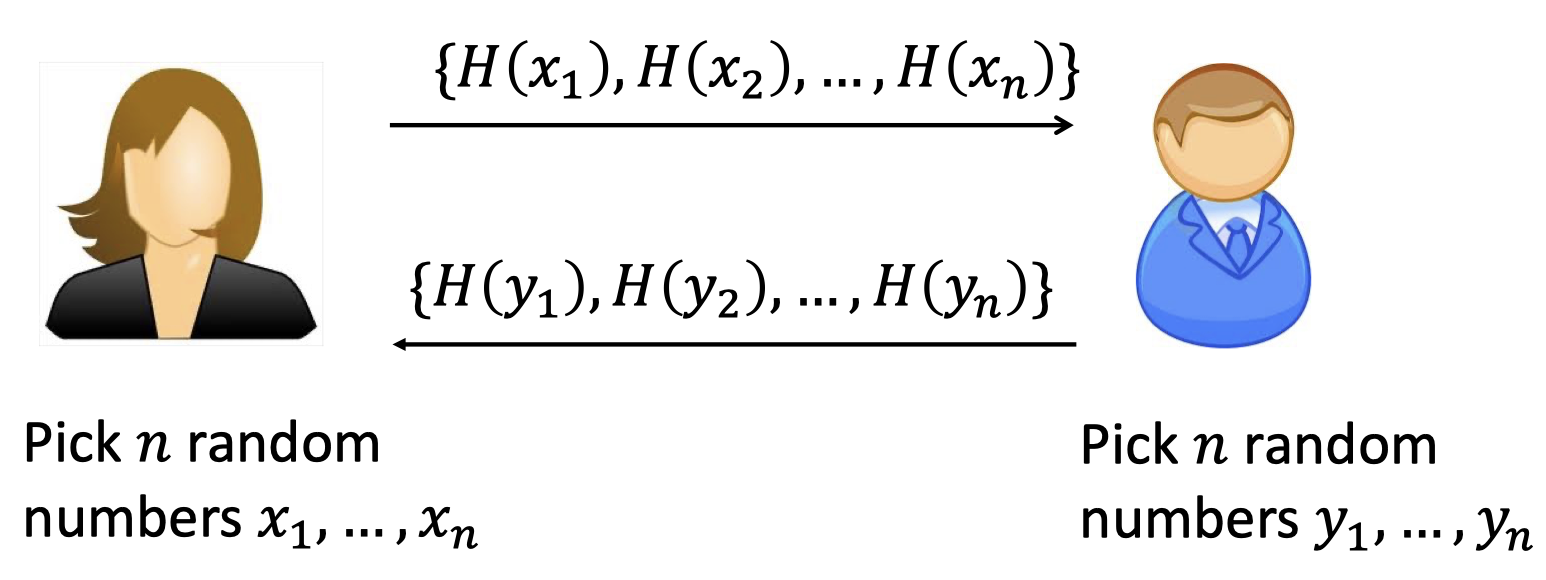
3. There is a common number since birthday paradox.
   That says $x_i=y_j$ with high probability.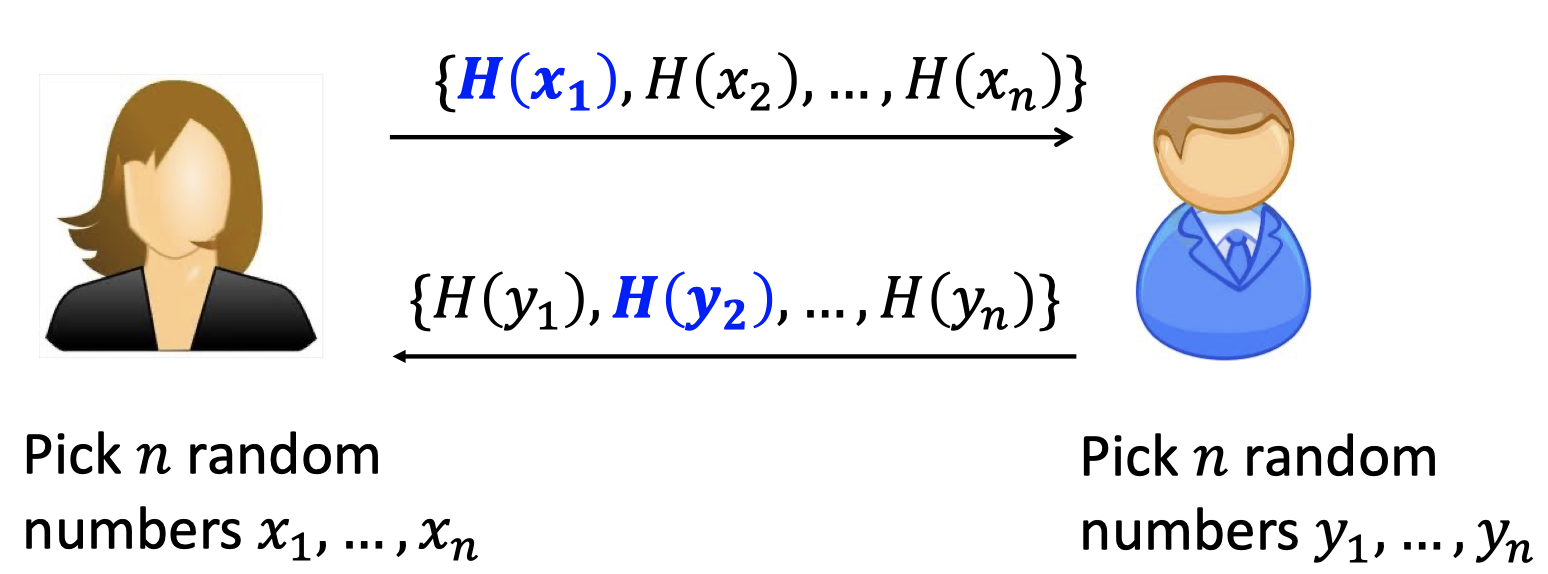

   

4. Alice and Bob can detect it in time $\mathcal{O}(n)$, and they set it as their shared key.

---

How long dose it take Eve, the adversary to compute the shared key ?

She knows $i$ and $j$ since she can see the ciphertexts in the channel, but she needs to inver the OWF.

Assuming the OWF is very strong, that is $\Omega(n^2)$.

But the Merkle’s only protects against quadratic-time Eves although it’s still an excellent idea.

Fascinating History

The Public-key Encryption has a fascinating history.

• Merkle (1974):
  “Secure Communications Over Insecure Channels.”
  • Only protects against quadratic-time adversary.
• Diffie & Hellman (1976):
  “New Direction in Cryptography”
  • Turing Award 2015.
  • Marked the birth of public-key cryptography.
  • Invented the Diffie-Hellman key exchange.
    (conjectured to be secure against all poly-time attackers unlike Merkle)
  • Used to this day (e.g., TLS 1.3) albeit with different groups than what DH had in mind.
• Rivest, Shamir & Adleman (1987):
  “A Method for Obtaining Digital Signatures and Public-Key Cryptosystems”
  • Turing Award 2002.
  • Invented the RSA trapdoor permutation, public-key encryption and digital signatures.
  • RSA Signatures used to this day (e.g., TLS 1.3) in essentially the original form it was invented.
• Goldwasser & Micali (1982):
  “Probabilistic Encryption”
  • Turning Award 2012.
  • Defined what is now the gold-standard of security of public-key encryption
    (two equivalent definitions: indistinguishability and semantic security)
  • GM-encryption: based on the difficulty of the quadratic residuosity problem, the first homomorphic encryption.

Public-Key Encryption

It’s also called Asymmetric Encryption.

The goal is :

• Anyone can encrypt to Bob
• Bob, and only Bob can decrypt.

Public-key Encryption Scheme

The public encryption scheme works as follows:

1. Bob generate a pair of keys, a public key $pk$, and a private (or secret) key $sk$.
2. Bob “publishes” $pk$ and keeps $sk$ to himself.
3. Alice encrypts $m$ to Bob using $pk$.
4. Bob decrypts using $sk$.

Hence, there are a triple of PPT algorithms $(Gen, Enc, Dec)$ s.t.

• $Gen(1^n)\rightarrow (pk,sk)$:

PPT Key generation algorithm generates a public-private key pair.

• $Enc(pk,m)\rightarrow c$:

Encryption algorithm uses the public key to encrypt message $m$.

• $Dec(sk,c)\rightarrow m$:

Decryption algorithm uses the private key to decrypt ciphertext $c$.

Correctness:
For all $pk,sk,m$: $Dec(sk,Enc(pk,m))=m$.

Define the Adversary

But how to define security ?

What dose Eve know ?

• Eve knows Bob’s public key $pk$
• Eve sees polynomially many ciphertexts $c_1,c_2,\dots$ of messages $m_1,m_2,\dots$

So the challenge is that Eve should not get any partial information about the set of messages.

IND-Security (IND-CPA)

We define the Indistinguishability Security, or Indistinguishability-CPA.

CPA is the abbreviation of Chosen Plaintext Attack.
That is, the adversary has the power of obtaining the encryption of arbitrary message of his choice.

We give the definition by a game, which is actually the same as the Turning Test.

Many Message Security

Define the Game:

1. The Challenger generates a pair of key $(pk, sk)$ and publishes the $pk$.
2. Eve sends two vectors of message, $\vec{m_0}$ and $\vec{m_1}$s.t. $|m_0^i|=|m_1^i|$ for all $i$.
   (A important restrict is $|m_0^i|=|m_1^i|$ for all $i$, or there is a length attack.)
3. The challenger samples $b$ from ${0,1}$ and encrypts all the messages in vector $\vec{m_b}$ using $pk$.
   And send the sequence of the ciphertext to Eve.
4. Eve guesses which vector of message is encrypted and output $b’$.
5. Eve wins if $b’=b$.

IND-security Definition (Many-message) (unachievable):

The encryption scheme is IND-secure if no PPT EVE can win in this game with probability better than $1/2 + \text{negl}(n)$.

---

Or written in more traditional (and cumbersome) notation as below.
For all PPT pair of algorithms $(M,A)$, there is a negligible function $\mu$ s.t.:[cumbersome:笨重的；不方便的]
$$
\operatorname{Pr}\left[\begin{array}{c} (pk,sk)\gets Gen(1^n); \ (\vec {m_o},\vec{m_1},state)\gets M(pk) s.t. |m_0^i|=|m_1^i|; \ \vec{c}\gets Enc(pk,\vec{m_b}) :A(state,\vec{c})=b\end{array}\right] \le \frac{1}{2} +\mu(n)
$$

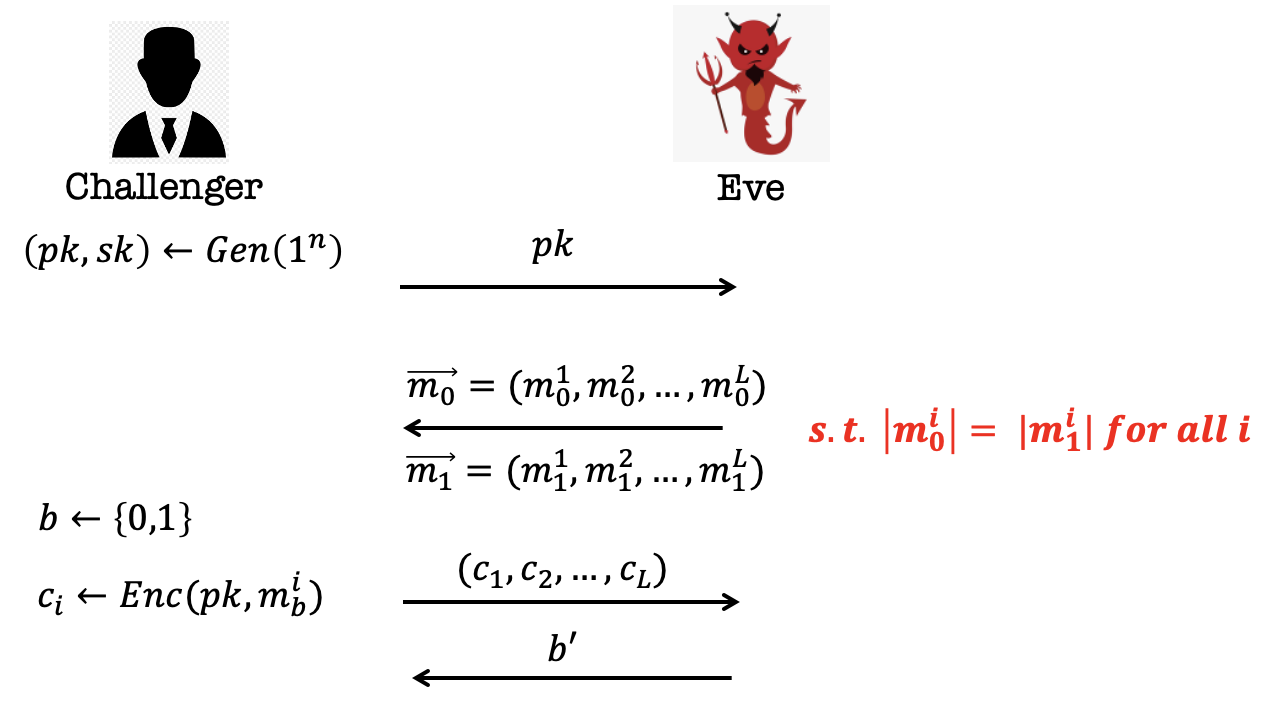
Yet the definition is unachievable. There is a simple way to win the game.

You can construct two vector of message in which one is composed of the same message and the other is composed of the different message.

Hence, it has to be randomized.

---

In [Lecture 1], we gave two security definitions in Symmetric-key Encryption, Shannon’s Perfect Secrecy and Perfect Indistinguishability.

Similarly, in Asymmetric-key Encryption, there is an alternative definition, Semantic Security, corresponding to the Indistinguishability Security.

The Semantic Security is the computational analog of Shannon’s Shannon’s Perfect Secrecy, and it turns to be equivalent to Indistinguishability Security.

i.e. Semantic Security = IND-Security. But the proof is more complex.

We will stick to IND-security as it’s easy to work with.

One Message Security

It’s cumbersome to define with many messages.

Actually, the definition can be simplified to One Message Security.

The only difference is that Eve can only see one ciphertext rather than a sequence of ciphertexts in the game.

Define the Game:

1. The Challenger generates a pair of key $(pk, sk)$ and publishes the $pk$.
2. Eve send two single messages, $m_0$ and $m_1$s.t. $|m_0|=|m_1|$.
3. The challenger sample $b$ from ${0,1}$ and encrypt the message $m_b$ using $pk$.
   And send the ciphertext to Eve.
4. Eve guesses which message is encrypted and output $b’$.
5. Eve wins if $b’=b$.

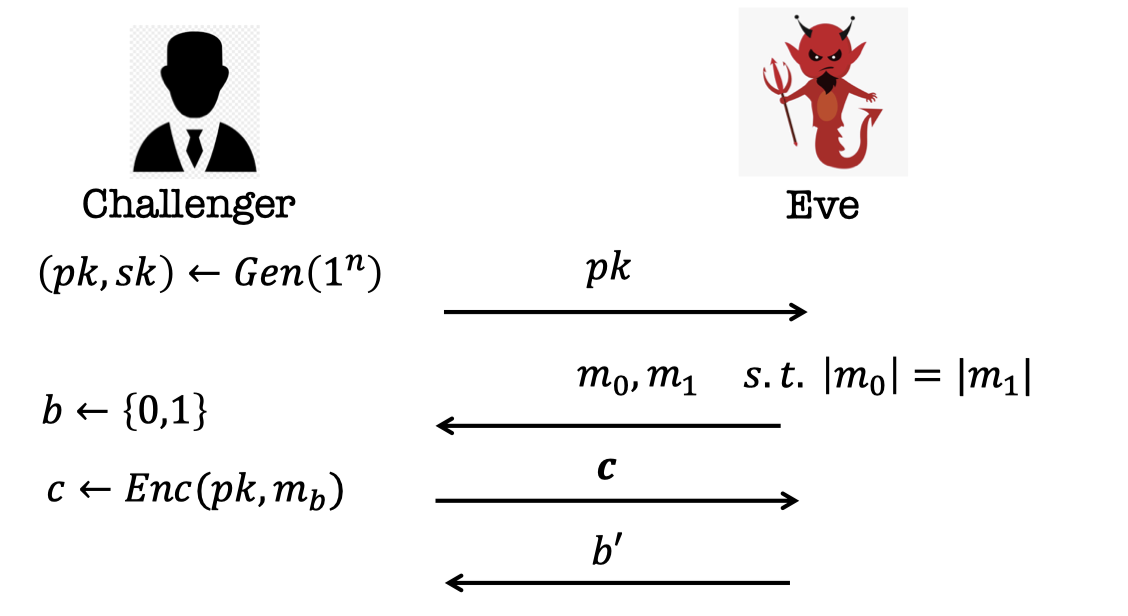
One-message IND-security Definition (unachievable):

The encryption scheme is single-message-IND-secure if no PPT EVE can win in this game with probability better than $1/2 + \text{negl}(n)$.

Similarly, it’s unachievable.

In public-key encryption, Eve knows the $pk$ as well. So she has the power of generating any ciphertext for arbitrary message of her choice, which is the meaning of CPA.

When she gets the ciphertext from the Challenger, she can easily distinguish it.

Because she can generate the ciphertexts of $m_0$ and $m_1$ using $pk$.

Hence, only in public-key encryption, the many message security implies one message security.

It dose not work with secret-key encryption.

Theorem:

A public-key encryption scheme is IND-secure iff it is single-message IND-secure.

The proof is the simple use of Hybrid Argument.

---

We’ll show four constructions in following blogs.

1. Trapdoor Permutations (RSA)
2. Quadratic Residuosity/Goldwasser-Micali
3. Diffie-Hellman/El Gamal
4. Learning with Errors/Regev

In this blog, we introduce the Trapdoor Permutations.

Trapdoor Functions

We know one-way function (family) is easy to compute but hard to invert.

But Trapdoor One-way Function (family) is easy to invert given a trapdoor.

Besides, it’s Trapdoor One-way Permutation when domain = range.

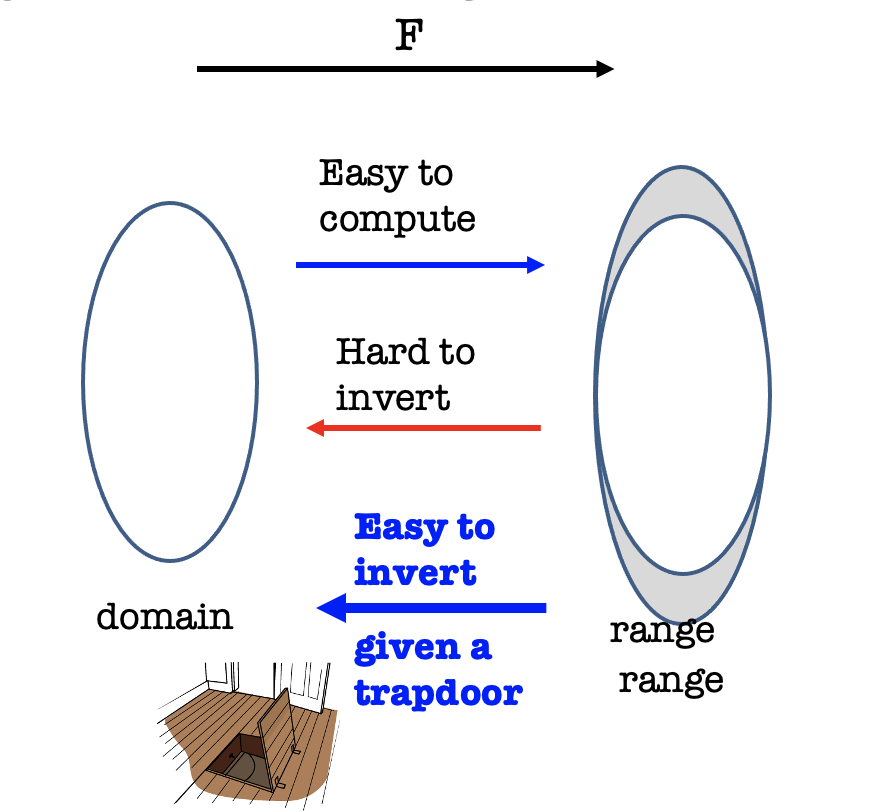
Definition

Definition:

A function (family) $\mathcal{F=\{F_n\}}_{n\in\mathbb{N}}$ where each $\mathcal{F_n}$ is itself a collection of functions $\mathcal{F_n}=\{F_i:\{0,1\}^n\rightarrow \{0,1\}^{m(n)}\}_{i\in I_n}$ is a trapdoor one-way function family if

• Easy to sample function index with a trapdoor.
  There is a PPT algorithm $Gen(1^n)$ that outputs a function index $i\in I_n$ together with a trapdoor $t_i$.

• Easy to compute $F_i(x)$ given $i$ and $x$.

• Easy to compute an inverse of $F_i(x)$ given $t_i$.

• It is one-way.
  That is, for every p.p.t. $A$, there is a negligible function $\mu$ s.t.

  $$ \operatorname{Pr}\left[\begin{array}{c}(i, t) \leftarrow \operatorname{Gen}\left(1^{n}\right) ; x \leftarrow\{0,1\}^{n} ; y=F_{i}(x) ; \\ A\left(1^{n}, i, y\right)=x^{\prime}: y=F_{i}\left(x^{\prime}\right)\end{array}\right] \leq \mu(n) $$

Public-key Encryption Construction

We can construct IND-Secure Public-key Encryption from Trapdoor Permutations.

There are three p.p.t. algorithms.

Not IND-Secure (without randomization):

• $Gen(1^n)$: Sample function index $i$ with a trapdoor $t_i$.
  The public key is $i$ and the private key is $t_i$.
• $Enc(pk=i,m)$: Output $c=F_i(m)$ as the ciphertext.
• $Dec(sk=t_i,c)$: Output $F_i^{-1}(c)$ computed using the private key $t_i$.

However, it is NOT IND-secure since it could reveal partial information about $m$.

IND-Security is unachievable without randomization as we mentioned before in the IND-security definition.

In last lecture [(Lecture 7)], we introduced GL Theorem that every one-way function has a hardcore bit . Besides, we showed one-way permutation implies PRG.

(In fact, one-way function implies PRG as well.)

Hence, we can construct a PRG from the trapdoor permutation, which is pseudorandom.

IND-Secure (with PRG from trapdoor permutations):

• $Gen(1^n)$: Sample function index $i$ with a trapdoor $t_i$.
  The public key is $i$ and the private key is $t_i$.
• $Enc(pk=i,m)$ where $m$ is a bit.
  • Pick a random $r$.
  • Output $c=(F_i(r),HCB(r)\oplus m)$ as the ciphertext.
• $Dec(sk=t_i,c)$:
  • Recover $r$ using the private key $t_i$.
  • Decrypt $m$ using $HCB(r)$.

Notation: If the message is $k$-bit, it has to run the encryption $k$ times, each of which is encrypting one bit.

This public-key encryption is IND-secure.

It looks familiar with the stateless secret-key encryption with PRF.

“Stateless Secret-key Encryption with PRF:” in Lecture 4

• $Gen(1^n)$: Generate a random $n$-bit key $k$ that defines $f_k:\{0,1\}^l\rightarrow \{0,1\}^m$.
  The domain size of $f_k$, $2^l$, had better be super-polynomially large in $n$.

• $Enc(k,m)$: Pick a random $x$ and let the ciphertext $c$ be the pair $(x,y=f_k(x)\oplus m)$.
  It’s a polynomial time to evaluate $f_k(x)$ since $f_k$ are random accessible.

• $Dec(k,c=(x,y))$: Output $f_k(x)\oplus y$.

The proof is by hybrid argument.

(It is also familiar with the proof of secret-key encryption using PRF in Lecture 4.)

Proof:

The following proof is my own deduction since the proof is omitted in the lecture.
Corrections and advice are welcome.

• From the (One-message) IND-Security definition,
  we want to prove the following two ciphertexts are indistinguishable.
  • ciphertext of $m_0$: $c=(F_i(r),HCB(r)\oplus m_0)$
  • ciphertext of $m_1$: $c=(F_i(r),HCB(r)\oplus m_1)$
• We define a sequence of hybrid distributions by changing the ciphertext a little bit.
  Consider the ciphertext as the distribution.
  Direction: Hybrid 0 → Hybrid 3 ← Hybrid6
  • Hybrid 0: $D$ gets the ciphertext of $m_0$
    $c=(F_i(r),HCB(r)\oplus m_0)$
  • Hybrid 1: replace with the hardcore bit
    $c=(F_i(r),HCB(r))$
  • Hybrid 2: replace with a random bit $r_b$
    $c=(F_i(r),r_b)$
  • Hybrid 3: replace with a random $r_x$ s.t. $|r_x|=|F_i(r)|$
    $c=(r_x,r_b)$
  • Hybrid 4: replace with a random bit $r_b$ (like Hybrid 2)
    $c=(F_i(r),r_b)$
  • Hybrid 5: replace with the hardcore bit (like Hybrid 1)
    $c=(F_i(r),HCB(r))$
  • Hybrid 6: $D$ gets the ciphertext of $m_1$
    $c=(F_i(r),HCB(r)\oplus m_1)$
• The thing we want to prove is that Hybrid 0 and Hybrid 6 are indistinguishable.
• Prove Hybrid 0 = Hybrid 1 (and Hybrid 6 = Hybrid 5) by birthday paradox.
  The probability of $D$ distinguishing from Hybrid 0 and Hybrid 1 is up to the collision probability of $r$.
• Prove Hybrid 1 = Hybrid 2 (and Hybrid 5 = Hybrid 4) by HCB security.
  The probability of $D$ distinguishing from Hybrid 1 and Hybrid 2 is determined by the advantage of computing the $HCB(r)$ from $F_i(r)$, which is negligible.
• Prove Hybrid 2 = Hybrid 3 ( and Hybrid 4 = Hybrid 3) by birthday paradox.
  The probability of $D$ distinguishing from Hybrid 0 and Hybrid 1 is up to the collision probability of $r$.
• QED.

Trapdoor Permutation Candidates

Trapdoor Permutations are exceedingly rare.

There are two candidates. (both need factoring to be hard)

• The RSA (Rivest-Shamir-Adleman) Function.
• The Rabin/Blum-Williams Function

This blog only show the RSA Trapdoor Permutation.

RSA Trapdoor Permutation

Let’s review some number theory from Lecture 6.

Let $N=pq$ be a product of two large primes.

Facts: $\mathbb{Z}_N^* =\{a\in \mathbb{Z}_N^*:\operatorname{gcd}(a,N)=1\}$ is a group.

• group operation is multiplication mod $N$.
• inverses exist and are easy to compute.
• the order of the group is $\phi(N)=(p-1)(q-1)$

Let $e$ be an integer with $\operatorname{gcd}(e,\phi(N))=1$.

Then, the map $F_{N,e}(x)=x^e\mod N$ is a trapdoor permutation.

The key fact is given $d$ such that $ed=1 \mod \phi(N)$, then it is easy to compute $x$ given $x^e$.

---

This gives us the RSA trapdoor permutation collection $\{F_{N,e}:\operatorname{gcd}(e,N)=1\}$.

• Function index is $(N,e)$
• Trapdoor for inversion is $d=e^{-1} \mod \phi(N)$

The hardness of inversion without trapdoor = RSA assumption:

Given $N,e$ (as above) and $x^e\mod N$, hard to compute $x$.